北京大学 wlw机器学习2022春季期末试题分析
北京大学 wlw机器学习2022春季期末试题分析
- 前言
- 新的开始
- 第一题
- 第二题
- 第三题
前言
你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。
新的开始
第一题

利用Lagrange Dueling,即可计算。
L ( x , λ 1 , λ 2 ) = b T x + λ 1 T ( c − A x ) − λ 2 T x ∂ L ∂ x = b T − λ 1 T A − λ 2 T = 0 L(x,\lambda_1,\lambda_2)=b^Tx+\lambda_1^T(c-Ax)-\lambda^T_2 x\\\frac{\partial L}{\partial x}=b^T-\lambda_1^TA-\lambda_2^T=0 L(x,λ1,λ2)=bTx+λ1T(c−Ax)−λ2Tx∂x∂L=bT−λ1TA−λ2T=0
故最终对偶形式为:
m a x λ 1 , λ 2 − λ 1 T c s . t . b T − λ 1 T A − λ 2 T = 0 λ 1 T ≥ 0 λ 2 T ≥ 0 max_{\lambda_1,\lambda_2}-\lambda_1^Tc\\ s.t. \quad b^T-\lambda_1^TA-\lambda_2^T=0\\ \lambda_1^T\geq0\\ \lambda_2^T\geq0 maxλ1,λ2−λ1Tcs.t.bT−λ1TA−λ2T=0λ1T≥0λ2T≥0
第二题

这里我个人认为要利用定义,还有就是要注意,这里提到的 c 1 c_1 c1, c 2 c_2 c2是存在,而不是任意。
L e t M d ( X , ϵ ) = m , ∃ x 1 , x 2 , . . . , x m ∈ X , ∀ i , j ∈ [ m ] , i ≠ j , d ( x i , x j ) ≥ ϵ G e t x m + 1 ∈ X , d ( x i , x m + 1 ) < ϵ S o c 2 ≥ 1 , N d ( X , ϵ / c 2 ) = M d ( X , ϵ / c 2 ) ≥ M d ( X , ϵ ) Let \quad\mathcal{M}_d(\mathcal{X}, \epsilon)=m,\\ \exist x_1,x_2,...,x_m\in\mathcal{X}, \forall i,j\in[m], i\neq j, d(x_i ,x_j)\geq \epsilon\\ Get\quad x_{m+1}\in\mathcal{X}, d(x_i,x_{m+1})<\epsilon\\ So \quad c_2\geq 1, \mathcal{N}_d(\mathcal{X},\epsilon/c_2)=\mathcal{M}_d(\mathcal{X},\epsilon/c_2)\geq \mathcal{M}_d(\mathcal{X},\epsilon) LetMd(X,ϵ)=m,∃x1,x2,...,xm∈X,∀i,j∈[m],i=j,d(xi,xj)≥ϵGetxm+1∈X,d(xi,xm+1)<ϵSoc2≥1,Nd(X,ϵ/c2)=Md(X,ϵ/c2)≥Md(X,ϵ)
对左半部分证明同理。
第三题

(1)思路,根据题目描述,要想证明两个分类器不同,由于不知道算法A,故只能通过比较误差进行,题目中提到了弱学习性假设,故考虑证明加权误差:
R ^ t + 1 ( h t ) = ∑ D t + 1 ( i ) I ( y i ≠ h t ( x i ) ) = ∑ D t ( i ) ∗ e x p ( − y i α t h t ( x i ) ) Z t I ( y i ≠ h t ( x i ) ) = ∑ D t ( i ) I ( y i ≠ h t ( x i ) ) e x p ( − y i α t h t ( x i ) ) Z t \hat{R}_{t+1}(h_t)=\sum D_{t+1}(i)I(y_i\neq h_t(x_i))\\ =\sum \frac{D_t(i)*exp(-y_i\alpha_t h_t(x_i))}{Z_t }I(y_i\neq h_t(x_i))\\ =\sum D_t(i)I(y_i\neq h_t(x_i))\frac{exp(-y_i\alpha_t h_t(x_i))}{Z_t } R^t+1(ht)=∑Dt+1(i)I(yi=ht(xi))=∑ZtDt(i)∗exp(−yiαtht(xi))I(yi=ht(xi))=∑Dt(i)I(yi=ht(xi))Ztexp(−yiαtht(xi))
相关文章:

北京大学 wlw机器学习2022春季期末试题分析
北京大学 wlw机器学习2022春季期末试题分析 前言新的开始第一题第二题第三题 前言 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。 新的开始 第…...
)
前端文件下载方法(包含get和post)
export const downloadFileWithIframe (url, name) > {const iframe document.createElement(iframe);iframe.style.display none; // 防止影响页面iframe.style.height 0; // 防止影响页面iframe.name name;iframe.src url;document.body.appendChild(iframe); // 这…...
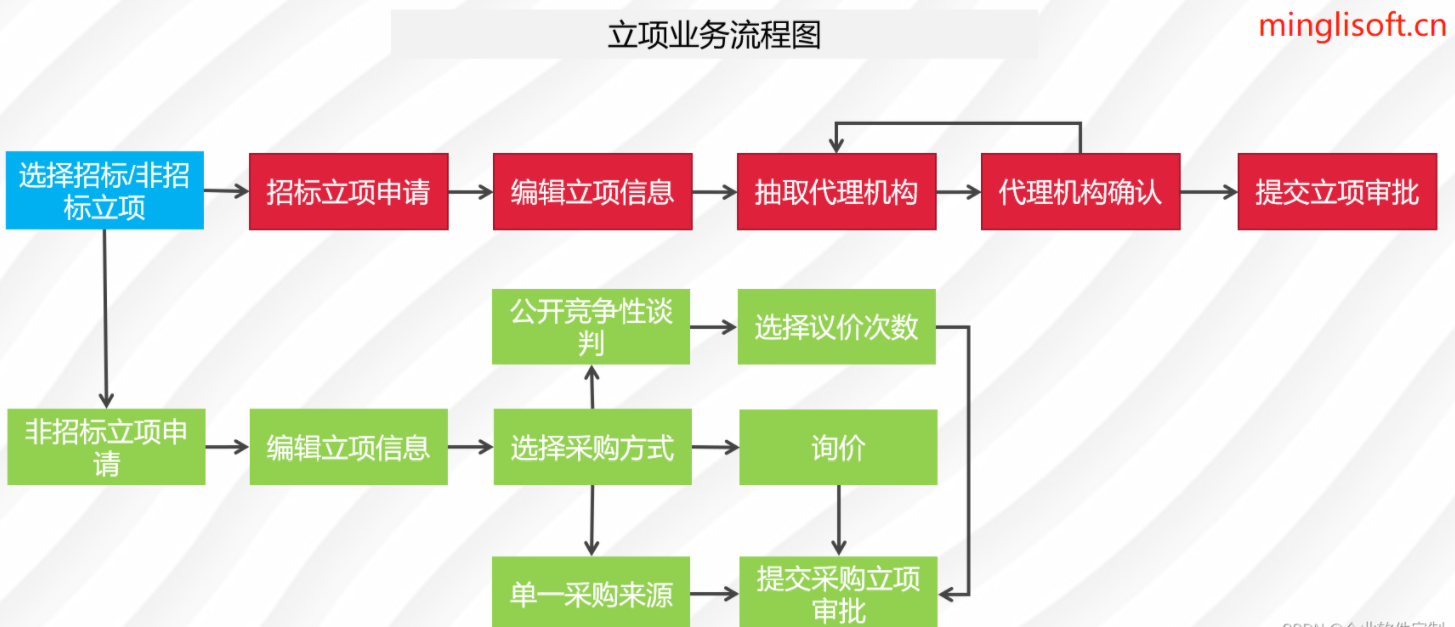
高性能、可扩展、支持二次开发的企业电子招标采购系统源码
在数字化时代,企业需要借助先进的数字化技术来提高工程管理效率和质量。招投标管理系统作为企业内部业务项目管理的重要应用平台,涵盖了门户管理、立项管理、采购项目管理、采购公告管理、考核管理、报表管理、评审管理、企业管理、采购管理和系统管理等…...

2645. 构造有效字符串的最少插入数
Problem: 2645. 构造有效字符串的最少插入数 文章目录 解题思路解决方法复杂度分析代码实现 解题思路 解决此问题需要确定如何以最小的插入次数构造一个有效的字符串。首先,我们需要确定开头的差距,然后决定中间的补足,最后决定末尾的差距。…...
C#,快速排序算法(Quick Sort)的非递归实现与数据可视化
排序算法是编程的基础。 常见的四种排序算法是:简单选择排序、冒泡排序、插入排序和快速排序。其中的快速排序的优势明显,一般使用递归方式实现,但遇到数据量大的情况则无法适用。实际工程中一般使用“非递归”方式实现。 快速排序(Quick Sor…...

【操作系统xv6】学习记录2 -RISC-V Architecture
说明:看完这节,不会让你称为汇编程序员,知识操作系统的前置。 ref:https://binhack.readthedocs.io/zh/latest/assembly/mips.html https://www.bilibili.com/video/BV1w94y1a7i8/?p7 MIPS MIPS的意思是 “无内部互锁流水级的微…...
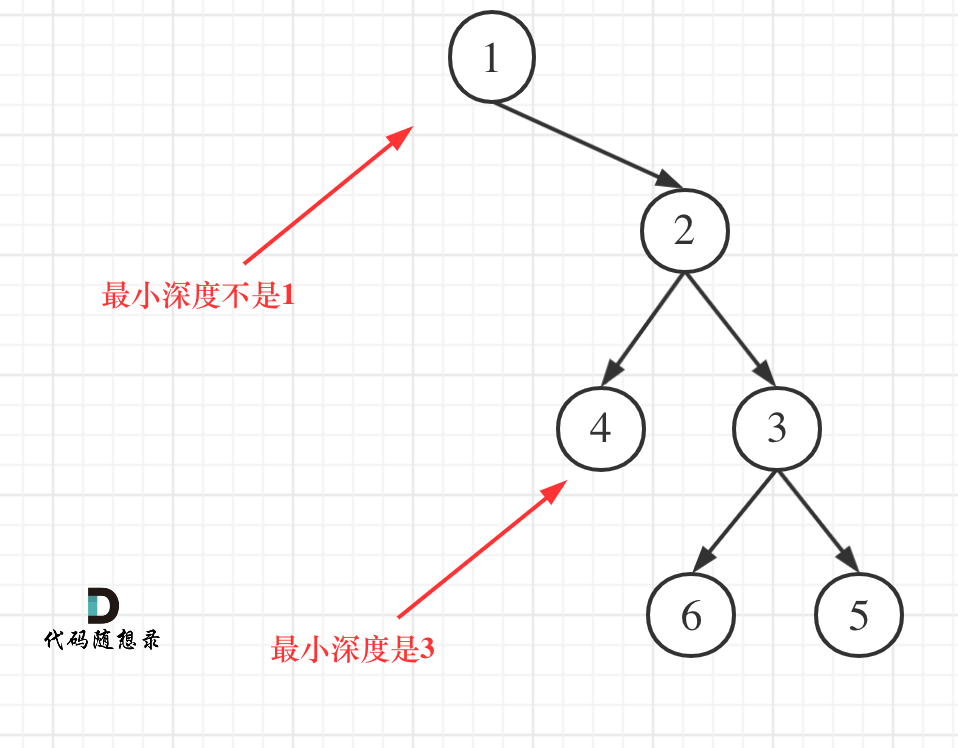
C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window) 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7], 返回它的最小深度 2 思路 看完了这篇104.二…...
)
【图像拼接】源码精读:Adaptive As-Natural-As-Possible Image Stitching(AANAP/ANAP)
第一次来请先看这篇文章:【图像拼接(Image Stitching)】关于【图像拼接论文源码精读】专栏的相关说明,包含专栏内文章结构说明、源码阅读顺序、培养代码能力、如何创新等(不定期更新) 【图像拼接论文源码精读】专栏文章目录 【源码精读】As-Projective-As-Possible Imag…...
解决docker run报错:Error response from daemon: No command specified.
将docker镜像export/import之后,对新的镜像执行docker run时报错: docker: Error response from daemon: No command specified. 解决方法: 方案1: 查看容器的command: docker ps --no-trunc 在docker run命令上增加…...

算法第十二天-最大整除子集
最大整除子集 题目要求 解题思路 来自[宫水三叶] 根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数 数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法…...

简单易懂的PyTorch 损失函数:优化机器学习模型的关键
目录 torch.nn子模块Loss Functions详解 nn.L1Loss 用途 用法 使用技巧 注意事项 代码示例 nn.MSELoss 用途 用法 使用技巧 注意事项 代码示例 nn.CrossEntropyLoss 用途 用法 使用技巧 注意事项 代码示例 使用类别索引 使用类别概率 nn.CTCLoss 用途 …...

Kubernetes/k8s的存储卷/数据卷
k8s的存储卷/数据卷 容器内的目录和宿主机的目录挂载 容器在系统上的生命周期是短暂的,delete,k8s用控制创建的pod,delete相当于重启,容器的状态也会回复到初始状态 一旦回到初始状态,所有的后天编辑的文件都会消失…...
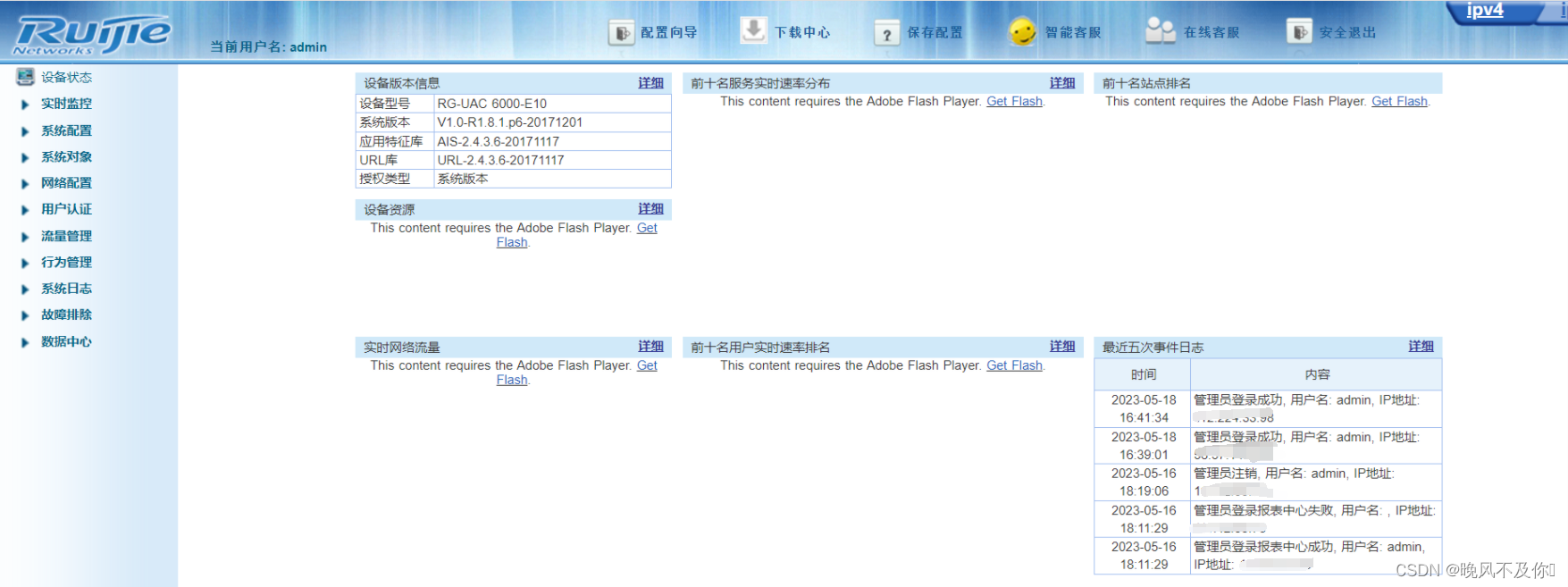
【漏洞复现】锐捷RG-UAC统一上网行为管理系统信息泄露漏洞
Nx01 产品简介 锐捷网络成立于2000年1月,原名实达网络,2003年更名,自成立以来,一直扎根行业,深入场景进行解决方案设计和创新,并利用云计算、SDN、移动互联、大数据、物联网、AI等新技术为各行业用户提供场…...
)
Android - 串口通讯(SerialPort)
最早的博客Android 模拟串口通信过程_launch virtual serial port driver pro-CSDN博客里就是用过 Google 提供的 demo,最近想再写个其他的demo发现用起来有点麻烦,还需要导入其他 module,因此在网上找到了Android-SerialPort-API: https://g…...

如何使用設置靜態住宅IP
靜態住宅IP就是一種靜態的、分配給住宅用戶的IP地址。與動態IP地址不同,靜態住宅IP一旦分配給用戶,就會一直保持不變,除非ISP(Internet Service Provider,互聯網服務提供商)進行手動更改。那麼,…...
在学习爬虫前的准备
1. 写一个爬虫程序需要分几步 获取网页内容。 我们会通过代码给一个网站服务器发送请求,它会返回给我们网页上的内容。 在我们平时使用浏览器访问服务器内容是,本质上也是向服务器发送一个请求,然后服务器返回网页上的内容。只不过浏览器还会…...
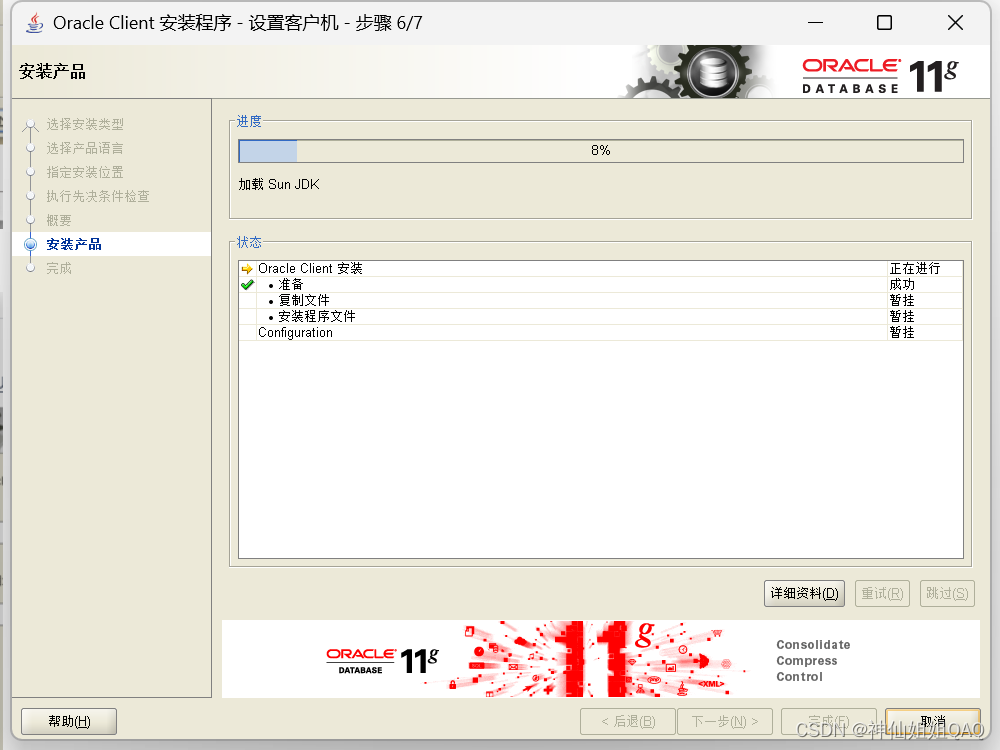
windows下安装oracle-win-64-11g超详细图文步骤
官方下载地址:点这里 1.根据自己电脑情况,解压64或者32位客户端,以及database压缩包 2.解压后双击执行database文件夹下的setup.exe 3.详细的安装步骤 (1)数据库安装 一、配置安全更新 电子邮件可写可不写…...

Go模板后端渲染时vue单页面冲突处理
go后端模版语法是通过 {{}} ,vue也是通过双花括号来渲染的,如果使用go渲染vue的html页面的时候就会报错,因为分别不出来哪个是vue的,哪个是go的,既可以修改go的模板语法 template.New("output").Delims(&qu…...

笔记本摄像头模拟监控推送RTSP流
使用笔记本摄像头模拟监控推送RTSP流 一、基础安装软件准备 本文使用软件下载链接:下载地址 FFmpeg软件: Download ffmpeg 选择Windows builds by BtbN 一个完整的跨平台解决方案,用于录制、转换和流式传输音频和视频。 EasyDarwin软件:Download Easy…...

鸿蒙开发已解决-ArkTS编译时遇到arkts-no-obj-literals-as-types错误
文章目录 项目场景:问题描述原因分析:解决方案:解决方案1解决方案2此Bug解决方案总结项目场景: 在开发鸿蒙项目过程中,遇到了arkts-no-obj-literals-as-types,总结了自己和网上人的解决方案,故写下这篇文章。 遇到问题: rkTS编译时遇到arkts-no-obj-literals-as-type…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
