[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记 - Ch02动态系统建模与分析
- 1. 课程介绍
- 2. 电路系统建模、基尔霍夫定律
- 3. 流体系统建模
- 4. 拉普拉斯变换(Laplace)传递函数、微分方程
- 4.1 Laplace Transform 拉式变换
- 4.2 收敛域(ROC)与逆变换(ILT)
- 4.3 传递函数 Transfer Function
- 5. 一阶系统的单位阶跃响应(step response),时间常数(Time Constant)
- 6. 频率响应与滤波器
- 7. 二阶系统
- 7.1 二阶系统对初始条件的动态响应 Matlab/Simulink - 2nd Order Syetem Response to IC
- 7.2 二阶系统的单位阶跃响应 2nd Order System Unit Step Response
- 7.3 二阶系统单位阶跃的性能分析与比较 2nd Order System Unit Step Response
- 7.4 共振现象-二阶系统频率响应,现象部分
- 7.5 二阶系统的频率响应
- 8. 二阶系统的频率响应
1. 课程介绍

2. 电路系统建模、基尔霍夫定律
基本元件:
电量 库伦( C C C) q q q
电流 安培( A A A) i i i —— i = d e d t i=\frac{\mathrm{d}e}{\mathrm{d}t} i=dtde 流速
电压 伏特( V V V) e e e
电阻 欧姆( Ω \varOmega Ω) R R R —— e R = i R e_{\mathrm{R}}=iR eR=iR
电容 法拉( F F F) C C C —— q = C e C , e C = 1 C q = 1 C ∫ 0 t i d t q=Ce_{\mathrm{C}},e_{\mathrm{C}}=\frac{1}{C}q=\frac{1}{C}\int_0^t{i}\mathrm{d}t q=CeC,eC=C1q=C1∫0tidt
电感 亨利( H H H) L L L —— e L = L d i d t = L i ′ e_{\mathrm{L}}=L\frac{\mathrm{d}i}{\mathrm{d}t}=Li^{\prime} eL=Ldtdi=Li′

基尔霍夫定律
K(Kirchhoff) C(Current) L(Law) —— 所有进入某节点的电流的总和等于所有离开这个节点的的电流总和
K(Kirchhoff) V(Voltage) L(Law) —— 沿着闭合回路所有元件两端的电压的代数和等于零

 )
)
3. 流体系统建模

流量 flow rate q q q m 3 / s m^3/s m3/s
体积 volume V V V m 3 m^3 m3
高度 heigh h h h m m m
压强 pressure p p p N / m ( p a s c a l ) N/m\left( pascal \right) N/m(pascal)
静压 Hydrostatic Pressure p H y d r o = F H y d r o A = m g A = ρ g h p_{\mathrm{Hydro}}=\frac{F_{\mathrm{Hydro}}}{A}=\frac{mg}{A}=\rho gh pHydro=AFHydro=Amg=ρgh
绝对压强 Asolute Pressure p a b s = p a + p H y d r o = p a + ρ g h p_{abs}=p_{\mathrm{a}}+p_{\mathrm{Hydro}}=p_{\mathrm{a}}+\rho gh pabs=pa+pHydro=pa+ρgh
表压 Gauge Pressure P g a u g e = p a b s − p a = ρ g h P_{\mathrm{gauge}}=p_{abs}-p_{\mathrm{a}}=\rho gh Pgauge=pabs−pa=ρgh
流阻 Fluid Resistance

质量守恒 Conservation of Mass

4. 拉普拉斯变换(Laplace)传递函数、微分方程
4.1 Laplace Transform 拉式变换
f ( t ) → F ( s ) f\left( t \right) \rightarrow F\left( s \right) f(t)→F(s) : 时域 - 频域 s = σ + j w s=\sigma +jw s=σ+jw





4.2 收敛域(ROC)与逆变换(ILT)


微分方程——描述动态世界
状态变量 : d x ⃗ d t \frac{\mathrm{d}\vec{x}}{\mathrm{d}t} dtdx-时间
位移: s s s , 速度: d x d t \frac{\mathrm{d}x}{\mathrm{d}t} dtdx ,加速度: d 2 x d t 2 \frac{\mathrm{d}^2x}{\mathrm{d}t^2} dt2d2x
- F = m d 2 x d t 2 F=m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} F=mdt2d2x
- d T d t = − k ( T − C ) \frac{\mathrm{d}T}{\mathrm{d}t}=-k\left( T-C \right) dtdT=−k(T−C)
- d P d t = − r p ( 1 − p k ) \frac{\mathrm{d}P}{\mathrm{d}t}=-rp\left( 1-\frac{p}{k} \right) dtdP=−rp(1−kp) 人口增长
常系数线性 —— 线性时不变系统
- 求解 3Step
从 t t t— s s s L [ f ( t ) ] \mathcal{L} \left[ f\left( t \right) \right] L[f(t)]
运算求解
从 s s s— t t t L − 1 [ F ( s ) ] \mathcal{L} ^{-1}\left[ F\left( s \right) \right] L−1[F(s)]
非线性
- 线性化
- 非线性分析控制

4.3 传递函数 Transfer Function
——根轨迹 BodePlot 信号处理


5. 一阶系统的单位阶跃响应(step response),时间常数(Time Constant)

换个角度分析单位阶跃响应(System Unit Step Response - 一阶 1st order)——LTI
一阶线性时不变 —— 1st order LTI
x ˙ + a x = a u x ( 0 ) = x ˙ ( 0 ) = 0 \dot{x}+ax=au \\ x\left( 0 \right) =\dot{x}\left( 0 \right) =0 x˙+ax=aux(0)=x˙(0)=0
传递函数 : s X ( s ) + a X ( s ) = a U ( s ) ; H ( s ) = X ( s ) U ( s ) = a s + a sX\left( s \right) +aX\left( s \right) =aU\left( s \right) ;H\left( s \right) =\frac{X\left( s \right)}{U\left( s \right)}=\frac{a}{s+a} sX(s)+aX(s)=aU(s);H(s)=U(s)X(s)=s+aa

Another Viewpoint : x ˙ + a x = a u , t ⩾ 0 , u = 1 ⇒ x ˙ = a − a x = a ( 1 − x ) \dot{x}+ax=au,t\geqslant 0,u=1\Rightarrow \dot{x}=a-ax=a\left( 1-x \right) x˙+ax=au,t⩾0,u=1⇒x˙=a−ax=a(1−x)

6. 频率响应与滤波器




1st order system 一阶系统

低通滤波器——Loss Pass Filter

7. 二阶系统
7.1 二阶系统对初始条件的动态响应 Matlab/Simulink - 2nd Order Syetem Response to IC
Vibration 振动



7.2 二阶系统的单位阶跃响应 2nd Order System Unit Step Response

Unit Step Imput 单位阶跃


7.3 二阶系统单位阶跃的性能分析与比较 2nd Order System Unit Step Response


7.4 共振现象-二阶系统频率响应,现象部分

7.5 二阶系统的频率响应

8. 二阶系统的频率响应

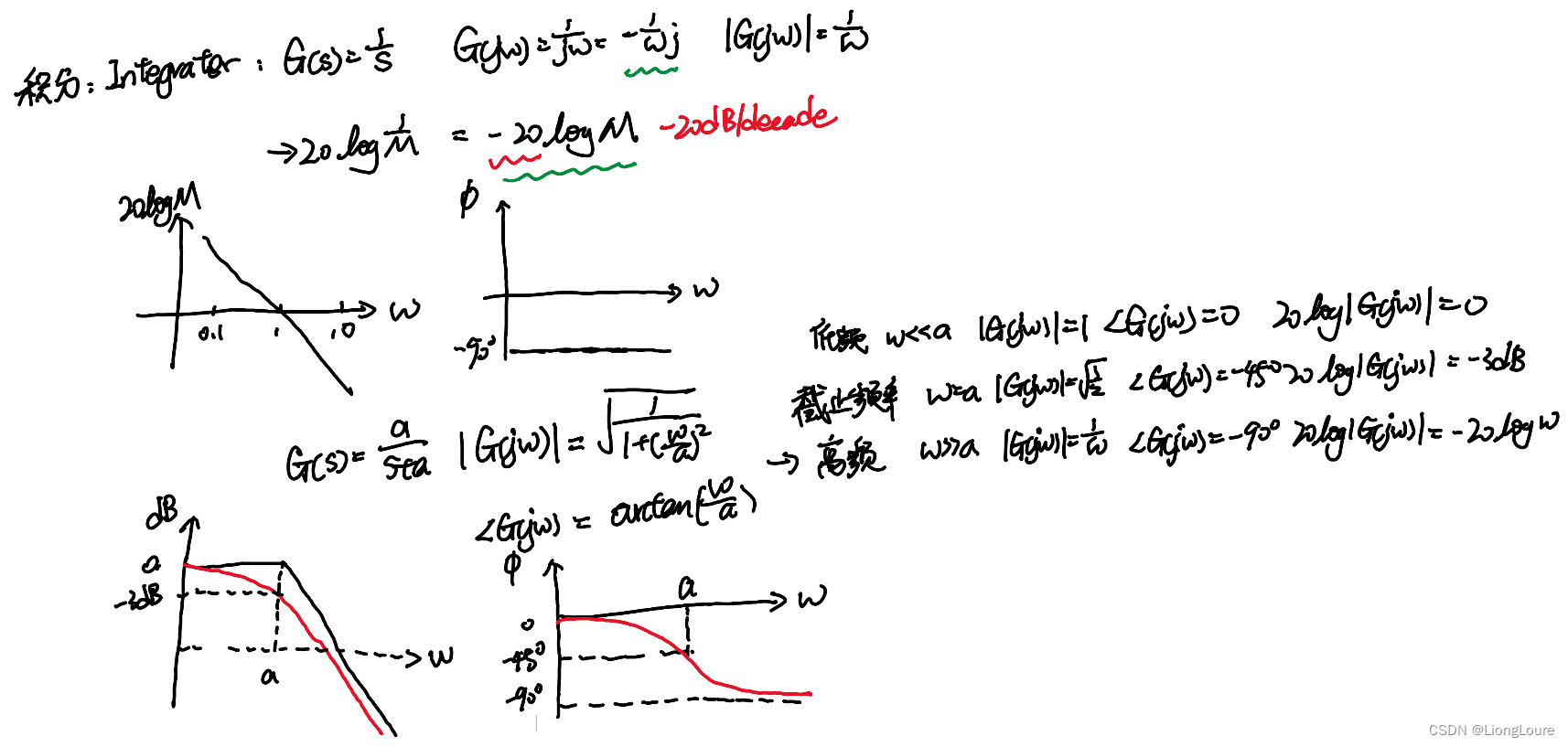
Bode Plot 手绘技巧与应用


相关文章:

[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记 - Ch02动态系统建模与分析 1. 课程介绍2. 电路系统建模、基尔霍夫定律3. 流体系统建模4. 拉普拉斯变换(Laplace)传递函数、微分方程4.1 Laplace Transform 拉式变换4.2 收…...

【一周年创作总结】人生是远方的无尽旷野呀
那一眼瞥见的伟大的灵魂,却似模糊的你和我 文章目录 📒各个阶段的experience🔎大一寒假🔎大一下学期🔎大一暑假🔎大二上学期(现在) 🍔相遇CSDN🛸自媒体&#…...

金融帝国实验室(Capitalism Lab)V10版本游戏平衡性优化与改进
即将推出的V10版本中的各种游戏平衡性优化与改进: ————————————— 一、当玩家被提议收购一家即将破产的公司时,显示商业秘密。 当一家公司濒临破产,玩家被提议收购该公司时,如果玩家有兴趣评估该公司,则无…...

[SpringBoot]接口的多实现:选择性注入SpringBoot接口的实现类
最近在项目中遇到两种情况,准备写个博客记录一下。 情况说明:Service层一个接口是否可以存在多个具体实现,此时应该如何调用Service(的具体实现)? 其实之前的项目中也遇到过这种情况,只不过我采…...

北京大学 wlw机器学习2022春季期末试题分析
北京大学 wlw机器学习2022春季期末试题分析 前言新的开始第一题第二题第三题 前言 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。 新的开始 第…...
)
前端文件下载方法(包含get和post)
export const downloadFileWithIframe (url, name) > {const iframe document.createElement(iframe);iframe.style.display none; // 防止影响页面iframe.style.height 0; // 防止影响页面iframe.name name;iframe.src url;document.body.appendChild(iframe); // 这…...
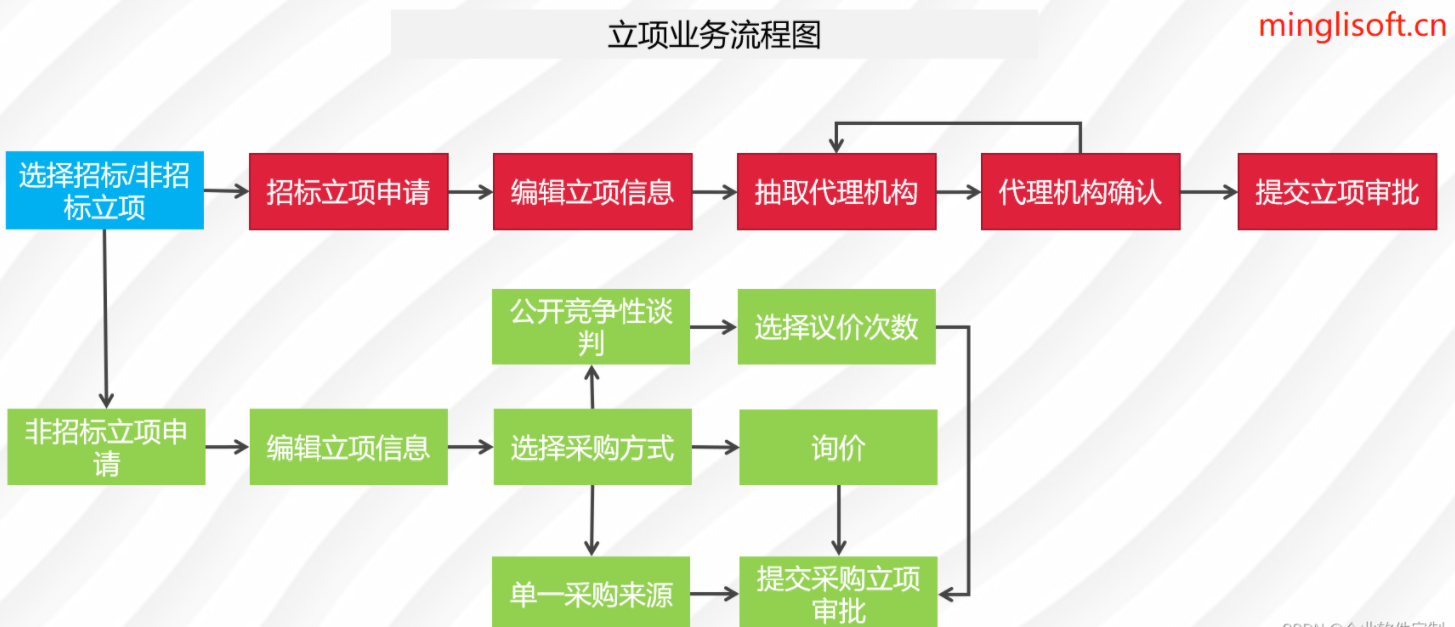
高性能、可扩展、支持二次开发的企业电子招标采购系统源码
在数字化时代,企业需要借助先进的数字化技术来提高工程管理效率和质量。招投标管理系统作为企业内部业务项目管理的重要应用平台,涵盖了门户管理、立项管理、采购项目管理、采购公告管理、考核管理、报表管理、评审管理、企业管理、采购管理和系统管理等…...

2645. 构造有效字符串的最少插入数
Problem: 2645. 构造有效字符串的最少插入数 文章目录 解题思路解决方法复杂度分析代码实现 解题思路 解决此问题需要确定如何以最小的插入次数构造一个有效的字符串。首先,我们需要确定开头的差距,然后决定中间的补足,最后决定末尾的差距。…...
C#,快速排序算法(Quick Sort)的非递归实现与数据可视化
排序算法是编程的基础。 常见的四种排序算法是:简单选择排序、冒泡排序、插入排序和快速排序。其中的快速排序的优势明显,一般使用递归方式实现,但遇到数据量大的情况则无法适用。实际工程中一般使用“非递归”方式实现。 快速排序(Quick Sor…...

【操作系统xv6】学习记录2 -RISC-V Architecture
说明:看完这节,不会让你称为汇编程序员,知识操作系统的前置。 ref:https://binhack.readthedocs.io/zh/latest/assembly/mips.html https://www.bilibili.com/video/BV1w94y1a7i8/?p7 MIPS MIPS的意思是 “无内部互锁流水级的微…...
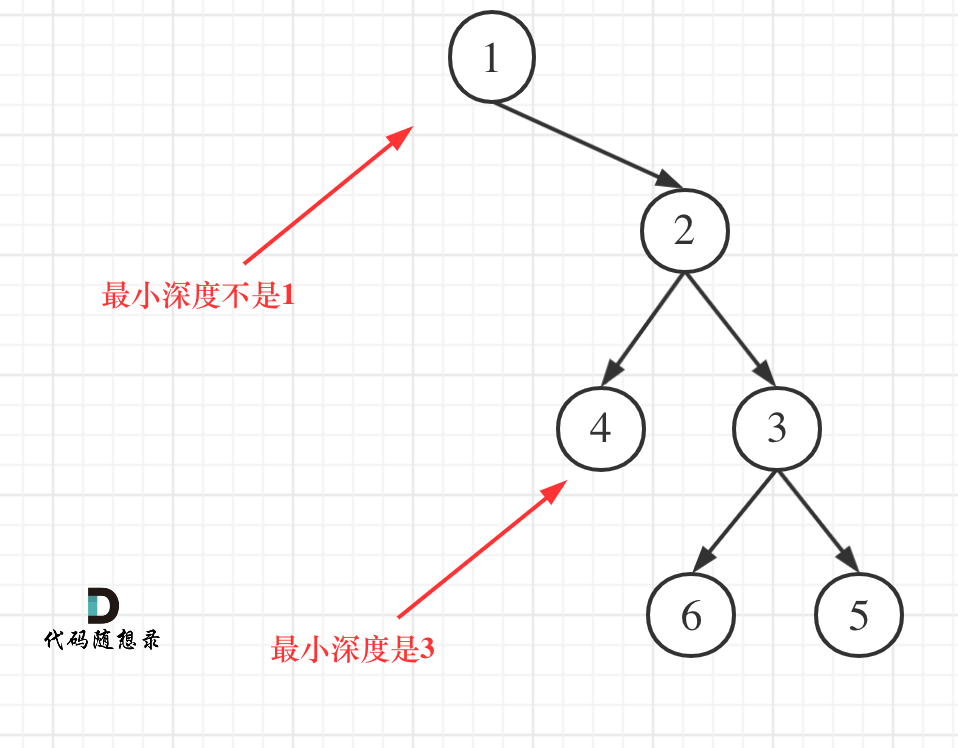
C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window) 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7], 返回它的最小深度 2 思路 看完了这篇104.二…...
)
【图像拼接】源码精读:Adaptive As-Natural-As-Possible Image Stitching(AANAP/ANAP)
第一次来请先看这篇文章:【图像拼接(Image Stitching)】关于【图像拼接论文源码精读】专栏的相关说明,包含专栏内文章结构说明、源码阅读顺序、培养代码能力、如何创新等(不定期更新) 【图像拼接论文源码精读】专栏文章目录 【源码精读】As-Projective-As-Possible Imag…...
解决docker run报错:Error response from daemon: No command specified.
将docker镜像export/import之后,对新的镜像执行docker run时报错: docker: Error response from daemon: No command specified. 解决方法: 方案1: 查看容器的command: docker ps --no-trunc 在docker run命令上增加…...

算法第十二天-最大整除子集
最大整除子集 题目要求 解题思路 来自[宫水三叶] 根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数 数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法…...

简单易懂的PyTorch 损失函数:优化机器学习模型的关键
目录 torch.nn子模块Loss Functions详解 nn.L1Loss 用途 用法 使用技巧 注意事项 代码示例 nn.MSELoss 用途 用法 使用技巧 注意事项 代码示例 nn.CrossEntropyLoss 用途 用法 使用技巧 注意事项 代码示例 使用类别索引 使用类别概率 nn.CTCLoss 用途 …...

Kubernetes/k8s的存储卷/数据卷
k8s的存储卷/数据卷 容器内的目录和宿主机的目录挂载 容器在系统上的生命周期是短暂的,delete,k8s用控制创建的pod,delete相当于重启,容器的状态也会回复到初始状态 一旦回到初始状态,所有的后天编辑的文件都会消失…...
【漏洞复现】锐捷RG-UAC统一上网行为管理系统信息泄露漏洞
Nx01 产品简介 锐捷网络成立于2000年1月,原名实达网络,2003年更名,自成立以来,一直扎根行业,深入场景进行解决方案设计和创新,并利用云计算、SDN、移动互联、大数据、物联网、AI等新技术为各行业用户提供场…...
)
Android - 串口通讯(SerialPort)
最早的博客Android 模拟串口通信过程_launch virtual serial port driver pro-CSDN博客里就是用过 Google 提供的 demo,最近想再写个其他的demo发现用起来有点麻烦,还需要导入其他 module,因此在网上找到了Android-SerialPort-API: https://g…...

如何使用設置靜態住宅IP
靜態住宅IP就是一種靜態的、分配給住宅用戶的IP地址。與動態IP地址不同,靜態住宅IP一旦分配給用戶,就會一直保持不變,除非ISP(Internet Service Provider,互聯網服務提供商)進行手動更改。那麼,…...
在学习爬虫前的准备
1. 写一个爬虫程序需要分几步 获取网页内容。 我们会通过代码给一个网站服务器发送请求,它会返回给我们网页上的内容。 在我们平时使用浏览器访问服务器内容是,本质上也是向服务器发送一个请求,然后服务器返回网页上的内容。只不过浏览器还会…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
