数据结构学习笔记——查找算法中的树形查找(红黑树)
目录
- 一、红黑树的定义
- (一)黑/红结点、叶子节点
- (二)黑色完美平衡
- 二、红黑树的性质
- (一)黑高和高度
- (二)叶子结点个数
- 三、红黑树与AVL对比
一、红黑树的定义
红黑树是一棵二叉排序树(满足结点值中:左子树<根结点<右子树),每个结点都带有颜色属性,即黑或红。可以简单地说它是一棵“ 平衡二叉树 ”,但由于它的左、右子树高度差的绝对值有可能超过 1,所以并不是严格意义上的平衡二叉树,只能说是一棵弱平衡二叉树,相对于正常的平衡二叉树,在进行插入、删除操作后二叉树的平衡调整中由于不要求完全平衡,其所需的代价更低。
(一)黑/红结点、叶子节点
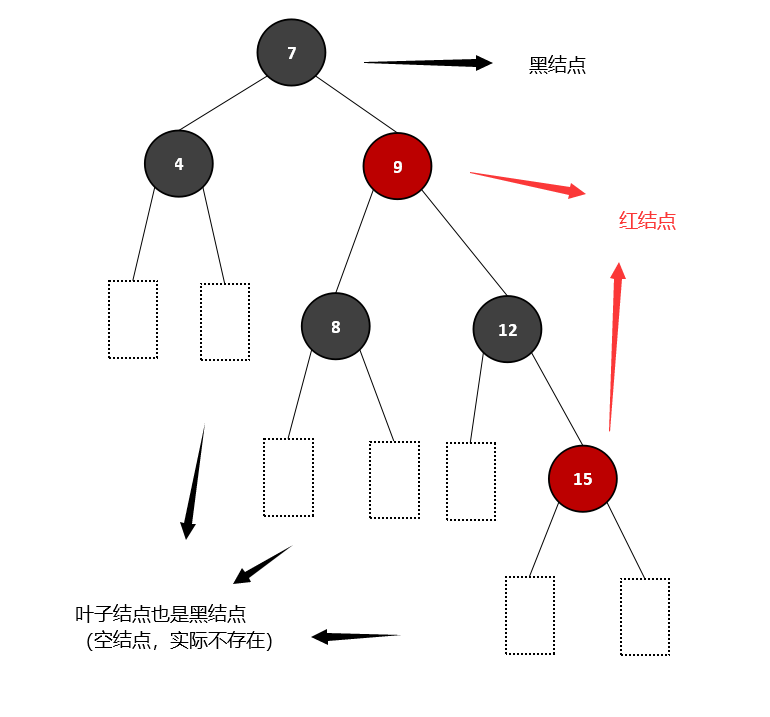
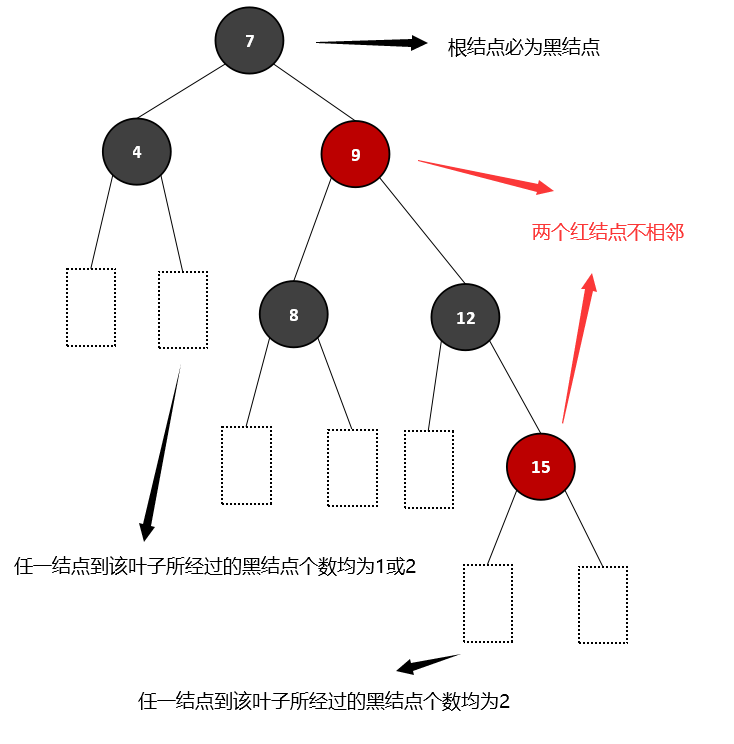
在红黑树中,根结点一定是黑结点,其余结点为黑或红,树中不允许有相邻的两个红结点;另外,树中也存在叶子结点,它是黑结点,是实际意义上不存在的空结点,且任一结点(不包括)到叶子结点的路径上,所经过的黑结点的个数相同,注意叶子结点也算作黑结点计入。
(二)黑色完美平衡
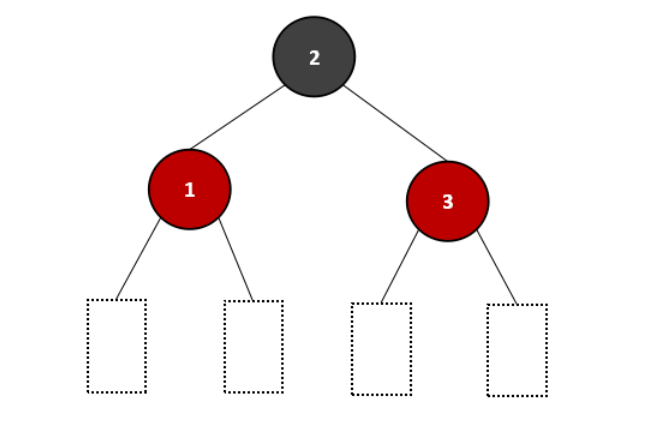
若红黑树中,左子树和右子树的层数相等,则称为黑色完美平衡,如下:
二、红黑树的性质
(一)黑高和高度
任意一结点(不包括)到叶子结点所经过的黑结点的个数称为该结点的黑高,而根结点的黑高即为红黑树的高度,黑高用bh表示,例如,下图这棵红黑树的高度即为根结点3的黑高,即bh=2:
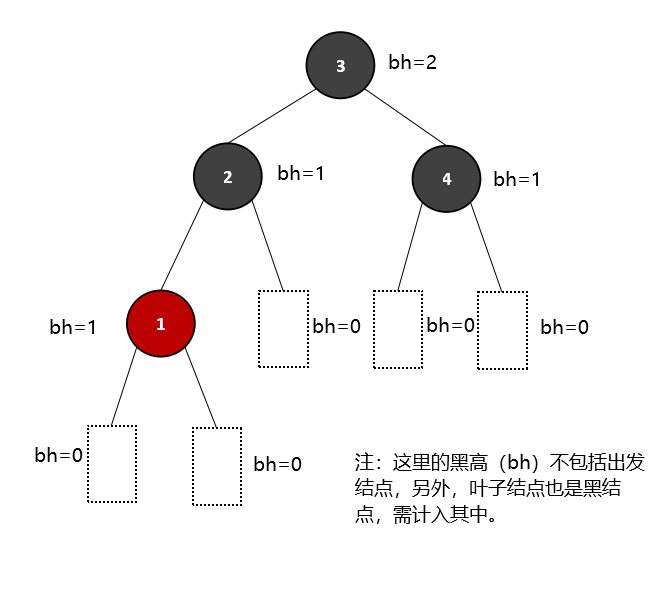
由于根结点到叶子结点的最长路径不大于最短路径的两倍,且至少有一半结点为黑结点,即树的黑高至少为h/2,所以对于一个含有n个结点的红黑树,其高度为h ≤ 2log2(n+1),即最大高度为2log2(n+1)。
(二)叶子结点个数
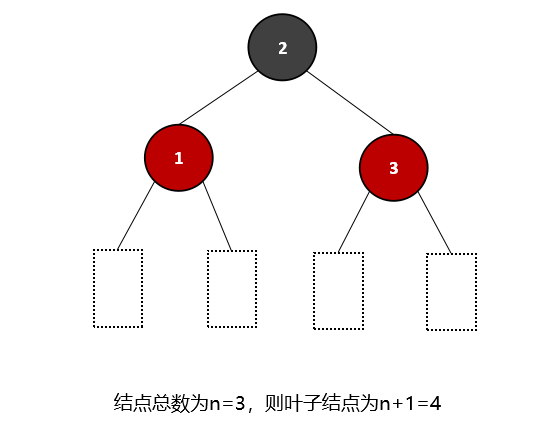
红黑树中,叶子结点(空结点)与二分判定树和B树中的外部结点相同,都不是实际存在的结点,是虚构的。若红黑树的结点总数为n,则外部结点的个数为n+1。
三、红黑树与AVL对比
与平衡二叉树(AVL)相比,红黑树只追求大致上的平衡,通过引入红、黑颜色属性以及相应的规则来保证平衡性,所以红黑树在插入和删除结点时只需进行少量的颜色调整和旋转操作,从而比AVL实现更简便,而AVL必须遵从严格的平衡条件,使得在进行插入和删除结点操作后需要多次旋转调整来保证平衡,可能会增加操作的时间复杂度。另外,AVL与红黑树相同,两者查找、插入和删除操作的时间复杂度均为O(log2n)。
由于每一棵红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
相关文章:

数据结构学习笔记——查找算法中的树形查找(红黑树)
目录 一、红黑树的定义(一)黑/红结点、叶子节点(二)黑色完美平衡 二、红黑树的性质(一)黑高和高度(二)叶子结点个数 三、红黑树与AVL对比 一、红黑树的定义 红黑树是一棵二叉排序树…...

Debezium发布历史66
原文地址: https://debezium.io/blog/2019/07/25/debezium-0-10-0-beta3-released/ 欢迎关注留言,我是收集整理小能手,工具翻译,仅供参考,笔芯笔芯. Debezium 0.10.0.Beta3 发布 七月 25, 2019 作者: Jir…...

Redis系列之使用Lua脚本
什么是lua脚本? lua语言是一个轻量级的脚本语言,可以嵌入其他语言中使用,调用宿主语言的功能。lua语法简单,小巧,源码一共才200多K,本身不会有太强的功能,很多的语言也支持lua语言,…...

Wargames与bash知识16
Wargames与bash知识16 Bandit24 关卡提示: 一个守护进程正在端口30002上侦听,如果给定bandit24的密码和一个4位数的密码,它将为您提供bandit25的密码。没有办法检索pincode,除非遍历所有10000个组合,称为暴力强制。您…...

关于运维·关于数据库面试题
目录 一、数据库类型 二、数据库引擎 三、mysql数据库类型 四、mysql的约束添加 五、主从复制原理 六、主从方式有几种 七、mysql主从数据不一致的原因 八、mysql的优化 九、什么是事务的特征 十、数据库读写分离的好处 十一、怎样优化sql语句 十二、mysql的同步方…...
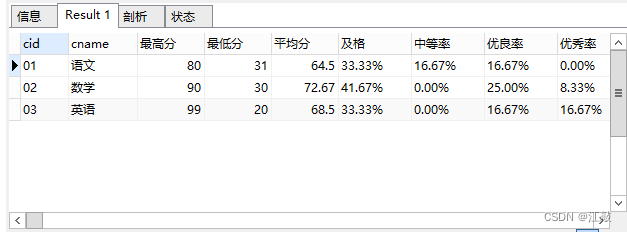
MySQL题目示例
文章目录 1.题目示例 1.题目示例 09)查询学过「张三」老师授课的同学的信息 SELECT s.*, c.cname, t.tname, sc.score FROM t_mysql_teacher t, t_mysql_course c, t_mysql_student s, t_mysql_score sc WHERE t.tid c.tid AND c.cid sc.cid AND sc.sid s.sid …...

HTML基本语法
HTML基本语法 1.介绍: 1.1超文本: 指的是网页中可以显示的内容(图片,超链接,视频…) 1.2标记:标签(通过标记符号来告诉浏览器网页内容该如何显示) 标记语言中,提供了许多的标签,不同的标签…...
二分图最大匹配——匈牙利算法详解
文章目录 零、前言一、红娘牵线二、二分图最大匹配2.1概念2.2交替路2.3增广路2.4匈牙利算法2.4.1算法原理2.4.2算法示例2.4.3代码实现 3.OJ练习3.1模板3.2棋盘覆盖3.3車的放置 零、前言 关于二分图的基本知识见:二分图及染色法判定 一、红娘牵线 一位红娘近日遇到一…...

【AI视野·今日Robot 机器人论文速览 第七十一期】Fri, 5 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Fri, 5 Jan 2024 Totally 11 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Machine Learning in Robotic Ultrasound Imaging: Challenges and Perspectives Authors Yuan Bi, Zhongliang Jiang, Felix D…...

xtu oj 1334 Least Common Multiple
题目描述 一个集合,任取3个不同的元素,求其最小公倍数中最小的值是多少? 输入 第一行是样例数T(1≤T≤100)。 每个样例的第一行是一个整数n(3≤n≤50),表示集合元素的个数。 每个样例的第二行是n个整数a1,a2,…,an,1≤ai≤106。…...
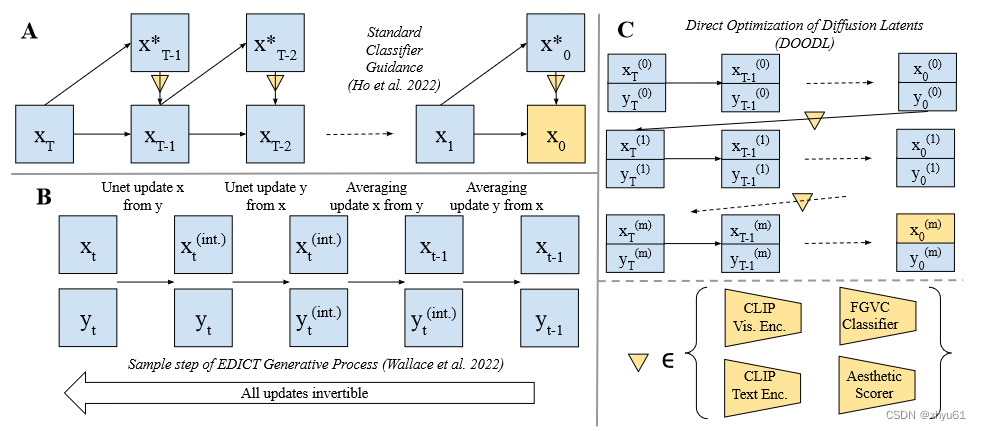
【论文笔记】End-to-End Diffusion Latent Optimization Improves Classifier Guidance
Abstract Classifier guidance为图像生成带来了控制,但是需要训练新的噪声感知模型(noise-aware models)来获得准确的梯度,或使用最终生成的一步去噪近似,这会导致梯度错位(misaligned gradients)和次优控制(sub-optimal control)。 梯度错位…...
【HarmonyOS4.0】第四篇-ArkUI基础实战
一、ArkUI框架简介 ArkUI开发框架是方舟开发框架的简称,它是一套构建 HarmonyOS / OpenHarmony 应用界面的声明式UI开发框架,它使用极简的UI信息语法、丰富的UI组件以及实时界面语言工具,帮助开发者提升应用界面开发效率 30%,开发…...

每日一题——LeetCode1128.等价多米诺骨牌对的数量
先尝试暴力解法: var numEquivDominoPairs function(dominoes) {var count0for(let i0;i<dominoes.length-1;i){for(let ji1;j<dominoes.length;j){if((dominoes[i][0]dominoes[j][0] && dominoes[i][1]dominoes[j][1]) || (dominoes[i][0]dominoes…...
关联规则分析(Apriori算法2
目录 1.核心术语:2.强关联规则:小结: 1.核心术语: 支持度(Support):指项集出现的频繁程度(相当于项集出现的概率) 最小支持度有绝对值和占比两种表示方式 置信度&#…...
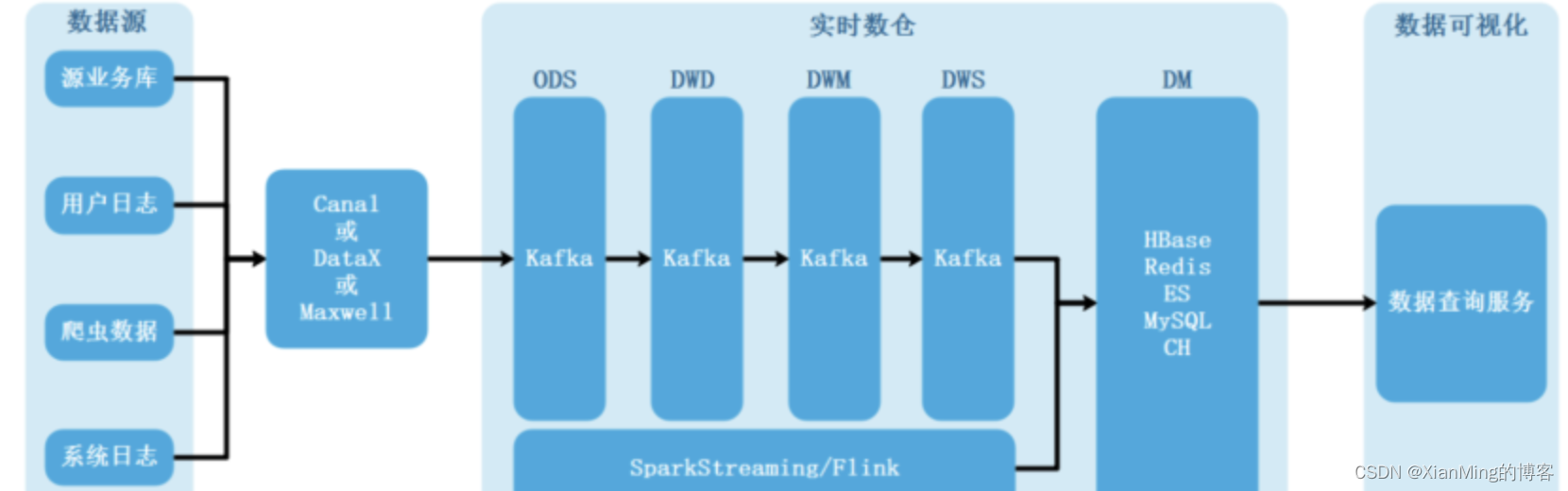
数据仓库(2)-认识数仓
1、数据仓库是什么 数据仓库 ,由数据仓库之父比尔恩门(Bill Inmon)于1990年提出,主要功能仍是将组织透过资讯系统之联机事务处理(OLTP)经年累月所累积的大量资料,透过数据仓库理论所特有的资料储存架构,做…...

C#编程-实现委托
实现委托 委托是可以存储对方法的引用的对象。在C#中,委托允许您动态地改变类中方法的引用。 考虑咖啡售货机的示例,它配置不同口味的咖啡,例如卡布奇诺咖啡和黑咖啡。在选择所需口味的咖啡时,售货机决定混合各种成分,例如奶粉、咖啡粉、热水、卡布奇诺咖啡粉。所有的材…...
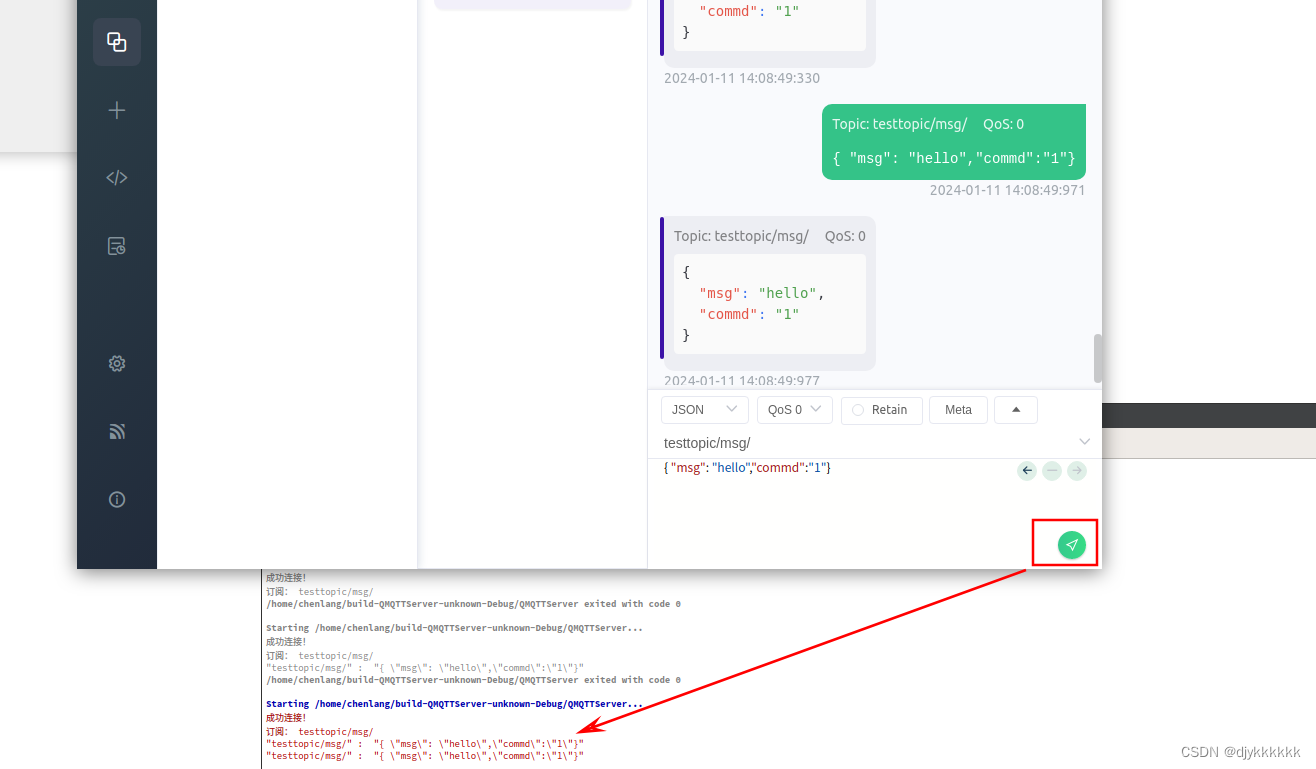
Ubuntu18.04 Qt 实现MQTT
什么是MQTT? 作用是什么(适用场景)? 与其他通讯协议相比,优缺点在那里? 一.安装 MQTT 服务器 使用 EMQ X(开源且可视化管理) 下载 EMQX 下载的是 emqx-5.0.26-ubuntu18.04-…...

【软件测试】学习笔记-不同视角的软件性能与性能指标
本篇文章探讨新的测试主题:性能测试,因为性能测试的专业性很强,所以我会以从0到1的入门者视角,系统性地阐述性能测试的方法以及应用领域,用实例去诠释各种性能指标。 本篇文章站在全局的视角,帮你梳理软件性…...
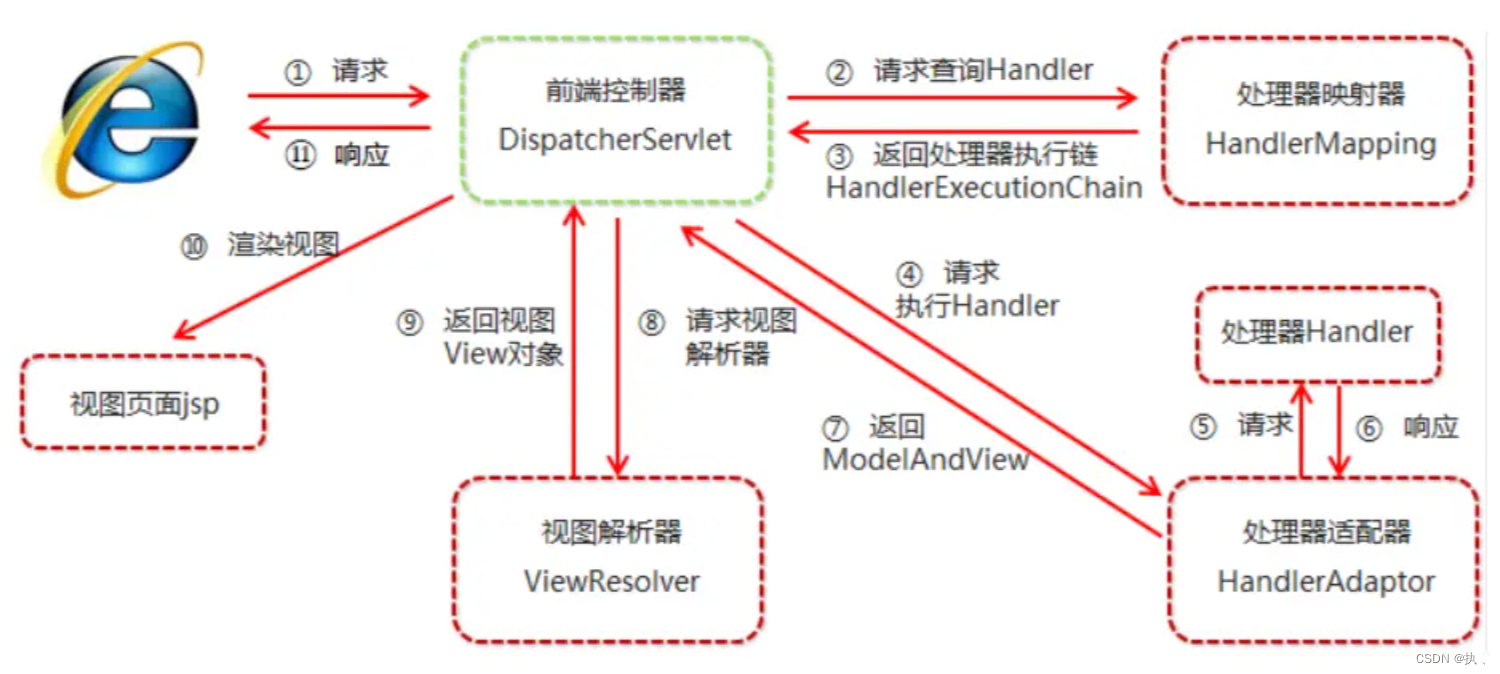
Spring MVC组件
1.DispatcherServlet前端控制器 用户请求到达前端控制器,它就相当于mvc模式中的c,dispatcherServlet 是整个流程控制的中心,由它调用其它组件处理用户的请求,dispatcherServlet 的存在降低了组件之间的耦合性。 2.HandlerMappin…...

vue文件在<template>中使用多个<el-main>报错(已解决)
目录 1.原理 2. 根据你的需求,自定义每个 组件的内容。你可以在 标签内部插入文本、其他组件、样式等。 3. 根据需要添加样式或其他属性到每个 组件。你可以使用 class、style 或其他属性来自定义每个组件的外观和行为。 4.一个可以运行的总代码如下 5.我的一…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
