CF1446B Catching Cheaters 题解 DP
Catching Cheaters
传送门
题面翻译
给我们两个字符串,让我们从中选出两个字串,算出它们的最大公共子序列长度。然后将它乘 4 4 4在减去两个字串的长度。问你这个数最大是多少。
题目描述
You are given two strings A A A and B B B representing essays of two students who are suspected cheaters. For any two strings C C C , D D D we define their similarity score S ( C , D ) S(C,D) S(C,D) as 4 ⋅ L C S ( C , D ) − ∣ C ∣ − ∣ D ∣ 4\cdot LCS(C,D) - |C| - |D| 4⋅LCS(C,D)−∣C∣−∣D∣ , where L C S ( C , D ) LCS(C,D) LCS(C,D) denotes the length of the Longest Common Subsequence of strings C C C and D D D .
You believe that only some part of the essays could have been copied, therefore you’re interested in their substrings.
Calculate the maximal similarity score over all pairs of substrings. More formally, output maximal S ( C , D ) S(C, D) S(C,D) over all pairs ( C , D ) (C, D) (C,D) , where C C C is some substring of A A A , and $ D $ is some substring of B B B .
If X X X is a string, ∣ X ∣ |X| ∣X∣ denotes its length.
A string a a a is a substring of a string b b b if a a a can be obtained from b b b by deletion of several (possibly, zero or all) characters from the beginning and several (possibly, zero or all) characters from the end.
A string a a a is a subsequence of a string b b b if a a a can be obtained from b b b by deletion of several (possibly, zero or all) characters.
Pay attention to the difference between the substring and subsequence, as they both appear in the problem statement.
You may wish to read the Wikipedia page about the Longest Common Subsequence problem.
输入格式
The first line contains two positive integers n n n and m m m ( 1 ≤ n , m ≤ 5000 1 \leq n, m \leq 5000 1≤n,m≤5000 ) — lengths of the two strings A A A and B B B .
The second line contains a string consisting of n n n lowercase Latin letters — string A A A .
The third line contains a string consisting of m m m lowercase Latin letters — string B B B .
输出格式
Output maximal S ( C , D ) S(C, D) S(C,D) over all pairs ( C , D ) (C, D) (C,D) , where C C C is some substring of A A A , and D D D is some substring of B B B .
样例 #1
样例输入 #1
4 5
abba
babab
样例输出 #1
5
样例 #2
样例输入 #2
8 10
bbbbabab
bbbabaaaaa
样例输出 #2
12
样例 #3
样例输入 #3
7 7
uiibwws
qhtkxcn
样例输出 #3
0
提示
For the first case:
abb from the first string and abab from the second string have LCS equal to abb.
The result is S ( a b b , a b a b ) = ( 4 ⋅ ∣ a b b ∣ ) − ∣ a b b ∣ − ∣ a b a b ∣ = 4 ⋅ 3 − 3 − 4 = 5 S(abb, abab) = (4 \cdot |abb|) - |abb| - |abab| = 4 \cdot 3 - 3 - 4 = 5 S(abb,abab)=(4⋅∣abb∣)−∣abb∣−∣abab∣=4⋅3−3−4=5 .
以上来自洛谷 以上来自洛谷 以上来自洛谷
解题思路
首先,暴力肯定过不了。
考虑DP。设 f i , j f_{i,j} fi,j 表示以 a i , b i a_i,b_i ai,bi 为两字串的末位的相似值(相似值计算: 4 × L C S ( A , B ) − ∣ A ∣ − ∣ B ∣ 4 \times LCS(A,B)-|A|-|B| 4×LCS(A,B)−∣A∣−∣B∣)。当 i + 1 i+1 i+1 或 j + 1 j+1 j+1 时,对 L C S ( A , B ) LCS(A,B) LCS(A,B) 无贡献,而对 ∣ A ∣ |A| ∣A∣ 或 ∣ B ∣ |B| ∣B∣ 贡献为 1 1 1,所以对相似值贡献为 ( 4 × L C S ( A ′ , B ) − ∣ A ′ ∣ − ∣ B ∣ ) − ( 4 × L C S ( ∣ A ∣ , ∣ B ∣ ) − ∣ A ∣ − ∣ B ∣ ) = ( 4 × L C S ( A , B ) − ( ∣ A ∣ + 1 ) − ∣ B ∣ ) − ( 4 × L C S ( A , B ) − ∣ A ∣ − ∣ ∣ B ) = 4 ∗ L C S ( A , B ) − ∣ A ∣ − 1 − ∣ B ∣ − 4 × L C S ( A , B ) + ∣ A ∣ + ∣ B ∣ = − 1 (4\times LCS(A',B)-|A'|-|B|)-(4\times LCS(|A|,|B|)-|A|-|B|)=(4\times LCS(A,B)-(|A|+1)-|B|)-(4\times LCS(A,B)-|A|-||B)=4*LCS(A,B)-|A|-1-|B|-4\times LCS(A,B)+|A|+|B|=-1 (4×LCS(A′,B)−∣A′∣−∣B∣)−(4×LCS(∣A∣,∣B∣)−∣A∣−∣B∣)=(4×LCS(A,B)−(∣A∣+1)−∣B∣)−(4×LCS(A,B)−∣A∣−∣∣B)=4∗LCS(A,B)−∣A∣−1−∣B∣−4×LCS(A,B)+∣A∣+∣B∣=−1,则有 f i , j = max ( f i , j , max ( f i − 1 , j , f i , j − 1 ) ) f_{i,j}=\max(f_{i,j},\max(f_{i-1,j},f_{i,j-1})) fi,j=max(fi,j,max(fi−1,j,fi,j−1))。当 i + 1 i+1 i+1 且 j + 1 j+1 j+1 的同时满足 a i + 1 = b j + 1 a_{i+1}=b_{j+1} ai+1=bj+1,则对 L C S ( A , B ) LCS(A,B) LCS(A,B) 的贡献为 4 4 4,对 ∣ A ∣ + ∣ B ∣ |A|+|B| ∣A∣+∣B∣ 的贡献为 2 2 2,所以对相似值的贡献为 ( 4 × L C S ( A ′ , B ′ ) − ∣ A ′ ∣ − ∣ B ′ ∣ ) − ( 4 × L C S ( A , B ) − ∣ A ∣ − ∣ B ∣ ) = ( 4 × ( L C S ( A , B ) + 1 ) − ( ∣ A ∣ + 1 ) − ( ∣ B ∣ + 1 ) ) − ( 4 × L C S ( A , B ) − ∣ A ∣ − ∣ B ∣ ) = ( 4 × L C S ( A , B ) + 4 − ∣ A ∣ − 1 − ∣ B ∣ − 1 ) − ( 4 × L C S ( A , B ) − ∣ A ∣ − ∣ B ∣ ) = 4 × L C S ( A , B ) + 4 − ∣ A ∣ − 1 − ∣ B ∣ − 1 − 4 × L C S ( A , B ) + ∣ A ∣ + ∣ B ∣ = 2 (4\times LCS(A',B')-|A'|-|B'|)-(4\times LCS(A,B)-|A|-|B|)=(4\times (LCS(A,B)+1)-(|A|+1)-(|B|+1))-(4\times LCS(A,B)-|A|-|B|)=(4\times LCS(A,B)+4-|A|-1-|B|-1)-(4\times LCS(A,B)-|A|-|B|)=4\times LCS(A,B)+4-|A|-1-|B|-1-4\times LCS(A,B)+|A|+|B|=2 (4×LCS(A′,B′)−∣A′∣−∣B′∣)−(4×LCS(A,B)−∣A∣−∣B∣)=(4×(LCS(A,B)+1)−(∣A∣+1)−(∣B∣+1))−(4×LCS(A,B)−∣A∣−∣B∣)=(4×LCS(A,B)+4−∣A∣−1−∣B∣−1)−(4×LCS(A,B)−∣A∣−∣B∣)=4×LCS(A,B)+4−∣A∣−1−∣B∣−1−4×LCS(A,B)+∣A∣+∣B∣=2,由此可得此时 f i , j = f i − 1 , j − 1 + 2 f_{i,j}=f_{i-1,j-1}+2 fi,j=fi−1,j−1+2。
AC Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int Maxn = 5000 + 5;
int n, m;
char s1[Maxn], s2[Maxn];
int f[Maxn][Maxn];
int ans;
inline void work() {cin >> n >> m >> s1 + 1 >> s2 + 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {f[i][j] = max(f[i][j], max(f[i][j - 1], f[i - 1][j]) - 1);if (s1[i] == s2[j]) {f[i][j] = f[i - 1][j - 1] + 2;}ans = max(ans, f[i][j]);}}cout << ans << endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);work();return 0;
}
还不会?看这里。
相关文章:

CF1446B Catching Cheaters 题解 DP
Catching Cheaters 传送门 题面翻译 给我们两个字符串,让我们从中选出两个字串,算出它们的最大公共子序列长度。然后将它乘 4 4 4在减去两个字串的长度。问你这个数最大是多少。 题目描述 You are given two strings A A A and B B B representin…...

用python实现文本/图片生成视频
使用Python来生成视频通常涉及到使用一些专门的库,比如 OpenCV 或者 moviepy。下面是一个简单的例子,使用OpenCV和PIL(Python Imaging Library)来创建一个视频。 python复制代码 import cv2 import numpy as np from PIL import …...

Android Gradle Plugin、Gradle、Android Studio版本关系
参考链接 Android Gradle Plugin 与 gradle 对应关系 插件版本所需的最低 Gradle 版本8.38.48.28.28.18.08.08.07.47.57.37.47.27.3.37.17.27.07.04.2.06.7.14.1.06.54.0.06.1.13.6.0 - 3.6.45.6.43.5.0 - 3.5.45.4.13.4.0 - 3.4.35.1.13.3.0 - 3.3.34.10.13.2.0 - 3.2.14.63…...

PyTorch深度学习实战(30)——Deepfakes
PyTorch深度学习实战(30)——Deepfakes 0. 前言1. Deepfakes 原理2. 数据集分析3. 使用 PyTorch 实现 Deepfakes3.1 random_warp.py3.2 Deepfakes.py 小结系列链接 0. 前言 Deepfakes 是一种利用深度学习技术生成伪造视频和图像的技术。它通过将一个人的…...

java 修改JsonObject对象所有的Value类型为String
将JSONObject 或者JSONArray 中所有Value 为数值类型 转为String. 转换前: [{"zjlx": 201,"xm": "刘**","cbdjxxlist": [{"zspmdm": 102031201,"rybm": "43000010300000411195","jfrlx": 1…...

Vue3-47-Pinia-修改全局状态变量值的方式
说明 修改全局状态变量的值,是一个比较常规而且常见的操作。 本文就介绍四种常见的操作。 由于Option Store 和Setup Store 在修改的时候略有不同,所以本文也会将不同点体现一下。 全局状态变量的定义 包含了 Option Store 和Setup Store 两种定义方式&a…...

【Scala】——面向对象
1 Scala 包 1.1 包风格 Scala 有两种包的管理风格。 第一种 Java 的包管理风格相同,每个源文件一个包(包 名和源文件所在路径不要求必须一致),包名用“.”进行分隔以表示包的层级关系,如 com.atguigu.scala。另一种风…...

【MediaFoundation】OpenCV VideoCapture 读取音频源码
OpenCV 读取音频代码实例 在windows7 以及OpenCV4 过后可以使用 CAP_MSMF 读取音频,但是OpenCV没有播放音频的API。代码示例如下。 本文解析OpenCVCAP_MSMF 进行文件、设备的 音频读取,学习MediaFoundation 的使用。 #include <opencv2/core.hpp>…...

2024秋招,百度测试开发工程师一面
前言 大家好,今天我来回顾一下秋招中的一场很重要技术面试 一面面试官深挖我的项目经历,并提出了很多的实际场景,我现在回顾依然有很多新的认识 过程 自我介绍实习工作中,做得最好的地方是什么? 我先介绍了一下实习…...
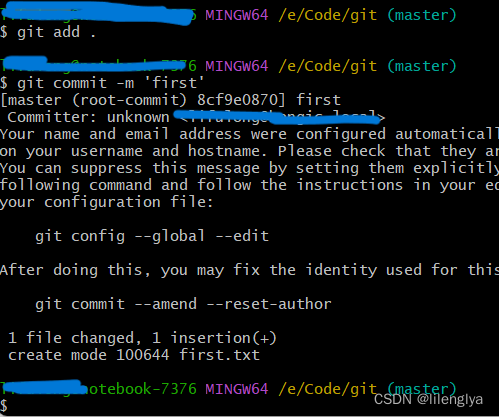
Git 使用与问题记录 二(公司快速上手版)
写在前面 记录自己学习的内容,方便后面忘记的时候查看。给像我一样的新手提供一点参考 正文 上一章已经安装好了Git,如何使用呢。我这里会分享两种办法,第一种是在VS2022中克隆代码,修改和提交;第二种是用命令提交。…...

【C语言小游戏】贪吃蛇
文章目录 1.引言2.运行图2.涉及知识3 Windows API3.1 控制台3.2 控制台屏幕坐标3.3 操作句柄3.4 控制台屏幕光标3.5 监视按键 4. 设计说明5. 完整代码 1.引言 使⽤C语⾔在Windows环境的控制台中模拟实现经典⼩游戏贪吃蛇 实现基本的功能: 贪吃蛇地图绘制蛇吃⻝物的…...

价值7500的在线授权网站源码支持IP+域名+双向授权全开源
PHP授权验证更新系统完整版,一键更新系统,一键卡密生成自助授权功能,域名ip双重验证功能等等 修复盗版检测,确保实时查看盗版 修复在线加密系统,一键加密 授权系统几乎所有的程序都能整合使用,包括您的app和计算机程序…...

haiku实现门控多头注意力模块
在多头注意力机制中,通常输入的数据包括查询(Q)、键(K)和值(V)。这些数据的维度以及权重矩阵的维度在多头注意力机制中扮演关键角色。下面对数据及权重的维度进行解释: 输入数据&…...

【React 常用的 TS 类型】持续更新
1)定义样式的 TS 类型 【 React.CSSProperties 】 一般定义样式时需要的类型限制,如下: const customStyle: React.CSSProperties {color: blue,fontSize: 16px,margin: 10px,}; 2)定义 Input Ref 属性时的 TS 类型限制 【 R…...

打破传统边界,VR技术与六西格玛设计理念的创新融合!
在科技飞速发展的今天,虚拟现实(VR)技术以其独特的沉浸式体验,正在改变我们的生活和工作方式。然而,要让VR真正成为主流,我们必须解决一些关键问题,其中最重要的就是用户体验。六西格玛设计&…...

[uniapp] uni-ui+vue3.2小程序评论列表组件 回复评论 点赞和删除
先看效果 下载地址 uni-app官方插件市场: cc-comment组件 环境 基于vue3.2和uni-ui开发; 依赖版本参考如下: "dependencies": {"dcloudio/uni-mp-weixin": "3.0.0-3090820231124001","dcloudio/uni-ui": "^1.4.28","…...
:TongLINKQ常用命令)
TongLINKQ(3):TongLINKQ常用命令
启动: tlq 暂停: tlq -cabort -y -w1 查看lic信息: tlqstat –lic 查看队列消息: tlqstat -qcu qcu名 -c 查看发送连接状态: tlqstat -snd qcu名 -1 -ct 1 查看指定的Qcu连接状态: tlqsta…...

抽水马桶出水慢解决记录
今天分享一些修马桶的小心得(雾) 家里的马桶出水很好,但是水却不怎么被冲下去(出水很慢),这会导致内容物滞留,造成很不好的使用体验。 出于成本考虑,首先选择自己维修。 首先直接…...

img标签的奇怪问题
本来只是为实现一个轮播图,img的url地址是从后端接口获取的,但不巧的是url地址的图片都过期了。 因为懒得重新到网上找图,就想直接用一下本地的图片,简单的想法遇到一堆问题。 问题一: 因为是springboot项目…...

深入探究Hibernate:优雅、强大的Java持久化框架
目录 1、前言 2、Hibernate简介 2.1 什么是Hibernate 2.2 为什么选择Hibernate 3、Hibernate核心概念 3.1 实体类和映射文件 3.2 数据库表和持久化类的映射 3.3 主键生成策略 3.4 持久化操作 3.5 查询语言(HQL和Criteria) 3.6 事务管理 4、Hibernate配置与连接 4…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
