数据结构:二叉树
数据结构:二叉树
文章目录
- 数据结构:二叉树
- 1.一些特殊的二叉树
- 1.满二叉树
- 2.完全二叉树
- 2.手动创建一颗二叉树
- 3.二叉树深度优先遍历
- 4.二叉树层序遍历
- 5.二叉树基础操作
- 1.创建二叉树
- 2.二叉树节点个数
- 3.二叉树叶子节点个数
- 4.二叉树的高度
- 5.二叉树第k层节点个数
- 6.二叉树查找值为x的节点
- 7.层序遍历
- 8.二叉树销毁
- 9.判断二叉树是否是完全二叉树
二叉树
1.一些特殊的二叉树
1.满二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果==一个二叉树的层数为K,且结点总数是2^k-1== ,则它就是满二叉树。
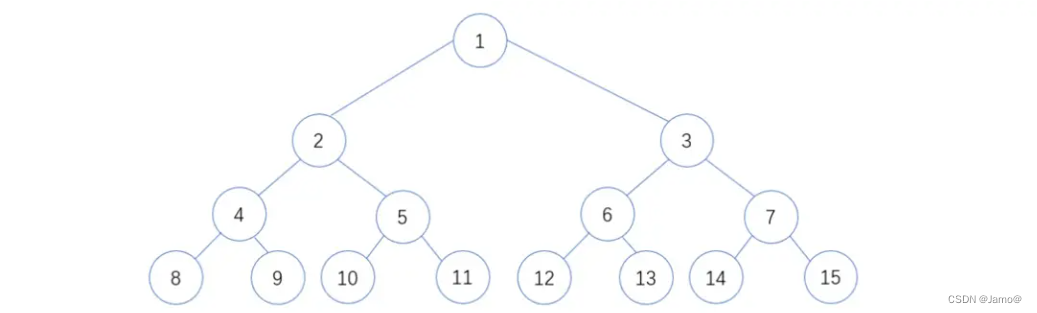
2.完全二叉树
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一 一对
应时称之为完全二叉树。 **要注意的是满二叉树是一种特殊的完全二叉树**。
2.手动创建一颗二叉树
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>// 手动快速创建一棵简单的二叉树来测试三种深度优先遍历方式(前中后序遍历)(后续学习递归构建二叉树才是真正常用的方法)
typedef int BinaryTreeDataType;typedef struct BinaryTreeNode
{BinaryTreeDataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;BTNode* CreateBTNode(BinaryTreeDataType x)
{BTNode* NewBTNode = (BTNode*)malloc(sizeof(BTNode));if (NewBTNode == NULL){perror("malloc fail");exit(-1);}NewBTNode->val = x;NewBTNode->left = NULL;NewBTNode->right = NULL;return NewBTNode;
}
BTNode* CreatBinaryTree()
{BTNode* root = CreateBTNode(1);BTNode* node2 = CreateBTNode(2);BTNode* node3 = CreateBTNode(3);BTNode* node4 = CreateBTNode(4);BTNode* node5 = CreateBTNode(5);BTNode* node6 = CreateBTNode(6);root->left = node2;root->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return root;
}
3.二叉树深度优先遍历
前序、中序和后序遍历都属于「深度优先遍历 depth-first traversal, DFS」,它体现了一种“先走到尽头,再回溯继续”的遍历方式。
// 前序遍历
void Preorder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);Preorder(root->left);Preorder(root->right);
}// 中序遍历
void Inorder(BTNode* root)
{if (root == NULL){printf("N ");return;}Inorder(root->left);printf("%d ", root->val);Inorder(root->right);
}
// 后序遍历
void Postorder(BTNode* root)
{if (root == NULL){printf("N ");return;}Postorder(root->left);Postorder(root->right);printf("%d ", root->val);
}
4.二叉树层序遍历
层序遍历本质上属于「广度优先遍历 breadth-first traversal, BFS」,它体现了一种“一圈一圈向外扩展”的逐层遍历方式。
利用队列先进先出的性质:父亲先进队列,父亲出来时再带孩子进队列
void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列 实现二叉树的层序遍历 (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);while (!Empty(queuehead)){// 遍历二叉树入队列并挨个打印值BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}// 销毁队列Destroy(&queuehead);
}
5.二叉树基础操作
1.创建二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
// 通过 前序遍历 的数组"ABD##E#H##CF##G##"构建二叉树BTNode* BinaryTreeCreate(BTDataType* parray, int* pi)
{// 前序遍历创建二叉树if (parray[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = parray[(*pi)++];root->left = BinaryTreeCreate(parray, pi);root->right = BinaryTreeCreate(parray, pi);return root;
}
2.二叉树节点个数
/*
写法一:遍历计数
*/
int BinaryTreeSize(BTNode* root)
{// 遍历二叉树计算节点个数static int size = 0;// 函数中使用静态不能完全解决问题,无法处理多次计算的情况if (root == NULL){return 0;}size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}/*
写法二:递归分治子问题
*/
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//节点个数 = 左子树节点个数 + 右子树节点个数 + 1
}
3.二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}// 叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数return root->left == NULL && root->right == NULL ? 1 : BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
4.二叉树的高度
/*
写法1:
*/
int BinaryTreeHight(BTNode* root)
{if (root == NULL){return 0;}// 此处递归分治多次重复导致效率过低(原因是此逻辑中比较时候进行了递归分治,计算的时候又重复进行了计算)return BinaryTreeHight(root->left) > BinaryTreeHight(root->right)|| BinaryTreeHight(root->left) == BinaryTreeHight(root->right)? BinaryTreeHight(root->left) + 1: BinaryTreeHight(root->right) + 1;// 二叉树的高度 = 左子树与右子树相比,高度更高的那棵树的高度 + 1
}/*
写法2:
*/
int BinaryTreeHight(BTNode* root)
{if (root == NULL){return 0;}//提前记录高度int lefthight = BinaryTreeHight(root->left);int righthight = BinaryTreeHight(root->right);// 二叉树的高度 = 左子树与右子树相比,高度更高的那棵树的高度 + 1return lefthight > righthight|| lefthight == righthight? lefthight + 1: righthight + 1;}
5.二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (root != NULL && k == 1){return 1;}// 问题拆分:第k层节点个数 = 左子树第k-1层节点数 + 右子树第k-层节点数return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);}
6.二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}// 前序遍历二叉树寻找该节点if (root->data == x){return root;}else{BTNode* leftnode = BinaryTreeFind(root->left, x);if (leftnode){return leftnode;}BTNode* rightnode = BinaryTreeFind(root->right, x);if (rightnode){return rightnode;}//如果左右节点都不是我们要找的该节点则返回空if (leftnode == NULL && rightnode == NULL){return NULL;}}
}
7.层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列 实现二叉树的层序遍历 (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);while (!Empty(queuehead)){// 遍历二叉树入队列并挨个打印值BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}// 销毁队列Destroy(&queuehead);
}
变形:如何控制一层一层打印并换行?
// 层序遍历变形换行打印
void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列 实现二叉树的层序遍历 (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);// 根据每一层的数据的个数得出打印多少次后进行一次换行int levelsize = 1;while (!Empty(queuehead)){// 一层一层出while (levelsize--){// 遍历二叉树入队列BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}printf("\n");levelsize = Size(queuehead);}// 销毁队列Destroy(&queuehead);
}
8.二叉树销毁
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{// 走后序遍历更方便销毁if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}
9.判断二叉树是否是完全二叉树
思路:完全二叉树只有最后一层会出现 NULL 值,而且出现了 NULL 值,则后面不会再出现非空的值。我们可以通过层序遍历的思想,一层一层遍历,如果遇到空结点,记录一下,然后继续遍历,若是后面出现了非空值,则说明该二叉树不是完全二叉树。
// 判断二叉树是否是完全二叉树
// 参数:root,一个指向二叉树根节点的指针
bool BinaryTreeComplete(BTNode* root)
{Queue* queuehead = Init();// 将二叉树的根节点入队列Push(&queuehead, root);while (!Empty(queuehead)){BTNode* front = Peek(&queuehead);if (front == NULL){break;}Pop(&queuehead);Push(&queuehead, front->left);Push(&queuehead, front->right);}// 当第一次遍历的时候出道空代表应当结束了,第二次继续往后遍历如果队列中还有非空代表不是完全二叉树while (!Empty(queuehead)){BTNode* front = Peek(&queuehead);Pop(&queuehead);if (front != NULL){return false;}}return true;
}

相关文章:

数据结构:二叉树
数据结构:二叉树 文章目录 数据结构:二叉树1.一些特殊的二叉树1.满二叉树2.完全二叉树 2.手动创建一颗二叉树3.二叉树深度优先遍历4.二叉树层序遍历5.二叉树基础操作1.创建二叉树2.二叉树节点个数3.二叉树叶子节点个数4.二叉树的高度5.二叉树第k层节点个…...
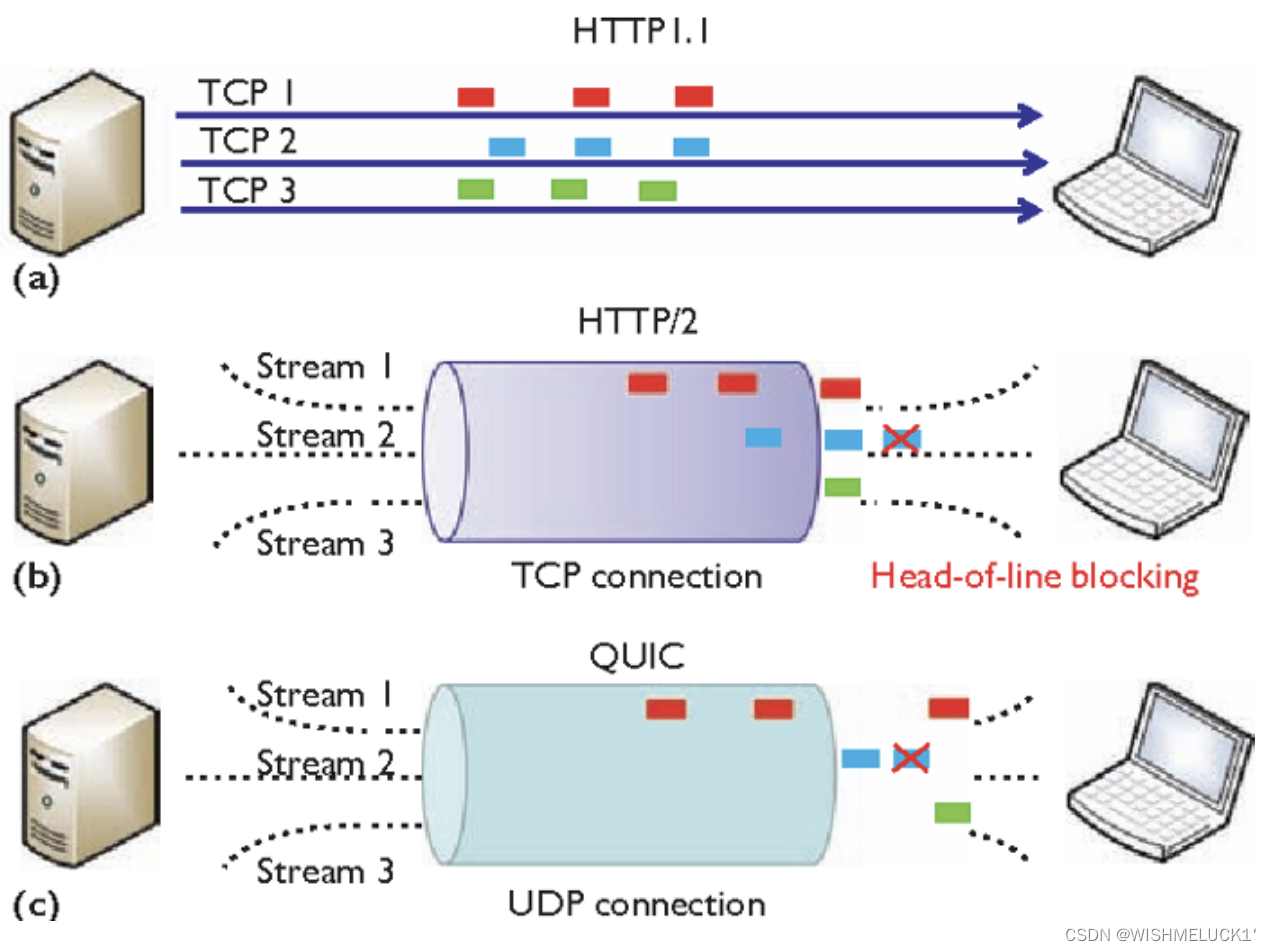
HTTP超文本传输协议
原文链接: 1.5 万字 40 张图解 HTTP 常见面试题(值得收藏)_图解http 小林-CSDN博客https://blog.csdn.net/qq_34827674/article/details/124089736?ops_request_misc%257B%2522request%255Fid%2522%253A%2522170521531616777224478386%252…...
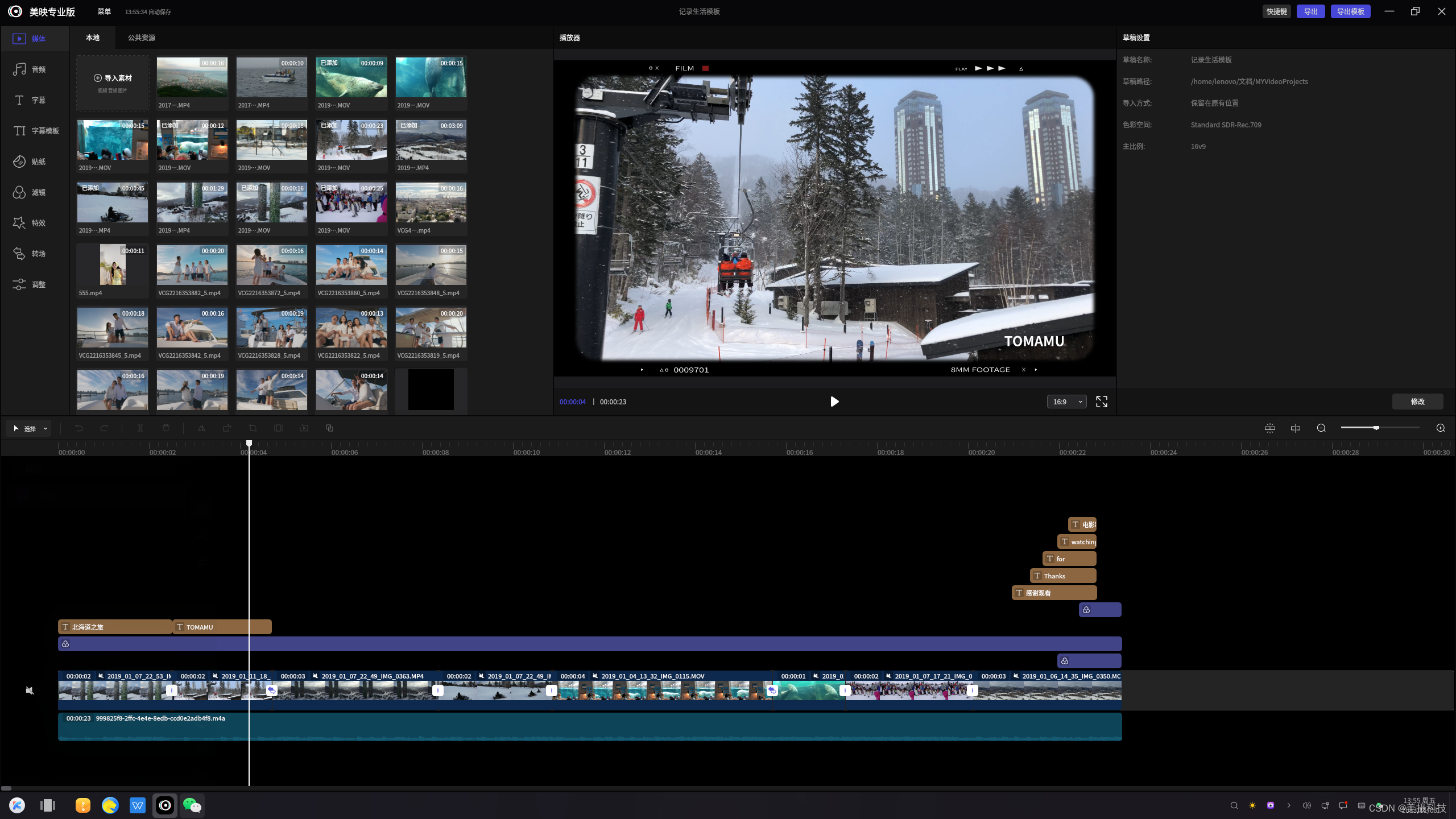
视频SDK的技术架构优势和价值
为了满足企业对于高质量视频的需求,美摄科技推出了一款强大的视频SDK(软件开发工具包),旨在帮助企业轻松实现高效、稳定的视频功能,提升用户体验,增强企业竞争力。 一、美摄视频SDK的技术实现方式 美摄视…...

Invalid bound statement (not found)(xml文件创建问题)
目录 解决方法: 这边大致讲一下我的经历,不想看的直接点目录去解决方法 今天照着老师视频学习,中间老师在使用动态SQL时,直接复制了一份,我想这么简单的一个,我直接从网上找内容创建一个好了,…...

正则表达式2 常见模式
继上次的正则表达式速攻1/2-CSDN博客 还有一些常见的匹配模式可以直接使用 电子邮箱 xxxxxx.域名 的情况 \b[A-Za-z0-9._%-][A-Za-z0-9.-]\.[A-Z|a-z]{2,}\bhttp或者https网址 的情况 http[s]?://(?:[a-zA-Z]|[0-9]|[$-_.&]|[!*\\(\\),]|(?:%[0-9a-fA-F][0-9a-fA-F…...

前端对接电子秤、扫码枪设备serialPort 串口使用教程
因为最近工作项目中用到了电子秤,需要对接电子秤设备。以前也没有对接过这种设备,当时也是一脸懵逼,脑袋空空。后来就去网上搜了一下前端怎么对接,然后就发现了SerialPort串口。 Serialport 官网地址:https://serialpo…...
整数转罗马数字)
LeeCode前端算法基础100题(18)整数转罗马数字
一、问题详情: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如, 罗马数字 2 写做 II ,即为两个并列的 1…...
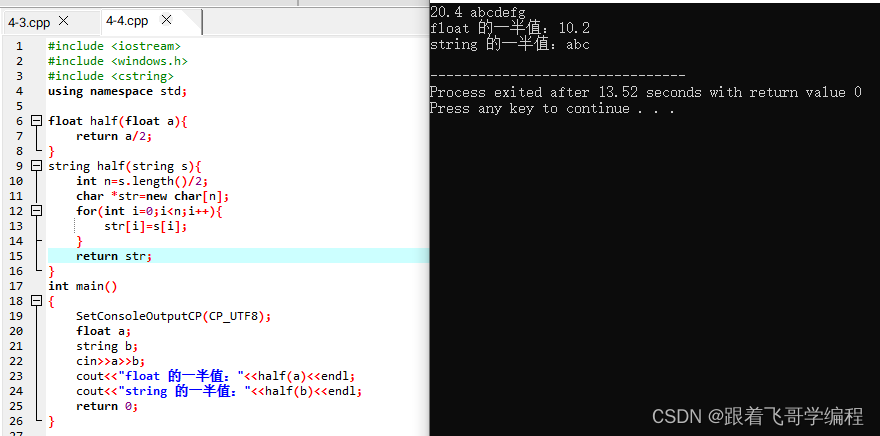
【C++ 程序设计入门基础】- 第4节-函数
1、函数 函数是对实现某一功能的代码的模块化封装。 函数的定义: 标准函数: 输入 n 对整数的 a、b ,输出它们的和。 #include <iostream> #include <windows.h> using namespace std;int add(int a,int b);//函数原型声明int…...

华为数通HCIA题库(750题)
完整题库在这里:华为数通HCIA-RS题库注释版-加水印.pdf资源-CSDN文库 此处只节选几题。 1.网络管理员在网络中捕获到了一个数据帧,其目的MAC地址是01-00-5E-AO-B1-C3。关于该MAC地址的说法正确的是( )。 A.它是一个单播MAC地址 B.它是一个广播…...

SpringIOC之support模块GenericXmlApplicationContext
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...
CCF认证+蓝桥杯习题训练
贪心 *上取整公式* *代码展示* #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 1e5 10;typedef long long LL;int v[N] , a[N];int main() {int n , d;cin >> n >> d;for(int i 1 ; i < n…...
vue前端开发自学基础,动态切换组件的显示
vue前端开发自学基础,动态切换组件的显示!这个是需要借助于,一个官方提供的标签,名字叫【Component】-[代码demo:<component :is"ComponetShow"></component>]。 下面看看代码详情。 <template><h3>动态…...

16.桥接模式
桥接模式 介绍 桥接模式是一种结构型设计模式,它通过将抽象部分与实现部分分离,使它们可以独立变化。这种模式通过组合的方式来实现,而不是继承。桥接模式通过将抽象和实现解耦,从而实现抽象和实现的分离,使得系统更加…...
【网络安全】【密码学】【北京航空航天大学】实验一、数论基础(上)【C语言和Java实现】
实验一、数论基础(上) 一、实验目的 1、通过本次实验,熟悉相关的编程环境,为后续的实验做好铺垫; 2、回顾数论学科中的重要基本算法,并加深对其的理解,为本学期密码学理论及实验课程打下良好…...

Go语言的sync.Pool如何使用?使用场景具体有哪些?
sync.Pool 是 Go 标准库中提供的一个对象池(Object Pool)的实现。对象池是一种用于缓存和复用对象的机制,可以在一定程度上减轻内存分配的开销。sync.Pool 专门用于管理临时对象,适用于一些需要频繁创建和销毁的短暂对象ÿ…...

MySQL单表查询练习题
一、创建表的素材 表名:worker——表中字段均为中文,比如:部门号、工资、职工号、参加工作等 CREATE TABLE worker ( 部门号 int(11) NOT NULL, 职工号 int(11) NOT NULL, 工作时间 date NOT NULL, 工资 float(8,2) NOT NULL, 政治面貌 …...

Spring MVC中@Controller和@RestController的区别
Controller 和 RestController 是 Spring MVC 中用于处理 HTTP 请求的注解,它们有以下区别: 返回值处理方式: Controller 用于定义一个传统的 Spring MVC 控制器,它的方法通常返回视图名称或 ModelAndView 对象,由视图…...
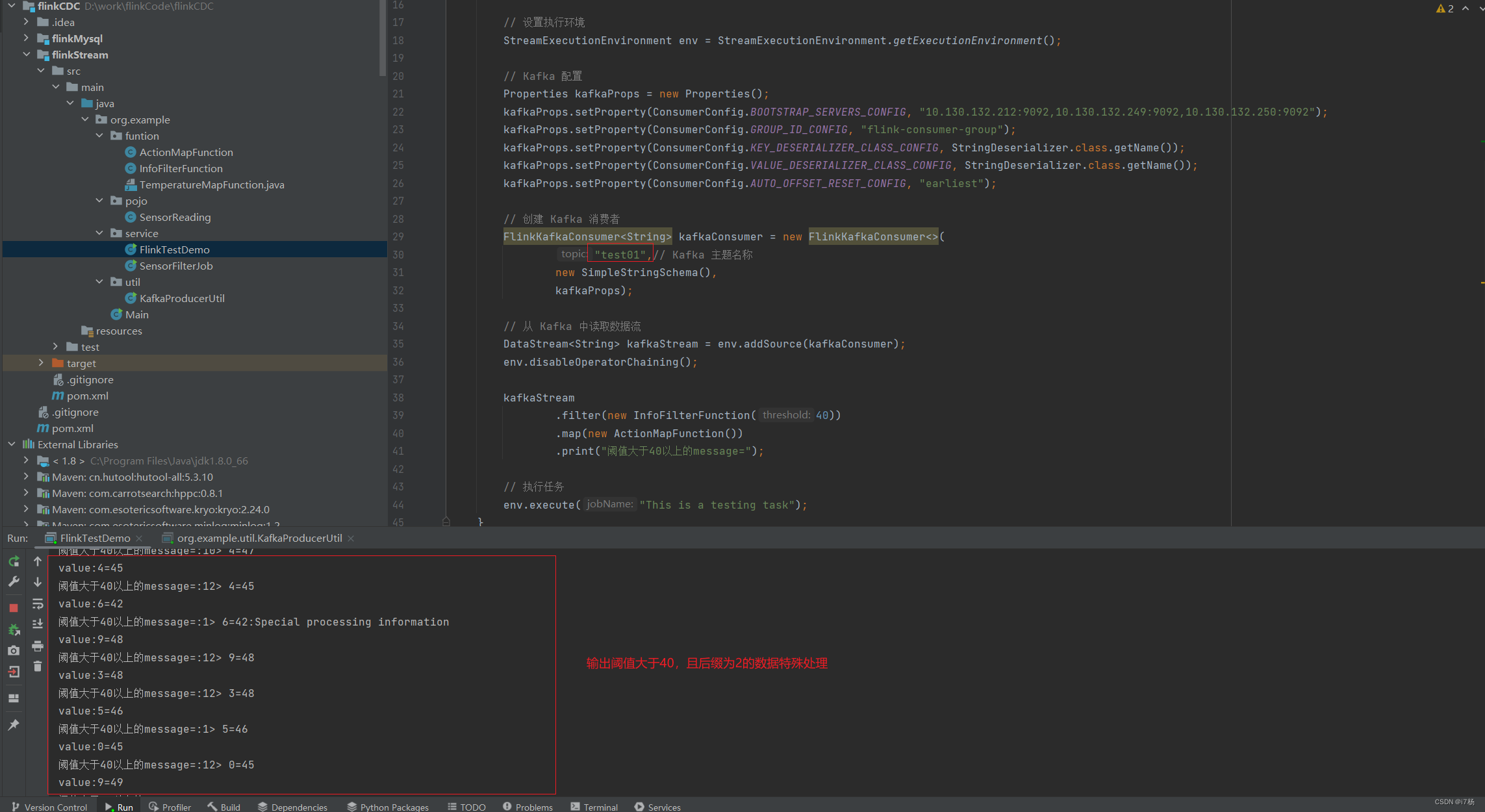
Flink定制化功能开发,demo代码
前言: 这是一个Flink自定义开发的基础教学。本文将通过flink的DataStream模块API,以kafka为数据源,构建一个基础测试环境;包含一个kafka生产者线程工具,一个自定义FilterFunction算子,一个自定义MapFunctio…...

Edge浏览器入门
关于作者: CSDN内容合伙人、技术专家, 从零开始做日活千万级APP,带领团队单日营收超千万。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业化变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览…...

Go语言的调度器
简介 Go语言的调度器是一个非常强大的工具,它可以帮助我们轻松地实现并发编程。调度器的工作原理是将多个协程映射到多个操作系统线程上,并根据协程的状态来决定哪个协程应该在哪个线程上运行。 调度器有两种主要策略: 协作式调度…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
