Windows无法登录管理路由器故障排查
问题描述
家里的路由器使用拨号上网,路由器DHCP分发IP的范围是192.168.1.0/24。默认使用192.168.1.1管理路由器。然后拨号上网成功后,修改了私网IP的分发范围:192.168.5.1-192.168.5.10。为了防止有人蹭网,只分配的10个IP地址。修改完路由器重启,重启之后我的电脑无法通过192.168.5.1登录到路由器的管理页面,但是可以正常的使用网络,手机、iPad以及室友的电脑均可以正常管理路由器。
故障现象
- 路由器的LAN口DHCP配置

- 管理路由器测试

这里我当时没有注意到右上角的LoopBack 0的IP是192.168.5.1,问题就是出在这里
故障排查
- 在CMD中通过
route print命令,查看路由表

发现有两个到达192.168.5.0段的路由,一个是到从无线网卡(192.168.5.51)发出的,一个是直接到192.168.5.1网关的。同时我本地还有一个192.168.5.1的路由(就很奇怪)
- 测试与192.168.5.1的连通性
- 可以ping通,但是telnet 80端口不通

- 可以ping通,但是telnet 80端口不通
这个时候我突然想到,由于我做实验习惯性用192.168.5.0段的IP,之前使用环回网卡做过实验,好像配置的IP是192.168.5.1!!!
- 使用
Win+R输入ncpa.cpl打开网卡适配器管理

果然问题是出在这里!
故障解决
- 删除环回网卡LoopBack 0的IP,或者换成其它网端的IP
- 成功登录路由器!
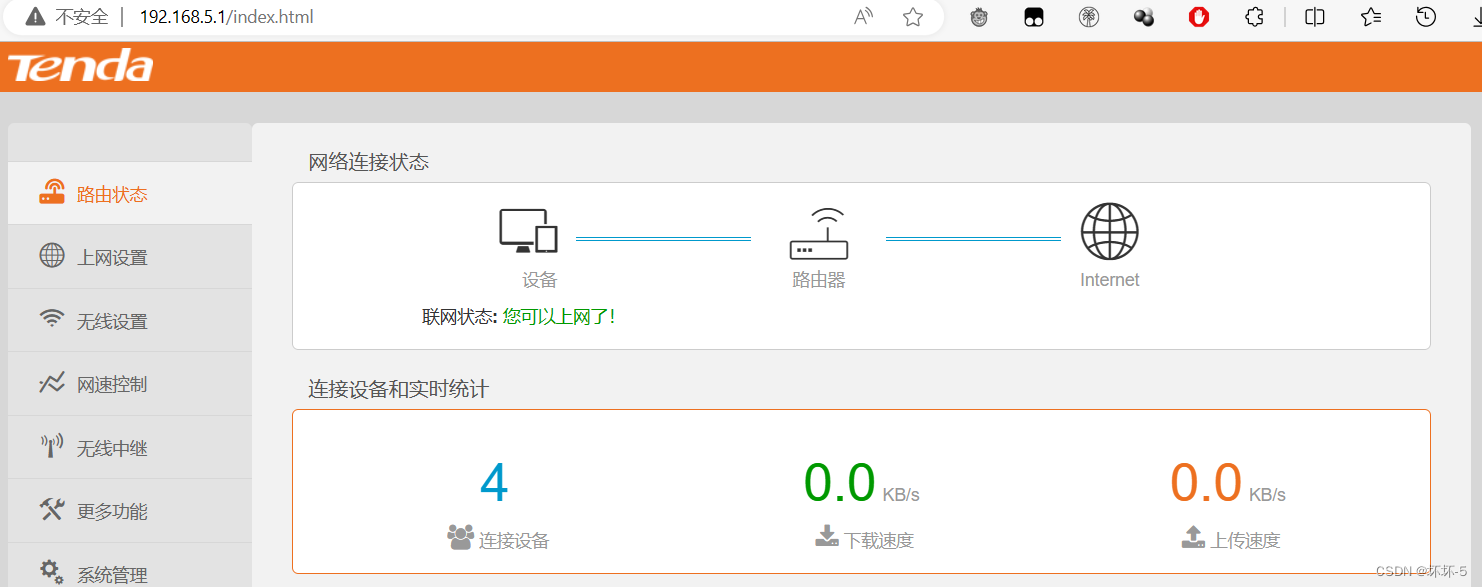
- 成功登录路由器!
- 除了删除换回网卡的IP,也可以尝试修改路由器的DHCP分发IP的网段
以上内容均属原创,如有不详或错误,敬请指出。
相关文章:

Windows无法登录管理路由器故障排查
问题描述 家里的路由器使用拨号上网,路由器DHCP分发IP的范围是192.168.1.0/24。默认使用192.168.1.1管理路由器。然后拨号上网成功后,修改了私网IP的分发范围:192.168.5.1-192.168.5.10。为了防止有人蹭网,只分配的10个IP地址。修…...
通义灵码 - 免费的阿里云 VS code Jetbrains AI 编码辅助工具
系列文章目录 前言 通义灵码,是阿里云出品的一款基于通义大模型的智能编码辅助工具,提供行级/函数级实时续写、自然语言生成代码、单元测试生成、代码注释生成、代码解释、研发智能问答、异常报错排查等能力,并针对阿里云 SDK/OpenAPI 的使用…...

山脉数组的峰顶索引
一、题目描述 852. 山脉数组的峰顶索引 符合下列属性的数组 arr 称为 山脉数组 : arr.length > 3存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > .…...
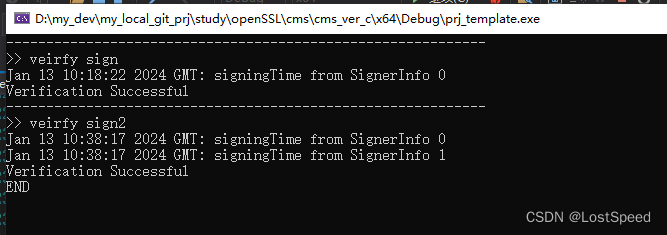
openssl3.2 - 官方demo学习 - cms - cms_ver.c
文章目录 openssl3.2 - 官方demo学习 - cms - cms_ver.c概述运行结果笔记END openssl3.2 - 官方demo学习 - cms - cms_ver.c 概述 CMS验签, 将单独签名和联合签名出来的签名文件都试试. 验签成功后, 将签名数据明文写入了文件供查看. 也就是说, 只有验签成功后, 才能看到签名…...

数据结构:堆和堆排序
数据结构:堆和堆排序 文章目录 数据结构:堆和堆排序1.二叉树的存储结构1.顺序结构2.链式结构 2.堆3.堆的实现4.堆排序(选择排序中的一类)1. 基本思想2.代码实现 1.二叉树的存储结构 1.顺序结构 顺序结构存储就是使用数组来表示一…...

力扣精选算法100题——水果成篮(滑动窗口专题)
本题链接👉水果成篮 第一步:了解题意 我就按照实例1来进行对这题的理解。 1代表种类类型,这个数组里面有2个种类类型 ps:种类1和种类2 ,只不过种类1是有2个水果,种类2有一个水果,共计3个水果。 本题需要解…...

【提示学习论文六】MaPLe: Multi-modal Prompt Learning论文原理
文章目录 MaPLe: Multi-modal Prompt Learning 多模式提示学习文章介绍动机MaPLe:Multi-modal Prompt Learning 模型结构1、Deep Language Prompting 深度语言提示2、Deep Vision Prompting 深度视觉提示3、Vision Language Prompt Coupling 视觉语言提示耦合提示耦合过程 实验…...
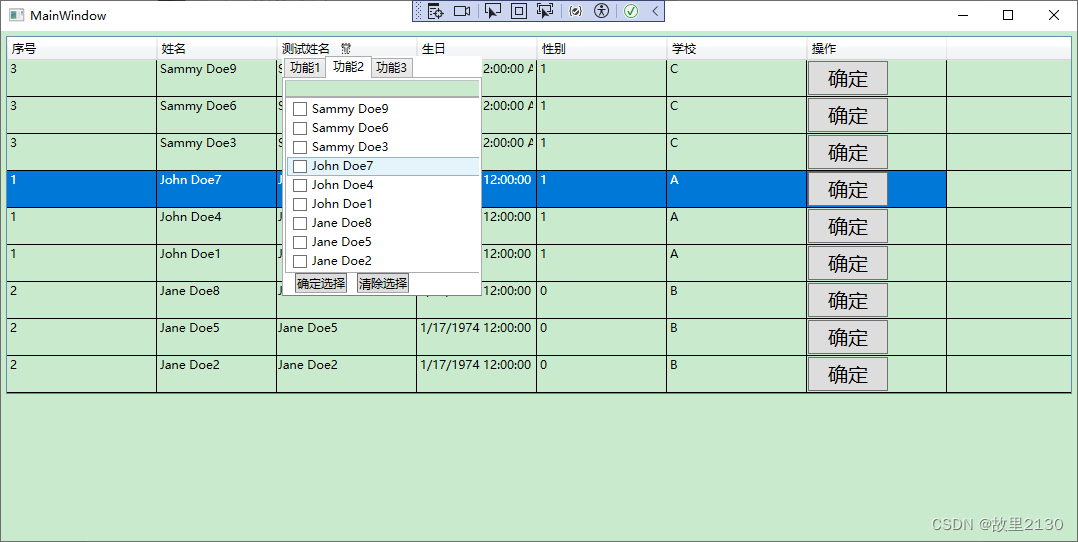
wpf使用Popup封装数据筛选框
(关注博主后,在“粉丝专栏”,可免费阅读此文) 类似于DevExpress控件的功能 这是DevExpress的winform筛选样式,如下: 这是DevExpress的wpf筛选样式,如下: 这是Excel的筛选样式,如下: 先看效果 本案例使用wpf原生控件封装,功能基本上都满足,只是颜色样式没有写…...

微信小程序 - 视图与逻辑 介绍
文章目录 视图与逻辑一、页面导航1、页面导航 - 声明式导航1.1 导航到tabBar页面1.2 导航到非tabBar页面1.3 后退导航 2、页面导航 - 编程式导航2.1 导航到tabBar页面2.2 导航到非tabBar页面2.3 后退导航 3、页面导航 - 导航传参3.1 声明式导航传参3.2 编程式导航传参3.3 在 on…...
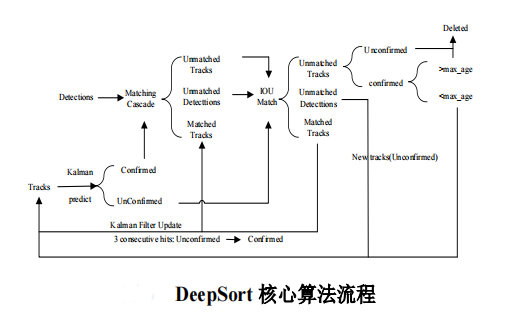
大创项目推荐 深度学习疫情社交安全距离检测算法 - python opencv cnn
文章目录 0 前言1 课题背景2 实现效果3 相关技术3.1 YOLOV43.2 基于 DeepSort 算法的行人跟踪 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习疫情社交安全距离检测算法 ** 该项目较为新颖,适合作为竞赛…...

c语言-库函数strstr()、strtok()、strerror()介绍
文章目录 前言一、库函数strstr()1.1 strstr()介绍1.2 strstr()模拟实现 二、库函数strtok()2.1 strtok()介绍 三、库函数strerror()3.1 strerror()介绍 总结 前言 本篇文章介绍c语言库函数strstr()、strtok()、strerror()的使用。 一、库函数strstr() 1.1 strstr()介绍 str…...
RIP【新华三与华为区别】
【介绍】 rip分为rip 1 与 rip 2 ,rip 2 是对 rip 1 的一种升级,rip 2 可以进行认证等功能 【命令】 新华三: [HC3-R1] rip #启用rip [HC3-R1-rip] version 2 #告知rip 版本号 [HC3-R1-rip] network 192.168.1.0 #宣告其网段 [HC3-R1-rip] …...

Python从入门到精通秘籍四
Python速成,知识点超详细,跟着这个系列边输入边学习体会吧! 一、Python的判断语句的综合案例 下面是一个使用代码示例来详细说明Python判断语句的综合案例,通过用户输入来实现简单的登录验证: # 提示用户输入用户名和密码 username = input("请输入用户名:")…...

rk3568下SoftBusDumpDeviceInfo执行错误—鸿蒙开发已解决
文章目录 项目场景:问题描述原因分析:解决方案:此Bug解决方案总结寄语项目场景: 最近也是遇到了这个问题,看到网上也有人在询问这个问题,本文总结了自己和其他人的解决经验,解决了rk3568下SoftBusDumpDeviceInfo执行错误的问题。 命令行运行 SoftBusDumpDeviceInfo,测…...

Vue 3 Composition API 详解
一、引言 在Vue 3中,引入了一个新的Composition API,旨在提供一种更灵活和可重用的方式来组织组件代码。Composition API基于函数式编程思想,允许开发者将逻辑和状态管理逻辑分离,使代码更加清晰和可维护。 二、Composition API…...
API设计:从基础到最佳实践
1*vWvkkgG6uvgmJT8GkId98A.png 在这次深入探讨中,我们将深入了解API设计,从基础知识开始,逐步进阶到定义出色API的最佳实践。 作为开发者,你可能对许多这些概念很熟悉,但我将提供详细的解释,以加深你的理解…...

每日汇评:由于中东危机削弱了风险偏好,欧元将在1.0900附近波动
随着中东危机的加深,欧元兑美元面临大幅抛售; 由于高通胀,欧洲央行决策者推迟了市场对早期降息的预期; 市场将受到周三公布的美国零售销售数据的影响; 持续的中东紧张局势增强了对避险资产的吸引力,而风险感…...

算法每日一题:删除子串后的字符串最小长度 | 栈 | 字符串
大家好,我是星恒 今天给大家带来的是一道另类的栈的应用 话不多说,我们直接来体验 题目:leetcode 2696 给你一个仅由 大写 英文字符组成的字符串 s 。你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 …...
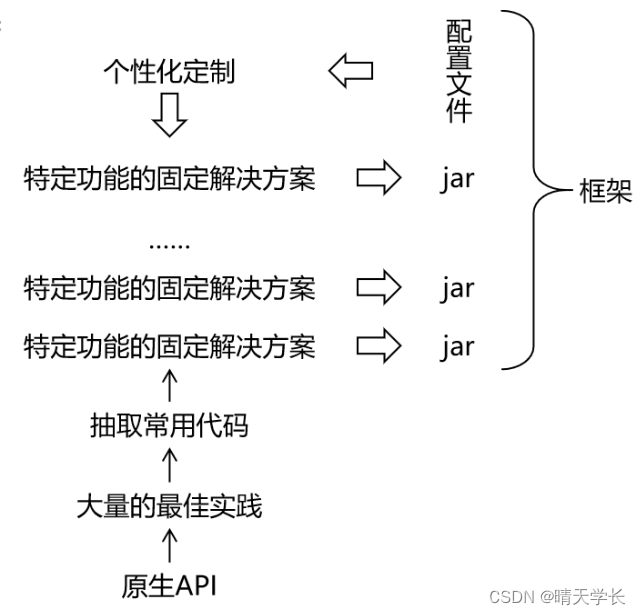
SpringFramework实战指南(一)
SpringFramework实战指南(一) 一、技术体系结构1.1 总体技术体系1.2 框架概念和理解 一、技术体系结构 1.1 总体技术体系 单一架构 一个项目,一个工程,导出为一个war包,在一个Tomcat上运行。也叫all in one。 单一架…...

AtCoder ABC198
本期F为群论题,很有难度。 C - Compass Walking 为了避免精度问题,采用二分推算。但是要小心结果为1的地方。 R 2 ∗ k 2 ≥ x 2 y 2 R^2*k^2\geq x^2y^2 R2∗k2≥x2y2 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
