关于【网格结构】岛屿类问题的通用解法DFS(深度遍历)遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题,自己总结加上看了力扣大佬的知识总结写下本篇文章,我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
目录
一、网格类问题的DFS遍历方法
1.1网格问题基本概念
1.2 DFS的基本结构
1.3 如何避免重复遍历
二、岛屿经典例题
2.1 岛屿数量
2.2 岛屿的周长
2.3 单词搜索
一、网格类问题的DFS遍历方法
1.1网格问题基本概念
网格问题是由 m×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。 数字为1的格子连接起来就形成一个岛屿。
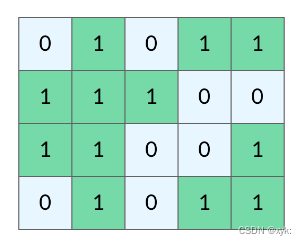
1.2 DFS的基本结构
首先我们要确定访问的下一个节点以及停止的边界,那么首先网格结构中的每个格子可以向四周延伸,分别为上,下,左,右,对于格子(r,c)来说,对应的四个坐标分别为(r+1,c)、(r-1,c)、(r,c-1)、(r,c+1)。

其次超出格子的边界是什么?是grid[r][c]出现下标越界异常的格子,也就是那些超出范围的格子。
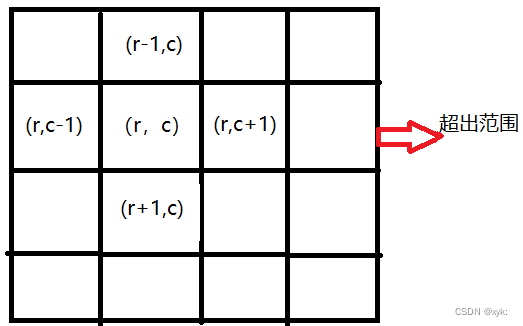
这样我们就得到了网格DFS遍历的框架代码:
public void infect(char[][] grid,int i ,int j){
//超出范围if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length){return;}
//访问上,下,左,右infect(grid,i+1,j);infect(grid,i-1,j);infect(grid,i,j+1);infect(grid,i,j-1);
}1.3 如何避免重复遍历
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。
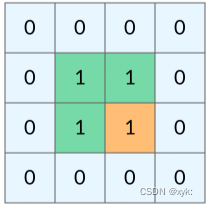
如何避免这样的重复遍历呢?答案是将已经遍历过的格子的值修改一下,每次走过一个格子就修改格子的值。以岛屿问题为例,我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子,就把格子的值改为 2,这样当我们遇到 2 的时候,就知道这是遍历过的格子了。
public void infect(char[][] grid,int i ,int j){if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length ){return;}grid[i][j] = '2';infect(grid,i+1,j);infect(grid,i-1,j);infect(grid,i,j+1);infect(grid,i,j-1);}二、岛屿经典例题
2.1 岛屿数量
岛屿类问题的通用解法、DFS 遍历框架 - 岛屿数量 - 力扣(LeetCode)
- 0 —— 海洋格子
- 1 —— 陆地格子(未遍历过)
- 2 —— 陆地格子(已遍历过)
class Solution {public int numIslands(char[][] grid) {int islandNum = 0;for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[0].length; j++) {if (grid[i][j] == '1'){infect(grid,i,j);islandNum++;}}}return islandNum;}public void infect(char[][] grid,int i ,int j){if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1'){return;}grid[i][j] = '2';infect(grid,i+1,j);infect(grid,i-1,j);infect(grid,i,j+1);infect(grid,i,j-1);}
}2.2 岛屿的周长
463. 岛屿的周长 - 力扣(LeetCode)
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
我们可以将岛屿的周长中的边分为两类,如下图所示。黄色的边是与网格边界相邻的周长,而蓝色的边是与海洋格子相邻的周长。
当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候,实际上就经过了一条黄色的边;而当函数因为「当前格子是海洋格子」返回的时候,实际上就经过了一条蓝色的边。
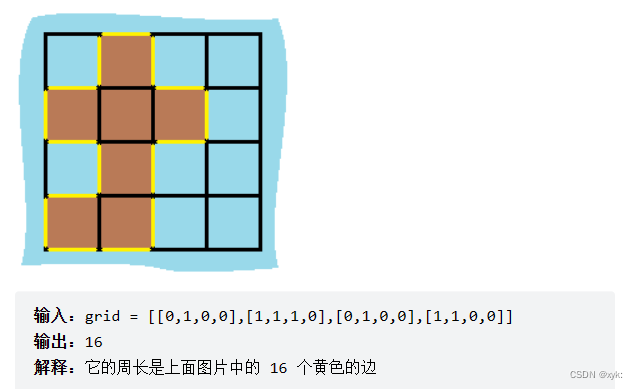
本题我们可以再次嵌套DFS的框架,但是要增加几处地方,实际上,岛屿的周长是计算岛屿全部的「边缘」,而这些边缘就是我们在 DFS 遍历中,
dfs函数返回的位置。
class Solution {public int islandPerimeter(int[][] grid) {for (int r = 0; r < grid.length; r++) {for (int c = 0; c < grid[0].length; c++) {if (grid[r][c] == 1){return dfs(grid,r,c);}}}return 0;}public int dfs(int[][] grid,int r,int c){if (r < 0 || r >= grid.length ||c < 0 || c >= grid[0].length ){return 1;}if (grid[r][c] == 0){return 1;}if (grid[r][c] != 1){return 0;}grid[r][c] = 2;return dfs(grid,r-1,c)+dfs(grid,r+1,c)+dfs(grid,r,c-1)+dfs(grid,r,c+1);}
}
2.3 单词搜索
79. 单词搜索 - 力扣(LeetCode)
给定一个
m x n二维字符网格board和一个字符串单词word。如果word存在于网格中,返回true;否则,返回false。
本题在使用上面的DFS框架时,要加上回溯,因为当搜索一次时,会更改当前的格子的值,
如果我在DFS的过程中不改矩阵的状态,那我就会出现重复搜索的情况啊,这可不行,因此矩阵是必须得改的。那就只剩下一个办法了,每次DFS的过程中修改矩阵,DFS完了再把矩阵给改回去呗,这就是回溯!
那么什么是剪枝呢?所谓剪枝就是我在dfs的时候,如果已经找到一个正确的路径了,换句话说已经得到结果了,其实就没必要继续DFS了,直接返回结果即可。这就是剪枝。
给一下官方的说法:剪枝,就是减小树的规模,尽早排除搜索树中不必要的分支的一种手段。
class Solution {private boolean find;public boolean exist(char[][] board, String word) {if(board == null){return false;}int m = board.length,n = board[0].length;boolean[][] visited = new boolean[m][n];find = false;for(int i = 0;i < m;i++){for(int j = 0 ;j < n;j++){backtracking(i, j, board, word, visited, 0);}}return find;}/*** i,j,board:棋盘格及当前元素的坐标* word: 要搜索的目标单词* visited:记录当前格子是否已被访问过* pos: 记录目标单词的字符索引,只有棋盘格字符和pos指向的字符一致时,才有机会继续搜索接下来的字符;如果pos已经过了目标单词的尾部了,那么便说明找到目标单词了*/public void backtracking(int i, int j, char[][] board, String word, boolean[][] visited, int pos){// 超出边界、已经访问过、已找到目标单词、棋盘格中当前字符已经和目标字符不一致了if(i < 0 || i >= board.length || j <0 || j>=board[0].length || visited[i][j] || find || board[i][j] != word.charAt(pos)){return;}if(pos == word.length()-1){find = true;return;}visited[i][j] = true;// 修改当前节点状态backtracking(i+1, j, board, word, visited, pos+1); // 遍历子节点backtracking(i-1, j, board, word, visited, pos+1);backtracking(i, j+1, board, word, visited, pos+1);backtracking(i, j-1, board, word, visited, pos+1);visited[i][j] = false; // 撤销修改}
}如果对你有帮助,麻烦双击三连一下,谢谢啦!
相关文章:

关于【网格结构】岛屿类问题的通用解法DFS(深度遍历)遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题,自己总结加上看了力扣大佬的知识总结写下本篇文章,我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题…...

【LeetCode】982. 按位与为零的三元组
982. 按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length0 < j < nums.length0 < k < num…...

Linux内核源码进程原理分析
Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task),进程的虚…...

电子技术——CMOS反相器
电子技术——CMOS反相器 在本节,我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图: 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线: 我们把 QNQ_NQN 当做是驱动源&#x…...
)
gazebo仿真轨迹规划+跟踪(不在move_base框架下)
以Tianbot为例子,开源代码如下: https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...

C. Good Subarrays(前缀和)
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组,然后我们从数组中选取一个连续的区间,这个区间满足条件:区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
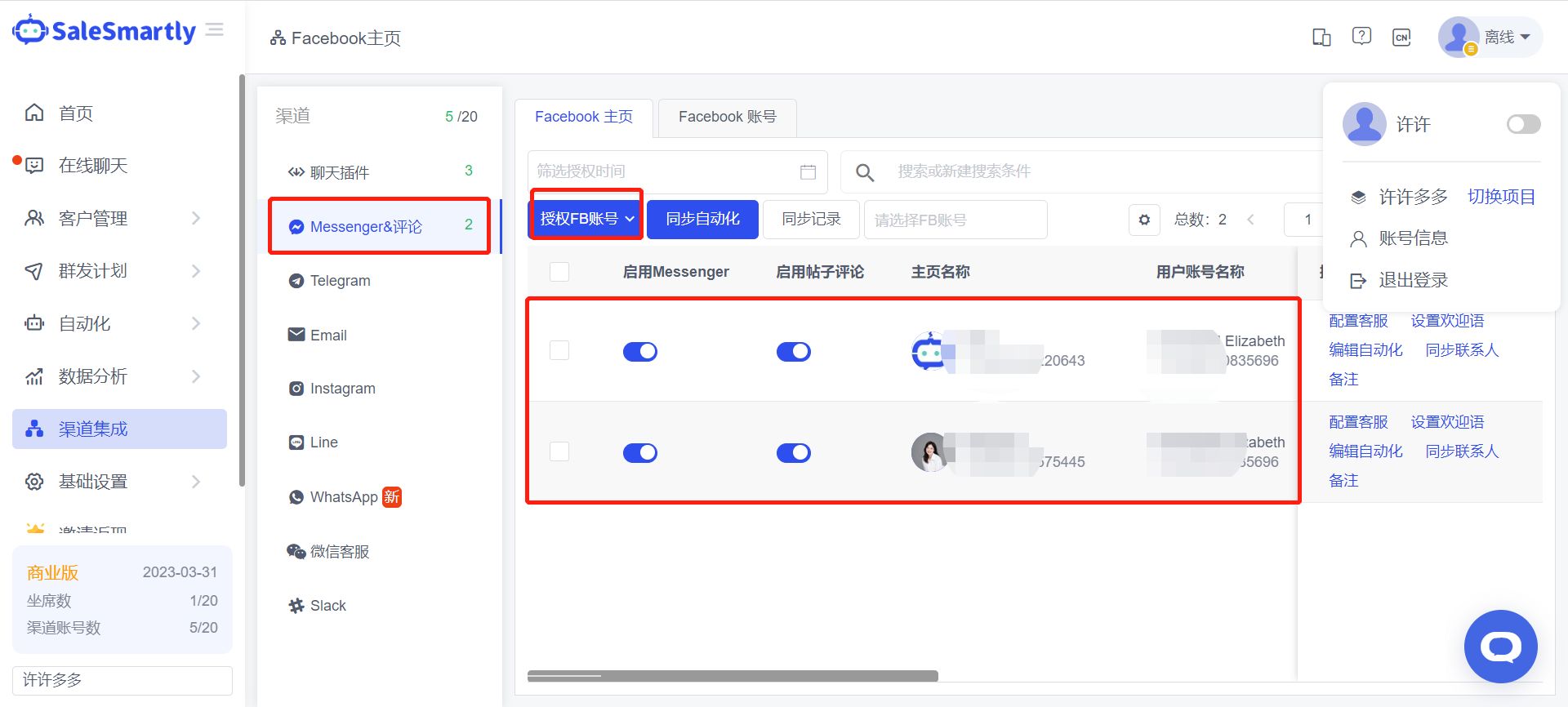
关于Facebook Messenger CRM,这里有你想要知道的一切
关于Facebook Messenger CRM,这里有你想要知道的一切!想把Facebook Messenger与你的CRM整合起来吗?这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后,我们将解释为什么你需要像SaleSmartly&a…...
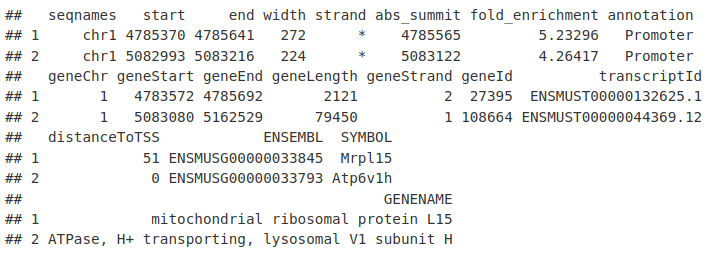
ChIP-seq 分析:数据与Peak 基因注释(10)
动动发财的小手,点个赞吧! 1. 数据 今天,我们将继续回顾我们在上一次中研究的 Myc ChIPseq。这包括用于 MEL 和 Ch12 细胞系的 Myc ChIPseq。 可在此处[1]找到 MEL 细胞系中 Myc ChIPseq 的信息和文件可在此处[2]找到 Ch12 细胞系中 Myc ChIP…...
)
《C++ Primer Plus》第18章:探讨 C++ 新标准(8)
使用大括号括起的初始化列表语法重写下述代码。重写后的代码不应使用数组 ar: class Z200 { private:int j;char ch;double z; public:Z200(int jv, char chv, zv) : j(jv), ch(chv), z(zv) {} ... };double x 8.8; std::string s "What a bracing effect!&q…...
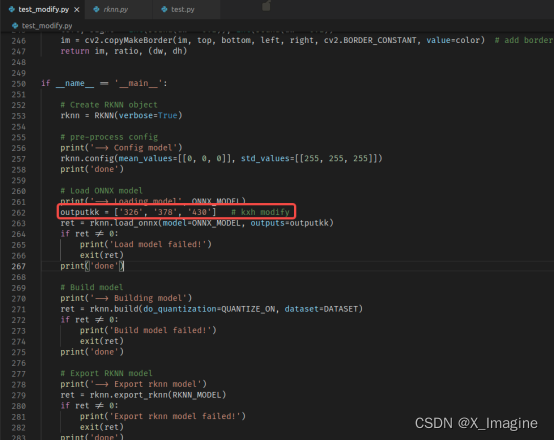
YOLO-V5 系列算法和代码解析(八)—— 模型移植
文章目录工程目标芯片参数查阅官方文档基本流程Python 版工具链安装RKNPU2的编译以及使用方法移植自己训练的模型工程目标 将自己训练的目标检测模型【YOLO-V5s】移植到瑞芯微【3566】芯片平台,使用NPU推理,最终得到正确的结果。整个过程涉及模型量化、…...

js实现复制拷贝的兼容方法
1. 定义复制拷贝的方法 在某个工具类方法中定义该方法,兼容不同浏览器处理 /*** description 拷贝的类方法*/ class CopyClass {// constructor() {}setRange(input) {return new Promise((resolve, reject) > {try {// 创建range对象const range document.c…...
学习 Python 之 Pygame 开发魂斗罗(八)
学习 Python 之 Pygame 开发魂斗罗(八)继续编写魂斗罗1. 创建敌人类2. 增加敌人移动和显示函数3. 敌人开火4. 修改主函数5. 产生敌人6. 使敌人移动继续编写魂斗罗 在上次的博客学习 Python 之 Pygame 开发魂斗罗(七)中࿰…...
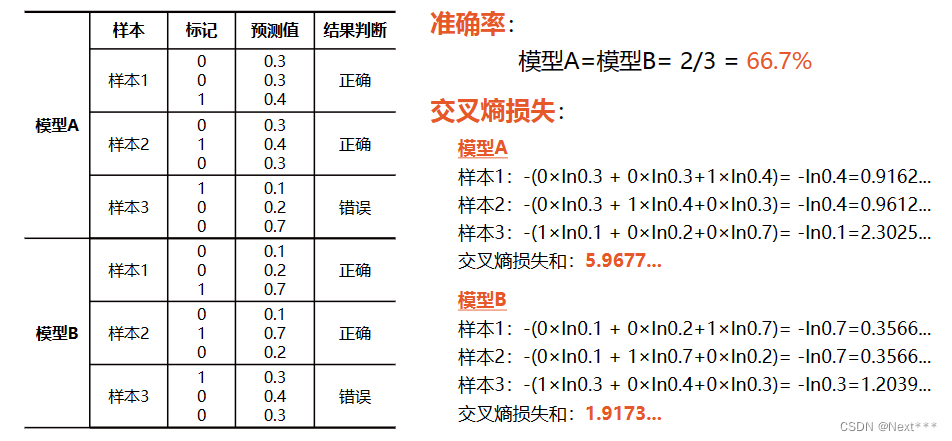
Lesson11---分类问题
11.1 逻辑回归 11.1.1 广义线性回归 课程回顾 线性回归:将自变量和因变量之间的关系,用线性模型来表示;根据已知的样本数据,对未来的、或者未知的数据进行估计 11.1.2 逻辑回归 11.1.2.1 分类问题 分类问题:垃圾…...

Python基础学习12——异常
在Python中,会使用“异常”这个十分特殊的对象来管理程序执行期间发生的错误,即报错。本文将介绍一下python基础的处理异常的方法以及一些基本的异常类型。 异常处理方法 try-except代码块 当我们编写程序时,我们可以编写一个try-except代…...

[日常练习]练习17:链表头插法、尾插法练习
[日常练习]练习17:链表头插法、尾插法练习练习17描述输入输出输入示例1输出示例1输入示例2输出示例2代码演示:总结练习17 【日常练习】 链表头插法、尾插法练习 描述 输入3 4 5 6 7 9999一串整数,9999代表结束,通过头插法新建链…...
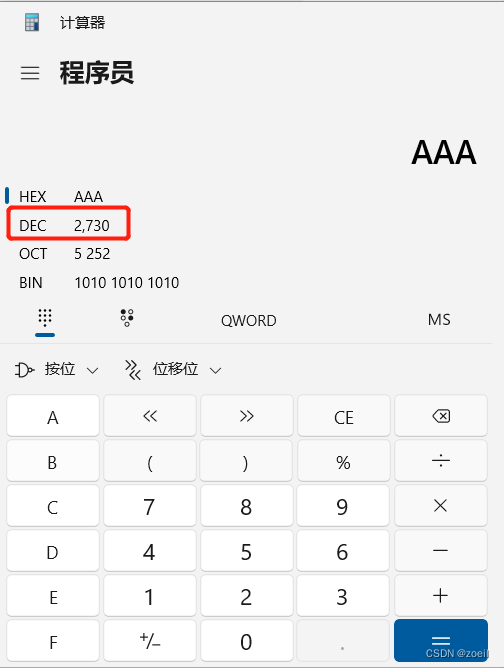
第十四届蓝桥杯模拟赛(第三期)试题与题解 C++
目录 一、填空题 (一)最小的十六进制(答案:2730) (二)Excel的列(答案:BYT) (三)相等日期(答案:70910) (四)多少种取法(答案:189)…...

关于 “宏“
起源 宏 Macro"这个词源于希腊语 “makros”,意为“大的,长的” 延伸使用 随后用于计算机领域是,在汇编语言时用于描述一大堆的汇编指令。 只要用宏指令,就是直接用的一大堆的汇编指令(有点函数的味道…...

1.2 CSS标签选择器,类选择器
CSS选择器: 根据不同的需求选出不同的标签,进行美化装饰 1. 标签选择器 标签选择器(元素选择器):用 HTML标签名作为选择器,按标签名称进行分类,为页面某一类标签指定统一的CSS样式 作用: 可以把某一类标签全部选中&…...

【Linux】进程等待 | 详解 wait/waitpid 的 status 参数
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:在上一章中我们讲解了进程创建与进程终止,本章我们开始讲解进程等待。进程等待这部分知识相较于前面还是较为复杂的࿰…...

OpenAI眼中的无线调优策略
问:无线调优策略该怎么优化无线调优是指对无线网络的各种参数进行优化,以提高网络性能和用户体验。以下是几个无线调优策略:频谱分配:通过优化频谱的分配,可以提高网络的容量和覆盖范围。在频谱分配时,需要…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

