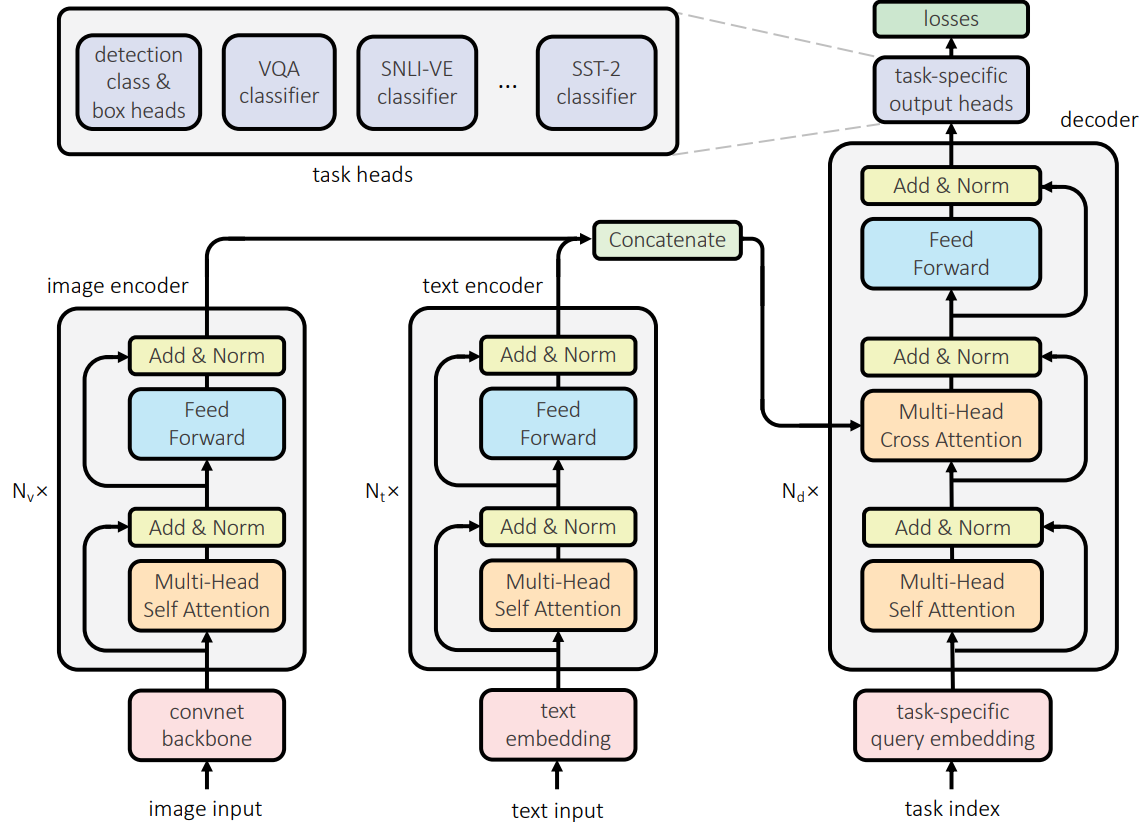
Multimodal Multitask Learning with a Unified Transformer
SNLI-VE dataset，natural language understanding tasks：MNLI，QNLI，QQP，SST-2
截止到发文时间的issue数，多吓人呐，不建议复现
相关文章：
Multimodal Multitask Learning with a Unified Transformer
SNLI-VE dataset，natural language understanding tasks：MNLI，QNLI，QQP，SST-2 截止到发文时间的issue数，多吓人呐，不建议复现...
c指针和字符数组初学者比较好的例子
本练习的主题：一个对象的指针可以修改这个对象的内容； 注：对象是指一个固定大小的内存块。 #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <string.h> #include <stdlib.h> int getMem(char **p1,int *m…...
微信原生小程序上传与识别以及监听多个checkbox事件打开pdf
1.点击上传并识别 组件样式<van-field border"{{ false }}" placeholder"请输入银行卡卡号" model:value"{{bankNo}}" label"卡号"><van-icon bindtap"handleChooseImg" slot"right-icon" name"sca…...
关于C#中Monitor的wait/pulse的理解
wait：表示释放对象上的锁并阻止当前线程，直到它重新获取该锁。 pulse：表示通知等待队列中的线程锁定对象状态的更改。 当线程调用 Wait 时，它会释放对象上的锁并进入对象的等待队列。 对象的就绪队列中的下一个线程 (如果有一个…...
LeetCode 2894. 分类求和并作差
给你两个正整数 n 和 m 。 现定义两个整数 num1 和 num2 ，如下所示： num1：范围 [1, n] 内所有 无法被 m 整除 的整数之和。 num2：范围 [1, n] 内所有 能够被 m 整除 的整数之和。 返回整数 num1 - num2 。 示例 1： …...
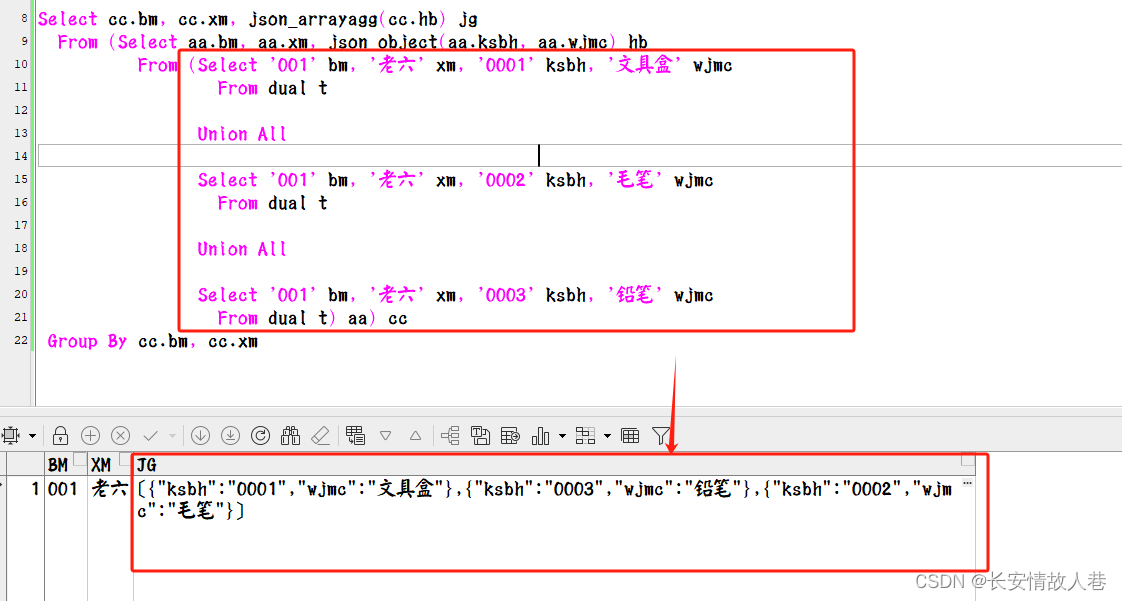
PLSQL 把多个字段转为json格式
PLSQL 把多个字段转为json格式 sql Select cc.bm, cc.xm, json_arrayagg(cc.hb) jgFrom (Select aa.bm, aa.xm, json_object(aa.ksbh, aa.wjmc) hbFrom (Select 001 bm, 老六 xm, 0001 ksbh, 文具盒 wjmcFrom dual tUnion AllSelect 001 bm, 老六 xm, 0002 ksbh, 毛笔 wjmcFr…...
国内环境 GitHub 拉取仓库速度慢的缓解方案
第一步： 浏览器打开如下两个网址，找到对应 IP 地址： GitHub.com - GitHub: Lets build from here GitHubgithub.global.ssl.fastly.net 假设对应 IP 地址分别为 140.82.xx.xxx 和 199.232.yy.yyy 第二步： 编辑 hosts 文件 sud…...
设计模式⑥ ：访问数据结构
文章目录 一、前言二、Visitor 模式1. 介绍2. 应用3. 总结 三、Chain of Responsibility 模式1. 介绍2. 应用3. 总结 参考内容 一、前言 有时候不想动脑子，就懒得看源码又不像浪费时间所以会看看书，但是又记不住，所以决定开始写"抄书&q…...
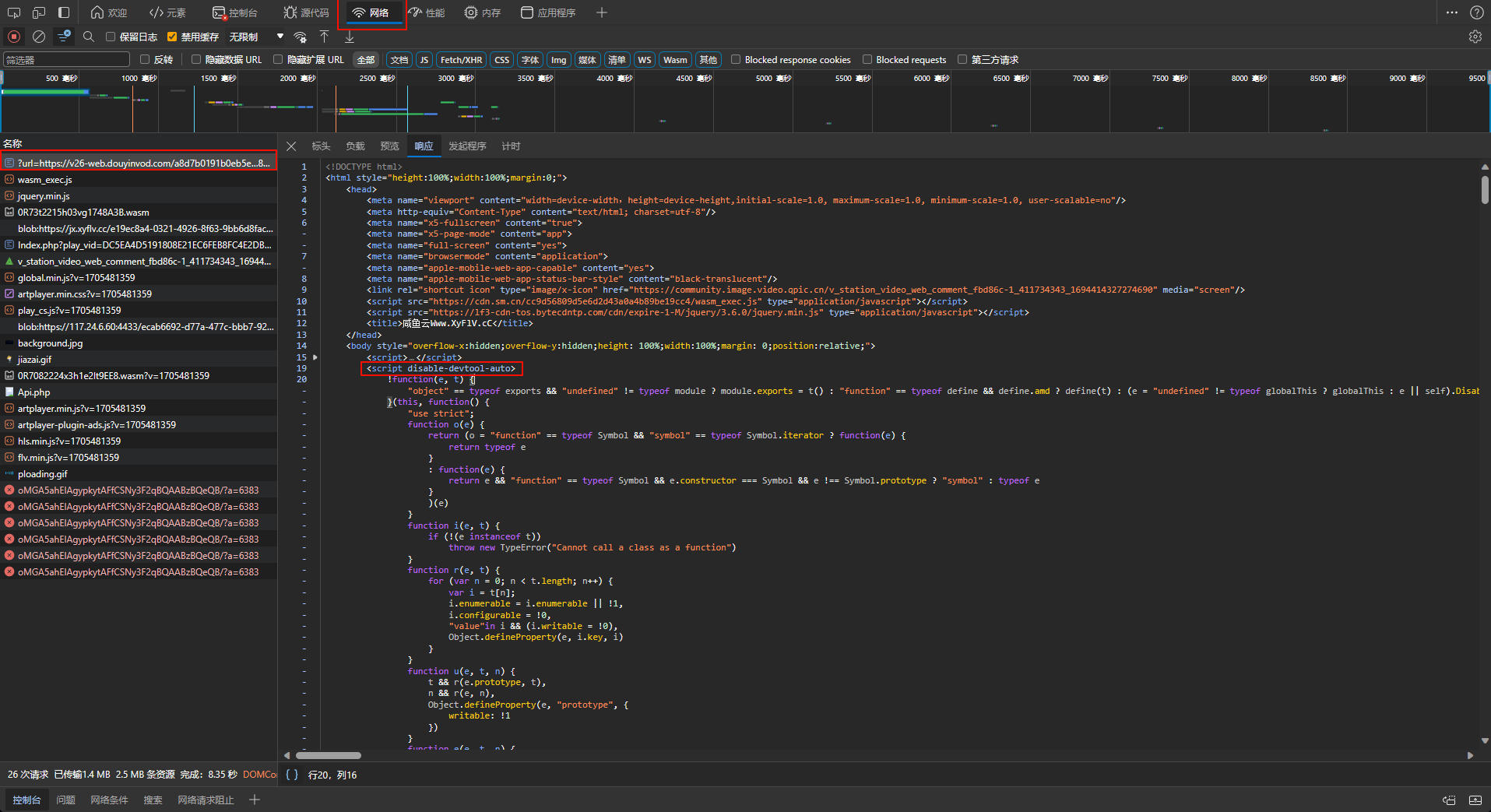
无法打开浏览器开发者工具的可能解决方法
网页地址: https://jx.xyflv.cc/?url视频地址url 我在抖音里面抓了一个视频地址, 获取到响应的json数据, 找到里面的视频地址信息 这个网站很好用: https://www.jsont.run/ 可以使用js语法对json对象操作, 找到所有视频的url地址 打开网页: https://jx.xyflv.cc/?urlhttps:…...
Android ANR 总结
工作之余，对之前学习到的和结合自己项目过程中的遇到的问题经验做一些总结，下面讲一讲Android开发过程中遇到的ANR的问题，做一下整理 一、概述 解决ANR一直是Android 开发者需要掌握的重要技巧，一般从三个方面着手。 开发阶段&a…...
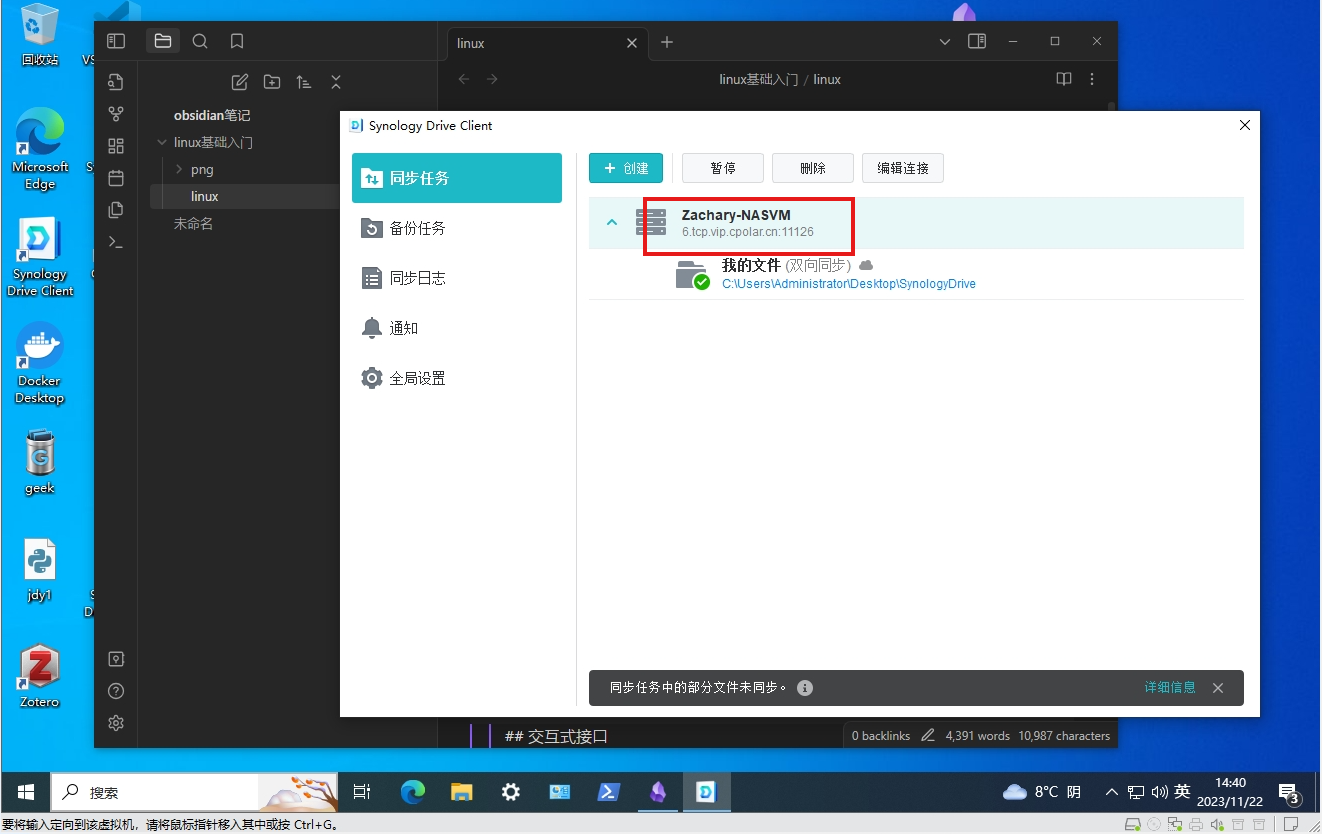
群晖Drive搭建云同步服务器结合内网穿透实现Obsidian笔记文件远程多端同步
文章目录 一、简介软件特色演示： 二、使用免费群晖虚拟机搭建群晖Synology Drive服务，实现局域网同步1 安装并设置Synology Drive套件2 局域网内同步文件测试 三、内网穿透群晖Synology Drive，实现异地多端同步Windows 安装 Cpolar步骤&#…...
Flutter中的图片查看器：使用photo_view库
在移动应用开发中，图片查看器是一个常见的需求。Flutter提供了许多库来简化这一过程，其中photo_view库是一个强大而灵活的选择。本文将介绍photo_view库的基本概念以及如何在Flutter应用中使用它来实现漂亮的图片查看体验。 1. 什么是photo_view库&…...
软件测试|使用Python轻松裁剪视频
简介 裁剪视频是在视频编辑和处理中常见的任务之一，Python提供了多种库和工具，可以用来裁剪视频。在本文中，我们将详细讨论如何使用Python来裁剪视频，并提供示例代码。 步骤1：环境准备 首先，我们要安装必…...
计算机网络——运输层（1）暨小程送书
计算机网络——运输层（1）暨小程送书 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU) 运输层概述两个主要协议运输层和网络层的关系网络层运输层总结 多路复用与多路分解多路复用多路分解不同的技术实现时分复用（TDM）频分复…...
中国互联网的早期形态
1 大约是从 1991 年开始，国内开始了第一个 BBS 站——北京长城站，经过长时间发展，直到 1995 年，随着计算机及其外设的大幅降价，BBS 才逐渐被部分人们所认识。少数玩 BBS 站的“极客”站长， 基于个人关系&am…...
机场数据治理系列介绍（3）：从数据到资产认定过程要搞懂的一些概念
目录 一、从数据到资产的基本背景 1、国家政策方面的梳理 2、地方政府的摸索实践梳理 二、数据资产化相关概念 1、数据 2、资产 3.、数据资产 4、数据资产入表 5、数据资源VS数据资产 三、关于《企业数据资源相关会计处理暂行规定》的相关解读 1、《暂行规定》不涉及…...
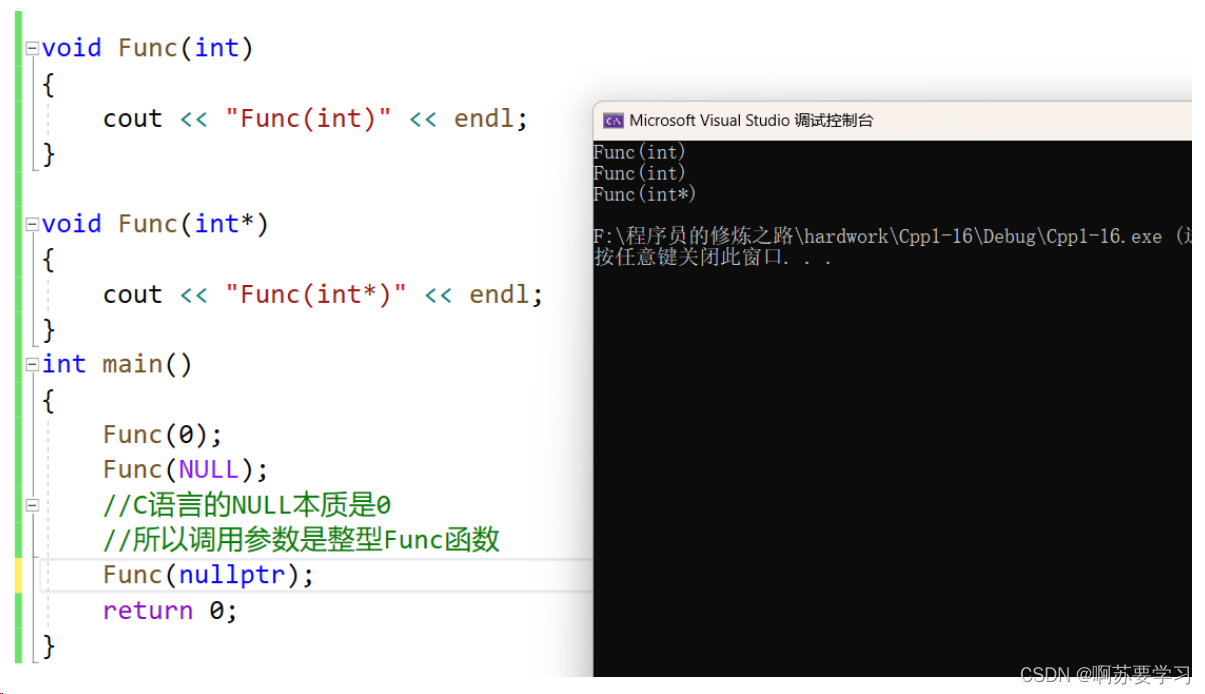
《C++入门篇》——弥补C不足
文章目录 前言一.命名空间二.缺省参数三.函数重载四.引用4.1引用做参数4.2引用做返回值 五.内联函数六.小语法6.1auto6.2范围for6.3空指针 前言 C是业内一门久负盛名的计算机语言，从C语言发展起来的它，不仅支持C语言的语法，还新添加了面向对…...
要在Linux上安装Docker Compose和nginx
一、要在Linux上安装Docker Compose，您可以按照以下步骤进行操作： 确保您的Linux系统已经安装了Docker。您可以通过运行以下命令来检查Docker是否已经安装： docker --version如果Docker未安装，请先安装Docker。 下载Docker Compo…...
zsh插件之gitignore安装使用教程
安装 zsh 插件管理工具 首先，确保你已经安装了 zsh，然后安装 Oh My Zsh，这是一个流行的 zsh 配置框架。在终端运行以下命令安装 Oh My Zsh： bashCopy code sh -c "$(curl -fsSL https://raw.github.com/ohmyzsh/ohmyzsh/ma…...
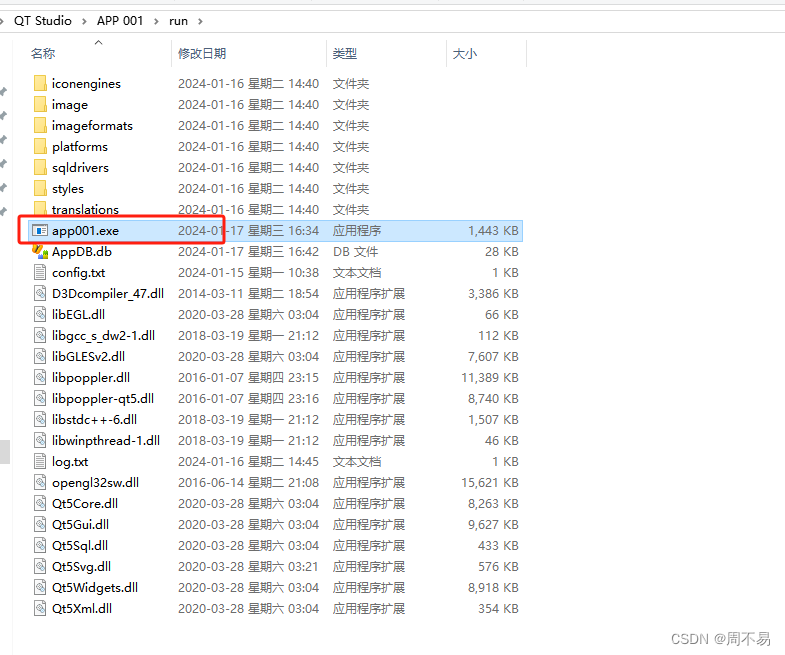
十二、Qt 操作PDF文件(2)
一、在《十、Qt 操作PDF文件-CSDN博客》中我们用Poppler类库打开了PDF文件，并显示到窗体上，但只能显示一页，功能还没完善，在本章节中，加入了： 通过选择框选择PDF文件并打开，默认打开第一页。通…...
生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式，可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
python打卡day49
知识点回顾： 通道注意力模块复习空间注意力模块CBAM的定义 作业：尝试对今天的模型检查参数数目，并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略，并且实现了基本的选区操作，还调研了自绘选区的实现。那么相对的，我们还需要设计编辑器的选区表达，也可以称为模型选区。编辑器中应用变更时的操作范围，就是以模型选区为基准来…...
leetcodeSQL解题：3564. 季节性销售分析
leetcodeSQL解题：3564. 季节性销售分析 题目： 表：sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令，在Linux上安装软件，以及如何在Linux上部署一个单体项目，大多数同学都会有相同的感受，那就是麻烦。 核心体现在三点： 命令太多了，记不住 软件安装包名字复杂&…...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer （1）资源 论文&a…...
NXP S32K146 T-Box 携手 SD NAND（贴片式TF卡）：驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中，车辆不再仅仅是传统的交通工具，而是逐步演变为高度智能的移动终端。这一转变的核心支撑，来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒（T-Box）方案：NXP S32K146 与…...
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...
【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中（图1）： mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...