【测绘程序设计】——空间直角坐标转换
相关文章:

【测绘程序设计】——空间直角坐标转换
测绘工程中经常遇到空间直角坐标转换——比如,北京54(或西安80)空间直角坐标转换成CGCS2000(或WGS-84)空间直角坐标,常用转换模型包括:①布尔沙模型(国家级及省级范围);②莫洛坚斯基模型(省级以下范围);③三维四参数(小于22局部区域) 等。 本文分享了基于布…...
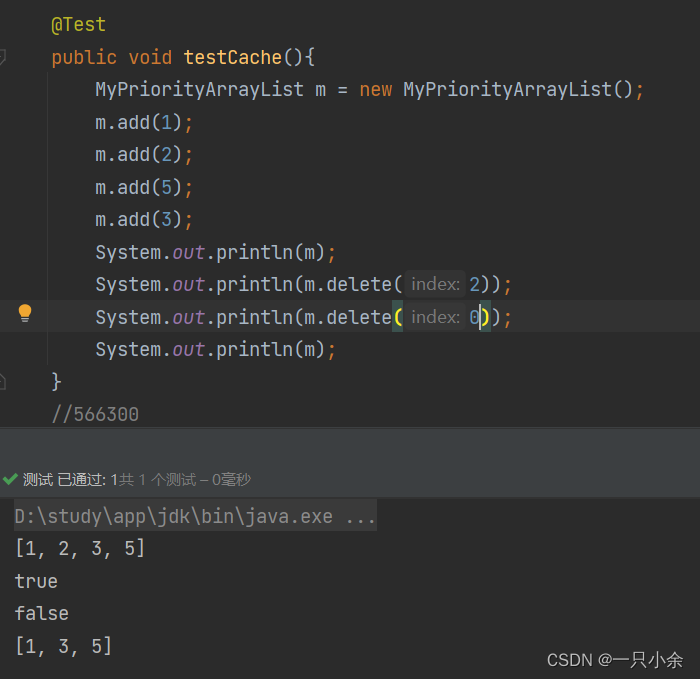
数组--java--动态数组--有序数组--底层
java数组基础--java中的数组创建数组空间占用初始化数组访问元素插入查找删除元素动态数组扩容插入和添加重写toString删除二维数组二维数组注意点有序数组实现测试写在开头: 这篇文章包括数组的基础、一点底层的内容和一些稍微深入的东西。 作为第一个深入学习的数…...

Linux下使用C语言实现简单的聊天室程序
本文章介绍一种基于Linux使用C语言实现简单的局域网聊天室程序的方法,支持消息群发,历史数据查询,好友列表查看,好友上线下线提醒等功能。聊天界面如下图所示:下面将按步骤介绍该系统的设计实现,首先在linu…...

【数学】任意一个正整数n最多只有一个质因数大于根号n,怎么证明?
定理 任意一个正整数n最多只有一个大于n\sqrt{n}n的质因子,并且该大于n\sqrt{n}n质因子的幂次是1。 证明(反证法) 证明:最多只有一个大于n\sqrt{n}n的质因子 假设n存在两个大于n\sqrt{n}n的质因子,分别为p…...

【ES6】var let const 之面试题系列
关于 var、let、const 是前端开发人员经常用到的关键字,也是经典的面试题,接下来就站在面试题的角度来看待它们之间的区别。 一、区别 1. var 声明的范围是函数作用域,let 和 const 声明的范围是块作用域,块作用域是函数作用域的…...
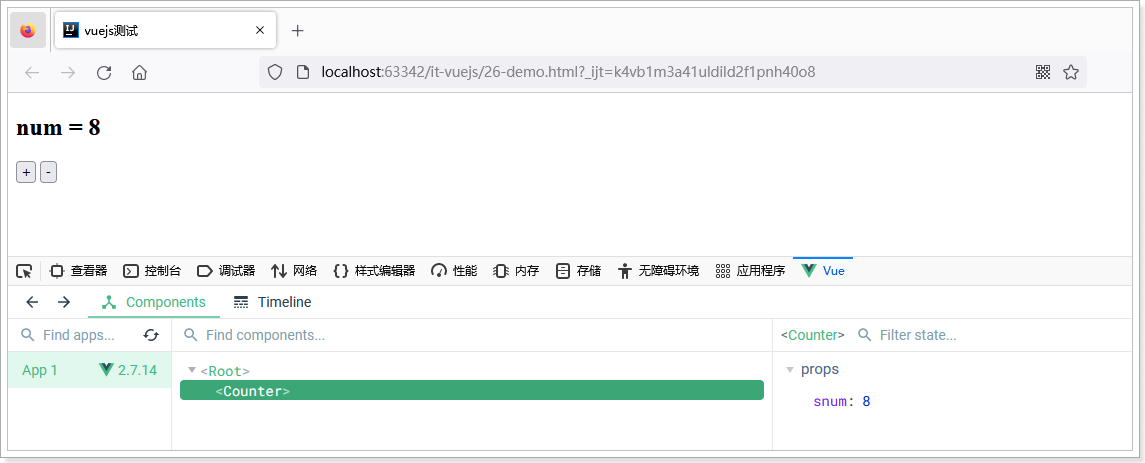
Vue基础入门讲义(四)-组件化
文章目录1.引言2.定义全局组件3.组件的复用4.局部注册5.组件通信5.1.父向子传递props5.2.传递复杂数据5.3.子向父的通信1.引言 在大型应用开发的时候,页面可以划分成很多部分。往往不同的页面,也会有相同的部分。例如可能会有相同的头部导航。 但是如果…...

Android onLayout布局流程解析
组件布局流程结论 1.)layout流程始于ViewRootImpl的performLayout()方法,该方法会调用根View(DecorView)的layout()方法进行布局,因为DecorView是ViewGroup(FrameLayout),所以layout流程来到了ViewGroup(其…...
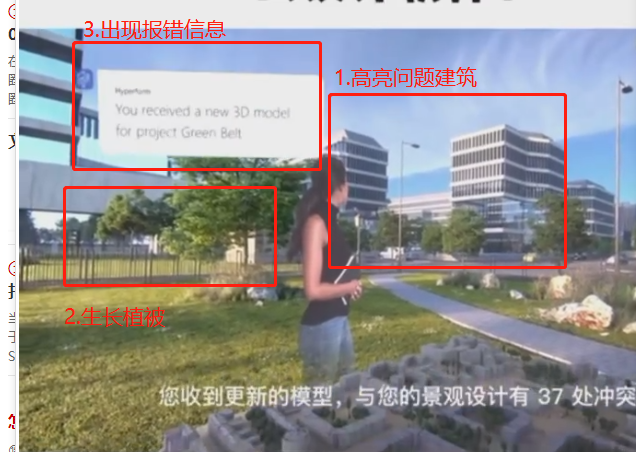
浅分析BIG-建筑展示系统
一、主页(主要界面)重点疑点(需要解决)1.云平台实时同步。是否可以电脑与hololens2同步或链接?并可以传输信息提醒?一级界面(启动界面)1.交互式启动激活效果(触发按钮旋转…...

模电基础(1) 半导体基础知识
基本内容: 1.本征半导体的基本介绍结构; 2.杂质半导体; 3.PN结的形成; 4.PN结的性质。 1.本征半导体 半导体:导电性能介于绝缘体和导体之间的物质。 本征半导体是纯净的晶体结构的半导体。 纯净→无杂质晶体结构→稳…...

阅读笔记:TF - IDF 原理
今天查阅 TF-IDF 资料,发现百度百科里面提供了一个例子,解释的很清楚,记下来备用。 原文链接:https://baike.baidu.com/item/tf-idf/8816134?fraladdin 例子:在某个一共有一千词的网页中 “原子能”、“的” 和 “应…...

【C语言】float 关键字
🚩write in front🚩 🔎大家好,我是謓泽,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🏅2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4…...
)
Linux 网络编程(实现多路IO转接服务器)
1.select函数实现多路IO转接服务器select函数原型:包含在头文件<sys/time.h>,<sys/types.h>和<unistd.h>int select(int nfds, fd_set *readfds, fd_set *writefds,fd_set *exceptfds, struct timeval *timeout);作用:确定…...
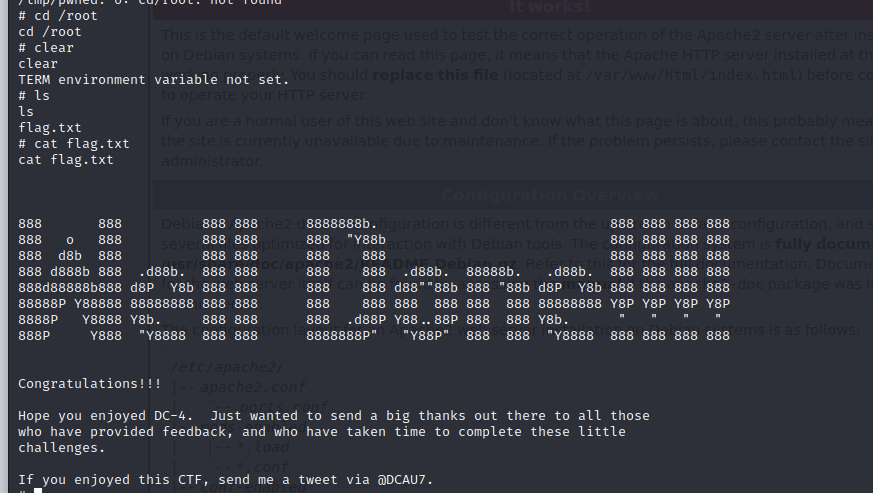
DC-4 靶场学习
信息搜集: 首先获取靶场ip,和之前一样。 arp-scan -l nmap -sP 192.168.28.0/24然后访问。 发现需要登录。 漏洞分析: 直接用bp爆破,爆破出来密码为happy,登录。 发现执行了命令,抓包。 修改命令可以执行ÿ…...
QML组件
一个QML文件定义了一个独立的、顶级的QML组件。 一个QML组件就是一个模板,被QML运行环境解释来创建一个带有一些预定义行为的对象。 一个独立的QML组件可以运行多次来禅城多个对象,每个对象都可以称为该组件的实例。 例子: 在项目中添加一…...

canvas 学习指南
canvas 学习指南 创建一个 canvas <! DOCTYPE html><html xmlns"http://www.w3.org/1999/xhtml"><head><title></title><meta charset"utf-8" /><script type"text/javascript">window.onload fun…...

【华为OD机试2023】开心消消乐 C++
【华为OD机试2023】开心消消乐 C++ 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收输入、print/cou…...

学历?能力?
一个面试官愿意看一张有形的总结报告,还是愿意相信看不到的人品?...
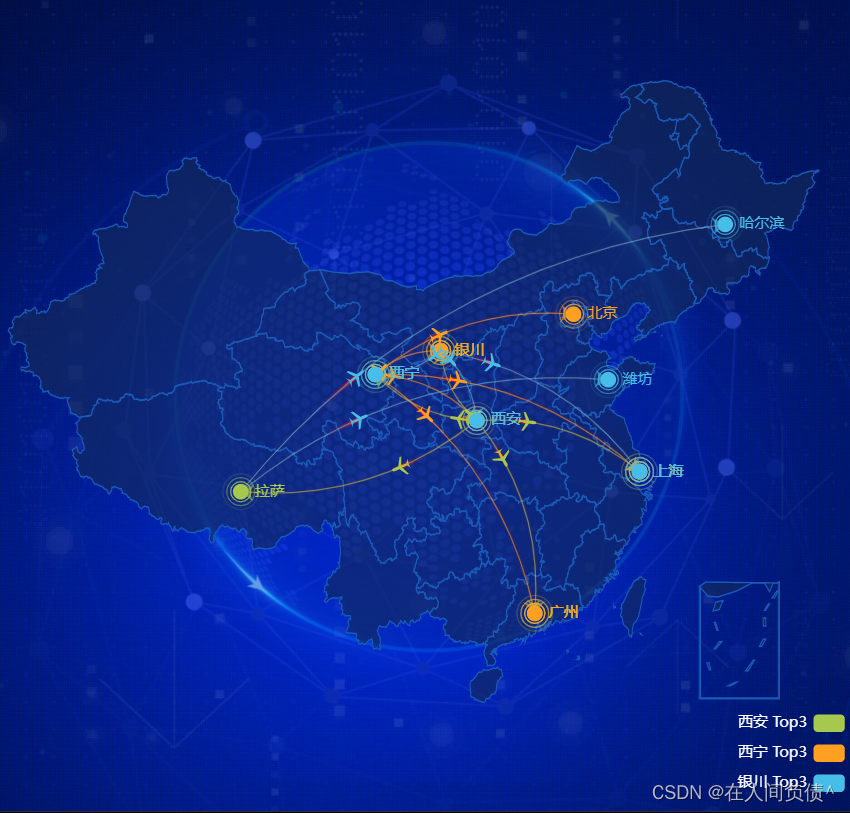
使用ECharts打造一个数据可视化面板
使用ECharts打造一个数据可视化面板1. 使用技术2. 案例适配方案3. 基础设置4. header 布局5. mainbox 主体模块6. 公共面板模块 panel7. 柱形图 bar 模块(布局)8. 中间布局9. ECharts 介绍10. ECharts 体验11. ECharts 基础配置12. 柱状图图表࿰…...

【论文简述】PVSNet: Pixelwise Visibility-Aware Multi-ViewStereo Network(arxiv 2020)
一、论文简述 1. 第一作者:Qingshan Xu 2. 发表年份:2020 3. 发表期刊:arxiv 4. 关键词:MVS、3D重建、可见性、代价体、训练策略 5. 探索动机:ETH3D基准测试提供的图像包含强烈的视图变化,这就要求MVS…...

CSS隐藏元素的几种方式以及display、visibility、opacity的区别
CSS隐藏元素的方式首先最通用且最易想到的方法肯定是display、visibility和opacity这三种了display:none设置元素不可见并且连盒模型也不生成,一般用于不占空间的隐藏元素。display属性规定元素应该生成的框的类型,当其值为“none”时可以规定元素不生成…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
