代码随想录算法训练营第三十八天|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
题目:理论基础
文章链接:代码随想录
视频链接:动态规划理论基础
动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
题目:509. 斐波那契数
文章链接:代码随想录
视频链接:LeetCode:509.斐波那契数
题目链接:力扣题目链接
图释:
class Solution {
public:// 确定dp数组(dp table)以及下标的含义 vector<int> dp, dp[i]表示第n哥斐波那契数 // 确定递推公式 dp[i]=dp[i-1]+dp[i-2]// dp数组如何初始化 dp[0]=1, dp[1]=1// 确定遍历顺序 从前往后// 举例推导dp数组 int fib(int n) {if(n<=0)return 0;if(n==1) return 1;vector<int> dp(n+1);dp[0]=0;dp[1]=1;for(int i=2; i<=n; i++){//从2开始,直到第n个数dp[i]= dp[i-1]+dp[i-2];}return dp[n];}
};class Solution {
public:int traversal(int n){// 终止条件if(n==1) return 1;if(n==0) return 0;// 递归return traversal(n-1)+traversal(n-2);} int fib(int n) { return traversal(n);}
};再精简
class Solution {
public:int fib(int n) { // 终止条件if(n==1) return 1;if(n==0) return 0;return fib(n-1)+fib(n-2);}
};题目:70. 爬楼梯
文章链接:代码随想录
视频链接:LeetCode:70.爬楼梯
题目链接:力扣题目链接
图释:
class Solution {
public:// 确定dp数组(dp table)以及下标的含义 vector<int> dp, dp[i]表示达到第n层楼梯需要的方法 // 确定递推公式 dp[i]=dp[i-1]+dp[i-2]// dp数组如何初始化 dp[1]=1, dp[2]=2// 确定遍历顺序 从前往后// 举例推导dp数组 // 题目中要求的每次可以爬1或者2个台阶,也就是说,最终到达n阶台阶有两种方式,// 一个是爬1阶台阶到达(对应的是从n-1阶台阶开始)// 另一个就是爬2阶台阶到达(对应的是从n-2阶台阶开始爬),// 而爬n-1阶和n-2阶台阶的方法有dp[n-1],dp[n-2]个// 所以最终爬n阶台阶的方法种类就是dp[n-1]+dp[n-2]int climbStairs(int n) {if(n==1) return 1;if(n==2) return 2;vector<int> dp(n+1);dp[1]=1;dp[2]=2;for(int i=3; i<=n; i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
};class Solution {
public:int climbStairs(int n) {if(n==1) return 1;if(n==2) return 2;return climbStairs(n-1)+climbStairs(n-2);}
}; //超时
题目:746. 使用最小花费爬楼梯
文章链接:代码随想录
视频链接:LeetCode:746.使用最小花费爬楼梯
题目链接:力扣题目链接
图释:
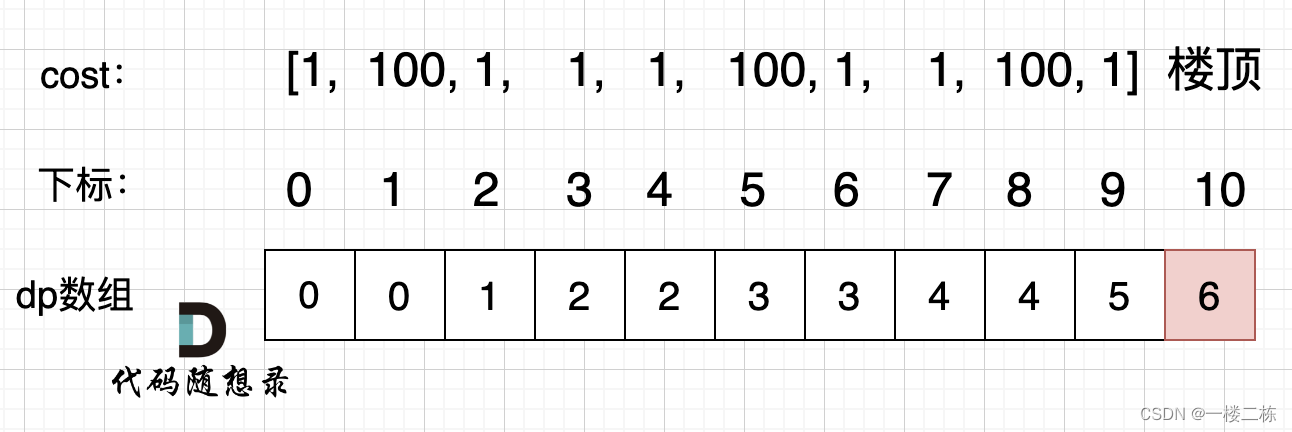
class Solution {
public:// 确定dp数组(dp table)以及下标的含义 vector<int> dp, dp[i]表示爬到第n层台阶的最低花费// 确定递推公式 dp[i]= min(dp[i-1]+cost[i-1], dp[i-2]+cost[i+2]) 可以选择从前一个台阶或者前两个台阶爬上来 // dp数组如何初始化 dp[0]=0, dp[1]=0 题目说了,可以选择从0或者1台阶出发,也就是dp[i]到这两个台阶的最低花费为0// 确定遍历顺序 从前往后// 举例推导dp数组 int minCostClimbingStairs(vector<int>& cost) {if(cost.size()==0 || cost.size()==1) return 0;vector<int> dp(cost.size()+1);dp[0]=dp[1]=0;for(int i=2; i<=cost.size(); i++){ // 顶楼表示为dp[n] dp[i]= min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};相关文章:

代码随想录算法训练营第三十八天|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
题目:理论基础 文章链接:代码随想录 视频链接:动态规划理论基础 动态规划五部曲: 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 题目:509. 斐…...
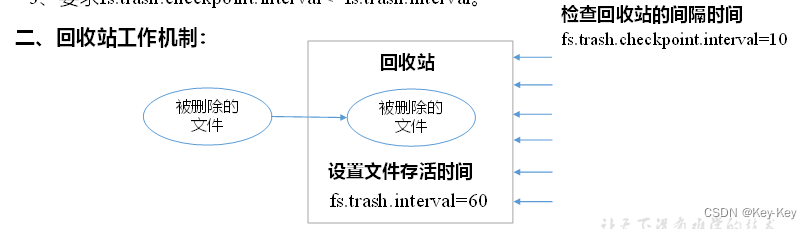
大数据开发之Hadoop(优化新特征)
第 1 章:HDFS-故障排除 注意:采用三台服务器即可,恢复到Yarn开始的服务器快照。 1.1 集群安全模块 1、安全模式:文件系统只接收读数据请求,而不接收删除、修改等变更请求 2、进入安全模式场景 1)NameNod…...

在使用go语言开发的时候,程序启动后如何获取程序pid
在Go语言中,标准库并没有直接提供获取进程ID(PID)的函数。通常,你可以使用os包和syscall包来调用底层的操作系统函数来获取PID。 以下是一个获取程序PID的示例代码: package mainimport ("fmt""os&qu…...
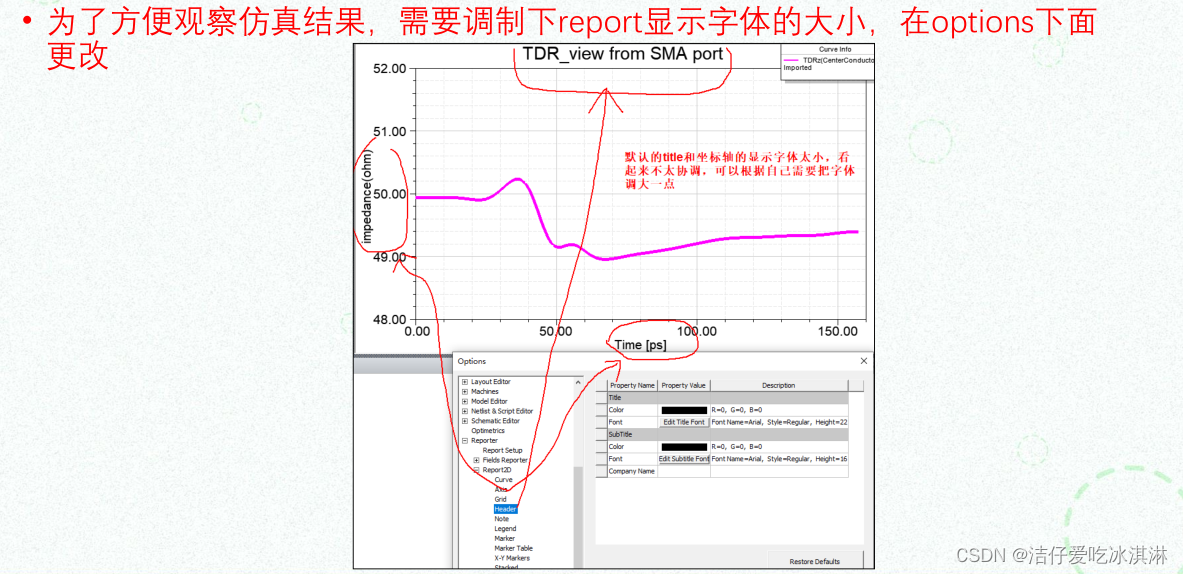
HFSS笔记/信号完整性分析(二)——软件仿真设置大全
文章目录 1、多核运算设置1.1 如何设置1.2 如何查看自己电脑的core呢?1.3 查看求解的频点 2、求解模式设置Driven Terminal vs Driven modal 3、Design settings4、自适应网格划分5、更改字体设置 仅做笔记整理与分享。 1、多核运算设置 多核运算只对扫频才有效果&…...

mysql主从报错:Last_IO_Error: Error connecting to source解决方法
目录 报错 处理方法 1.从库停止同步 2.主库修改my.cnf 生效配置default-authentication-pluginmysql_native_password 3.重启服务重新创建复制用户 4.重新同步 5.测试主从 报错 Last_IO_Error: Error connecting to source repl_user192.168.213.15:3306. This was atte…...

AOI与AVI:在视觉检测中的不同点和相似点
AOI(关注区域)和AVI(视觉感兴趣区域)是视觉检测中常用的两个概念,主要用于识别和分析图像或视频中的特定区域。虽然这两个概念都涉及到注视行为和注意力分配,但它们在定义和实际应用等方面有一些差异。 AOI…...

Python爬虫 - 网易云音乐下载
爬取网易云音乐实战,仅供学习,不可商用,出现问题,概不负责! 分为爬取网易云歌单和排行榜单两部分。 因为网页中,只能显示出歌单的前20首歌曲,所以仅支持下载前20首歌曲(非VIP音乐&…...
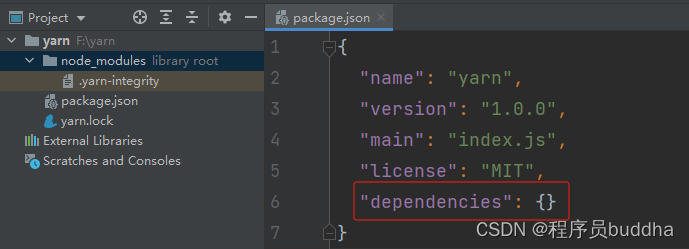
yarn包管理器在添加、更新、删除模块时,在项目中是如何体现的
技术很久不用,就变得生疏起来。对npm深受其害,决定对yarn再整理一遍。 yarn包管理器 介绍安装yarn帮助信息最常用命令 介绍 yarn官网:https://yarn.bootcss.com,学任何技术的最新知识,都可以通过其对应的网站了解。无…...
)
React实现Intro效果(基础简单)
下载:利用Intro.js实现简单的新手引导 npm install intro.js --save yarn add intro.js 第一步:在我们需要引导的页面引入 import introJs from intro.js; import intro.js/introjs.css; //css是下载成功后就有的 第二步:在组件页面 c…...

HBuilderx发布苹果的包需要注意什么
在HBuilderX中发布苹果的包,需要注意以下几点: 开发者账号注册:在发布应用到App Store之前,需要先注册一个苹果开发者账号。注册过程较为繁琐,需要提供个人信息并支付年费。应用标识和证书:在发布iOS应用之…...
烟火检测/周界入侵/视频智能识别AI智能分析网关V4如何配置ONVIF摄像机接入
AI边缘计算智能分析网关V4性能高、功耗低、检测速度快,易安装、易维护,硬件内置了近40种AI算法模型,支持对接入的视频图像进行人、车、物、行为等实时检测分析,上报识别结果,并能进行语音告警播放。算法可按需组合、按…...

C++ 内联函数
C 内联函数是通常与类一起使用。如果一个函数是内联的,那么在编译时,编译器会把该函数的代码副本放置在每个调用该函数的地方。 对内联函数进行任何修改,都需要重新编译函数的所有客户端,因为编译器需要重新更换一次所有的代码&a…...

微信小程序带参数分享界面、打开界面加载分享内容
分享功能是微信小程序常用功能之一,带参分享和加载可以让分享对象打开界面时看到和分享内容。 带参分享 用户点击微信小程序右上角自带分享,或者点击自定义分享按钮进行分享时,可在onShareAppMessage函数定义分享行为。 分享界面路径可带参…...

中小企业选择CRM系统有哪些注意事项?如何高效实施CRM
阅读本文,你将了解:一、中小型企业对CRM系统的主要需求;二、CRM系统实施策略和优秀实践。 在快速变化的商业环境中,中小型企业面临着独特的挑战:如何在有限的资源下高效地管理客户关系、提升销售效率,保持…...
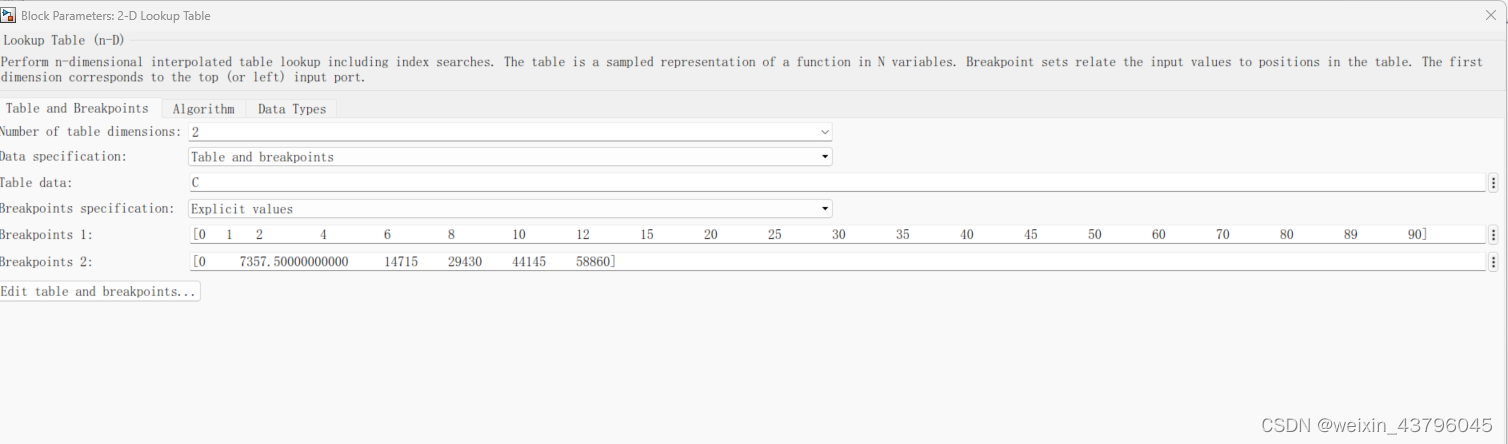
轮胎侧偏刚度线性插值方法
一、trucksim取数据 步骤一 步骤二 二、数据导入到matlab中 利用simulink的look up table模块 1是侧偏角;2是垂直载荷;输出是侧向力。 侧向力除以侧偏角就是实时的侧偏刚度。...

前端JS代码中Object类型数据的相关知识
获取Object类型数据的方式有两种: 方括号获取:Object["arg1"]点获取:Object.arg1 前端遍历Object类型数据的方式 遍历JavaScript中的对象有几种方法,包括使用for…in循环、Object.keys()方法、Object.values()方法和…...
vue基于Spring Boot共享单车租赁报修信息系统
共享单车信息系统分为二个部分,即管理员和用户。该系统是根据用户的实际需求开发的,贴近生活。从管理员处获得的指定账号和密码可用于进入系统和使用相关的系统应用程序。管理员拥有最大的权限,其次是用户。管理员一般负责整个系统的运行维护…...
CentOS 6.10 安装图解
特特特别的说明 CentOS发行版已经不再适合应用于生产环境,客观条件不得不用的话,优选7.9版本,8.5版本次之,最次6.10版本(比如说Oracle 11GR2就建议在6版本上部署)! 引导和开始安装 选择倒计时结…...

Web自动化测试中的接口测试
1、背景 1.1 Web程序中的接口 1.1.1 典型的Web设计架构 web是实现了基于网络通信的浏览器客户端与远程服务器进行交互的应用,通常包括两部分:web服务器和web客户端。web客户端的应用有html,JavaScript,ajax,flash等&am…...

轻松识别Midjourney等AI生成图片,开源GenImage
AIGC时代,人人都可以使用Midjourney、Stable Diffusion等AI产品生成高质量图片,其逼真程度肉眼难以区分真假。这种虚假照片有时会对社会产生不良影响,例如,生成公众人物不雅图片用于散播谣言;合成虚假图片用于金融欺诈…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
