C语言中的浮点数存储
首先明确一个概念:C语言中整形是按照二进制存储在内存中,浮点型是按科学计数法存储在内存中(本质上存储的还是二进制数据0和1)。
如果没看懂这句话,没关系!看完以下正文,你就会豁然开朗!并且预先提出两个问题:
1)为什么浮点型不能执行位运算?
2)浮点型数据转换为整形数据时,编译器内部做了什么样的处理?
接下来,讲解C语言中浮点型数存储的规则:
c语言中的浮点型有如下几种 (float ,double ,longdouble),因为不同系统平台下数据类型的长度会不一样,这里我们统一在32位GCC编译器下, float=4Byte,double=8个Byte
先定义
float num_1=10.5f; /* 这里有个小知识点,很多编译器中,如果10.5后面不加f(小写),会默认为存储为double类型*/
double num_2 = 11.5
根据国际电器和电子工程协会,标准IEEE754规定,浮点数可以按照以下规则存储
(-1)^S*M*2^E
可以将上述公式分为两部分来看(-1)^S是确定数字是整数还是负数。M*2^E确定的数字绝对值的大小。
这里的M必须是二进制数。
S必须是整数1,或整数0
E也必须是>=0的整数
结合图形来看:

C语言存储浮点型数据float时,会将内存分为三个区域。结合实例我们来看
float num_1=10.5,先转换为IEEE754格式,首先该数为正数故s=0;(-1)^0=0,符号位=0,表示正数。
第1步:在把10.5转换为科学计数法 1.05*10^1,
第2步:再把10.5二进制格式,其中M要为二进制数据,dec(10.5)=bin(1010.1)
第3步:二进制写成科学计数法10.5=1010.1*2^0 = 1.0101*2^3。
10.5为正数于是 31符号位=0、E=3 =0000 0011 。有效数字M=1.0101。但是如果你按上述来写,肯定是错误的。浮点数存储时,还要遵守一定的转换方式:转换规则如下(也是很重要的一个知识点)
(规则1)1<=M<2。IEEE 754规定 M只存储小数部分,于是10.5只会存储0101,系统会默认最高位为1(。
(规则2)而E,存储时:
float类型数据,存储值=E+127.
double类型数据,存储值=E+1023.
首先得明确是一个无符号数,10.5=1.0101*2^3,E=3,二进制表示为 0000 0011。IEEE754规定了。对于8bit长度的float类型。e需要加上127,在此得到的数,再存储到内存中去。3+127=129=1000 0010。double类型,应该加上1023。至于为什么,后面细说。

于是10.5的正确格式应该是上图所示的格式。
至于E为什么要+127(float)+1023(double)。
问:0.5该如何存储?
转换为二进制科学计数法1*2^-1。如果我们E不做处理。
将会有如下问题,s=0,没有问题,E=-1,E是无符号数,不能显示为-1。M存储的是小数部分,全部存储为0。
故为了解决E无法表示负数的问题,才引入了E+127(Float),和E+1023(double)。为了描述方便,下面统一以float类型为例,当E存储值<127时,认定E为负数,如E存储值为125,则E的实际值为-2。当E的存储值>127时,E的真实值为正数,130=3。以此类推。。。。
故,本质上E存储时需要+127或+1023是为了解决浮点数,(-1,1)注意是不包含边界数的关系,的存储问题。
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1。
比如:
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其E为-1+127=126,表示为:
01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进 制表示形式为:
0 01111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于 0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
回答一开始提出的两个问题
1)为什么浮点数不能执行位运算;
答:整形执行位运算,准确的来说是无符号整形,才能执行位运算
移位运算:<<和>>
左移,一位相当于数字*2(加倍)
右移,相当于数字/2
根据浮点数的结构来看,浮点数,明显是达不到这样的效果的。
大家拿起笔,思考一下,浮点数执行,按位与&,按位或|,按位异或等运算时,是何种情况。
2)浮点型数据转换为整形数据时,编译器内部做了什么样的处理?
答:
#include <stdio.h>
#include <stdlib.h>
int main()
{ int a=1090;
float b=1020.23;
a=b;
printf("a的值为%d:",a);
return 0;
}
看输出结果:

看起来是似乎很合理?浮点数直接去掉小数部分,直接将自己的整数部分,赋值给了整形数据.其实编译器是先将浮点数值算出来,再截取整数部分截取给整形数据。
相关文章:

C语言中的浮点数存储
首先明确一个概念:C语言中整形是按照二进制存储在内存中,浮点型是按科学计数法存储在内存中(本质上存储的还是二进制数据0和1)。 如果没看懂这句话,没关系!看完以下正文,你就会豁然开朗&#x…...
Pypputeer自动化
Pyppeteer简介 pyppeteer 是 Python 语言的一个库,它是对 Puppeteer 的一个非官方端口,Puppeteer 是一个 Node 库,Puppeteer是Google基于Node.js开发的一个工具,它提供了一种高层次的 API 来通过 DevTools 协议控制 Chrome 或 Ch…...
selenium爬虫爬取当当网书籍信息 | 最新!
如果对selenium不了解的话可以到下面的链接中看基础内容: selenium爬取有道翻译-CSDN博客 废话不多说了下面是代码并且带有详细的注释: 爬取其他类型的书籍和下面基本上是类似的可以自行更改。 # 导入所需的库 from selenium import webdriver from …...

PTA 7-1 最大子列和问题
给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4,…...
JAVA实现向Word模板中插入Base64图片和数据信息
目录 需求一、准备模板文件二、引入Poi-tl、Apache POI依赖三、创建实体类(用于保存向Word中写入的数据)四、实现Service接口五、Controller层实现 需求 在服务端提前准备好Word模板文件,并在用户请求接口时服务端动态获取图片。数据等信息插…...
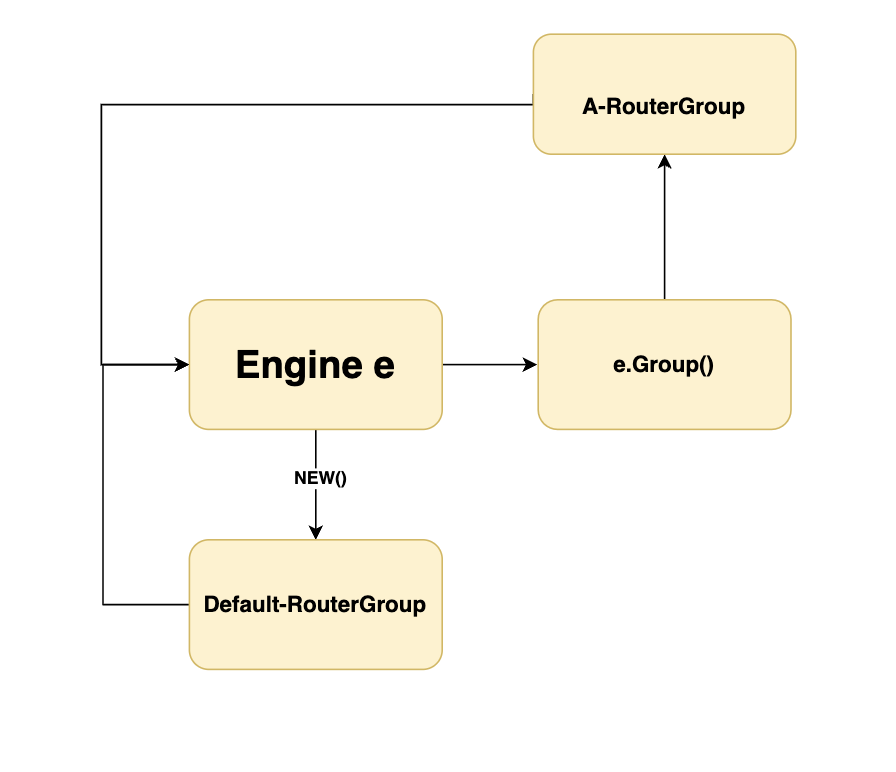
深入浅出关于go web的请求路由
文章目录 前言一、是否一定要用框架来使用路由?二、httprouter2.1 httprouter介绍2.2 httprouter原理2.3 路由冲突情况 三、gin中的路由四、hertz中的路由总结 前言 最近重新接触Go语言以及对应框架,想借此机会深入下对应部分。 并分享一下最近学的过程…...
HarmonyOS—开发环境诊断的功能
为了大家开发应用/服务的良好体验,DevEco Studio提供了开发环境诊断的功能,帮助大家识别开发环境是否完备。可以在欢迎界面单击Help > Diagnose Development Environment进行诊断。如果已经打开了工程开发界面,也可以在菜单栏单击Help >…...
Golang个人web框架开发-学习流程
Golang-个人web框架 github仓库创建github仓库 web框架学习开发周期第一阶段--了解第一阶段思考小结 第二阶段第三阶段 github仓库 github地址:ameamezhou/golang-web-frame 后续还将继续学习更新 创建github仓库 设置免密登录 ssh-keygen 一路回车就OK 上面有告…...
:Spring Bean如何保证并发安全)
java面试题(23):Spring Bean如何保证并发安全
1 问题分析 我们知道默认情况下,Spring中的Bean是单例的,所以在多线程并发访问的时候,有可能会出现线程安全问题。 2 解决方案 有几个方面的解决思路: 我们可以设置Bean的作用域设置为原型(prototype)&a…...
HarmonyOS【应用服务开发】在模块中添加Ability
Ability是应用/服务所具备的能力的抽象,一个Module可以包含一个或多个Ability。应用/服务先后提供了两种应用模型: FA(Feature Ability)模型: API 7开始支持的模型,已经不再主推。Stage模型:AP…...

根据屏幕尺寸设置html根字号fontSize大小并刷新
<script> // rem等比适配配置文件 // 基准大小 const baseSize 16 // 设置 rem 函数 function setRem() {// 当前页面宽度相对于 1920宽的缩放比例,可根据自己需要修改。const scale document.documentElement.clientWidth / 1920console.log(document.docu…...

Flutter 中的 InteractiveViewer:轻松实现交互性
在Flutter中,为了创建具有交互性的用户界面,我们通常需要使用各种手势检测和动画。然而,Flutter提供了一个强大而简便的小部件,即InteractiveViewer,它可以帮助我们轻松实现拖动、缩放和其他手势交互效果。本文将介绍I…...
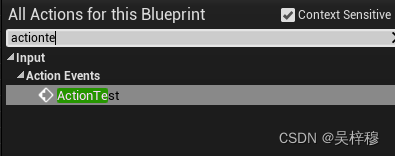
UE4 添加按键输入事件 并在蓝图中使用按键输入节点
绑定按键 选择Edit/ProjectSettings/Engine/Input 在bindings中可以选择添加ActionMappings或则AxisMappings ActionMappings:按键事件,有按下和抬起两个事件,需要分别用两个键触发AxisMappings:输入事件,返回值为float,对于键盘…...

Go 语言命名规范:清晰、简洁、一致
Go 语言命名规范:清晰、简洁、一致 Go 语言是一门注重简洁和一致性的编程语言,良好的命名规范是代码可读性和维护性的关键因素之一。在本篇博客中,我们将深入探讨 Go 语言的命名规范,包括标识符、包名、常量、变量、函数等各个方…...

代码随想录训练营第三十期|第十天|栈与队列part01|理论基础● 232.用栈实现队列● 225. 用队列实现栈
232. 用栈实现队列 - 力扣(LeetCode) class MyQueue {Stack<Integer> in;Stack<Integer> out;public MyQueue() {in new Stack<>();out new Stack<>();}public void push(int x) {in.push(x);}public int pop() {move();retu…...
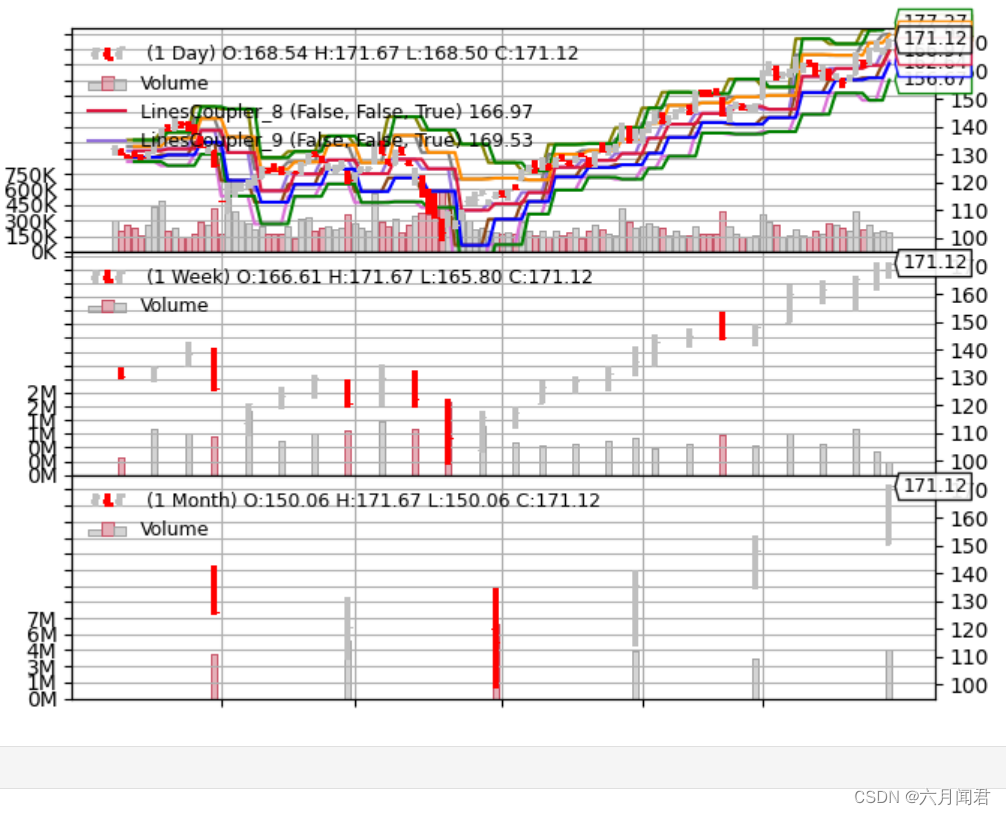
Backtrader 文档学习-Indicators混合时间框架
Backtrader 文档学习-Indicators混合时间周期 1.不同时间周期 如果数据源在Cerebro引擎中具有不同的时间范围和不同的长度,指示器将会终止。 比如:data0是日线,data1是月线 。 pivotpoint btind.PivotPoint(self.data1) sellsignal self…...

网络攻击与检测防御:维护数字安全的关键挑战
随着数字化时代的深入,网络攻击已成为企业和个人面临的严峻挑战之一。本文将深入探讨不同类型的网络攻击,以及有效的检测和防御策略,以确保网络系统的安全性和稳定性。 1. 常见网络攻击类型: DDoS 攻击:分布式拒绝服…...
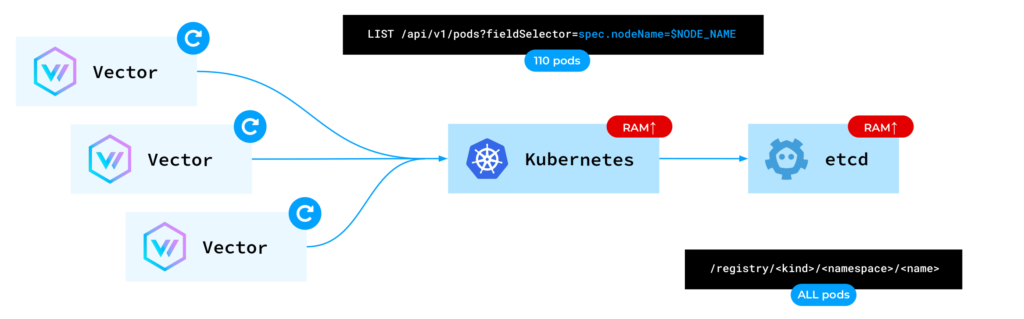
使用 Vector 在 Kubernetes 中收集日志
多年来,我们一直在使用 Vector 在我们的 Kubernetes 平台中收集日志,并成功地将其应用于生产中以满足各种客户的需求,并且非常享受这种体验。因此,我想与更大的社区分享它,以便更多的 K8s 运营商可以看到潜力并考虑他们…...
 篇)
ardupilot开发 --- 固件定制(OEM) 篇
0. 前言 固件功能定制OEM Customization: 原厂设备制造商OEM(Original Equipment Manufacturer)、代工功能勾选参数预设固件名称自定义 1. 基于某个飞控硬件来定制自己的飞控产品 可以自定义的包括:固件名称、预设参数、lua脚本…...

爬虫代理IP在电商行业的应用
随着互联网的快速发展,电商行业已经成为人们购物的主要渠道之一。在电商行业中,数据分析和挖掘至关重要。爬虫代理IP作为一种能够提供大量模拟请求和收集数据的工具,被广泛应用于电商行业。下面介绍爬虫代理IP在电商行业中的应用。 1、保护隐…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
