递归、搜索与回溯算法(专题一:递归)
往期文章(希望小伙伴们在看这篇文章之前,看一下往期文章)
(1)递归、搜索与回溯算法(专题零:解释回溯算法中涉及到的名词)【回溯算法入门必看】-CSDN博客
接下来我会用几道题,来让同学们利用我在专题零中提到的递归的宏观思想来解决这些题目。
目录
1. 汉诺塔
2. 合并两个有序链表
3. 反转链表
4. 两两交换链表中的结点
5. 快速幂
解法一 暴力循环
解法二 不断拆分
解法三 利用了二进制的特点
1. 汉诺塔
这道题可以说是递归最经典的题目之一,接下来我们就从这道题入手,重新认识一下递归是什么?
力扣题目链接

解析:
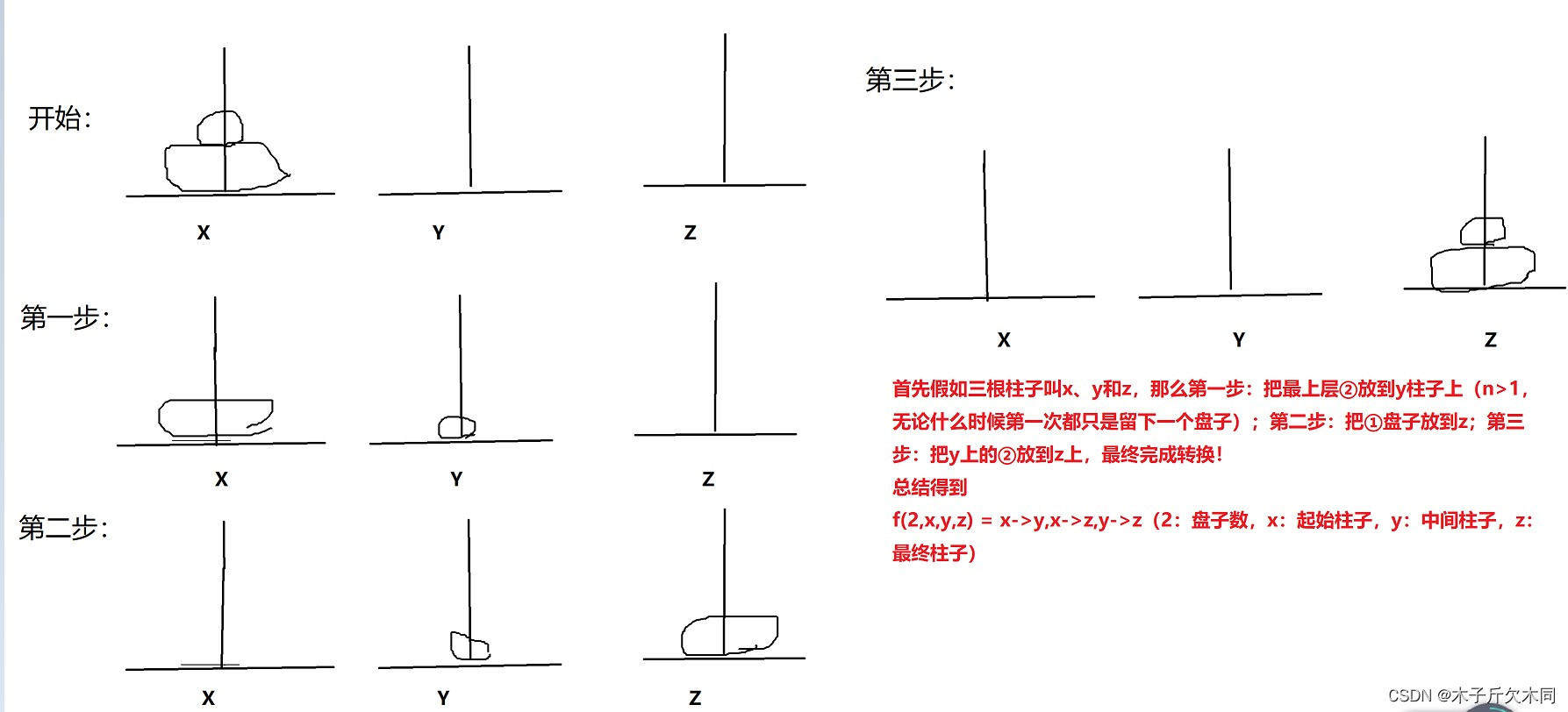
总结:我们想知道n个盘子的次数,记住了,在求解f(n)的时候,我们直接默认f(n - 1)已经完了就可以了!这个在前面已经解释过了,在此不再鳌述。我们将n-1个盘子当作一个整体:这就是类似于分治求解子问题的思想
那么当由3个盘子时,就有公式:f(3,x,y,z) = f(2,x,z,y),x->z,f(2,y,x,z);当有4个盘子时,就有公式:f(4,x,y,z) = f(3,x,z,y),x->z,f(3,y,x,z).从而推出f(n,x,y,z) = f(n,x,z,y),x->z,f(n,y,x,z)!
综上所述:也就是说我们想移动n个盘子,就需要先移动n - 1个盘子;移动n - 1个盘子,就需要先移动n - 2个盘子 ………………;移动2个盘子,就必须先移动1个盘子;
(1)而移动1个盘子就是递归的终止条件
(2)而n个盘子变成n - 1个盘子就是递归的大问题变成小问题的方法
宏观角度分析递归:
再来回顾,宏观的细节
- 一:不要在意递归的细节展开图
- 二:把递归的函数当成一个“黑盒”
- 三:我们的无条件的相信“黑盒”可以为我们解决当前的子问题(再次强调,递归中的每个子问题的解题步骤都是一样)
具体构建一个递归算法:
(1)创建函数头 ——> 从重复子问题入手,将x柱子上的盘子,借助y柱子转移到z柱子上。从而有函数头为:dfs(int x,int y,int z,int n); x、y和z代表了柱子,n代表现在多少个盘子需要移动。x是开始柱,y是中转柱,z是目的柱。
(2)确定函数体 ——> 无条件相信他能帮我们解决每一个子问题的。
重复的子问题如下:
- 如从 x 号柱子将n - 1个盘子借助 z 号柱子移动到 y 号柱子上
- 将 x 号柱子将最后一个盘子移动到 z 号柱子上
- 将 y 号柱子上的n - 1个盘子移动到 z 号柱子上
从而有函数体为:
① dfs(x,z,y,n - 1); ② x.back -> z; ③ dfs(y,x,z,n - 1);
(3)递归出口:当剩下一个盘子的时候,也就是n == 1时。x.back -> z即可。
//宏观角度分析递归//1.创建函数头//2.确定函数体,无条件相信他能帮我们解决每一个子问题的//3.递归出口public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {dfs(A,B,C,A.size());}public void dfs(List<Integer> x,List<Integer> y,List<Integer> z,int size){//递归出口if(size == 1){z.add(x.remove(x.size() - 1));return;}//封装一个小黑盒//将x柱上的size - 1个盘子通过z柱子移动到y柱子上dfs(x,z,y,size - 1);//将a柱上的最后一个盘子移动到c柱子上z.add(x.remove(x.size() - 1));//将b柱上的size - 1个盘子通过a柱子移动到c柱子上dfs(y,x,z,size - 1);}
2. 合并两个有序链表
力扣题目链接
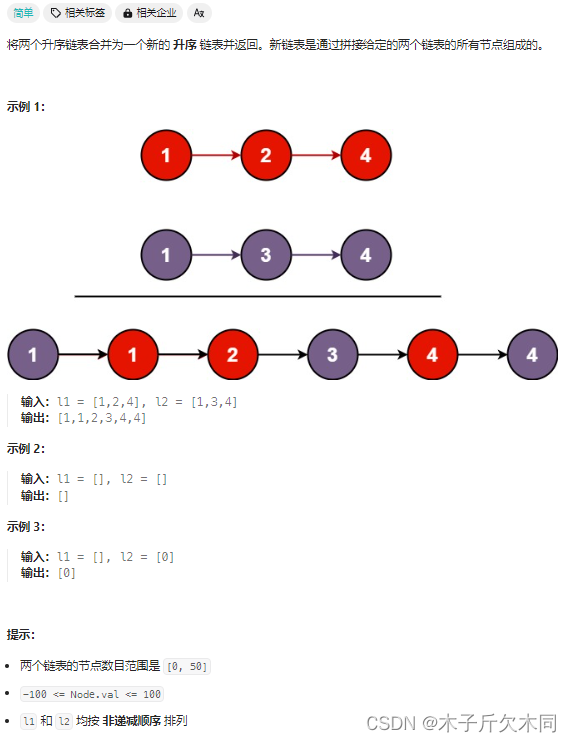
解析:
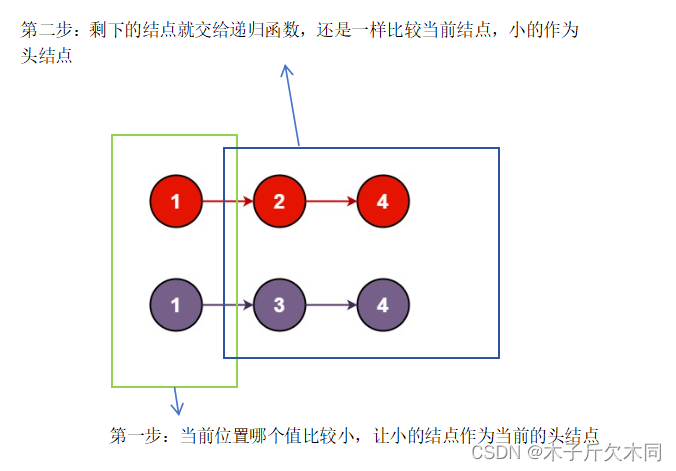
(1)递归函数的含义:交给你两个链表的头结点,你帮我把它们合并起来,并且返回合并后的头结点。
(2)函数体:选择两个头结点中较⼩的结点作为最终合并后的头结点,然后将剩下的链表交给递归函数去处理。
(3)递归出⼝:当某⼀个链表为空的时候,返回另外⼀个链表。
// 法一:递归法public ListNode mergeTwoLists(ListNode l1, ListNode l2) {// 递归出口:当l1或者l2为空,就返回另一个不为空的链表if (l1 == null)return l2;if (l2 == null)return l1;//如果l1的值小于l2,那么就让l1作为头结点,剩下的结点继续比较if (l1.val <= l2.val) {l1.next = mergeTwoLists(l1.next,l2);return l1;}else{l2.next = mergeTwoLists(l1,l2.next);return l2;}}
3. 反转链表
力扣题目链接
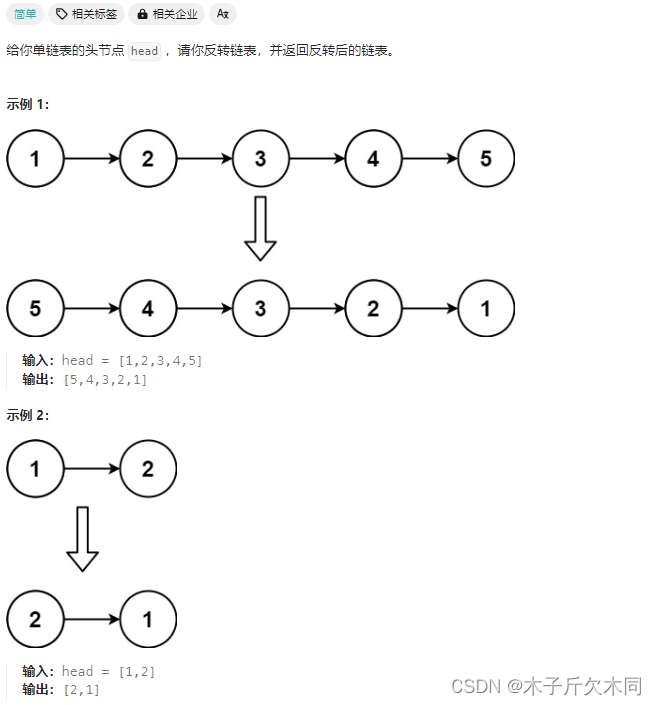

解析:
(1)递归函数的含义:交给你⼀个链表的头指针,你帮我逆序之后,返回逆序后的头结点。
(2)函数体:先把当前结点之后的链表逆序,逆序完之后,把当前结点添加到逆序后的链表后⾯即可。(相同的子问题)
(3)递归出⼝:当前结点为空或者当前只有⼀个结点的时候,不⽤逆序,直接返回。
public ListNode reverseList(ListNode head) {return dfs(head);}public ListNode dfs(ListNode h){//递归出口:直接到找最后一个结点,类似后序遍历if(h == null || h.next == null){return h;}//找最后一个结点ListNode newNode = dfs(h.next);//从倒数第二个结点开始h.next.next = h;h.next = null;return newNode;}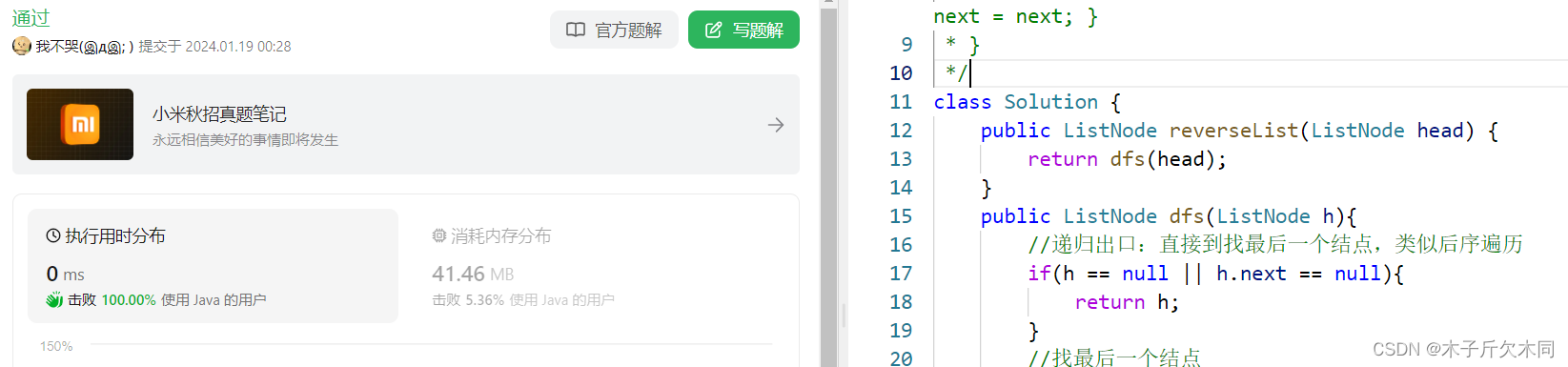
4. 两两交换链表中的结点
力扣题目链接
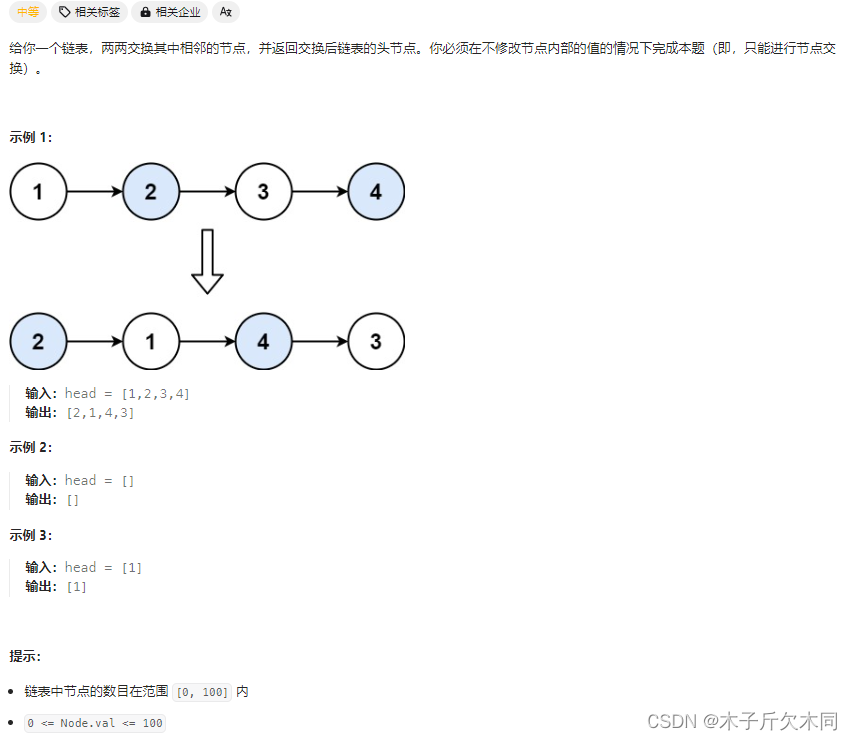
解析:
(1)递归函数的含义:交给你⼀个链表,将这个链表两两交换⼀下,然后返回交换后的头结点。
(2)函数体:先去处理⼀下第⼆个结点往后的链表,然后再把当前的两个结点交换⼀下,连接上后⾯处理后的链表。(相同的子问题)
(3)递归出⼝:当前结点为空或者当前只有⼀个结点的时候,不⽤交换,直接返回。
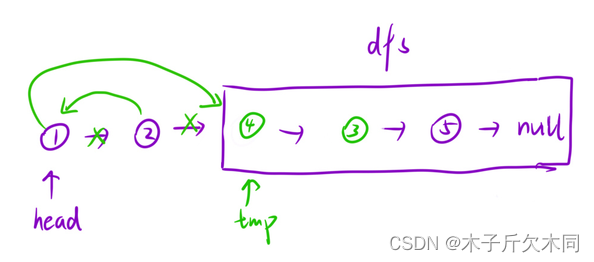
//后序遍历public ListNode swapPairs(ListNode head) {//链表中节点的数目在范围 [0, 100] 内//如果只剩下一个结点就没必要交换了,因为是两两交换if(head == null || head.next == null){return head;}//先去交换在我之后之后的结点ListNode newNode = swapPairs(head.next.next);ListNode ret = head.next;head.next = newNode;ret.next = head;return ret;}要先修改后面结点,再能修改当前结点,很类似后序遍历的方式。
5. 快速幂
力扣题目链接

解法一 暴力循环
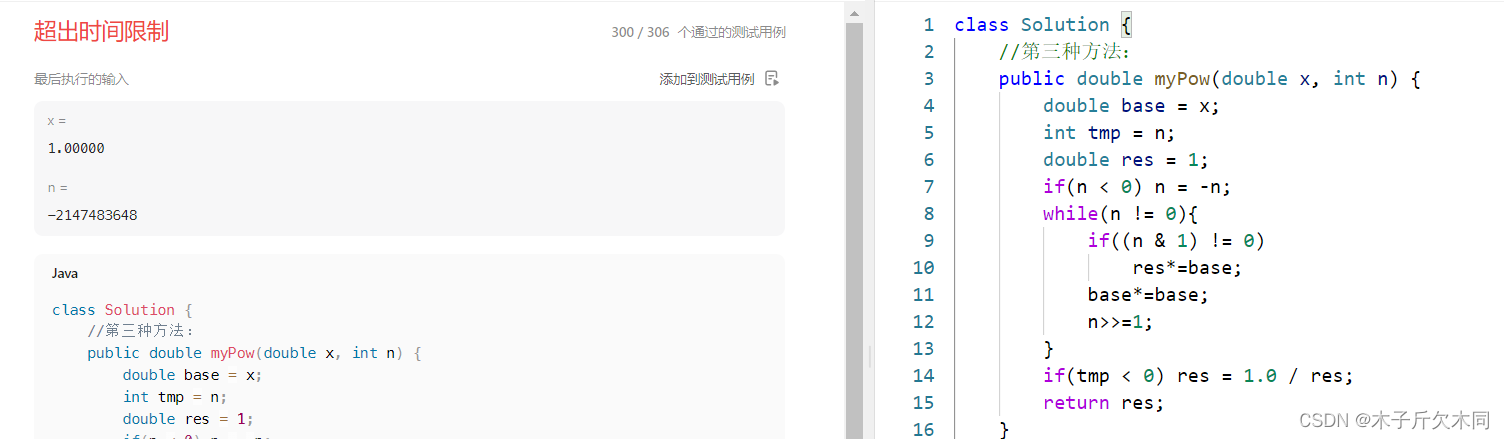
public double myPow(double x, int n) {double ret = 1;int tmp = n;if(n < 0) n = -n;for(int i = 1;i <= n;i++){ret *= x;}if(tmp < 0) ret = 1.0 / ret;return ret;}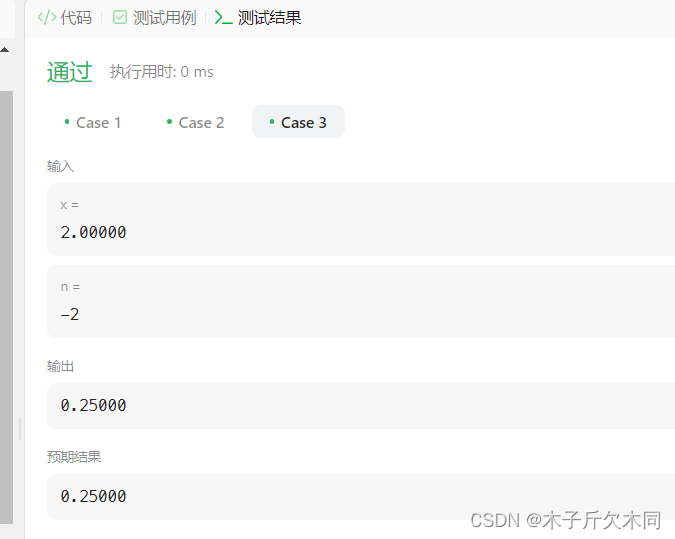
暴力循环可以解决较小的幂,当幂的值比较大就会报超时的错误!!!

所以有了如下两个改进方案:
解法二 不断拆分
(1)递归函数的含义:求出 x 的 n 次⽅是多少,然后返回。
(2)函数体:先求出 x 的 n / 2 次⽅是多少,然后根据 n 的奇偶,得出 x 的 n 次⽅是多少。
(3)递归出⼝:当 n 为 0 的时候,返回 1 即可 。

//第二种方法:public double myPow(double x, int n) {return n < 0 ? 1.0 / pow(x,-n) : pow(x,n);}public double pow(double x,int n){if(n == 0)return 1.0;double tmp = pow(x,n/2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}
解法三 利用了二进制的特点
例如算:
分解:
(1)而、
、
是倍乘关系,所以算
不用11个a相乘,而是
得到,
,而
得到。
(2)那么问题来了,如何将11分解成 11 = 8 + 2 + 1这样的倍乘关系呢?
答:
(3)这里因为二进制的11中第三位为0,所以没有 ,如果跳过4呢?1011中的0,就是需要跳过的 4。
(4)
推算乘积:从低位往高位处理1011(右移一次,就把刚处理的低位移走了)
- 1011,处理末尾的1:计算a。
;
- 1011,处理第2个1:计算
。
;
- 1011,处理0:跳过
。
- 1011,处理1:计算
。
。
//第三种方法:public double myPow(double x, int n) {double base = x;int tmp = n;double res = 1;if(n < 0) n = -n;while(n != 0){if((n & 1) != 0) //如果n的最后一位是1,表示这个地方需要乘res*=base;base*=base;//推算乘积,在解析有说明n>>=1;//n右移一位,把刚处理过n的最后一位去掉}if(tmp < 0) res = 1.0 / res;return res;}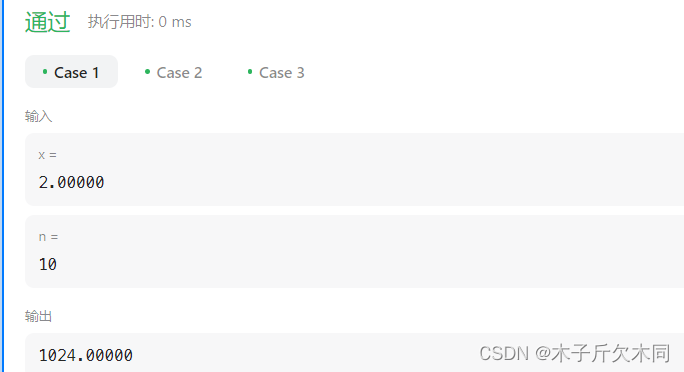
注:解法三的速度比解法一快了许多,但是相比于解法二还是慢了一些,导致超时错误。
相关文章:

递归、搜索与回溯算法(专题一:递归)
往期文章(希望小伙伴们在看这篇文章之前,看一下往期文章) (1)递归、搜索与回溯算法(专题零:解释回溯算法中涉及到的名词)【回溯算法入门必看】-CSDN博客 接下来我会用几道题&#…...

element-ui 打包流程源码解析(下)
目录 目录结构和使用1,npm 安装1.1,完整引入1.2,按需引入 2,CDN3,国际化 接上文:element-ui 打包流程源码解析(上) 文章中提到的【上文】都指它 ↑ 目录结构和使用 我们从使用方式来…...

ChatGPT给出的前端面试考点(Vue.js)
ChatGPT给出的前端面试考点(Vue.js) 答案 1. Vue.js是什么?它的主要特点是什么? Vue.js是一个渐进式JavaScript框架,用于构建用户界面。它的主要特点包括: 数据绑定:Vue.js使用双向数据绑定&…...

ChatGPT 商业提示词攻略书
原文:ChatGPT Business Prompt Playbook 译者:飞龙 协议:CC BY-NC-SA 4.0 一、书系介绍 人工智能发展迅速。非常迅速。 所以我希望你做两件事: (1) 在 Twitter 上关注我:iamkylebalmer (2) 订阅我的免费电子邮件通…...
Notepad++运行C语言输出乱码
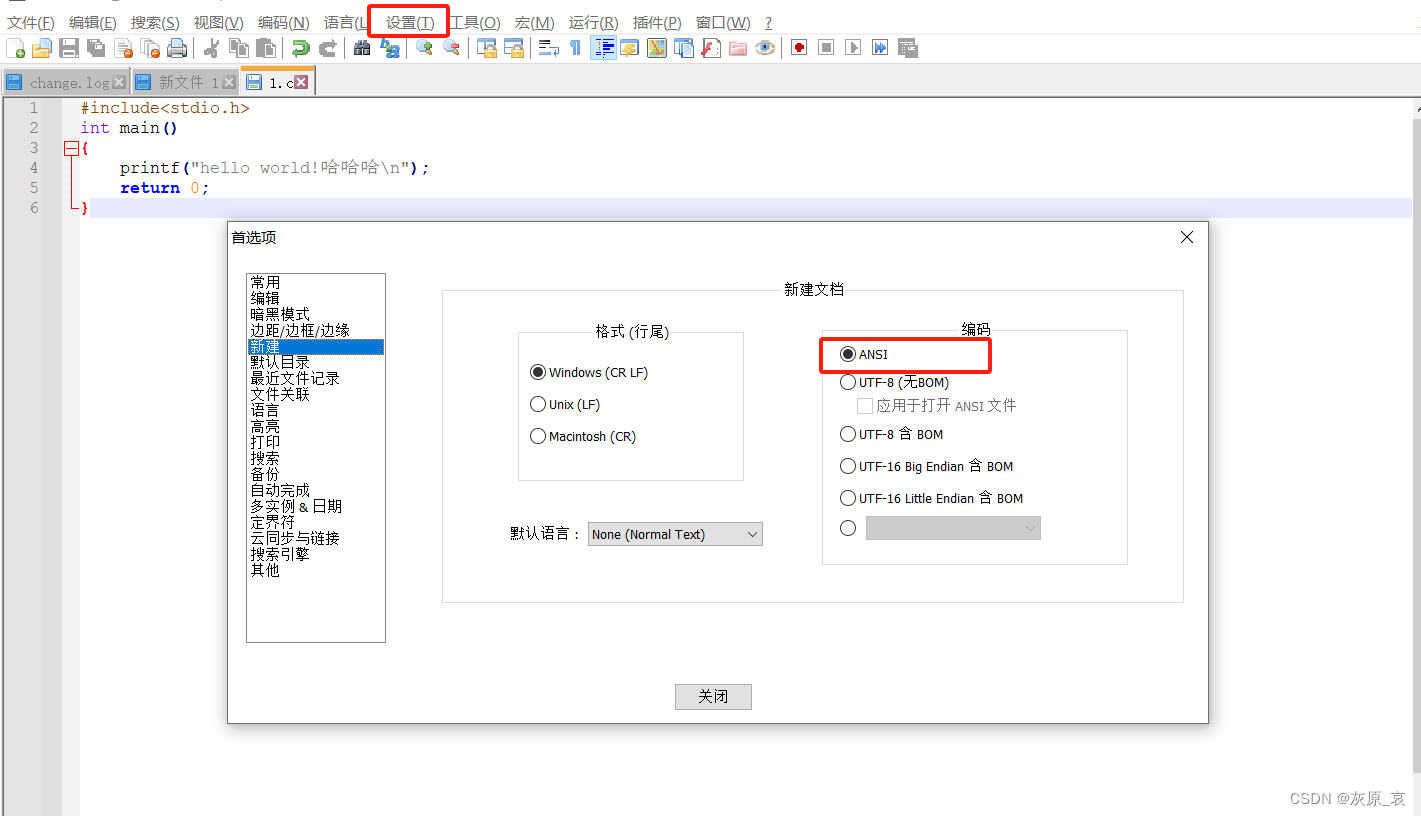
方法一:编码-编码字符集-中文-GB2312 这时原程序中文会变成乱码,我是重新输入中文 重新编译执行即可 缺陷:重开一个程序有中文还是会显示乱码,需要重新设置编码,比较麻烦 方法二:设置-首选项-新建-右侧编…...
深入解析 Java 方法引用:Lambda 表达式的进化之路
前言 方法引用是 Java 8 提供的一种新特性,它允许我们更简洁地传递现有方法作为参数。这项特性实际上是对 Lambda 表达式的一种补充,通过方法引用,我们可以直接引用现有方法,而无需编写完整的Lambda表达式。最近在使用方法引用的…...
多表查询)
MySQL作业 (3)多表查询
多表查询 1.创建student和score表2.为student表和score表增加记录3.查询student表的所有记录4.查询student表的第2条到4条记录5.从student表查询所有学生的学号(id)、姓名(name)和院系(department)的信息6.…...

ConcurrentHashMap和HashMap的区别
什么是HashMap (1)HashMap 是基于 Map 接口的非同步实现,线程不安全,是为了快速存取而设计的;它采用 key-value 键值对的形式存放元素(并封装成 Node 对象),允许使用 null 键和 nul…...

MCM备赛笔记——图论模型
Key Concept 图论是数学的一个分支,专注于研究图的性质和图之间的关系。在图论中,图是由顶点(或节点)以及连接这些顶点的边(或弧)组成的。图论的模型广泛应用于计算机科学、通信网络、社会网络、生物信息学…...

算法笔记(动态规划入门题)
1.找零钱 int coinChange(int* coins, int coinsSize, int amount) {int dp[amount 1];memset(dp,-1,sizeof(dp));dp[0] 0;for (int i 1; i < amount; i)for (int j 0; j < coinsSize; j)if (coins[j] < i && dp[i - coins[j]] ! -1)if (dp[i] -1 || dp[…...

开发实践_阶段三
编写一个告知APP。 需求: 1.登录、注册 2.发布定向讯息:检测是否登录,是则向用户或用户组发布 ”名称 时间“ ;否则提示登录 3.讯息接收:检测是否登录,是则查看收到信息(未读数)…...

codegeex和通义灵码辅助编程——以及通义灵码无法登陆的bug解决
通义的速度更快,延迟低,150ms。 codegeex速度慢些,延迟较高,500ms。 个人评价:延迟低的会很好地改善使用体验,所以通义加分。 但是整体功能上还是codegeex强一些,可以选中代码进行对话…...

Android14之DefaultKeyedVector实现(一百八十二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
银河麒麟操作系统 v10 中离线安装 Docker
银河麒麟操作系统 v10 中离线安装 Docker 1. 查看系统版本2. 查看 Linux 内核版本(3.10以上)3. 查看 iptabls 版本(1.4以上)4. 判断处理器架构5. 离线下载 Docker 安装包6. 移动解压出来的二进制文件到 /usr/bin 目录中7. 配置 Do…...

如何系统的学习Python
学习 Python 的时候,可以按照以下步骤进行系统学习: 学习 Python 基础知识:首先了解 Python 的基础语法、数据类型、变量和运算符等基本概念。可以通过阅读《Python编程从入门到实践》等经典教材来建立基础。也可以通过翻阅Python官方文档来进…...

Java并发基础:一文讲清util.concurrent包的作用
java.util.concurrent包是 Java 中用于并发编程的重要工具集,提供了线程池、原子变量、并发集合、同步工具类、阻塞队列等一系列高级并发工具类,使用这些工具类可以极大地简化并发编程的难度,减少出错的可能性,提高程序的效率和可…...

C++PythonC# 三语言OpenCV从零开发(2):教程选择
文章目录 相关专栏前言视频教学和官方文档视频教程OpenCV 官方教程最终选择我的最终选择 相关专栏 C&Python&Csharp in OpenCV 前言 OpenCV 有官方的教程和简单的视频教程: OpenCV 官方教程 B站也有相关的视频教学 OpenCV4 C 快速入门视频30讲 - 系列合集 …...

【嘉立创EDA-PCB设计指南】3.网络表概念解读+板框绘制
前言:本文对网络表概念解读板框绘制(确定PCB板子轮廓) 网络表概念解读 在本专栏的上一篇文章【嘉立创EDA-PCB设计指南】2,将设计的原理图转为了PCB,在PCB界面下出现了所有的封装,以及所有的飞线属性&…...
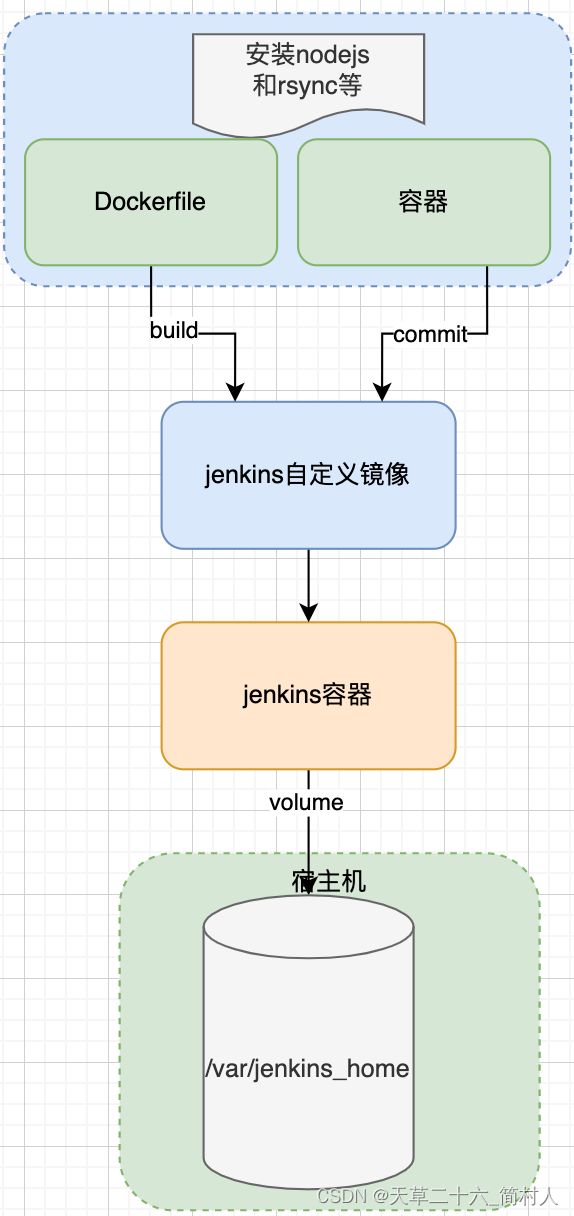
nodejs前端项目的CI/CD实现(二)jenkins的容器化部署
一、背景 docker安装jenkins,可能你会反问,这太简单了,有什么好讲的。 我最近就接手了一个打包项目,它是一个nodejs的前端项目,jenkins已在容器里部署且运行OK。 但是,前端组很追求新技术,不…...

python爬虫案例分享
当然,我可以分享一个基本的Python爬虫示例。这个示例将使用Python的requests库来抓取网页内容,然后使用BeautifulSoup库来解析和提取信息。我们将构建一个简单的爬虫来从一个示例网站抓取标题。 Python爬虫示例 目标 提取某网站的标题。 需要的库 r…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
