领略指针之妙
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk
⸝⋆ ━━━┓
- 个性标签 - :来于“云”的“羽球人”。 Talk is cheap. Show me the code
┗━━━━━━━ ➴ ⷯ本人座右铭 : 欲达高峰,必忍其痛;欲戴王冠,必承其重。
👑💎💎👑💎💎👑
💎💎💎自💎💎💎
💎💎💎信💎💎💎
👑💎💎 💎💎👑 希望在看完我的此篇博客后可以对你有帮助哟👑👑💎💎💎👑👑 此外,希望各位大佬们在看完后,可以互赞互关一下,看到必回
👑👑👑💎👑👑👑
想必各位老铁们也知道,C语言的灵魂就在于指针,他很神奇,就像一把神奇的钥匙,可以打开指定的房间。有了这个精确的地址,我们也就不用再怕迷路了,哈哈哈。
OK,话不多说,接下来给各位老铁们看个神奇的代码,没错,就是此时屏幕前的你,顺便看看自己是否对指针轻松拿捏,不过话说在前面,下面这个代码要是对指针没有一定的功力再结合“码图”(也就是画图),可不是件容易的事
题目:
#include<stdio.h>
int main()
{char* c[] = { "ENTER","NEW","POINT","FIRST" };char** cp[] = { c + 3,c + 2,c + 1,c };char*** cpp = cp;printf("%s\n",**++cpp );printf("%s\n", *--* ++cpp +3);printf("%s\n", *cpp[-2]+3);printf("%s\n",cpp[-1][-1]+1 );return 0;
}
各位老铁们咱也就动起来吧,看看自己咋样
分析:
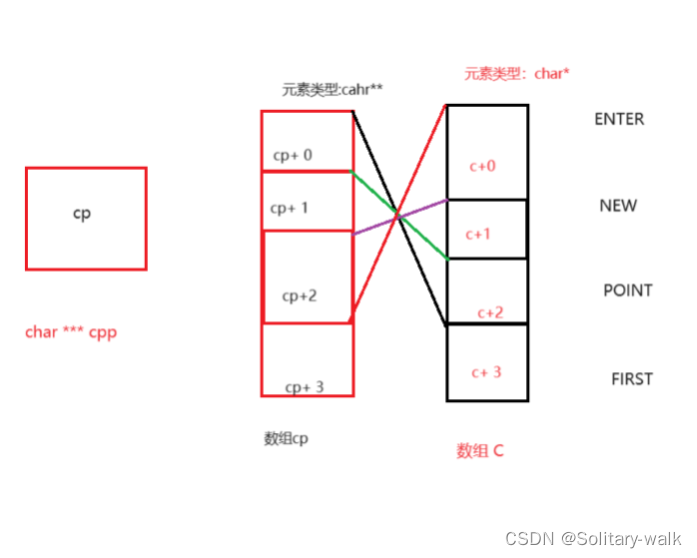
1)初始状态对应的草图
2)**++cpp的分析
1:cpp初始状态是指向数组cp的首元素的地址
2:++cpp注意这是前置加加(也就意味着cpp的指向要改变,同时也会对后面cpp的一系列操作有影响)cpp此时指向cp数组的第二个元素的地址
3:**++cpp 第一次解引用是指向c+2,再一次解引用是指向POINT这个字符串所指向的首元素地址
4:结果:POINT
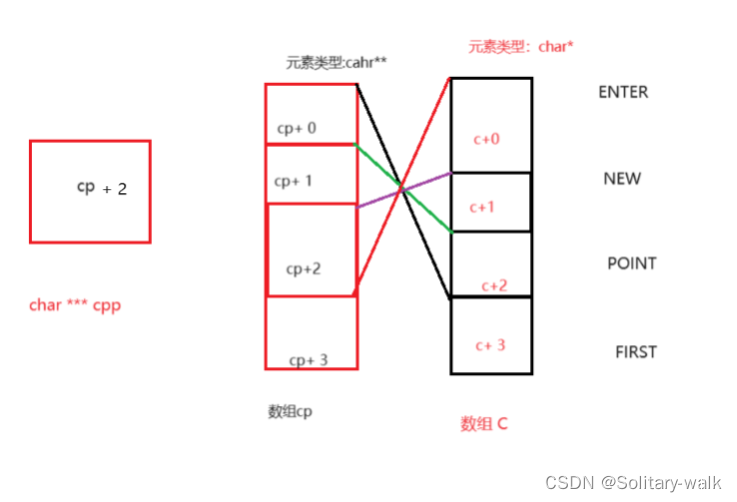
3)*--* ++cpp +3
草图如下:
1:看到这个表达式可能有些老铁会发懵,不知从何下手(优先级)
2:++cpp:指向数组cp的第二个元素(cp+2)
3:此时对++cpp进行解引用:指向数组C第二个元素的地址(c+1),再--指向的是数组C第一个元素的地址(c+ 0)对他进行解引用指向ENTER这个字符串首字符地址
4:此时最后指向 +3 的操作:对字符串跳过三个字符指向 E
5:打印结果: ER
4)*cpp[-2]+3
1:*cpp[-2]+3 == *(*(cpp - 2)) +3
2:cpp指向数组cp的第二个元素(cp+2)
3:cpp -2指向 cp+0
4:*(cpp-2)访问的是 c+3
5:*(*(cpp-2)) 访问的是字符串 FIREST指向的第一个字符从地址
6: *(*(cpp - 2)) +3 此时指向 E的地址
7:打印:ST
5) cpp[-1][-1]+1
1:cpp[-1][-1]+1 == *(*(cpp-1)-1) +1
2:cpp-1 == cp+2-1 是指向 cp+1
3:此时解引用是指向 c+2 的地址 ,此时在对这个地址-1,是指向c+1这个地址
4:*(*(cpp-1)-1)此时是的 c+1这个地址进行解引用(指向NEW的首字符地址)
注意:可不是对c+ 2 这个地址解引用(错在:对cpp-1后忘了解引用,就比如说我,嘻嘻嘻)
5: *(*(cpp-1)-1) +1 指向 E这个字符对应的地址
6:打印 :EW
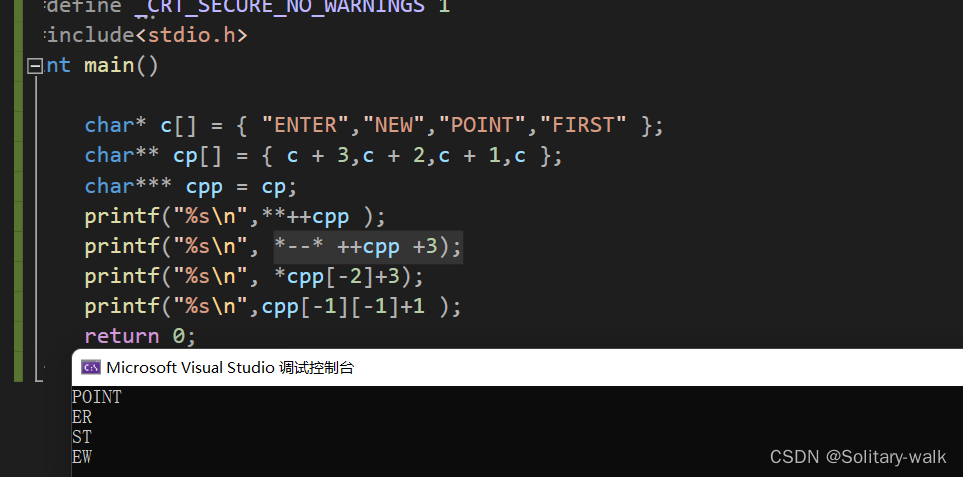
分析半天是对是错呢,咱让程序跑起来也看一眼:
结果:
结语:
或许这就是编程的魅力,我永远沉迷于此,陶醉其中。希望各位老铁看到我的这篇博客可以对指针有更深的理解,也希望"小白"也能有所收获,不过咱还是有啥说啥,这确实是需要一点点的功力的,没有点底子可能或许稍微吃力,欧克,又到了各位主角的舞台了(咱一波关注,一波赞走起,也是更好激励我的)
温馨提示:最近天气比较极端,希望各位老铁照顾好自己,生病真的很难受,状态也不在线(我就是扛了一周左右)
相关文章:
领略指针之妙
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk ⸝⋆ ━━━┓ - 个性标签 - :来于“云”的“羽球人”。…...
迭代器模式介绍
目录 一、迭代器模式介绍 1.1 迭代器模式定义 1.2 迭代器模式原理 1.2.1 迭代器模式类图 1.2.2 模式角色说明 1.2.3 示例代码 二、迭代模式的应用 2.1 需求说明 2.2 需求实现 2.2.1 抽象迭代类 2.2.2 抽象集合类 2.2.3 主题类 2.2.4 具体迭代类 2.2.5 具体集合类 …...

算法每日一题: 最大字符串匹配数目 | 哈希 | 哈希表 | 题意分析
hello 大家好,我是星恒 今天给大家带来的是hash,思路有好几种,需要注意的是这中简单的题目需要仔细看条件,往往他们有对应题目的特殊的解法 题目:leetcode 2744给你一个下标从 0 开始的数组 words ,数组中包…...

自然语言处理(Natural Language Processing,NLP)解密
专栏集锦,大佬们可以收藏以备不时之需: Spring Cloud 专栏:http://t.csdnimg.cn/WDmJ9 Python 专栏:http://t.csdnimg.cn/hMwPR Redis 专栏:http://t.csdnimg.cn/Qq0Xc TensorFlow 专栏:http://t.csdni…...

【DevOps-08-5】目标服务器准备脚本,并基于Harbor的最终部署
一、简要描述 告知目标服务器拉取哪个镜像判断当前服务器是否正在运行容器,停止并删除如果目标服务器已经存在当前镜像,删除当前版本的镜像目标服务器拉取Harbor上的镜像将拉取下来的镜像运行成容器二、准备目标服务器脚本文件 1、在部署的目标服务器准备deploy.sh部署脚本 …...

用Java实现01背包问题 用贪心算法
贪心算法不是解决01背包问题的有效方法,因为贪心算法只能保证得到一个近似最优解,而无法保证得到最优解。因此,我们需要使用动态规划来解决01背包问题。以下是使用Java实现的动态规划解法: public class KnapsackProblem {public…...

JUC并发编程-8锁现象
5. 8锁现象 如何判断锁的是谁!锁到底锁的是谁? 锁会锁住:对象、Class 深刻理解我们的锁 问题1 两个同步方法,先执行发短信还是打电话 public class dome01 {public static void main(String[] args) {Phone phone new Phon…...
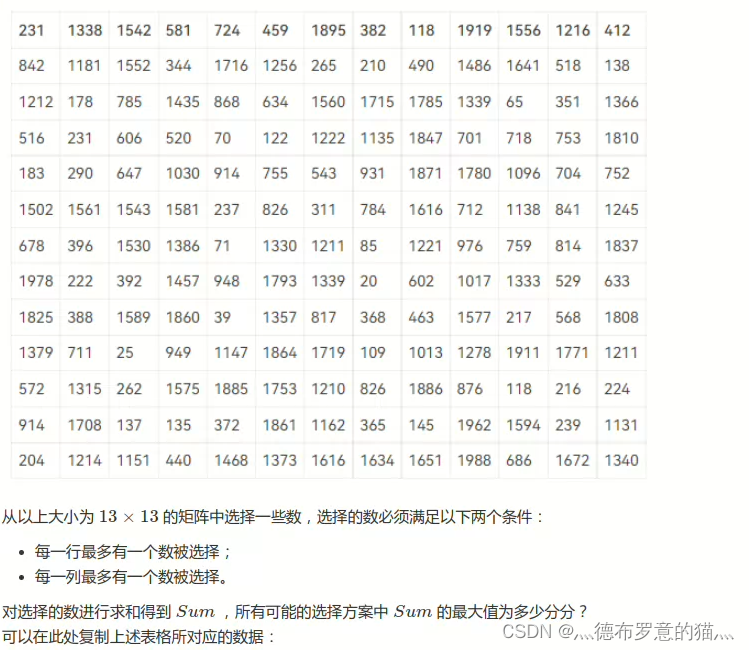
集美大学“第15届蓝桥杯大赛(软件类)“校内选拔赛 D矩阵选数
经典的状态压缩DP int dp[15][(1<<14)10]; int a[15][15]; void solve() {//dp[i][st]考虑到了第i行 并且当前考虑完第i行以后的选择状态是st的所有方案中的最大值for(int i1;i<13;i)for(int j1;j<13;j)cin>>a[i][j];for(int i1;i<13;i){for(int j0;j<…...

Android System Service系统服务--1
因为工作中经常需要解决一些framework层的问题,而framework层功能一般都是system service 的代理stub,然后封装相关接口,并提供给APP层使用,system service则在不同的进程中运行,这样实现了分层,隔离&#…...

【RT-DETR有效改进】华为 | Ghostnetv1一种专为移动端设计的特征提取网络
前言 大家好,这里是RT-DETR有效涨点专栏。 本专栏的内容为根据ultralytics版本的RT-DETR进行改进,内容持续更新,每周更新文章数量3-10篇。 专栏以ResNet18、ResNet50为基础修改版本,同时修改内容也支持ResNet32、ResNet101和PP…...

45个经典Linux面试题!赶紧收藏!
问题一: 绝对路径用什么符号表示?当前目录、上层目录用什么表示?主目录用什么表示? 切换目录用什么命令? 答案:绝对路径:如/etc/init.d当前目录和上层目录:./ …/主目录:~/切换目…...

将字符串中可能被视为正则表达式的特殊字符进行转义re.escape()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 将字符串中可能被视为 正则表达式的特殊字符 进行转义 re.escape() [太阳]选择题 请问以下代码最后输出的结果是? import re s [a-z] print("【显示】s ",s) print(&q…...

C语言:函数指针的使用
在C语言中,函数指针是指向函数的指针变量。它可以存储函数的地址,使得可以通过该指针来调用函数。以下是函数指针的基本概念和用法: 一、基本概念: 声明函数指针: returnType (*pointerName)(parameterTypes); 这里 r…...
)
「实战应用」如何用DHTMLX Gantt构建类似JIRA式的项目路线图(二)
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。 在web项目中使用DHTMLX Gantt时,开发人员经常需要满足与UI外观相关的各种需求。因此他们必须确定JavaScript甘特图库的…...

Webpack5入门到原理18:Plugin 原理
Plugin 的作用 通过插件我们可以扩展 webpack,加入自定义的构建行为,使 webpack 可以执行更广泛的任务,拥有更强的构建能力。 Plugin 工作原理 webpack 就像一条生产线,要经过一系列处理流程后才能将源文件转换成输出结果。 这条…...

PWM之舵机
舵机又称直流电机,如下图 本节承接上节,具体的PWM技术已经在上一节讲的很详细了,本节就不再讲了,那么我们的重点就放在直流电机的工作原理上了。 一、工作原理 我们研究直流电机,主要式研究直流电机旋转速度的调节&a…...
)
Python并发与多线程:IO并发(阻塞IO、非阻塞IO、IO多路复用、异步IO)
在Python中,有多种处理并发的方式,其中之一就是使用多线程进行IO并发操作。在IO操作中,有四种常见的方式:阻塞IO、非阻塞IO、IO多路复用和异步IO。 阻塞IO(Blocking IO):当执行一个IO操作时&…...

React16源码: React中的IndeterminateComponent的源码实现
IndeterminateComponent 1 )概述 这是一个比较特殊的component的类型, 就是还没有被指定类型的component在一个fibrer被创建的时候,它的tag可能会是 IndeterminateComponent在 packages/react-reconciler/src/ReactFiber.js 中,有…...

SpringBoot:详解Bean生命周期和作用域
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java项目分享》 《RabbitMQ》《Spring》《SpringMVC》 🛸学无止境,不骄不躁,知行合一 文章目录 前言一、生命周期二…...

【图解数据结构】顺序表实战指南:手把手教你详细实现(超详细解析)
🌈个人主页:聆风吟 🔥系列专栏:图解数据结构、算法模板 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. ⛳️线性表1.1 🔔线性表的定义1.2 🔔线性表的存储结构 二. ⛳️顺序表…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...