牛客周赛 Round 10 解题报告 | 珂学家 | 三分模板 + 计数DFS + 回文中心扩展
前言

整体评价
T2真是一个折磨人的小妖精,写了两版DFS,第二版计数DFS才过。T3是三分模板,感觉也可以求导数。T4的数据规模才n=1000,因此中心扩展的 O ( n 2 ) O(n^2) O(n2)当仁不让。
A. 游游的最长稳定子数组
滑窗经典题
从某个左端点出发,按顺序找到最远的右端点
然后把该右端点变成新的左端点,继续寻找直至结束
import java.io.*;
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));int n = sc.nextInt();int[] arr = new int[n];for (int i = 0; i < n; i++) arr[i] = sc.nextInt();int ans = 0;int j = 0;while (j < n) {int k = j + 1;while (k < n && Math.abs(arr[k] - arr[k - 1]) <= 1) {k++;}ans = Math.max(ans, k - j);j = k;}System.out.println(ans);}}
#include <bits/stdc++.h>using namespace std;int main() {int n;cin >> n;vector<int> arr(n);for (int i = 0; i< n; i++) {cin >> arr[i];}int res = 1;int j = 0;while (j < n) {int k = j + 1;while (k < n && abs(arr[k - 1] - arr[k]) <= 1) {k++;}res = max(res, k - j);j = k;}cout << res << endl;return 0;
}
B. 游游的字符重排
暴力搜索好像TLE了,而且需要额外处理去重
那如何搜索,可以不考虑去重的情况呢?
可以对每个字母进行频数统计
然后进行dfs,这样有一个好处,就是天然去重,时间复杂度为 O ( n ! ) O(n!) O(n!)
import java.io.*;
import java.util.*;public class Main {// 计数DFSpublic static int dfs(int[] nums, int n, int now, int prev) {if (now == n) {return 1;}int res = 0;for (int i = 0; i < nums.length; i++) {if (nums[i] > 0 && i != prev) {nums[i]--;res += dfs(nums, n, now + 1, i);nums[i]++;}}return res;}public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));char[] str = sc.next().toCharArray();Map<Character, Integer> hash = new HashMap<>();for (char c: str) hash.merge(c, 1, Integer::sum);int[] nums = hash.values().stream().mapToInt(x -> x).toArray();System.out.println(dfs(nums, str.length, 0, -1));}}#include <bits/stdc++.h>using namespace std;using int64 = long long;int64 dfs(const string &s, char last, int mask) {int n = s.length();if (mask == (1 << n) - 1) {return 1LL;}int64 res = 0;for (int i = 0; i < n; i++) {if ((mask & (1 << i)) == 0) {if (s[i] == last || (i > 0 && s[i] == s[i - 1] && (mask &(1 << (i - 1))) == 0) ) {continue;}res += dfs(s, s[i], mask | (1 << i));}}return res;
}int main() {string s;cin >> s;sort(s.begin(), s.end());int64 res = dfs(s, ' ', 0);cout << res << endl;return 0;
}
C. 游游开车出游
三分板子题,该函数为凹函数。
z = y / (v + x*t) + t
该函数先单调递减,然后单调递增
1. 三分板子
import java.io.BufferedInputStream;
import java.util.Scanner;public class Main {static double calc(double y, double x, double v, double t) {return y / (v + x * t) + t;}public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));double v = sc.nextDouble(), x = sc.nextDouble(), y = sc.nextDouble();// 三分板子double l = 0.0, r = 1e9;while (r - l >= 1e-7) {// 要求1e-6double s = (r - l) / 3.0;double t1 = l + s;double t2 = l + 2 * s;double res1 = calc(y, x, v, t1);double res2 = calc(y, x, v, t2);if (res1 >= res2) {l = t1;} else {r = t2;}}System.out.println(calc(y, x, v, l));}}
2. 求导
f(t) = y / (v + x*t) + t
求导
f‘(t) = -xy / (v + x*t)^2 + 1
求f’(t) = 0 的解
x^2 * t^2 + 2vx*t + v^2 - xy = 0; t为变量, x,y,v都是常数
t’=(-v +/- sqrt(xy)) / x,
不知道,牛客啥时候对latex语法不那么友好了,写起来难受,看的人更难受
因为xy>0, 所以一定有解,同时 t>=0, 因此只有一个可能解
t’ = (-v + sqrt(xy)) / x
t’ = max(0, t’), 保证t>=0
import java.io.BufferedInputStream;
import java.util.Scanner;public class Main {static double calc(double y, double x, double v, double t) {return y / (v + x * t) + t;}public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));double v = sc.nextDouble(), x = sc.nextDouble(), y = sc.nextDouble();// 求一元二次方程的根double t = (-v + Math.sqrt(x*y)) / x;// 保证t>=0t = Math.max(0, t);System.out.println(calc(y, x, v, t));}}
D. 游游的回文子串
因为n=1000,所以中心扩展就好了
- 同一个区域, 长度为n, 方案数n*(n+1)/2
- 以某个区域为中心,往两边扩展,则线性增长
import java.io.BufferedInputStream;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));int n = sc.nextInt();long[] arr = new long[n];for (int i = 0; i < arr.length; i++) {arr[i] = sc.nextInt();}long ans = 0;long mod = 10_0000_0007l;for (int i = 0; i < n; i++) {// 枚举某个区域long t = arr[i] * (arr[i] + 1) / 2;ans = (ans + t % mod) % mod;// 中心扩展for (int j = 1; i - j >= 0 && i + j < n; j++) {if (arr[i - j] != arr[i + j]) {// 长度不等,取最小,通过跳出ans = (ans + Math.min(arr[i - j], arr[i + j])) % mod;break;} else {ans = (ans + arr[i - j]) % mod;}}}System.out.println(ans);}}写在最后

相关文章:

牛客周赛 Round 10 解题报告 | 珂学家 | 三分模板 + 计数DFS + 回文中心扩展
前言 整体评价 T2真是一个折磨人的小妖精,写了两版DFS,第二版计数DFS才过。T3是三分模板,感觉也可以求导数。T4的数据规模才n1000,因此中心扩展的 O ( n 2 ) O(n^2) O(n2)当仁不让。 A. 游游的最长稳定子数组 滑窗经典题 从某个…...
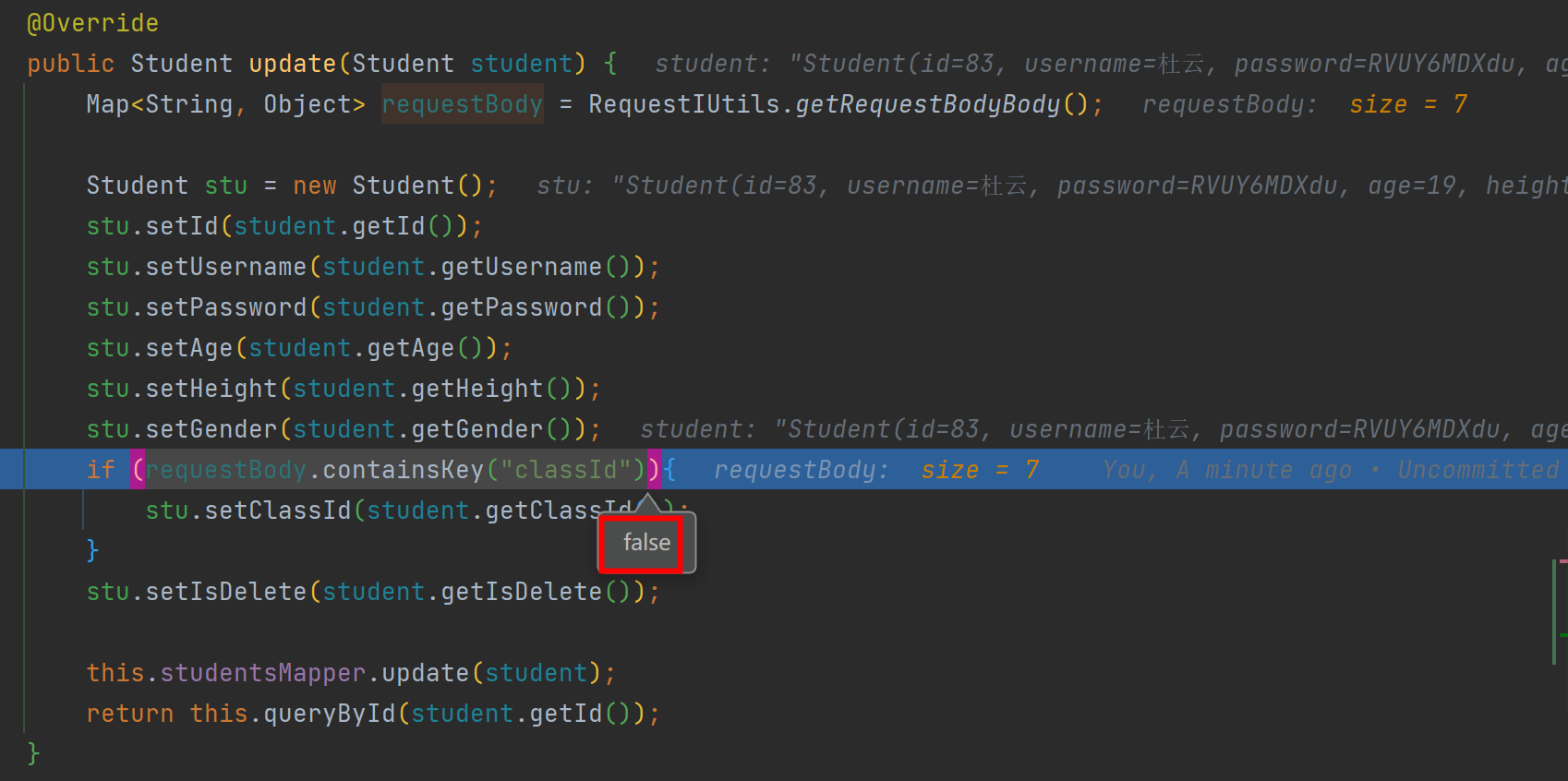
SpringBoot 更新业务场景下,如何区分null是清空属性值 还是null为vo属性默认值?
先看歧义现象 值为null 未传递此属性 所以此时如何区分null 时传递进来的的null,还是属性的默认值null? 引入方案 引入过滤器,中间截获requestBodyData并保存到HttpServletRequest,业务层从HttpServletRequest 获取到requestBodyData辅…...

【深度学习每日小知识】NLP 自然语言处理
自然语言处理 (NLP) 是人工智能 (AI) 的一个子领域,处理计算机和人类(自然)语言之间的交互。它涉及使用算法和统计模型使计算机能够理解、解释和生成人类语言。 NLP 是人工智能领域的重要工具,广泛应用于语言翻译、文本分类和聊天…...

一文理解Python选择语句
在编程领域中,条件判断和选择是非常基础而且重要的一个部分。Python 作为一种被广泛应用的编程语言,提供了多种选择语句来满足不同的条件判断需求。本文将深入探讨 Python 中的选择语句,包括 if 语句、elif 语句、else 语句、简写的条件表达式…...

MyBatis XML 映射文件中的 SQL 语句可以分为动态语句和静态语句
目录 静态查询: 动态查询: 静态更新: 动态更新: 静态删除: 动态删除: 动态语句和静态语句在 MyBatis 中的作用如下: 静态查询: 静态查询是指在 SQL 语句中执行固定的查询操作…...

Flask用于生产环境
Flask是一个用Python编写的轻量级Web应用框架,可以用于开发和部署Web服务。要安装Flask,您需要以下步骤: - 安装Python和pip,如果您还没有的话。 - 创建一个虚拟环境,以便隔离您的Flask应用程序和其他Python项目。 - …...

程序员如何向上管理,升职加薪
向上管理 多向领导展示自己的工作量。 解决完问题,可以把领导拉到群里,不然你解决了问题,领导都不知道。 积极向领导汇报,及时反馈任务进度,反馈遇到的问题。 要学会表现自己,光说不干假把式,…...

Microsoft Word 删除空行
Microsoft Word 删除空行 1. 删除空行1.1. 替换1.2. 段落标记 References 1. 删除空行 1.1. 替换 1.2. 段落标记 特殊格式 -> 段落标记 References [1] Yongqiang Cheng, https://yongqiang.blog.csdn.net/...

基于一次应用卡死问题所做的前端性能评估与优化尝试
问题背景 在上个月,由于客户反馈客户端卡死现象但我们远程却难以复现此现象,于是我们组织了一次现场上门故障排查,并希望基于此次观察与优化,为客户端开发提供一些整体的优化升级。当然,在尝试过程中,也发…...
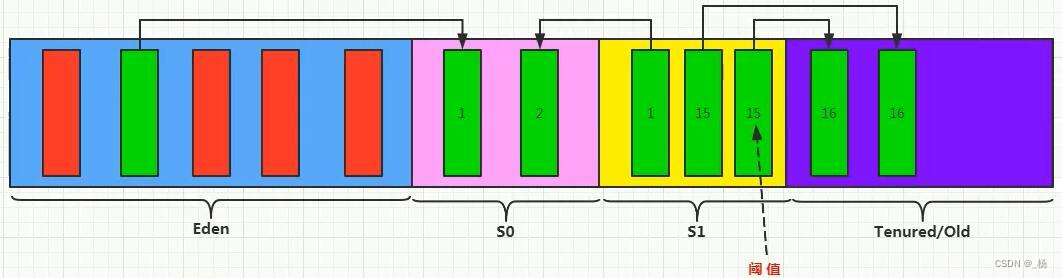
JVM(上)
目录 一、JVM概述 一、JVM作用 二、JVM整体组成部分 二、JVM结构-类加载 一、类加载子系统概述 二、类加载过程 1.加载 2.链接 3.初始化(类加载过程中的初始化) 三、类加载器分类 大致分两类: 细致分类: 四、双亲委派机制 五、打…...
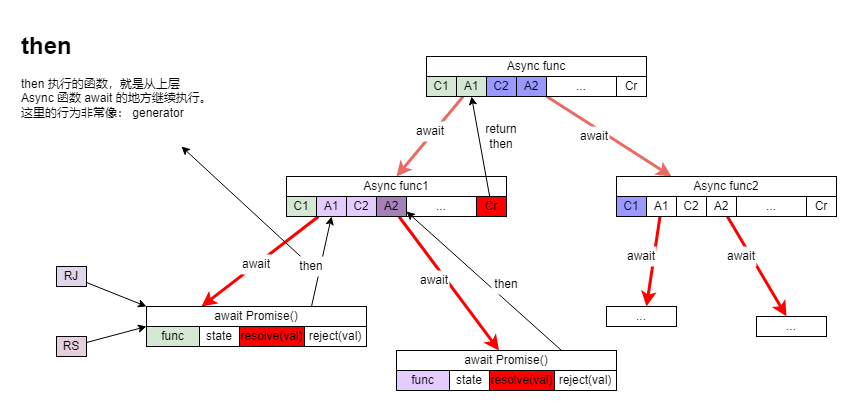
【js】js 异步机制详解 Generator / Async / Promise
三种语法功能放在一起,是因为他们都有相似特点: 维护某种状态在未来恢复状态并执行 本文重点回答以下几个问题: 为什么 Generator 和 Async 函数的 代码执行流 都可以简化成树形结构?async 函数为什么返回一个 promise…...

【动态规划】【数学】【C++算法】805 数组的均值分割
作者推荐 【动态规划】【数学】【C算法】18赛车 本文涉及知识点 动态规划 数学 805 数组的均值分割 给定你一个整数数组 nums 我们要将 nums 数组中的每个元素移动到 A 数组 或者 B 数组中,使得 A 数组和 B 数组不为空,并且 average(A) average(B)…...
:模型models)
Django笔记(五):模型models
首 Django中的模型对应数据库中的一张表格。 定义模型 player.py from django.db import modelsclass Player(models.Model):idx models.IntegerField(uniqueTrue)def __str__(self):return str(self.id)每个模型需要继承models类,如上Player模型定义了一个整形…...

一个golang小白使用vscode搭建Ununtu20.04下的go开发环境
文章目录 前言搭建go环境下载go安装包解压go压缩包完成安装配置环境变量编写一个helloword程序 安装VSCode插件安装智能提示插件安装go依赖包修改代理并重新安装依赖包 go.mod 和 go.workgo.modgo.work小试一下go.work 总结 前言 先交代一下背景,距离正式接触golan…...

【复现】Hytec Inter HWL 2511 SS路由器RCE漏洞_25
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 Hytec Inter HWL 2511 SS是日本Hytec Inter 公司的一款工业级 LTE 路由器,可用于远程数据传输,例如收集传…...
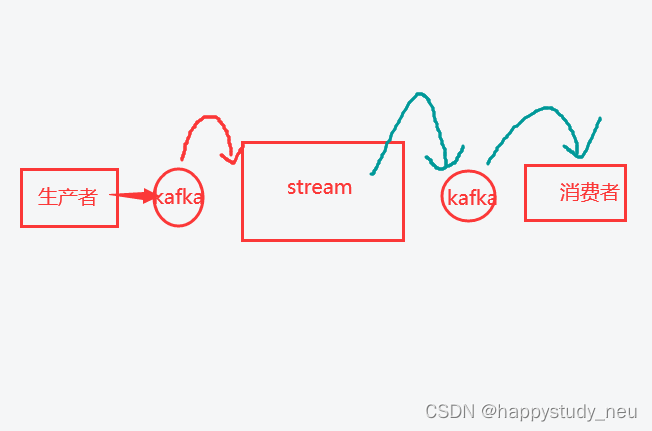
Kafka系列(四)
本文接kafka三,代码实践kafkaStream的应用,用来完成流式计算。 kafkastream 关于流式计算也就是实时处理,无时间概念边界的处理一些数据。想要更有性价比地和java程序进行结合,因此了解了kafka。但是本人阅读了kafka地官网&#…...
【Linux学习】进程信号
目录 十七.进程信号 导言 17.1 linux中的信号列表 17.2 标准信号与实时信号 17.3 信号的产生 17.3.1 通过终端按键产生信号 17.3.2 调用系统函数产生信号 17.3.3 软件条件产生信号 17.3.4 硬件异常产生信号 17.3.5 【补充】核心转储 Core Dump 17.4 信号的阻塞 17.4.1 信号相关…...
机器学习没那么难,Azure AutoML帮你简单3步实现自动化模型训练
在Machine Learning 这个领域,通常训练一个业务模型的难点并不在于算法的选择,而在于前期的数据清理和特征工程这些纷繁复杂的工作,训练过程中的问题在于参数的反复迭代优化。 AutoML 是 Azure Databricks 的一项功能,它自动的对…...
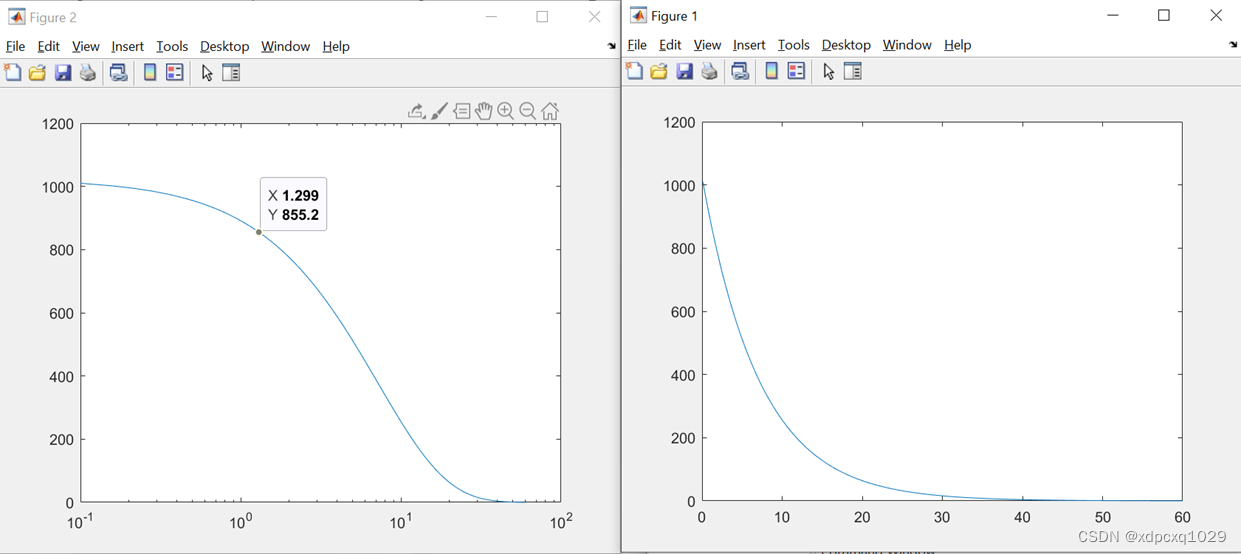
数学建模实战Matlab绘图
二维曲线、散点图 绘图命令:plot(x,y,’line specifiers’,’PropertyName’,PropertyValue) 例子:绘图表示年收入与年份的关系 ‘--r*’:--设置线型;r:设置颜色为红色;*节点型号 ‘linewidth’:设置线宽࿱…...

TypeError the JSON object must be str, bytes or bytearray, not ‘list‘
在使用python的jason库时,偶然碰到以下问题 TypeError: the JSON object must be str, bytes or bytearray, not ‘list’ 通过如下代码可复现问题 >>> a [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] >>> import json >>> ra json.loads(a) Trac…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
