计算机图形学07:有效边表法的多边形扫描转换

作者:非妃是公主
专栏:《计算机图形学》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 专栏系列文章
- 序
- 一、算法原理
- 二、OpenGL代码实现
- 三、效果展示
- the end……
专栏推荐
| 专栏名称 | 专栏地址 |
|---|---|
| 软件工程 | 专栏——软件工程 |
| 计算机图形学 | 专栏——计算机图形学 |
| 操作系统 | 专栏——操作系统 |
| 软件测试 | 专栏——软件测试 |
| 机器学习 | 专栏——机器学习 |
| 数据库 | 专栏——数据库 |
| 算法 | 专栏——算法 |
专栏系列文章
| 文章名称 | 文章地址 |
|---|---|
| 直线生成算法(DDA算法) | 计算机图形学01——DDA算法 |
| 中点BH算法绘制直线 | 计算机图形学02——中点BH算法 |
| 改进的中点BH算法 | 计算机图形学03——改进的中点BH算法 |
| 中点Bresenham画椭圆 | 计算机图形学04——中点BH绘制椭圆 |
| 中点BH算法绘制任意斜率直线 | 计算机图形学05——中点BH算法绘制任意斜率的直线 |
| 中点Bresenham画圆 | 计算机图形学06——中点BH算法画圆 |
| 有效边表法的多边形扫描转换 | 计算机图形学07——有效边表法绘制填充多边形 |
| 中点BH算法绘制抛物线 100x=y2100x = y^2100x=y2 | 计算机图形学08——中点BH绘制抛物线 |
| 二维观察之点的裁剪 | 计算机图形学09——二维观察之点裁剪 |
| 二维观察之线的裁剪 | 计算机图形学10——二维观察之线裁剪 |
| 二维观察之多边形的裁剪 | 计算机图形学11——二维观察之多边形裁剪 |
| 二维图形的几何变换 | 计算机图形学12——二维图形几何变换 |
| 三维图形的几何变换 | 计算机图形学13——三维图形几何变换 |
| 三维图形的投影变换 | 计算机图形学14——三维图形投影变换 |
序
计算机图形学(英语:computer graphics,缩写为CG)是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科,是计算机科学的一个分支领域,主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形,事实上同时包括了二维图形以及影像处理。
一、算法原理
有效边表法是X射线扫描转换的一种改进实现方式,相比于X射线方法,有效边表法由于不需要判断虚实交点,整体效率更高。
通过构造边表,然后随着X射线的移动不断地维护有效边表,通过两两配对边表中的有效边点亮像素,实现多边形的绘制。
具体原理如下:


排序方式按照x_ymin(y取到最小值的时候,x值的大小)排,x_ymin相等时按照1k\frac{1}{k}k1大小排,稍加思考会发现,正常情况下,不会出现相等情况。


由于配对原则,在顶点相交处,会影响到配对,采用的做法是,在影响配对的情况下进行ymax=ymax−1ymax=ymax-1ymax=ymax−1处理,通过此来保证在进行有效边交替的时候不会出现错误(即保证有效边表中的有效边数量为偶数)。

算法流程(本人在实现的时候,为编码符合自己的逻辑方式,先增加节点、再填充像素、填充后即检查是否需要删除如需要删除、最后进行各个有效边x_ymin属性的+1k+\frac{1}{k}+k1):

二、OpenGL代码实现
OpenGL代码实现如下:
// 有效边表法(AET)绘制填充多边形
void AETPolygon(vector<Point> pnts) {vector<Point>::iterator min_iter = min_element(pnts.begin(), pnts.end());vector<Point>::iterator max_iter = max_element(pnts.begin(), pnts.end());int min_y = min_iter->y;int max_y = max_iter->y;int dist = max_y - min_y + 1;vector<ETNode*> ET; // 边表for (int i = 0; i < dist; i++) {ET.push_back(new ETNode(0, 0, 0));}for (int i = 0; i < pnts.size(); i++) { // 建立边表// 建立边表节点的属性值double x_ymin, y_max, rev_k;if (pnts[i].y > pnts[(i + 1) % pnts.size()].y) { // 找出y最小值对应的x值x_ymin = pnts[(i + 1) % pnts.size()].x;y_max = pnts[i].y;// 如果为一个顶点的情况,y_max--if ((pnts[(i - 1 + pnts.size()) % pnts.size()].y - pnts[i].y) * (pnts[(i + 1 + pnts.size()) % pnts.size()].y - pnts[i].y) < 0) {y_max--;}}else {x_ymin = pnts[i].x;y_max = pnts[(i + 1) % pnts.size()].y;// 如果为一个顶点的情况,y_max--if ((pnts[(i + pnts.size()) % pnts.size()].y - pnts[i + 1].y) * (pnts[(i + 2 + pnts.size()) % pnts.size()].y - pnts[i + 1].y) < 0) {y_max--;}}// 计算 1/krev_k = (double)(pnts[(i + 1) % pnts.size()].x - pnts[i].x) / (pnts[(i + 1) % pnts.size()].y - pnts[i].y);// 计算 (1/斜率)ETNode* tmp = new ETNode(x_ymin, y_max, rev_k);ETNode* tmpFirstNode = ET[x_ymin - min_y];// 寻找合适的插入位置while (tmpFirstNode->next != nullptr && *(tmpFirstNode->next) < *tmp){tmpFirstNode = tmpFirstNode->next;}// 插入tmp->next = tmpFirstNode->next;tmpFirstNode->next = tmp;}// 建立活动边表ETNode* AET = new ETNode(0, 0, 0); // AET为头节点,不储存边表节点,后续节点才储存// 从下到上进行 x 射线扫描for (int i = min_y; i < max_y; i++) {ETNode* tmp_ETNode = ET[i - min_y];ETNode* tmp_AETNode = AET;while (tmp_ETNode->next != nullptr) {tmp_AETNode = AET;// 寻找AET中的插入位置while (tmp_AETNode->next != nullptr && *(tmp_AETNode->next) < *(tmp_ETNode->next)) {tmp_AETNode = tmp_AETNode->next;}//ET[i - min_y]->next = tmp_ETNode->next->next; 将tmp->next加入到 AET中//tmp_ETNode->next->next = tmp_AETNode->next;//tmp_AETNode->next = tmp_ETNode->next;//tmp_ETNode = ET[i - min_y];// 将tmp加入到 AET 中ETNode* tmp = new ETNode(tmp_ETNode->next->x_ymin, tmp_ETNode->next->y_max, tmp_ETNode->next->rev_k);tmp->next = tmp_AETNode->next;tmp_AETNode->next = tmp;tmp_ETNode = tmp_ETNode->next;}// 添加完以后进行画点tmp_AETNode = AET;while (tmp_AETNode->next != nullptr && tmp_AETNode->next->next != nullptr) {int fillBegin = (int)(tmp_AETNode->next->x_ymin + 0.5);int fillEnd = (int)(tmp_AETNode->next->next->x_ymin + 0.5);glColor3f(0.0f, 1.0f, 0.0f); // 设置颜色为绿色进行填充glBegin(GL_POINTS);for (int j = fillBegin; j <= fillEnd; j++) {glVertex2i(j, i);} glEnd();// 填充之后删除y=y_max的边if (i == tmp_AETNode->next->y_max || i == tmp_AETNode->next->next->y_max) {if (i == tmp_AETNode->next->y_max && i == tmp_AETNode->next->next->y_max) { // 删两个ETNode* del = tmp_AETNode->next;tmp_AETNode->next = tmp_AETNode->next->next;delete del;del = tmp_AETNode->next;tmp_AETNode->next = tmp_AETNode->next->next;delete del;}else if(i == tmp_AETNode->next->y_max) { // 删第一个ETNode* del = tmp_AETNode->next;tmp_AETNode->next = tmp_AETNode->next->next;delete del;tmp_AETNode = tmp_AETNode->next;}else { // 删第二个ETNode* del = tmp_AETNode->next->next;tmp_AETNode->next->next = tmp_AETNode->next->next->next;delete del;tmp_AETNode = tmp_AETNode->next;}continue;}tmp_AETNode = tmp_AETNode->next->next;}// 更新AET表中的x值tmp_AETNode = AET;while (tmp_AETNode->next != nullptr){tmp_AETNode->next->x_ymin += tmp_AETNode->next->rev_k;tmp_AETNode = tmp_AETNode->next;}}// 进行析构// 析构AETETNode* AEThead = AET;while (AEThead != nullptr) {ETNode* del = AEThead;AEThead = AEThead->next;delete del;}// 析构ETfor (int i = 0; i < ET.size(); i++) {ETNode* EThead = ET[i];while (EThead != nullptr) {ETNode* del = EThead;EThead = EThead->next;delete del;}}
}
三、效果展示
有效边表法的多边形扫描转换效果如下:



the end……
有效边表法的多边形扫描转换算法到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
😘😘😘 我是Cherries,一位计算机科班在校大学生,写博客用来记录自己平时的所思所想!
💞💞💞 内容繁杂,又才疏学浅,难免存在错误,欢迎各位大佬的批评指正!
👋👋👋 我们相互交流,共同进步!
注:本文由
非妃是公主发布于https://blog.csdn.net/myf_666,转载请务必标明原文链接:https://blog.csdn.net/myf_666/article/details/128226399
相关文章:

计算机图形学07:有效边表法的多边形扫描转换
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、算法原理二、…...

UNIX编程--Makefile入门
Makefile 文件命名和规则 文件命名 makefile 或者 Makefile Makefile 规则 一个 Makefile 文件中可以有一个或者多个规则目标 ... : 依赖 ...命令 (shell 命令)...目标:最终要生成的文件,伪目标除外依赖:生成目标所需的文件或是目…...
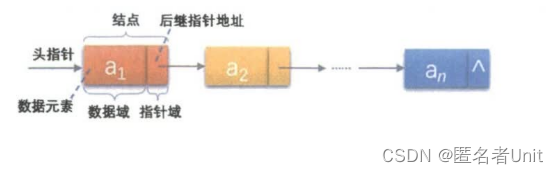
【数据结构初阶】手撕单链表
目录一.链表概念和结构二.单链表功能的实现1.打印单链表内容2.申请单链表节点3.头插和尾插4.头删和尾删5.单链表查找6.pos位置前后插入7.pos位置删除三.链表面试题剖析一.链表概念和结构 概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素…...

angular中http请求和传值
有关angular传值的相关内容 <number-info[subTitle]"customTitle"[total]"item.ENERGY_RATE %"[subTotal]"item.ENERGY_RATE_DIFF %"[status]"item.ENERGY_RATE_DIFF > 0 ? up : down">在number-info上面,会是一个delon/c…...
VSCode问题记录
20230304 - 0. 引言 这几年的编程方式还真是各种变化,从一开始直接VIM,到后面使用jupyter进行机器学习相关,然后再过渡到vim的形式并加以tmux批量化,最后去年使用了vscode作为IDE。随着工具的变化,那么很多习惯也都随…...

html基础学习
初识HTML HTML: 超文本标记语言 一.HTML的基本结构 根控制标记(头) 头控制标记(头) 标题 标题标记 头控制标记(尾) 网页显示区域(一般要实现的代码都在这里写) </body> 根控制标记(尾) 二.网页的基本标签 标题标签 <h1> 一级标题</h1> <…...
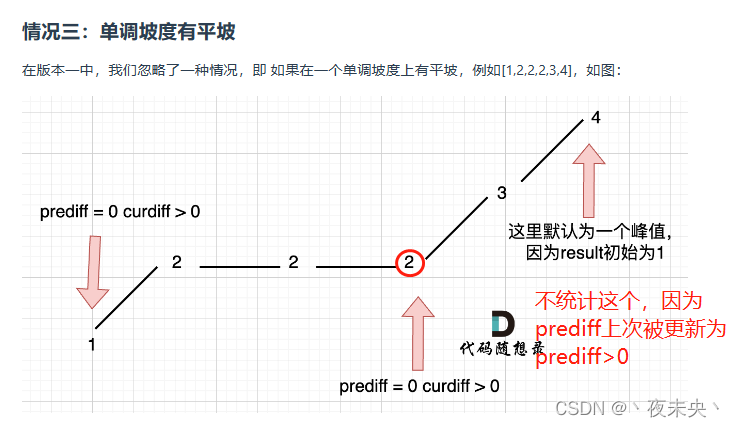
leetcode_贪心算法
贪心算法相关题简单题目455.分发饼干1005.K次取反后最大化的数组和860.柠檬水找零序列问题376.摆动序列法一:贪心法法二:动态规划单调递增的数字简化版本有点难度53.最大子序和贪心算法动态规划134.加油站968.监控二叉树两个维度权衡问题分发糖果406.根据…...
C语言每日一题】——杨氏矩阵
【C语言每日一题】——倒置字符串😎前言🙌杨氏矩阵🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简介…...
最佳iOS设备管理器imazing 2.16.9官网Mac/Windows下载电脑版怎么下载安装
imazing 2.16.9官网Mac/Windows下载电脑版是款针对苹果设备所打造的管理工具。iMazing为用户提供多种设备管理功能,每一位用户都能以自己的形式管理苹果设备。iMazing与苹果设备连接后,用户就可以轻松传输文件,浏览保存信息等。 应用介绍 iM…...

八大排序算法之堆排序的实现+经典TopK问题
目录 一.堆元素的上下调整接口 1.前言 2.堆元素向上调整算法接口 3.堆元素向下调整算法接口 二.堆排序的实现 1.空间复杂度为O(N)的堆排序(以排升序为例) 思路分析: 代码实现: 排序测试: 时空复杂度分析: 2. 空间复杂度为O(1)的堆排序(以排降序为例) 将数组arr调…...
使用AppSmith(PagePlug )低代码平台快速构建小程序应用实践
文章目录一、入门(一)介绍(二)功能特性(三)体验一下(四)参考教程二、使用Appsmith构建商城微信小程序(一)说明(二)应用配置࿰…...

第52章 短信验证服务和登录的后端定义实现
1 Services.Messages.SmsValidate using Core.Domain.Messages; using Data; using Microsoft.EntityFrameworkCore; namespace Services.Messages { /// <summary> /// 【短信验证服务--类】 /// <remarks> /// 摘要: /// 通过类中的方法成员实…...
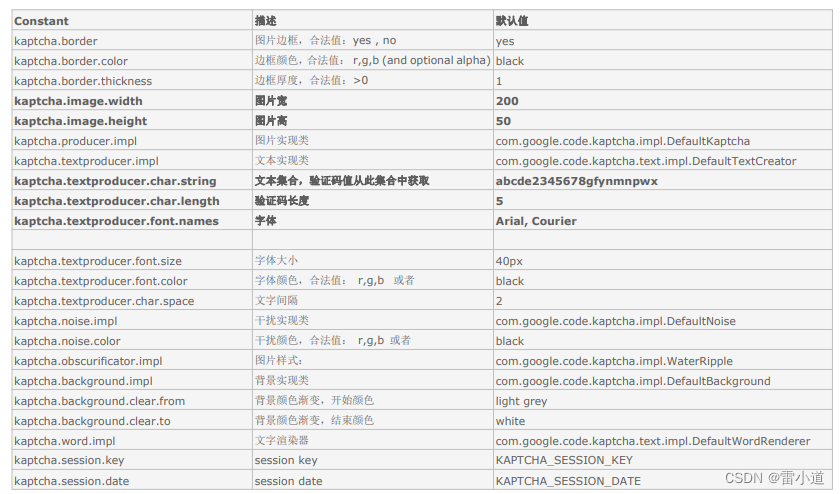
谷歌验证码的使用
1. 表单重复提交之验证码 1.1 表单重复提交三种常见情况 提交完表单。服务器使用请求转来进行页面跳转。这个时候,用户按下功能键 F5,就会发起最后一次的请求。造成表单重复提交问题。解决方法:使用重定向来进行跳转用户正常提交服务器&…...
- git的安装与配置)
Git学习入门(1)- git的安装与配置
title: git学习(1) - git的安装与配置CSDN: https://blog.csdn.net/jj6666djdbbd?typeblogBlog: https://helloylh.comGithub: https://github.com/luumodtags: gitabbrlink: 12001description: 本文主要讲解了git的安装,配置基本工作date: …...

【Python】使用Playwright断言方法验证网页和Web应用程序状态
作为测试框架,Playwright 提供了一系列断言方法,您可以使用它们来验证网页和 Web 应用程序的状态。在这篇博客中,田辛老师将介绍 Playwright 中可用的各种断言方法,并为每种方法提供示例。 assert page.url() expected_url &…...

libgdx导入blender模型
具体就是参考 官网 https://libgdx.com/wiki/graphics/3d/importing-blender-models-in-libgdx blender 教程可以看八个案例教程带你从0到1入门blender【已完结】 这里贴一下过程图。 1.初始环境搭建略过。 2.打开blender 选中摄像机和灯光,右键进行删除。 3.选中…...
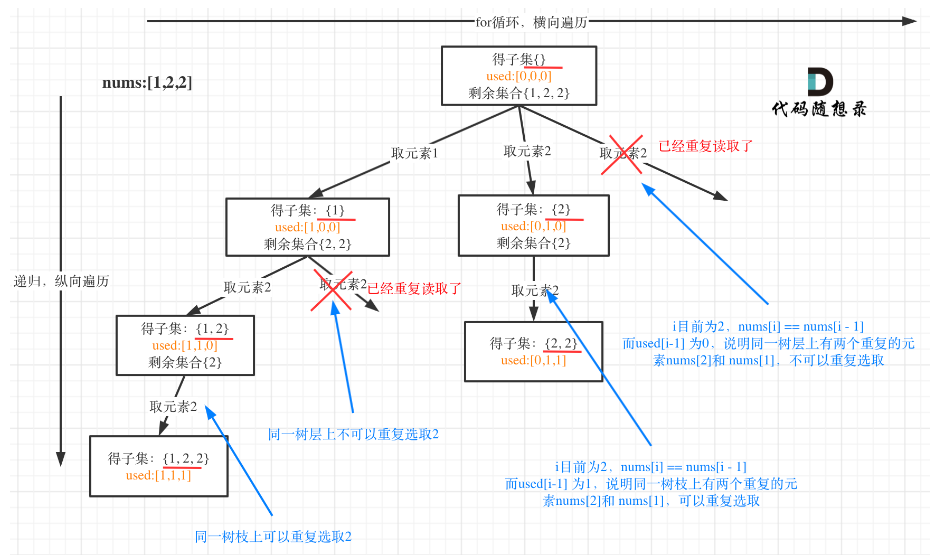
【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。回溯算法解决的经典问题:组合问题切割问题子集问题排列问题棋盘问题如何去理解回溯法?回溯法解决的问题都可以抽…...
centos安装rocketmq
centos安装rocketmq1 下载rocketmq二进制包2 解压二进制包3 修改broker.conf4 修改runbroker.sh和runserver.sh的JVM参数5 启动NameServer和Broker6 安装rockermq dashboard(可视化控制台)1 下载rocketmq二进制包 点击rocketmq二进制包下载地址,下载完成之后通过ft…...
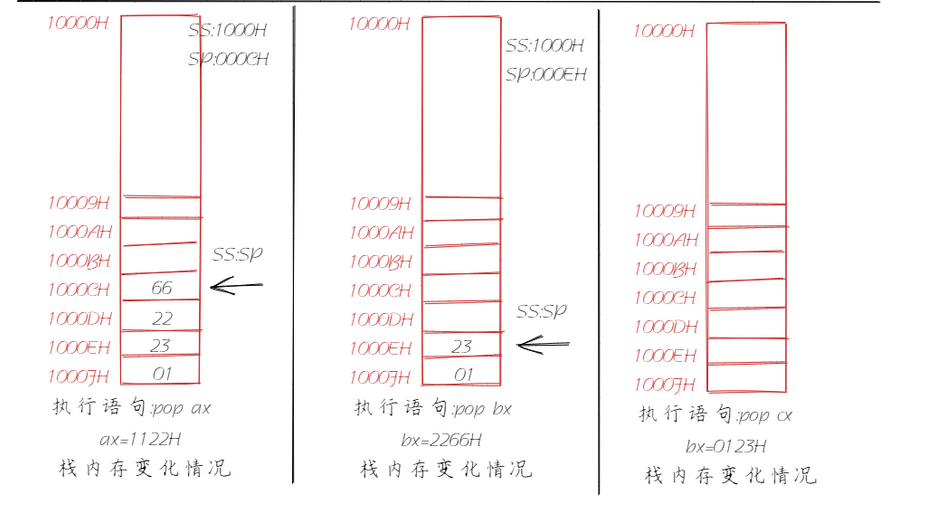
汇编语言程序设计(二)之寄存器
系列文章 汇编语言程序设计(一) 寄存器 在学习汇编的过程中,我们经常需要操作寄存器,那么寄存器又是什么呢?它是用来干什么的? 它有什么分类?又该如何操作?… 你可能会有许多的…...

华为OD机试Golang解题 - 单词接龙 | 独家
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

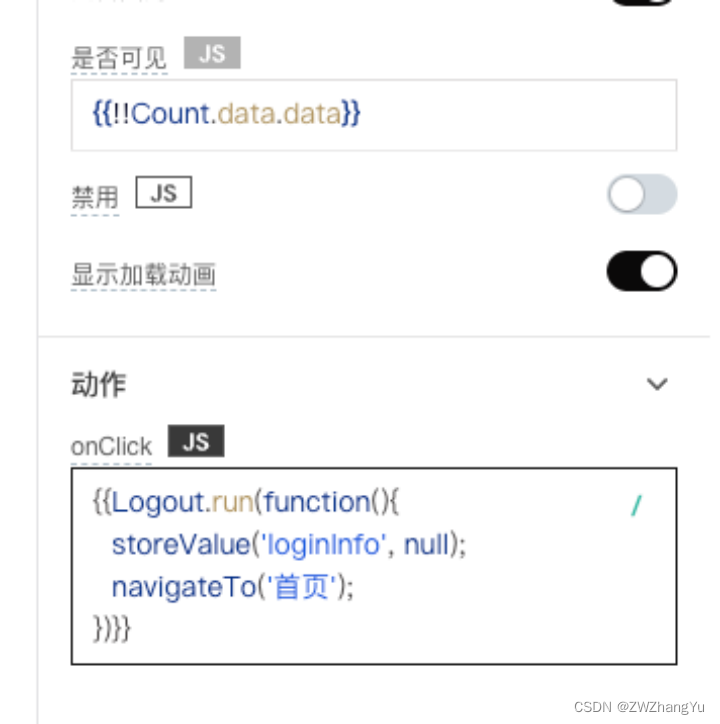
【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

