【线性代数与矩阵论】范数理论
范数理论
2023年11月16日
文章目录
- 范数理论
- 1. 向量的范数
- 2. 常用向量范数
- 3. 向量范数的等价性
- 4. 矩阵的范数
- 5. 常用的矩阵范数
- 6. 矩阵范数与向量范数的相容性
- 7. 矩阵范数诱导的向量范数
- 8. 由向量范数诱导的矩阵范数
- 9. 矩阵范数的酉不变性
- 10. 矩阵范数的等价性
- 11. 长方阵的范数
- 下链
1. 向量的范数
向量的长度也称为向量的二范数
[!quote]- 长度的定理
设 x , y , z ∈ C n , λ ∈ C {x,y,z\in \mathbb C^n \,\,,\,\, \lambda\in \mathbb C} x,y,z∈Cn,λ∈C
- 非负性:长度大于等于 0 {0} 0 ,仅当向量为 0 {0} 0 时取等。
- 齐次性: ∣ ∣ λ x ∣ ∣ = ∣ λ ∣ ⋅ ∣ ∣ x ∣ ∣ || \lambda x||=| \lambda| \cdot ||x|| ∣∣λx∣∣=∣λ∣⋅∣∣x∣∣。
- 三角不等式性: ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y||\le||x||+||y|| ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣。
定义 设 ∣ ∣ ⋅ ∣ ∣ {|| \cdot ||} ∣∣⋅∣∣ 是 C n { \mathbb C^n } Cn 上的一个泛函,满足
- 正定性: ∀ x ∈ C n {\forall x\in \mathbb C^n} ∀x∈Cn , ∣ ∣ x ∣ ∣ ≥ 0 {||x||\ge 0} ∣∣x∣∣≥0 ,且 ∣ ∣ x ∣ ∣ = 0 {||x||=0} ∣∣x∣∣=0 的充要条件是 x = 0 {x=0} x=0
- 齐次性: ∀ λ ∈ C {\forall \lambda \in \mathbb C} ∀λ∈C , x ∈ C n {x\in \mathbb C^n} x∈Cn , ∣ ∣ λ x ∣ ∣ = ∣ λ ∣ ⋅ ∣ ∣ x ∣ ∣ {|| \lambda x||=| \lambda| \cdot ||x||} ∣∣λx∣∣=∣λ∣⋅∣∣x∣∣
- 三角不等式性: ∀ x , y ∈ C n { \forall x,y\in \mathbb C^n} ∀x,y∈Cn , ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ {||x+y|| \le ||x||+||y||} ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣
则称 ∣ ∣ ⋅ ∣ ∣ {|| \cdot ||} ∣∣⋅∣∣ 是 C n { \mathbb C^n} Cn 上的一个向量范数。
定理 对任意 x , y ∈ C n {x,y\in \mathbb C^n} x,y∈Cn ,有
- ∣ ∣ − x ∣ ∣ = ∣ ∣ x ∣ ∣ {||-x||=||x||} ∣∣−x∣∣=∣∣x∣∣
- ∣ ∣ ∣ x ∣ ∣ − ∣ ∣ y ∣ ∣ ∣ ≤ ∣ ∣ x − y ∣ ∣ {|||x||-||y|||\le||x-y||} ∣∣∣x∣∣−∣∣y∣∣∣≤∣∣x−y∣∣
2. 常用向量范数
设 x ∈ C n {x\in \mathbb C^n} x∈Cn ,定义
- 向量的1范数:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1= \sum_{i=1}^{ n}|x_i| ∣∣x∣∣1=i=1∑n∣xi∣
为每个分量的绝对值之和。 - 向量的2范数:
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n ∣ x i ∣ 2 ||x||_2= \sqrt{ \sum_{i=1}^{ n}|x_i|^2} ∣∣x∣∣2=i=1∑n∣xi∣2
长度,欧几里得空间中的距离。 - 向量的 p {p} p 范数:
∣ ∣ x ∣ ∣ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p , 1 ≤ p ≤ + ∞ ||x||_p= (\sum_{i=1}^{ n}|x_i|^p)^{\frac{1}{p}} \,\,,\,\, 1\le p\le +\infty ∣∣x∣∣p=(i=1∑n∣xi∣p)p1,1≤p≤+∞ - 向量的无穷范数( p → ∞ {p\to\infty} p→∞ )
∣ ∣ x ∣ ∣ ∞ = max 1 ≤ i ≤ n ∣ x i ∣ ||x||_\infty= \max_{1\le i\le n}|x_i| ∣∣x∣∣∞=1≤i≤nmax∣xi∣
向量分量中绝对值最大的一个。
如果 A ∈ C n × n {A\in \mathbb C^{n \times n}} A∈Cn×n 是Hermit正定矩阵,则
∣ ∣ x ∣ ∣ A = x H A x , x ∈ C n {||x||_A= \sqrt{x^ \mathrm H Ax}\,\,,\,\, x\in \mathbb C^n} ∣∣x∣∣A=xHAx,x∈Cn
也是 C n { \mathbb C^n } Cn 上的向量范数。
3. 向量范数的等价性
定义 设 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 与 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 是 C n { \mathbb C^n} Cn 上两个向量范数,如果存在常数 c 1 , c 2 > 0 {c_1,c_2>0} c1,c2>0 使得 ∀ x ∈ C n { \forall x\in \mathbb C^n} ∀x∈Cn 有
c 1 ∣ ∣ x ∣ ∣ v 1 ≤ ∣ ∣ x ∣ ∣ v 2 ≤ c 2 ∣ ∣ x ∣ ∣ v 1 c_1||x||_{v1}\le||x||_{v2}\le c_2||x||_{v1} c1∣∣x∣∣v1≤∣∣x∣∣v2≤c2∣∣x∣∣v1
则称向量范数 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 与 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 等价。
理解 向量空间所有向量的 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 范数不会小于其 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 范数的 c 1 {c_1} c1 倍,也不会大于其 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 范数的 c 2 {c_2} c2 倍。同一个向量的两个范数要么同时大,要么同时小,但不一定成比例。
向量范数的等价实际上是等价关系
- 自身性:所有范数与自己等价
- 对称性:若 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 与 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 等价,则 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 与 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 等价
- 传递性:若 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 与 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 等价, ∣ ∣ ⋅ ∣ ∣ v 3 {|| \cdot ||_{v3}} ∣∣⋅∣∣v3 与 ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 等价,则 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1 与 ∣ ∣ ⋅ ∣ ∣ v 3 {|| \cdot ||_{v3}} ∣∣⋅∣∣v3 等价
定理 C n {\mathbb C^n} Cn 上的所有向量范数等价。
向量范数在向量序列极限概念上的应用
lim k → ∞ x ( k ) = x ⟺ lim k → ∞ ∣ ∣ x ( k ) − x ∣ ∣ = 0 \lim_{k\to\infty}x^{(k)}=x \iff \lim_{k\to\infty}||x^{(k)}-x||=0 k→∞limx(k)=x⟺k→∞lim∣∣x(k)−x∣∣=0
4. 矩阵的范数
定义 设 ∣ ∣ ⋅ ∣ ∣ {|| \cdot ||} ∣∣⋅∣∣ 是 C n × n { \mathbb C^{n \times n} } Cn×n 上的一个泛函,满足
- 正定性: ∀ A ∈ C n × n {\forall A\in \mathbb C^{n \times n}} ∀A∈Cn×n , ∣ ∣ x ∣ ∣ ≥ 0 {||x||\ge 0} ∣∣x∣∣≥0 ,且 ∣ ∣ x ∣ ∣ = 0 {||x||=0} ∣∣x∣∣=0 的充要条件是 x = 0 {x=0} x=0
- 齐次性: ∀ λ ∈ C {\forall \lambda \in \mathbb C} ∀λ∈C , A ∈ C n × n {A\in \mathbb C^{n \times n}} A∈Cn×n , ∣ ∣ λ A ∣ ∣ = ∣ λ ∣ ⋅ ∣ ∣ A ∣ ∣ {|| \lambda A||=| \lambda| \cdot ||A||} ∣∣λA∣∣=∣λ∣⋅∣∣A∣∣
- 三角不等式性: ∀ A , B ∈ C n × n { \forall A,B\in \mathbb C^{n \times n}} ∀A,B∈Cn×n , ∣ ∣ A + B ∣ ∣ ≤ ∣ ∣ A ∣ ∣ + ∣ ∣ B ∣ ∣ {||A+B|| \le ||A||+||B||} ∣∣A+B∣∣≤∣∣A∣∣+∣∣B∣∣
- 乘积不等式(相容性): ∀ A , B ∈ C n × n { \forall A,B\in \mathbb C^{n \times n}} ∀A,B∈Cn×n , ∣ ∣ A B ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ B ∣ ∣ {||AB|| \le ||A|| \cdot ||B||} ∣∣AB∣∣≤∣∣A∣∣⋅∣∣B∣∣
则称 ∣ ∣ ⋅ ∣ ∣ {|| \cdot ||} ∣∣⋅∣∣ 是 C n × n { \mathbb C^{n \times n}} Cn×n 上的一个矩阵范数。
5. 常用的矩阵范数
设 A = ( a i j ) ∈ C n × n {A=(a_{ij})\in \mathbb C^{n \times n}} A=(aij)∈Cn×n ,定义
- 矩阵的 m 1 {m_1} m1 范数
∣ ∣ A ∣ ∣ m 1 = ∑ i = 1 n ∑ j = 1 n ∣ a i j ∣ ||A||_{m1}= \sum_{i=1}^{ n}\sum_{j=1}^{ n}|a_{ij}| ∣∣A∣∣m1=i=1∑nj=1∑n∣aij∣ - 矩阵的 F {F} F 范数
∣ ∣ A ∣ ∣ F = ( ∑ i = 1 n ∑ j = 1 n ∣ a i j ∣ 2 ) 1 2 = tr ( A H A ) ||A||_F= (\sum_{i=1}^{ n}\sum_{j=1}^{ n}|a_{ij}|^2)^{ \frac{1}{2}}= \sqrt{\text{tr}(A^{\mathrm H}A) } ∣∣A∣∣F=(i=1∑nj=1∑n∣aij∣2)21=tr(AHA)
为每个元素平方再求和最后开方。 - 矩阵的 m ∞ {m_\infty} m∞ 范数
∣ ∣ A ∣ ∣ m ∞ = n ⋅ max 1 ≤ i , j ≤ n ∣ a i j ∣ ||A||_{m\infty}=n \cdot \max_{1\le i,j\le n}|a_{ij}| ∣∣A∣∣m∞=n⋅1≤i,j≤nmax∣aij∣
6. 矩阵范数与向量范数的相容性
定义 设 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_{m}} ∣∣⋅∣∣m 是 C n × n { \mathbb C^{n \times n} } Cn×n 上的矩阵范数, ∣ ∣ ⋅ ∣ ∣ v {|| \cdot ||_{v}} ∣∣⋅∣∣v 是 C n { \mathbb C^n} Cn 上的向量范数,如果 ∀ A ∈ C n × n , x ∈ C n { \forall A\in \mathbb C^{n \times n},x\in \mathbb C^n} ∀A∈Cn×n,x∈Cn
∣ ∣ A x ∣ ∣ v ≤ ∣ ∣ A ∣ ∣ m ⋅ ∣ ∣ x ∣ ∣ v ||Ax||_v\le ||A||_m \cdot ||x||_v ∣∣Ax∣∣v≤∣∣A∣∣m⋅∣∣x∣∣v
总是成立,则称矩阵范数 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_{m}} ∣∣⋅∣∣m 与向量范数 ∣ ∣ ⋅ ∣ ∣ v {|| \cdot ||_{v}} ∣∣⋅∣∣v 相容。下标m表示matrix,v表示vector。
定理
- 矩阵范数 ∣ ∣ ⋅ ∣ ∣ m 1 {|| \cdot ||_{m1}} ∣∣⋅∣∣m1 , ∣ ∣ ⋅ ∣ ∣ F {|| \cdot ||_{F}} ∣∣⋅∣∣F 分别与 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1, ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 相容
- 矩阵范数 ∣ ∣ ⋅ ∣ ∣ m ∞ {|| \cdot ||_{m\infty}} ∣∣⋅∣∣m∞ 与向量范数 ∣ ∣ ⋅ ∣ ∣ v 1 {|| \cdot ||_{v1}} ∣∣⋅∣∣v1, ∣ ∣ ⋅ ∣ ∣ v 2 {|| \cdot ||_{v2}} ∣∣⋅∣∣v2 , ∣ ∣ ⋅ ∣ ∣ v ∞ {|| \cdot ||_{v\infty}} ∣∣⋅∣∣v∞ 相容
7. 矩阵范数诱导的向量范数
对于任意的矩阵范数,都可以找到与之相容的向量范数。
设 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_m} ∣∣⋅∣∣m 是 C n × n { \mathbb C^{n \times n}} Cn×n 上一个矩阵范数,取 a ∈ C n {a\in \mathbb C^n} a∈Cn ,且 a ≠ 0 {a\ne0} a=0 ,定义
∣ ∣ x ∣ ∣ v = ∣ ∣ x a H ∣ ∣ m , x ∈ C n ||x||_v=||xa^ \mathrm H||_m \,\,,\,\, x\in \mathbb C^n ∣∣x∣∣v=∣∣xaH∣∣m,x∈Cn
可以证明,它是 C n { \mathbb C^n } Cn 上的向量范数,称为由矩阵范数 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_m} ∣∣⋅∣∣m 所诱导的向量范数。
定理 C n × n {\mathbb C^{n \times n} } Cn×n 上任意一矩阵范数 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_m} ∣∣⋅∣∣m 与他所诱导的向量范数 ∣ ∣ ⋅ ∣ ∣ v {|| \cdot ||_v} ∣∣⋅∣∣v 相容。
∣ ∣ A x ∣ ∣ v = ∣ ∣ ( A x ) a H ∣ ∣ m = ∣ ∣ A ( x a H ) ∣ ∣ m ≤ ∣ ∣ A ∣ ∣ m ∣ ∣ ( x a H ) ∣ ∣ m = ∣ ∣ A ∣ ∣ m ∣ ∣ x ∣ ∣ v \begin{align*} ||Ax||_v=&||(Ax)a^ \mathrm H||_m=||A(xa^ \mathrm H)||_m \\ \\ \le&||A||_m||(xa^ \mathrm H)||_m=||A||_m||x||_v \end{align*} ∣∣Ax∣∣v=≤∣∣(Ax)aH∣∣m=∣∣A(xaH)∣∣m∣∣A∣∣m∣∣(xaH)∣∣m=∣∣A∣∣m∣∣x∣∣v
8. 由向量范数诱导的矩阵范数
设 ∣ ∣ ⋅ ∣ ∣ v {|| \cdot ||_v} ∣∣⋅∣∣v 是 C n { \mathbb C^n} Cn 上一个向量范数,定义
∣ ∣ A ∣ ∣ m = max ∣ ∣ x ∣ ∣ v = 1 ∣ ∣ A x ∣ ∣ v = max x ≠ 0 ∣ ∣ A x ∣ ∣ v ∣ ∣ x ∣ ∣ v , A ∈ C n × n ||A||_m=\max_{||x||_v=1}||Ax||_v=\max_{x\ne 0} \frac{||Ax||_v}{||x||_v} \,\,,\,\, A\in \mathbb C^{n \times n} ∣∣A∣∣m=∣∣x∣∣v=1max∣∣Ax∣∣v=x=0max∣∣x∣∣v∣∣Ax∣∣v,A∈Cn×n
( ∣ ∣ A x ∣ ∣ v ∣ ∣ x ∣ ∣ v = ∣ ∣ 1 ∣ ∣ x ∣ ∣ v A x ∣ ∣ v = ∣ ∣ A ( 1 ∣ ∣ x ∣ ∣ v x ) ∣ ∣ v ) \bigg( \frac{||Ax||_v}{||x||_v}= \bigg| \bigg| \frac{1}{||x||_{v}}Ax \bigg| \bigg| _{v}= \bigg| \bigg| A \bigg( \frac{1}{||x||_{v }}x \bigg) \bigg| \bigg|_v \bigg) (∣∣x∣∣v∣∣Ax∣∣v= ∣∣x∣∣v1Ax v= A(∣∣x∣∣v1x) v)
称为由向量范数 ∣ ∣ ⋅ ∣ ∣ v { || \cdot ||_{ v}} ∣∣⋅∣∣v 所诱导的矩阵范数(从属范数)。
定理 C n {\mathbb C^{n} } Cn 上任意一向量范数 ∣ ∣ ⋅ ∣ ∣ v {|| \cdot ||_v} ∣∣⋅∣∣v 与他所诱导的矩阵范数 ∣ ∣ ⋅ ∣ ∣ m {|| \cdot ||_m} ∣∣⋅∣∣m 相容。
将向量范数 ∣ ∣ ⋅ ∣ ∣ 1 { || \cdot ||_{1 }} ∣∣⋅∣∣1, ∣ ∣ ⋅ ∣ ∣ 2 { || \cdot ||_{2 }} ∣∣⋅∣∣2, ∣ ∣ ⋅ ∣ ∣ ∞ { || \cdot ||_{\infty }} ∣∣⋅∣∣∞ 诱导的矩阵范数分别记为 ∣ ∣ ⋅ ∣ ∣ 1 { || \cdot ||_{1 }} ∣∣⋅∣∣1, ∣ ∣ ⋅ ∣ ∣ 2 { || \cdot ||_{2 }} ∣∣⋅∣∣2, ∣ ∣ ⋅ ∣ ∣ ∞ { || \cdot ||_{\infty }} ∣∣⋅∣∣∞ ,则有在同济大学《数值分析》或者一些数值分析速通网课里面提到的矩阵范数。
列范数
- 矩阵的1范数(列和范数)
∣ ∣ A ∣ ∣ 1 = max 1 ≤ j ≤ n ∑ i = 1 n ∣ a i j ∣ ||A||_1=\max_{1\le j\le n} \sum_{i=1}^{ n}|a_{ij}| ∣∣A∣∣1=1≤j≤nmaxi=1∑n∣aij∣
为每列元素绝对值之和的最大的一个。 - 矩阵的2范数
∣ ∣ A ∣ ∣ 2 = ( A T A 的最大特征值 ) ||A||_2= \sqrt{(A^ \mathrm TA的最大特征值)} ∣∣A∣∣2=(ATA的最大特征值)
行范数 - 矩阵的 ∞ {\infty} ∞ 范数(行和范数)
∣ ∣ A ∣ ∣ ∞ = max 1 ≤ i ≤ n ∑ j = 1 n ∣ a i j ∣ ||A||_\infty=\max_{1\le i\le n} \sum_{j=1}^{ n}|a_{ij}| ∣∣A∣∣∞=1≤i≤nmaxj=1∑n∣aij∣
为每行元素绝对值之和的最大的一个。 - 矩阵的 F {F} F 范数也是行范数。
相容关系如下:
∣ ∣ A x ∣ ∣ 1 ≤ ∣ ∣ A ∣ ∣ 1 ⋅ ∣ ∣ x ∣ ∣ 1 ∣ ∣ A x ∣ ∣ ∞ ≤ ∣ ∣ A ∣ ∣ ∞ ⋅ ∣ ∣ x ∣ ∣ ∞ ∣ ∣ A x ∣ ∣ 2 ≤ ∣ ∣ A ∣ ∣ 2 ⋅ ∣ ∣ x ∣ ∣ 2 ∣ ∣ A x ∣ ∣ 2 ≤ ∣ ∣ A ∣ ∣ F ⋅ ∣ ∣ x ∣ ∣ 2 \begin{align*} ||Ax||_1\le& ||A||_1 \cdot ||x||_1\\ \\ ||Ax||_\infty\le& ||A||_\infty \cdot ||x||_\infty\\ \\ ||Ax||_2\le& ||A||_2 \cdot ||x||_2\\ \\ ||Ax||_2\le& ||A||_F \cdot ||x||_2\\ \\ \end{align*} ∣∣Ax∣∣1≤∣∣Ax∣∣∞≤∣∣Ax∣∣2≤∣∣Ax∣∣2≤∣∣A∣∣1⋅∣∣x∣∣1∣∣A∣∣∞⋅∣∣x∣∣∞∣∣A∣∣2⋅∣∣x∣∣2∣∣A∣∣F⋅∣∣x∣∣2
9. 矩阵范数的酉不变性
设 A ∈ C n × n {A\in \mathbb C^{n \times n} } A∈Cn×n ,则
- ∣ ∣ A H ∣ ∣ F = ∣ ∣ A ∣ ∣ F {||A^ \mathrm H||_F = || A ||_{F }} ∣∣AH∣∣F=∣∣A∣∣F , ∣ ∣ A H ∣ ∣ 2 = ∣ ∣ A ∣ ∣ 2 { || A^ \mathrm H ||_{ 2} = || A ||_{ 2}} ∣∣AH∣∣2=∣∣A∣∣2
- 酉不变性 对任意酉矩阵 U , V ∈ C n × n {U,V \in \mathbb C^{n \times n} } U,V∈Cn×n
∣ ∣ U A ∣ ∣ F = ∣ ∣ A V ∣ ∣ F = ∣ ∣ U A V ∣ ∣ F , ∣ ∣ U A ∣ ∣ 2 = ∣ ∣ A V ∣ ∣ 2 = ∣ ∣ U A V ∣ ∣ 2 || UA ||_{ F}= || AV ||_{ F} = || UAV ||_{ F} \,\,,\,\, || UA ||_{ 2}= || AV ||_{ 2}= || UAV ||_{ 2} ∣∣UA∣∣F=∣∣AV∣∣F=∣∣UAV∣∣F,∣∣UA∣∣2=∣∣AV∣∣2=∣∣UAV∣∣2 - 若 A {A} A 是正规矩阵,且 λ 1 , λ 2 , ⋅ , λ n { \lambda_1, \lambda_2, \cdot , \lambda_n} λ1,λ2,⋅,λn 是 A {A} A 的 n {n} n 个特征值,则
∣ ∣ A ∣ ∣ 2 = max k ∣ λ k ∣ || A ||_{2 }= \max_k | \lambda_k | ∣∣A∣∣2=kmax∣λk∣
即如果 A {A} A 正规, A {A} A 的 2 {2} 2 范数是它最大特征值的绝对值(与谱半径相等)。
10. 矩阵范数的等价性
定理 C n × n {\mathbb C^{n \times n} } Cn×n 上所有矩阵范数等价。
11. 长方阵的范数
矩阵范数的相容性 ∀ A ∈ C m × n {\forall A\in \mathbb C^{m \times n}} ∀A∈Cm×n , B ∈ C n × l {B\in \mathbb C^{n \times l}} B∈Cn×l
∣ ∣ A B ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ B ∣ ∣ || AB ||_{ }\le || A ||_{ } \cdot || B ||_{ } ∣∣AB∣∣≤∣∣A∣∣⋅∣∣B∣∣
矩阵范数与向量范数的相容性 ∀ A ∈ C m × n {\forall A\in \mathbb C^{m \times n}} ∀A∈Cm×n , x ∈ C n {x\in \mathbb C^{n}} x∈Cn
∣ ∣ A x ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ x ∣ ∣ || Ax ||_{ }\le || A ||_{ } \cdot || x ||_{ } ∣∣Ax∣∣≤∣∣A∣∣⋅∣∣x∣∣
从属范数
∣ ∣ A ∣ ∣ = max ∣ ∣ x ∣ ∣ v = 1 ∣ ∣ A x ∣ ∣ v = max x ≠ 0 ∣ ∣ A x ∣ ∣ v ∣ ∣ x ∣ ∣ v , A ∈ C m × n || A ||_{ }= \max_{|| x ||_{v }=1} || Ax ||_{ v}=\max_{x\ne 0} \frac{|| Ax ||_{ v}}{|| x ||_{ v}} \,\,,\,\, A\in \mathbb C^{m \times n} ∣∣A∣∣=∣∣x∣∣v=1max∣∣Ax∣∣v=x=0max∣∣x∣∣v∣∣Ax∣∣v,A∈Cm×n
其中 ∣ ∣ A x ∣ ∣ v { || Ax ||_{v }} ∣∣Ax∣∣v 是 C m { \mathbb C^m } Cm 上的范数, ∣ ∣ x ∣ ∣ v { || x ||_{ v}} ∣∣x∣∣v 是 C n { \mathbb C^n} Cn 上的范数。
对任意 A ∈ C m × n {A\in \mathbb C^{m \times n} } A∈Cm×n ,常用的矩阵范数有:
- 长方阵的 m 1 {m_1} m1 范数
∣ ∣ A ∣ ∣ m 1 = ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ ||A||_{m1}= \sum_{i=1}^{ m}\sum_{j=1}^{ n}|a_{ij}| ∣∣A∣∣m1=i=1∑mj=1∑n∣aij∣ - 长方阵的 F {F} F 范数
∣ ∣ A ∣ ∣ F = ( ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ 2 ) 1 2 = tr ( A H A ) ||A||_F= (\sum_{i=1}^{ m}\sum_{j=1}^{ n}|a_{ij}|^2)^{ \frac{1}{2}}= \sqrt{\text{tr}(A^{\mathrm H}A) } ∣∣A∣∣F=(i=1∑mj=1∑n∣aij∣2)21=tr(AHA)
为每个元素平方再求和最后开方。 - 长方阵的 M {M} M 范数或最大范数
∣ ∣ A ∣ ∣ M = max { n , m } ⋅ max 1 ≤ i , j ≤ n ∣ a i j ∣ ||A||_{M}=\max \lbrace n,m \rbrace \cdot \max_{1\le i,j\le n}|a_{ij}| ∣∣A∣∣M=max{n,m}⋅1≤i,j≤nmax∣aij∣ - 长方阵的 G {G} G 范数或几何平均范数
∣ ∣ A ∣ ∣ G = m n ⋅ max i , j ∣ a i j ∣ || A ||_{ G}= \sqrt{mn} \cdot \max_{i,j}|a_{ij}| ∣∣A∣∣G=mn⋅i,jmax∣aij∣ - 长方阵的 1 {1} 1 范数或列和范数
∣ ∣ A ∣ ∣ 1 = max 1 ≤ j ≤ n ∑ i = 1 m ∣ a i j ∣ || A ||_{ 1}=\max_{1\le j\le n} \sum_{i=1}^{ m}|a_{ij}| ∣∣A∣∣1=1≤j≤nmaxi=1∑m∣aij∣ - 长方阵的 2 {2} 2 范数或谱范数
∣ ∣ A ∣ ∣ 2 = ( A T A 的最大特征值 ) || A ||_{ 2}= \sqrt{(A^ \mathrm TA的最大特征值)} ∣∣A∣∣2=(ATA的最大特征值) - 长方阵的 ∞ {\infty} ∞ 范数或行和范数
∣ ∣ A ∣ ∣ ∞ = max 1 ≤ i ≤ m ∑ j = 1 n ∣ a i j ∣ || A ||_{\infty }= \max_{1\le i\le m} \sum_{j=1}^{ n} |a_{ij}| ∣∣A∣∣∞=1≤i≤mmaxj=1∑n∣aij∣
部分性质:
- F {F} F 范数, 2 {2} 2 范数,酉不变
- m 1 {m_1} m1 范数与向量 1 {1} 1 范数相容
- F {F} F 范数、 G {G} G 范数与向量 2 {2} 2 范数相容
- M {M} M 范数与向量 1 {1} 1, 2 {2} 2, ∞ {\infty} ∞ 范数相容
- 矩阵 1 {1} 1, 2 {2} 2, ∞ {\infty} ∞ 范数分别由向量 1 {1} 1, 2 {2} 2, ∞ {\infty} ∞ 范数导出,从而相容
- C m × n {\mathbb C^{m \times n} } Cm×n 上所有范数等价
下链
相关文章:

【线性代数与矩阵论】范数理论
范数理论 2023年11月16日 文章目录 范数理论1. 向量的范数2. 常用向量范数3. 向量范数的等价性4. 矩阵的范数5. 常用的矩阵范数6. 矩阵范数与向量范数的相容性7. 矩阵范数诱导的向量范数8. 由向量范数诱导的矩阵范数9. 矩阵范数的酉不变性10. 矩阵范数的等价性11. 长方阵的范数…...

【C++】priority_queue模拟实现过程中值得注意的点
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》《算法》 🌝每一个不曾起舞的日子,都是对生命的辜负 前言 本篇文章旨在记录博主在模…...
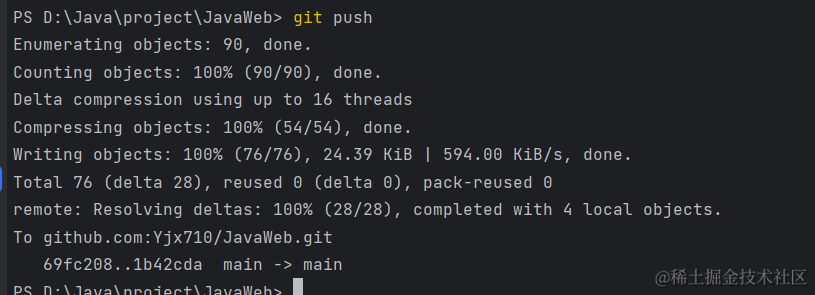
Git提交 ssh: connect to host github.com port 22: Connection timed out解决方案
你们好,我是金金金。 场景 之前都是好好的,不知道今天为什么提交代码就这样了 排查 根据英文可以看出,ssh端口号被拒绝了,22号端口不行,那就换一个端口 造成error的原因 ssh端口被拒绝 解决 找到.ssh文件ÿ…...

Java调用WebService接口,SOAP协议HTTP请求返回XML对象
Java调用Web service接口SOAP协议HTTP请求,解析返回的XML字符串: 1. 使用Java的HTTP库发送SOAP请求,并接收返回的响应。 可以使用Java的HttpURLConnection、Apache HttpClient等库。 2. 将返回的响应转换为字符串。 3. 解析XML字符串&…...

Django框架二
一、模型层及ORM 1.模型层定义 负责跟数据库之间进行通信 2.Django配置mysql 安装mysqlclient,mysqlclient版本最好在13.13以上 pip3 install mysqlclient DATABASES {default: {ENGINE: django.db.backends.mysql,NAME: "mysite1",USER:root,PASSWO…...

工业相机与镜头参数及选型
文章目录 1、相机成像系统模型1.1 视场1.2 成像简化模型 2、工业相机参数2.1 分辨率2.2 靶面尺寸2.3 像元尺寸2.4 帧率/行频2.5 像素深度2.6 动态范围2.7 信噪比2.8 曝光时间2.9 相机接口 3、工业镜头参数3.1 焦距3.2 光圈3.3 景深3.4 镜头分辨率3.5 工作距离(Worki…...
VSCode使用Makefile Tools插件开发C/C++程序
提起Makefile,可能有人会觉得它已经过时了,毕竟现在有比它更好的工具,比如CMake,XMake,Meson等等,但是在Linux下很多C/C源码都是直接或者间接使用Makefile文件来编译项目的,可以说Makefile是基石…...

用C语言验证“三门定理”
#include <stdio.h> #include <stdbool.h> #include <stdlib.h> #include <time.h>// 一个源自博弈论的数学游戏问题: // 参赛者会看见三扇门, // 其中一扇门的里面有一辆汽车, // 选中里面是汽车的那扇门࿰…...
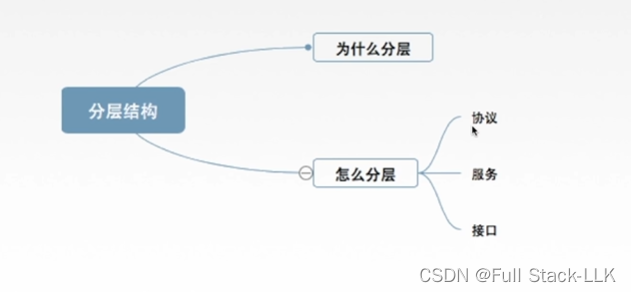
计算机网络-分层结构,协议,接口,服务
文章目录 总览为什么要分层怎样分层正式认识分层概念小结 总览 为什么要分层 发送文件前要做的准备工作很多 把这个准备工作分层小问题解决,也就分层解决 怎样分层 每层相互独立,每层做的工作不同 界面自然清晰,层与层之间的接口能够体现…...

前端开发 2: CSS
在前端开发中,CSS(层叠样式表)是一种用于描述网页样式的语言。它控制着网页的布局、颜色、字体等外观效果。在本篇博客中,我将为你介绍 CSS 的基础知识和常用技巧,帮助你更好地掌握前端开发中的样式设计。 CSS 基础知…...
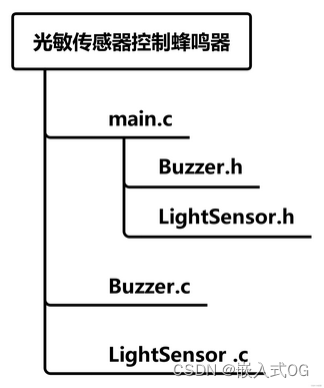
嵌入式-Stm32-江科大基于标准库的GPIO4个小实验
文章目录 一 、硬件介绍二 、实验:LED闪烁、LED流水灯、蜂鸣器提示2.1 需求1:面包板上的LED以1s为周期进行闪烁。亮0.5s,灭0.5s.....2.2 需求2: 8个LED实现流水灯2.3 需求3:蜂鸣器不断地发出滴滴、滴滴.....的提示音。蜂鸣器低电平触发。 三、…...
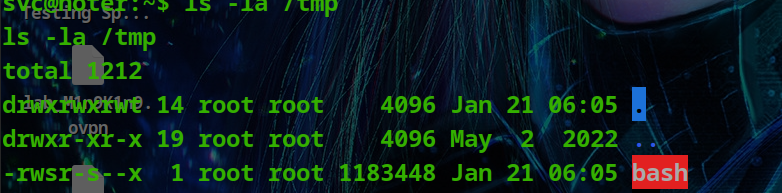
HackTheBox - Medium - Linux - Noter
Noter Noter 是一种中型 Linux 机器,其特点是利用了 Python Flask 应用程序,该应用程序使用易受远程代码执行影响的“节点”模块。由于“MySQL”守护进程以用户“root”身份运行,因此可以通过利用“MySQL”的用户定义函数来利用它来获得RCE并…...
Uniapp多选Popup(弹出层)
uniapp中多选组件很少,故个人简单开发了一个,可简单使用,也可根据个人需求稍微改进 支持的功能 单选多选(默认)限制选择数量默认选中禁用选项 属性说明 属性默认值说明singlefalsetrue为开启单选,否则为…...

什么是网络安全?网络安全概况
网络安全涉及保护我们的计算机网络、设备和数据免受未经授权的访问或破坏。 这个领域包括多种技术、过程和控制措施,旨在保护网络、设备和数据免受攻击、损害或未授权访问。网络安全涉及多个方面,包括但不限于信息安全、应用程序安全、操作系统安全等 …...
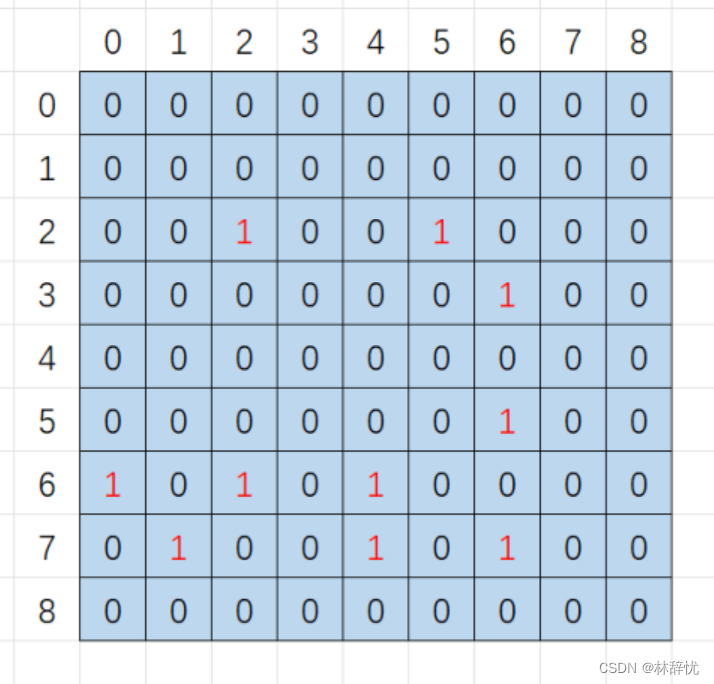
c语言小游戏之扫雷
目录 一:游戏设计理念及思路 二:初步规划的游戏界面 三:开始扫雷游戏的实现 注:1.创建三个文件,test.c用来测试整个游戏的运行,game.c用来实现扫雷游戏的主体,game.h用来函数声明和包含头文…...

如何本地安装Python Flask并结合内网穿透实现远程开发
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

在线App封装技术:HTML5的新生命
HTML5封装的魅力所在HTML5带来了丰富的多媒体功能、地理位置服务、离线存储等特性,使得Web应用的体验更加接近原生App。封装HTML5到App中,可以大大缩短开发周期,降低开发成本,并且一次编写,多平台运行,极大…...
Spring Boot 4.0:构建云原生Java应用的前沿工具
目录 前言 Spring Boot简介 Spring Boot 的新特性 1. 支持JDK 17 2. 集成云原生组件 3. 响应式编程支持 4. 更强大的安全性 5. 更简化的配置 Spring Boot 的应用场景 1. 云原生应用开发 2. 响应式应用程序 3. 安全性要求高的应用 4. JDK 17的应用 总结 作…...
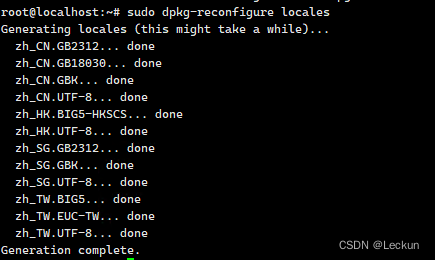
Debian系统写Mysql时中文出现乱码无法定入的问题解决方案
原因是操作系统可能精简安装,没有GBK字符集,只有UTF8在转换或使用的时候有问题。 使用locale -a查看系统支持的字符集。正常的比较全的字符集的操作系统如下: 有问题的操作系统字符集如下: 解决方案: 步骤1&#…...
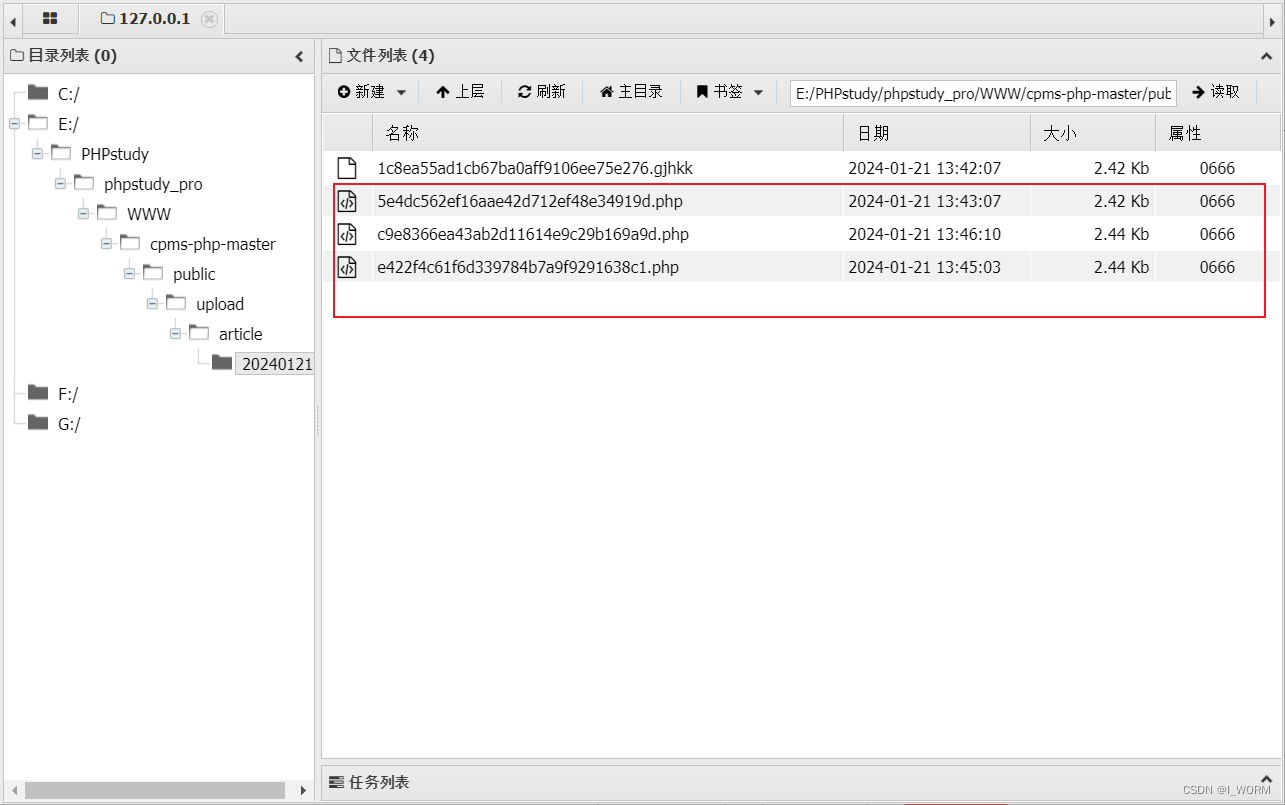
CPMS靶场练习
关键:找到文件上传点,分析对方验证的手段 首先查看前端发现没有任何上传的位置,找到网站的后台,通过弱口令admin 123456可以进入 通过查看网站内容发现只有文章列表可以进行文件上传;有两个图片上传点 图片验证很严格…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
