双端Diff算法
双端Diff算法
双端Diff算法指的是,在新旧两组子节点的四个端点之间分别进行比较,并试图找到可复用的节点。相比简单Diff算法,双端Diff算法的优势在于,对于同样的更新场景,执行的DOM移动操作次数更少。
- 简单 Diff 算法(单向 Diff):
-
工作原理:简单 Diff 算法从一个序列的起始位置开始,逐个比较元素,找出不同之处。
-
特点:
-
顺序性:仅从一个方向进行比较,一旦发现不同之处,就会停止继续比较。
-
复杂度:时间复杂度为 O(n),其中 n 是序列的长度。
-
结果不唯一:因为只按照一个方向进行比较,可能会忽略一些潜在的更优的匹配方式。
-
- 双端 Diff 算法(双向 Diff):
- 工作原理:双端 Diff 算法同时从两个序列的起始位置开始,向中间移动,逐个比较元素,找出不同之处。
- 特点:
- 双向性:同时从两个方向进行比较,可以更全面地考虑匹配情况。
- 优化效率:通过跳过相同的前缀和后缀部分,减少了比较的次数,提高了效率。
- 复杂度:时间复杂度为 O(n+m),其中 n 和 m 分别是两个序列的长度。
- 结果更准确:考虑了更多的匹配可能性,得到更准确的差异结果。
双端Diff算法的比较方式




双端Diff算法是一种同时对新旧两组子节点的两个端点进行比较的算法,因此我们需要四个索引值,分别指向新旧两组节点的端点。
function patchChildren(n1, n2, container) {if (typeof n2.children === 'string') {// 省略部分代码} else if (Array.isArray(n2.children)) {// 封装 patchKeyedChildren 函数处理两组子节点patchKeyedChildren(n1, n2, container);} else {// 省略部分代码}
}
function patchKeyedChildren(n1, n2, container) {const oldChildren = n1.children;const newChildren = n2.children;// 四个索引值let oldStartIdx = 0;let oldEndIdx = oldChildren.length - 1;let newStartIdx = 0;let newEndIdx = newChildren.length - 1;// 四个索引指向的 vnode 节点let oldStartVNode = oldChildren[oldStartIdx];let oldEndVNode = oldChildren[oldEndIdx];let newStartVNode = newChildren[newStartIdx];let newEndVNode = newChildren[newEndIdx];
}
上面的代码中,我们将两组子节点的打补丁工程封装到了 patchKeyedChildren 函数中。该函数中,先获取两组新旧子节点 oldChildren 和 newChildren,然后创建四个索引值,分别指向新旧两组子节点的收尾,即 oldStartIdx(简称为旧前)、oldEndIdx(简称为旧后)、newStartIdx(简称为新前)、newEndIdx(简称为新后),以及四个索引值对应的 vnode。其中 oldStartVNode 和 oldEndVNode 是旧的一组子节点的第一个节点和最后一个节点,newStartVNode 和 newEndVNode 则是新的一组子节点的第一个子节点和最后一个子节点。
双端比较,每一轮均分为四个步骤:
- 比较旧的一组子节点的第一个子节点p-1(简称为旧前)于新的一组子节点的第一个子节点p-4(简称为新前),看看他们是否相同。由于两者的 key 值不同,因此不相同,不可复用,于是什么都不做。
- 比较旧的一组子节点的最后一个子节点p-4(简称为旧后)于新的一组子节点的最后一个子节点p-3(简称为新后),看看他们是否相同。由于两者的 key 值不同,因此不相同,不可复用,于是什么都不做。
- 比较旧的一组子节点的第一个子节点p-1(简称为旧前)于新的一组子节点的最后一个子节点p-3(简称为新后),看看他们是否相同。由于两者的 key 值不同,因此不相同,不可复用,于是什么都不做。
- 比较旧的一组子节点的最后一个子节点p-4(简称为旧后)于新的一组子节点的第一个子节点p-4(简称为新前)。由于他们的 key 相同,因此可以进行DOM复用。
四个步骤命中任何一步均说明命中的节点可以进行DOM复用,因此后续只需要进行DOM移动操作完成更新即可。
function patchKeyedChildren(n1, n2, container) {const oldChildren = n1.children;const newChildren = n2.children;// 四个索引值let oldStartIdx = 0;let oldEndIdx = oldChildren.length - 1;let newStartIdx = 0;let newEndIdx = newChildren.length - 1;// 四个索引指向的 vnode 节点let oldStartVNode = oldChildren[oldStartIdx];let oldEndVNode = oldChildren[oldEndIdx];let newStartVNode = newChildren[newStartIdx];let newEndVNode = newChildren[newEndIdx];while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {if (oldStartVNode.key === newStartVNode.key) {// 步骤一:oldStartVNode 和 newStartVNode 比较// 调用 patch 函数在 oldStartIdx 和 newStartIdx 之间打补丁patch(oldStartVNode, newStartVNode, container);// 更新相关索引到下一个位置oldStartVNode = oldChildren[++oldStartIdx];newStartVNode = newEndVNode[++newEndIdx];} else if(oldEndVNode.key === newEndVNode.key) {// 步骤二:oldEndVNode 和 newEndVNode 比较// 节点在新的顺序中仍然处于尾部,不需要移动,但仍需打补丁patch(oldEndVNode, newEndVNode, container);// 更新索引和头尾部节点变量newEndVNode = newChildren[--newEndIdx];oldEndVNode = oldChildren[--oldEndIdx];} else if(oldStartVNode.key === newEndVNode.key) {// 步骤三:oldStartVNode 和 newEndVNode 比较// 调用 patch 函数在 oldStartIdx 和 newEndIdx之间打补丁patch(oldStartVNode, newEndVNode, container);// 将旧的一组子节点的头部节点对应的真是节点 DOM 节点 oldStartVNode.el 移动// 到旧一组子节点的尾部节点对应的真实 DOM 节点后面insert(oldStartVNode.el, container, oldEndVNode.el.nextSibiling);// 更新相关索引到下一个位置oldStartVNode = oldChildren[++oldStartIdx];newEndVNode = newChildren[--newEndIdx];} else if(oldEndVNode.key === newStartVNode.key) {// 步骤四:oldEndVNode 和 newStartVNode 比较// 仍然需要调用 patch 函数进行打补丁patch(oldEndVNode, newStartVNode, container);// 移动 DOM 操作// oldEndVNode.el 移动到 oldStartVNode.el 前面insert(oldEndVNode.el, container, oldStartVNode.el);// 移动 DOM 完成后,更新索引值,并指向下一个位置oldEndVNode = oldChildren[--oldEndIdx];newStartVNode = newChildren[++newStartIdx];}}
}
上述代码:
- 步骤四中找到了具有相同key值的节点,说明原来处于尾部的节点在新的顺序周中应该处于头部。因此我们只需要以头部元素 oldStartVNode.el 作为锚点,将尾部元素 oldEndVNode.el 移动到锚点前面即可,移动前仍然需要调用 patch 函数在新旧虚拟节点之间打补丁。然后还需要更新索引,oldEndIdx 向上移动,newStartIdx 向下移动,同时更新 oldEndVNode 和 newStartVNode。
- 步骤三中找到了具有相同key值的节点,说明原来处于头部的节点在新的顺序中应该处于尾部。因此我们需要以 oldEndVNode.el.nextSibiling(旧一组节点的尾部节点对应的真实 DOM 节点的兄弟节点) 作为锚点,将头部元素 oldStartVNode.el 移动到锚点之前即可,移动前需要调用 patch 函数对新旧虚拟节点进行打补丁,然后更新相关的索引,oldStartIdx 向下移动,newEndIdx 向上移动,同时更新 oldStartVNode 和 newEndVNode。
- 步骤二中找到了具有相同key值的节点,说明原来处于尾部的节点在新的顺序中仍然处于尾部,因此不需要进行移动,调用 patch 函数进行新旧虚拟节点打补丁,然后更新相关索引,newEndIdx 和 oldEndIdx 均向上移动,同时更新 newEndVNode 和 oldEndVNode。
- 步骤一中找到了具有相同key值的节点,说明原来处于头部的节点在新的顺序中仍然处于头部,因此不需要进行移动,调用 patch 函数进行新旧虚拟节点打补丁,然后更新相关索引,oldStartIdx 和 newEndIdx 均向下移动,同时更新 oldStartVNode 和 newStartVNode。
非理想状况的处理方式

在四个步骤的比较过程中,都无法找到可复用的节点,此时我们通过增加额外的处理步骤(盘外招)来处理这种情况:拿新的一组子节点中的头部节点去旧的一组子节点中寻找,如下代码所示:
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {if (oldStartVNode.key === newStartVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldStartVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newStartVNode.key) {// 省略部分代码} else {// 遍历旧的一组节点,试图寻找与 newStartVNode 拥有相同 key 值的节点// idxInOld 就是新的一组子节点的头部节点在旧的一组节点中的索引const idxInOld = oldChildren.findIndex(ele => ele.key === newStartVNode.key);}
}

上图中我们拿新的一组子节点的头部节点p-2去旧的一组子节点中查找,在索引为1的位置找到了可复用的节点。然后将节点p-2对应的真实 DOM 节点移动到当前旧的一组子节点的头部节点p-1所对应的真实 DOM 节点之前。
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {if (oldStartVNode.key === newStartVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldStartVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newStartVNode.key) {// 省略部分代码} else {// 遍历旧的一组节点,试图寻找与 newStartVNode 拥有相同 key 值的节点// idxInOld 就是新的一组子节点的头部节点在旧的一组节点中的索引const idxInOld = oldChildren.findIndex(ele => ele.key === newStartVNode.key);// idxInOld > 0,说明找了可复用的节点,并且需要将其对应的真实 DOM 移动到头部if (idxInOld) {// idxInOld 位置对应的 vnode 就是需要移动的节点const vnodeToMove = oldChildren[idxInOld];// 不要忘记除移动操作之外还应该打补丁patch(vnodeToMove, newStartVNode, container);// 将 vnodeToMove.el 移动到头部节点 oldStartVNode.el 之前,因此将后者作为锚点insert(vnodeToMove.el, container, oldStartVNode.el);// 由于位置 idxInOld 处的节点所对应的真实 DOM 已经移动了别处,因此将其设置为 undefinedoldChildren[idxInOld] = undefined;// 最后更新 newStartIdx 到下一个位置newStartVNode = newChildren[++newStartIdx];}}
}
上面代码中,首先判断 idxInOld是否大于0,条件成立,说明找到了可复用的节点,然后将该节点进行移动。先获取需要移动的节点(oldChildren[idxInOld]),移动前进行打补丁,然后找到锚点(oldStartVNode.el),调用 insert 函数完成节点移动。移动完成后,需要将 oldChildren[idxInOld] 设置为undefined,同时更新 newStartIdx (向下移动)。

然后再进行双端Diff的四个步骤,进行节点移动和更新操作。由于旧的一组子节点中存在 undefined(说明该节点已经被处理过,直接跳过即可)因此我们需要对代码进行补充。
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {// 增加两个判断分支,如果头部节点为undefined,说明该节点被处理过,直接跳到下一个位置if (!oldStartVNode) {oldStartVNode = oldChildren[++oldStartIdx];} else if (!oldEndVNode) {oldEndVNode = oldChildren[--endStartIdx];} else if (oldStartVNode.key === newStartVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldStartVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newStartVNode.key) {// 省略部分代码} else {// 遍历旧的一组节点,试图寻找与 newStartVNode 拥有相同 key 值的节点// idxInOld 就是新的一组子节点的头部节点在旧的一组节点中的索引const idxInOld = oldChildren.findIndex(ele => ele.key === newStartVNode.key);// idxInOld > 0,说明找了可复用的节点,并且需要将其对应的真实 DOM 移动到头部if (idxInOld) {// idxInOld 位置对应的 vnode 就是需要移动的节点const vnodeToMove = oldChildren[idxInOld];// 不要忘记除移动操作之外还应该打补丁patch(vnodeToMove, newStartVNode, container);// 将 vnodeToMove.el 移动到头部节点 oldStartVNode.el 之前,因此将后者作为锚点insert(vnodeToMove.el, container, oldStartVNode.el);// 由于位置 idxInOld 处的节点所对应的真实 DOM 已经移动了别处,因此将其设置为 undefinedoldChildren[idxInOld] = undefined;// 最后更新 newStartIdx 到下一个位置newStartVNode = newChildren[++newStartIdx];}}
}
添加新元素
前面说了非理想情况的处理,即在一轮比较过程中,不会命中四个步骤中的任何一步。这时我们会拿新的一组子节点中的头部节点去旧的一组子节点中寻找可复用的节点,然而并非总能找到。如下所示:

我们发现经过四个步骤,均没有命中且p-4节点在旧的一组也没有相同的 key 值对应的节点,因此可得p-4节点是一个新增节点,我们应该将该节点挂载到正确的位置上。因为p-4节点是新的一组子节点中的头部节点,所以需要将它挂载到当前头部节点(旧的一组子节点的头部节点p-1)的前面即可。
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {// 增加两个判断分支,如果头部节点为undefined,说明该节点被处理过,直接跳到下一个位置if (!oldStartVNode) {oldStartVNode = oldChildren[++oldStartIdx];} else if (!oldEndVNode) {oldEndVNode = oldChildren[--endStartIdx];} else if (oldStartVNode.key === newStartVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldStartVNode.key === newEndVNode.key) {// 省略部分代码} else if(oldEndVNode.key === newStartVNode.key) {// 省略部分代码} else {// 遍历旧的一组节点,试图寻找与 newStartVNode 拥有相同 key 值的节点// idxInOld 就是新的一组子节点的头部节点在旧的一组节点中的索引const idxInOld = oldChildren.findIndex(ele => ele.key === newStartVNode.key);// idxInOld > 0,说明找了可复用的节点,并且需要将其对应的真实 DOM 移动到头部if (idxInOld) {// idxInOld 位置对应的 vnode 就是需要移动的节点const vnodeToMove = oldChildren[idxInOld];// 不要忘记除移动操作之外还应该打补丁patch(vnodeToMove, newStartVNode, container);// 将 vnodeToMove.el 移动到头部节点 oldStartVNode.el 之前,因此将后者作为锚点insert(vnodeToMove.el, container, oldStartVNode.el);// 由于位置 idxInOld 处的节点所对应的真实 DOM 已经移动了别处,因此将其设置为 undefinedoldChildren[idxInOld] = undefined;// 最后更新 newStartIdx 到下一个位置newStartVNode = newChildren[++newStartIdx];} else {// 将 newStartVNode 作为新的节点挂载到头部,使用当前头部节点 oldStartVNode.el 作为锚点patch(null, newStartVNode, container, oldStartVNode.el);}newStartVNode = newChildren[++newStartIdx];}
}
上面的代码所示,当条件 idxInOld > 0 不成立时,说明 newStartVNode 节点是全新的节点。又由于
newStartVNode 节点是头部节点,因此我们应该将其作为新的头部节点进行挂载。因此我们在调用 patch 函数挂载节点时,我们使用 oldStartVNode.el 作为锚点。这步操作完成之后,新旧两组子节点以及真实 DOM 节点如下图所示。

除了上述新增节点的方式,还有另外一种情况,如下所示:

在经历三轮更新之后,新旧两组子节点以及真实 DOM 节点的状态如下图所示:

可以发现,由于变量 oldStartIdx 的值大于 oldEndIdx 的值,满足更新停止的条件,因此更新停止。但是观察发现,节点p-4在整个更新过程中被遗漏了,因此我们添加额外的代码,代码如下:
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {// 省略部分代码
}
// 循环结束后检查索引值的情况
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {// 如果满足条件,则说明有新的节点遗留,需要挂载他们for (let i = newStartIdx; i <= newEndIdx; i++) {const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null;patch(null, newChildren[i], container, anchor);}
}
我们在while循环之后,增加了一个if条件语句,检查四个索引值的情况。如果满足oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx条件,说明有新的一组子节点中有遗留的节点需要作为新节点挂载。其中索引值位于 newStartIdx 和 newEndIdx 之间的节点都是新节点。于是我们开启一个for循环遍历这个区间的节点,并逐一进行挂载。挂载时的锚点仍然使用当前的头部节点 oldStartVNode.el。
移除不存在的元素
解决了新增节点的问题后,我们来讨论关于移除元素的情况,如下所示:

经过两轮更新后,如下所示:

我们可以发现:此时变量 newStartIdx 的值大于变量 newEndIdx 的值,满足更新停止的条件,于是更新结束。但是旧的一组子节点中存在未被处理的节点,应该将其移除,我们新增额外的代码处理,代码如下:
while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {// 省略部分代码
}
if (oldEndIdx < oldStartIdx && newStart <= newEndIdx) {// 添加新节点// 省略部分代码
} else if (oldEndIdx >= oldStartIdx && newStart > newEndIdx) {// 移除操作for (let i = oldStartIdx; i <= oldEndIdx; i++) {unmount(oldChildren[i]);}
}
与处理新增节点类似,我们在while循环结束后又增加了一个 else…if 分支,用于卸载已经不存在的节点。索引值位于 oldStartIdx 和 oldEndIdx 区间的节点都应该被卸载,于是我们开启一个 for 循环将他们逐一卸载。
完整的代码如下:
function patchKeyedChildren(n1, n2, container) {const oldChildren = n1.children;const newChildren = n2.children;// 四个索引值let oldStartIdx = 0;let oldEndIdx = oldChildren.length - 1;let newStartIdx = 0;let newEndIdx = newChildren.length - 1;// 四个索引指向的 vnode 节点let oldStartVNode = oldChildren[oldStartIdx];let oldEndVNode = oldChildren[oldEndIdx];let newStartVNode = newChildren[newStartIdx];let newEndVNode = newChildren[newEndIdx];while(oldEndIdx >= oldStartIdx && newEndIdx >= newStartIdx) {// 增加两个判断分支,如果头部节点为undefined,说明该节点被处理过,直接跳到下一个位置if (!oldStartVNode) {oldStartVNode = oldChildren[++oldStartIdx];} else if (!oldEndVNode) {oldEndVNode = oldChildren[--endStartIdx];} else if (oldStartVNode.key === newStartVNode.key) {// 第一步:oldStartVNode 和 newStartVNode 比较// 调用 patch 函数在 oldStartIdx 和 newStartIdx 之间打补丁patch(oldStartVNode, newStartVNode, container);// 更新相关索引到下一个位置oldStartVNode = oldChildren[++oldStartIdx];newStartVNode = newEndVNode[++newEndIdx];} else if(oldEndVNode.key === newEndVNode.key) {// 第二步:oldEndVNode 和 newEndVNode 比较// 节点在新的顺序中仍然处于尾部,不需要移动,但仍需打补丁patch(oldEndVNode, newEndVNode, container);// 更新索引和头尾部节点变量newEndVNode = newChildren[--newEndIdx];oldEndVNode = oldChildren[--oldEndVNode];} else if(oldStartVNode.key === newEndVNode.key) {// 第三步:oldStartVNode 和 newEndVNode 比较// 调用 patch 函数在 oldStartIdx 和 newEndIdx之间打补丁patch(oldStartVNode, newEndVNode, container);// 将旧的一组子节点的头部节点对应的真是节点 DOM 节点 oldStartVNode.el 移动// 到旧一组子节点的尾部节点对应的真实 DOM 节点后面insert(oldStartVNode.el, container, oldEndVNode.el.nextSibiling);// 更新相关索引到下一个位置oldStartVNode = oldChildren[++oldStartIdx];newEndVNode = newChildren[--newEndIdx];} else if(oldEndVNode.key === newStartVNode.key) {// 第四步:oldEndVNode 和 newStartVNode 比较// 仍然需要调用 patch 函数进行打补丁patch(oldEndVNode, newStartVNode, container);// 移动 DOM 操作// oldEndVNode.el 移动到 oldStartVNode.el 前面insert(oldEndVNode.el, container, oldStartVNode.el);// 移动 DOM 完成后,更新索引值,并指向下一个位置oldEndVNode = oldChildren[--oldEndIdx];newStartVNode = newChildren[++newStartIdx];} else {// 遍历旧的一组节点,试图寻找与 newStartVNode 拥有相同 key 值的节点// idxInOld 就是新的一组子节点的头部节点在旧的一组节点中的索引const idxInOld = oldChildren.findIndex(ele => ele.key === newStartVNode.key);// idxInOld > 0,说明找了可复用的节点,并且需要将其对应的真实 DOM 移动到头部if (idxInOld) {// idxInOld 位置对应的 vnode 就是需要移动的节点const vnodeToMove = oldChildren[idxInOld];// 不要忘记除移动操作之外还应该打补丁patch(vnodeToMove, newStartVNode, container);// 将 vnodeToMove.el 移动到头部节点 oldStartVNode.el 之前,因此将后者作为锚点insert(vnodeToMove.el, container, oldStartVNode.el);// 由于位置 idxInOld 处的节点所对应的真实 DOM 已经移动了别处,因此将其设置为 undefinedoldChildren[idxInOld] = undefined;// 最后更新 newStartIdx 到下一个位置newStartVNode = newChildren[++newStartIdx];} else {// 将 newStartVNode 作为新的节点挂载到头部,使用当前头部节点 oldStartVNode.el 作为锚点patch(null, newStartVNode, container, oldStartVNode.el);}newStartVNode = newChildren[++newStartIdx];}// 循环结束后检查索引值的情况if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {// 如果满足条件,则说明有新的节点遗留,需要挂载他们for (let i = newStartIdx; i <= newEndIdx; i++) {const anchor = newChildren[newEndIdx + 1] ? newChildren[newEndIdx + 1].el : null;patch(null, newChildren[i], container, anchor);}}
}
相关文章:

双端Diff算法
双端Diff算法 双端Diff算法指的是,在新旧两组子节点的四个端点之间分别进行比较,并试图找到可复用的节点。相比简单Diff算法,双端Diff算法的优势在于,对于同样的更新场景,执行的DOM移动操作次数更少。 简单 Diff 算法…...

react+antd,Table表头文字颜色设置
1、创建一个自定义的TableHeaderCell组件,并设置其样式为红色 const CustomTableHeaderCell ({ children }) > (<th style{{ color: "red" }}>{children}</th> ); 2、将CustomTableHeaderCell组件传递到Table组件的columns属性中的titl…...

2024年1月18日Arxiv最热NLP大模型论文:Large Language Models Are Neurosymbolic Reasoners
大语言模型化身符号逻辑大师,AAAI 2024见证文本游戏新纪元 引言:文本游戏中的符号推理挑战 在人工智能的众多应用场景中,符号推理能力的重要性不言而喻。符号推理涉及对符号和逻辑规则的理解与应用,这对于处理现实世界中的符号性…...

服务限流实现方案
服务限流怎么做 限流算法 计数器 每个单位时间能通过的请求数固定,超过阈值直接拒绝。 通过维护一个单位时间内的计数器,每次请求计数器加1,当单位时间内计数器累加到大于设定的阈值,则之后的请求都被绝,直到单位时…...
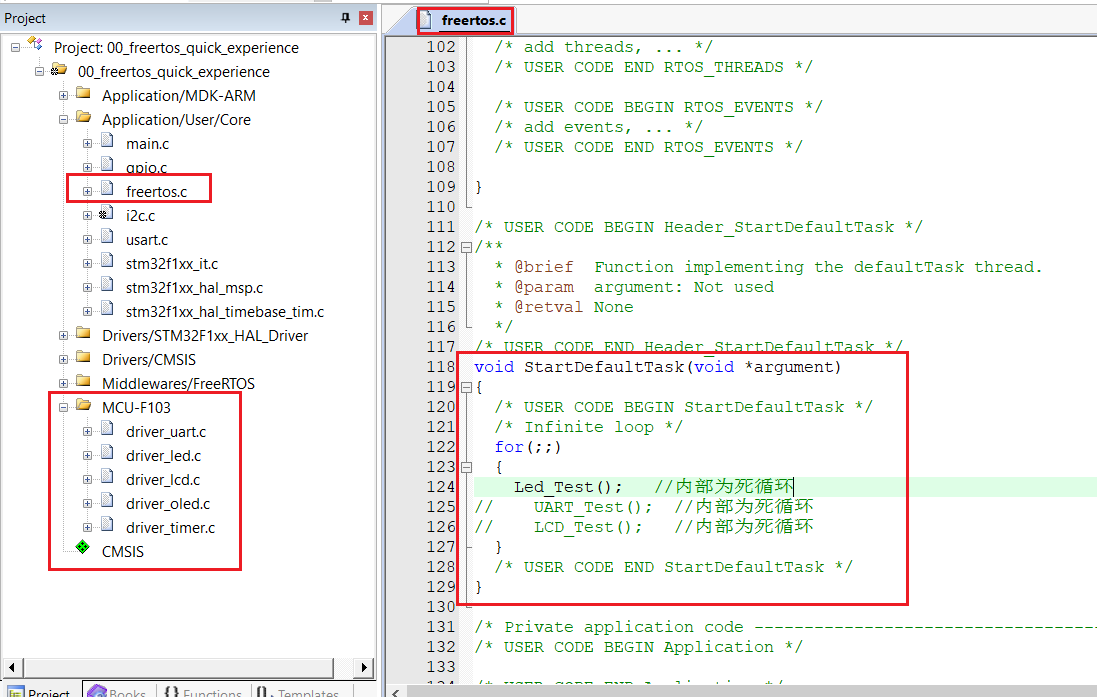
【RTOS】快速体验FreeRTOS所有常用API(1)工程创建
目录 一、工程创建1.1 新建工程1.2 配置RCC1.3 配置SYS1.4 配置外设1)配置 LED PC132)配置 串口 UART13)配置 OLED I2C1 1.5 配置FreeRTOS1.6 工程设置1.7 生成代码1.8 keil设置下载&复位1.9 添加用户代码 快速体验FreeRTOS所有常用API&a…...
Red Hat Enterprise Linux 8.9 安装图解
风险告知 本人及本篇博文不为任何人及任何行为的任何风险承担责任,图解仅供参考,请悉知!本次安装图解是在一个全新的演示环境下进行的,演示环境中没有任何有价值的数据,但这并不代表摆在你面前的环境也是如此。生产环境…...
vcruntime140.dll文件修复的几种常见解决办法,vcruntime140.dll丢失的原因
vcruntime140.dll文件是Windows操作系统中的一个重要动态链接库(DLL)文件,它是Microsoft Visual C Redistributable的一部分。当出现vcruntime140.dll文件丢失的情况时,可能会导致一些程序无法正常运行或出现错误提示。为了电脑能…...

SpringCloud Alibaba 深入源码 - Nacos 分级存储模型、支撑百万服务注册压力、解决并发读写问题(CopyOnWrite)
目录 一、SpringCloudAlibaba 源码分析 1.1、SpringCloud & SpringCloudAlibaba 常用组件 1.2、Nacos的服务注册表结构是怎样的? 1.2.1、Nacos的分级存储模型(理论层) 1.2.2、Nacos 源码启动(准备工作) 1.2.…...
算法训练营Day45
#Java #动态规划 Feeling and experiences: 最长公共子序列:力扣题目链接 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新…...
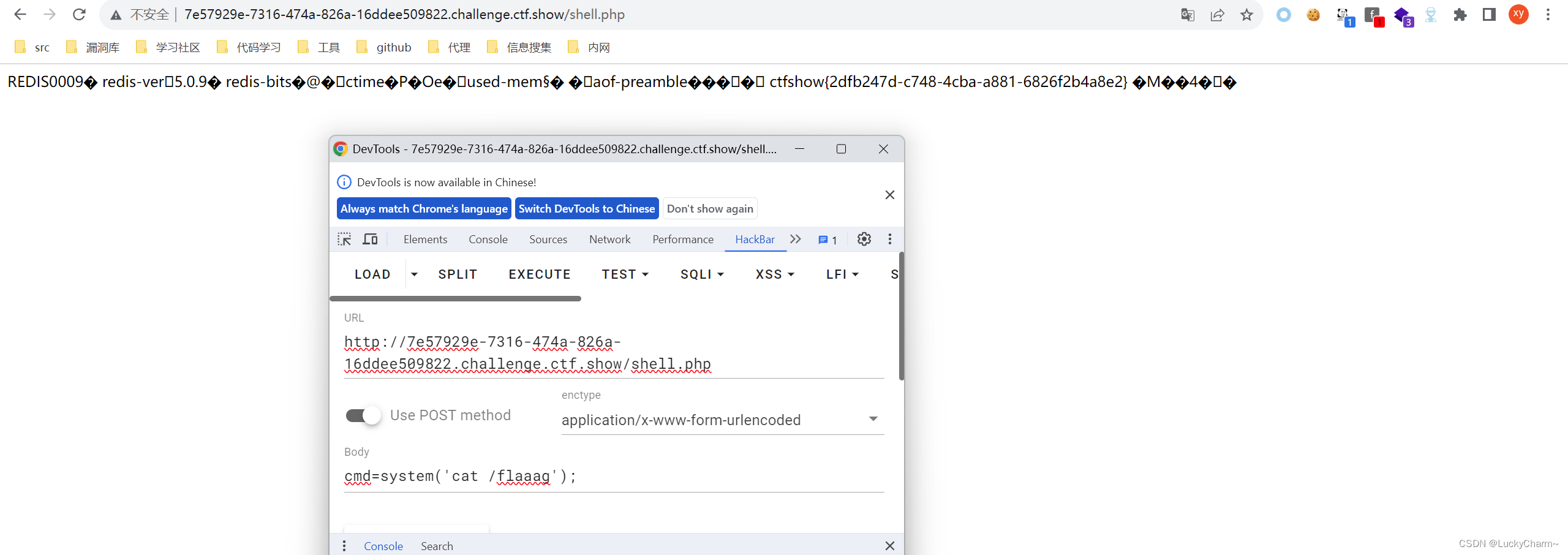
【Redis漏洞利用总结】
前言 redis是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。Redis默认使用 6379 端口。 一、redis未授权访问漏洞 0x01 漏洞描述 描述: Redis是一套开源的使用ANSI C编写、支持网络、可基于内存…...
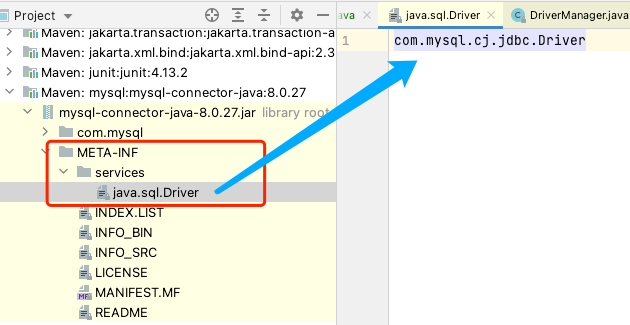
SPI 动态服务发现机制
SPI(Service Provier Interface)是一种服务发现机制,通过ClassPath下的META—INF/services文件查找文件,自动加载文件中定义的类,再调用forName加载; spi可以很灵活的让接口和实现分离, 让API提…...
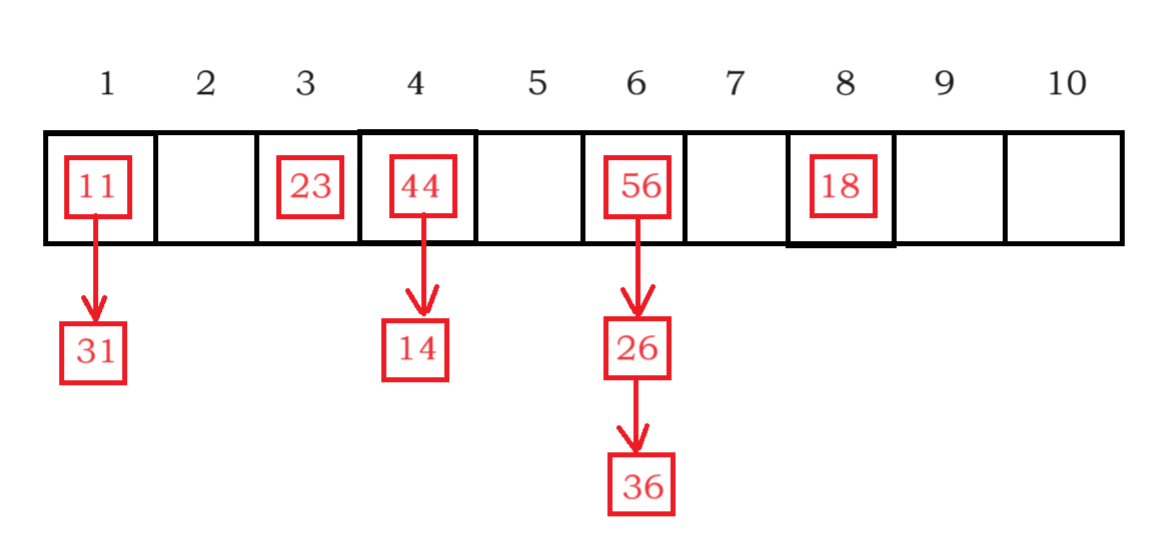
【C++进阶07】哈希表and哈希桶
一、哈希概念 顺序结构以及平衡树中 元素关键码与存储位置没有对应关系 因此查找一个元素 必须经过关键码的多次比较 顺序查找时间复杂度为O(N) 平衡树中为树的高度,即O( l o g 2 N log_2 N log2N) 搜索效率 搜索过程中元素的比较次数 理想的搜索方法:…...

Go 语言实现冒泡排序算法的简单示例
以下是使用 Go 语言实现冒泡排序算法的简单示例: package mainimport "fmt"func bubbleSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {for j : 0; j < n-i-1; j {if arr[j] > arr[j1] {// 交换元素arr[j], arr[j1] arr[j1], arr[j]}}}…...
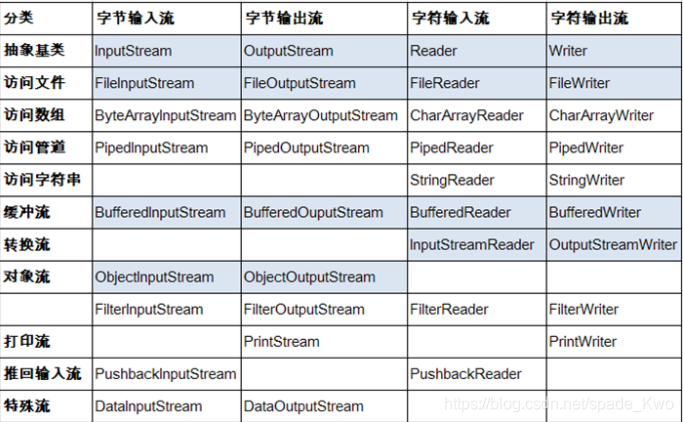
JAVA 学习 面试(五)IO篇
BIO是阻塞I/O,NIO是非阻塞I/O,AIO是异步I/O。BIO每个连接对应一个线程,NIO多个连接共享少量线程,AIO允许应用程序异步地处理多个操作。NIO,通过Selector,只需要一个线程便可以管理多个客户端连接࿰…...
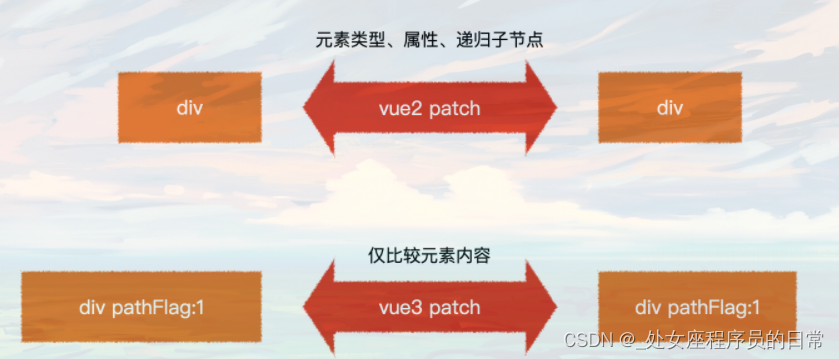
vue3相比vue2的效率提升
1、静态提升 2、预字符串化 3、缓存事件处理函数 4、Block Tree 5、PatchFlag 一、静态提升 在vue3中的app.vue文件如下: 在服务器中,template中的内容会变异成render渲染函数。 最终编译后的文件: 1.静态节点优化 那么这里为什么是两部分…...

web terminal - 如何在mac os上运行gotty
gotty可以让你使用web terminal的方式与环境进行交互,实现终端效果 假设你已经配置好了go环境,首先使用go get github.com/yudai/gotty命令获取可执行文件,默认会安装在$GOPATH/bin这个目录下,注意如果你的go版本比较高ÿ…...
机械设计-哈工大课程学习-螺纹连接
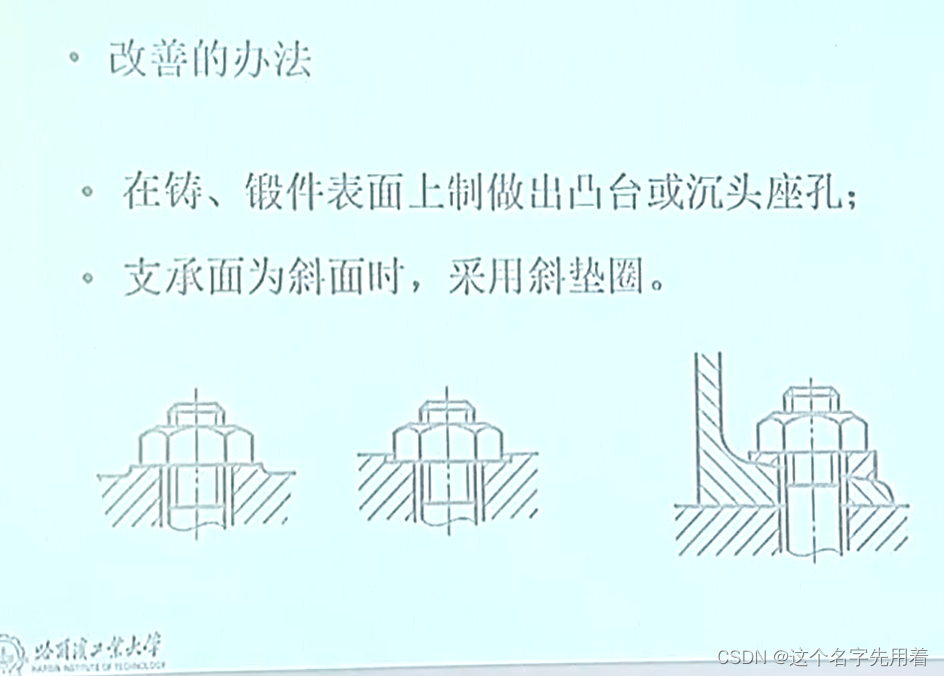
圆柱螺纹主要几何参数螺纹参数 ①外径(大径),与外螺纹牙顶或内螺纹牙底相重合的假想圆柱体直径。螺纹的公称直径即大径。 ②内径(小径),与外螺纹牙底或内螺纹牙顶相重合的假想圆柱体直径。 ③中径ÿ…...

ai绘画|stable diffusion的发展史!简短易懂!!!
手把手教你入门绘图超强的AI绘画,用户只需要输入一段图片的文字描述,即可生成精美的绘画。给大家带来了全新保姆级教程资料包 (文末可获取) 一、stable diffusion的发展史 本文目标:学习交流 对于熟悉SD的同学&#x…...

水塘抽样算法
水塘抽样算法 1、问题描述 最近经常能看到面经中出现在大数据流中的随机抽样问题 即:当内存无法加载全部数据时,如何从包含未知大小的数据流中随机选取k个数据,并且要保证每个数据被抽取到的概率相等。 假设数据流含有N个数,我…...
easyui渲染隐藏域<input type=“hidden“ />为textbox可作为分割条使用
最近在修改前端代码的时候,偶然发现使用javascript代码渲染的方式将<input type"hidden" />渲染为textbox时,会显示一个神奇的效果,这个textbox输入框并不会隐藏,而是显示未一个细条,博主发现非常适合…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
