【数学建模】插值与拟合
文章目录
- 插值
- 插值方法
- 用Python解决插值问题
- 拟合
- 最小二乘拟合
- 数据拟合的Python实现
适用情况
处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式时,构造一个简单函数作为要考察数据或复杂函数的近似
定义
给定一组数据,需要确定满足特定要求的曲线(或曲面)
插值:如果所求曲线通过所给定有限个数据点
拟合:要求所求曲线反映对象整体的变化态势,得到简单实用的近似函数
插值
在一系列数据点对中,一些数据点的函数值缺失,因而希望通过已有数据点得到函数的近似表达式从而近似出确实数据点的函数值
从性质优良、便于计算的函数类{P(x)}中选择一个使得 P ( x i ) = y i P(x_i) =y_i P(xi)=yi成立的P(x)作为f(x)的近似
x 0 , x 1 , . . . , x n x_0, x_1, ..., x_n x0,x1,...,xn成为插值节点
{ P ( x ) } \{P(x)\} {P(x)}称为插值函数类
P ( x i ) = y i ( i = 0 , 1 , . . . , n ) P(x_i) =y_i(i=0, 1, ..., n) P(xi)=yi(i=0,1,...,n)称为插值条件
得到的 P ( x ) P(x) P(x)称为插值函数
f ( x ) f(x) f(x)称为被插值函数
一维插值方法:一维Lagrange插值、分段线性插值、分段二次插值、牛顿插值和样条插值
二维插值方法:二维样条插值
插值方法
Lagrange插值
P ( x ) = ∑ i = 0 n l i ( x ) y i P(x)=\sum^n_{i=0}l_i(x)y_i P(x)=i=0∑nli(x)yi
其中 l i ( x ) l_i(x) li(x)称为以 x 0 , x 1 , . . . , x n x_0, x_1, ..., x_n x0,x1,...,xn为节点的Lagrange插值基函数
l i ( x ) = ∏ j = 0 , j ≠ i n x − x j x i − x j l_i(x) = \prod^n_{j=0, j\neq i} \frac{x-x_j}{x_i-x_j} li(x)=j=0,j=i∏nxi−xjx−xj
代码实现
def h(x,y,a):s = 0.0for i in range(len(y)):t = y[i]for j in range(len(y)):if i != j:t *= (a-x[j])(x[i]-x[j])s += treturn s
分段线性插值
用折线代替曲线 y = f ( x ) y = f(x) y=f(x),其中 P ( x ) P(x) P(x)为
P ( x ) = x − x i x i + 1 − x i y i + 1 + x − x i + 1 x i − x i + 1 y i P(x) = \frac{x-x_i}{x_{i+1}-x_i}y_{i+1} + \frac{x-x_{i+1}}{x_i-x_{i+1}}y_i P(x)=xi+1−xix−xiyi+1+xi−xi+1x−xi+1yi
其中 x ∈ [ x i , x i + 1 ] , i = 0 , 1 , . . . , n − 1 x \in [x_i, x_{i+1}], i=0,1,..., n-1 x∈[xi,xi+1],i=0,1,...,n−1
分段二次插值
P ( x ) P(x) P(x)为一二次多项式,即适用分段抛物线代替 y = f ( x ) y=f(x) y=f(x)
牛顿插值
差分定义:函数 f ( x ) f(x) f(x),等距节点 x i = x 0 + i h ( i = 0 , 1 , . . . , n ) x_i=x_0+ih(i=0, 1, ..., n) xi=x0+ih(i=0,1,...,n),一阶前向差分 Δ f i = f i + 1 − f i \Delta f_i = f_{i+1}-f_i Δfi=fi+1−fi, 高阶差分为差分的差分
- Δ 0 f ( x ) = f ( x ) \Delta^0 f(x) = f(x) Δ0f(x)=f(x)
- Δ m f ( x ) = Δ m − 1 f ( x + h ) − Δ m − 1 f ( x ) \Delta^m f(x) = \Delta^{m-1}f(x+h) - \Delta^{m-1}f(x) Δmf(x)=Δm−1f(x+h)−Δm−1f(x)
递归函数计算差分
def diff_forward(f, k, h, x):if k<=0: return f(x)else: return diff_forward(f, k-1, h, x+h) - diff_forward(f, k-1, h, x)
差商定义:函数 f ( x ) f(x) f(x),相异节点 x 0 < x 1 < . . . < x n x_0 < x_1<... < x_n x0<x1<...<xn
函数 f ( x ) f(x) f(x)关于节点 x i x_i xi, x j x_j xj的一阶差商 f [ x i , x j ] f[x_i, x_j] f[xi,xj]有
f [ x i , x j ] = f ( x i ) − f ( x j ) x i − x j f[x_i, x_j] = \frac{f(x_i)-f(x_j)}{x_i-x_j} f[xi,xj]=xi−xjf(xi)−f(xj)
f ( x ) f(x) f(x)关于点 x i x_i xi, x j x_j xj, x k x_k xk的二阶差商有
f [ x i , x j , x k ] = f [ x i , x j ] − f [ x j , x k ] x i − x k f[x_i, x_j, x_k]= \frac{f[x_i, x_j]-f[x_j, x_k]}{x_i-x_k} f[xi,xj,xk]=xi−xkf[xi,xj]−f[xj,xk]
f ( x ) f(x) f(x)关于 x 0 , x 1 , . . . , x k x_0, x_1, ..., x_k x0,x1,...,xk的 k k k阶差商为
f [ x 0 , x 1 , . . . , x k ] = f [ x 0 , x 1 , . . . , x k − 1 ] − f [ x 1 , x 2 , . . . , x k ] x 0 − x k f[x_0, x_1, ..., x_k] = \frac{f[x_0, x_1, ..., x_{k-1}]-f[x_1, x_2, ..., x_k]}{x_0-x_k} f[x0,x1,...,xk]=x0−xkf[x0,x1,...,xk−1]−f[x1,x2,...,xk]
代码示例:计算 k + 1 k+1 k+1个点对数据的 k k k阶差商
def diff_quo(xi=[], fi=[]):if len(xi)>2 and len(fi)>2:return (diff_quo(xi[:len(xi)-1],fi[:len(fi)-1])-diff_quo(xi[1:len(xi)],fi[1:len(fi)])) / float(xi[0]-xi[-1]) return (fi[0]- fi[1])/float(xi[0]-xi[1])
Newton插值公式
一次Newton插值多项式: N 1 ( x ) = f ( x 0 ) + ( x − x 0 ) f [ x 0 , x 1 ] N_1(x)=f(x_0)+(x-x_0)f[x_0, x_1] N1(x)=f(x0)+(x−x0)f[x0,x1]
再根据各阶差商的定义,可以得到 N n ( x ) N_n(x) Nn(x)即 f ( x ) f(x) f(x)的 n n n次插值多项式
样条插值
适用于对插值函数的光滑性有较高要求的问题
样条函数:具有一定光滑性的分段多项式
给定 [ a , b ] [a,b] [a,b]的一个分划, Δ : a = x 0 < x 1 < . . . < x n = b \Delta: a=x_0 < x_1 < ... < x_n=b Δ:a=x0<x1<...<xn=b
若 S ( x ) S(x) S(x)在各个小区间 [ x i , x i + 1 ] ( i = 0 , 1 , . . . , n − 1 ) [x_i, x_{i+1}](i=0, 1, ..., n-1) [xi,xi+1](i=0,1,...,n−1)上为 m m m次多项式,且有 m − 1 m-1 m−1阶连续导数,称 S ( x ) S(x) S(x)为关于分划 Δ \Delta Δ的 m m m次样条函数,折线属于一次样条曲线
二维数据的双三次样条插值
考虑二维数据的插值时,需要考虑到插值区域是否规则,给定数据是有规律分布的还是散乱、随机分布的
当二维数据在规则区域上有规律分布时,可以考虑用双三次样条插值,即求解一个 S ( x ) S(x) S(x)满足对 x x x和 y y y都是三次的多项式
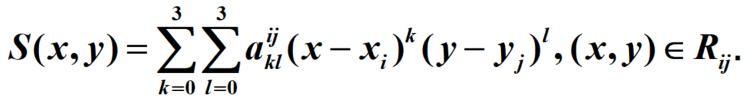
用Python解决插值问题
scipy.interpolatemodule有一维插值函数interp1d、二维插值函数interp2d和多维插值函数interpn
一维插值
interp1d(x, y, kind='linear')
说明:kind参数取值为字符串,指明插值方法,取值包括linear线性插值、zero0阶样条插值、slinear1阶样条插值、quadratic2阶样条插值、cubic3阶样条插值

代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x=np.arange(0,25,2)
y=np.array([12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13])
xnew=np.linspace(0, 24, 500) #插值点
f1=interp1d(x, y);
y1=f1(xnew);
f2=interp1d(x, y,'cubic');
y2=f2(xnew)
plt.rc('font',size=16);
plt.rc('font',family='SimHei')
plt.subplot(121)
plt.plot(xnew, y1)
plt.xlabel("(A)分段线性插值")
plt.subplot(122)
plt.plot(xnew, y2)
plt.xlabel("(B)三次样条插值")
plt.savefig("figure7_4.png", dpi=500)
plt.show()
二维网格节点插值

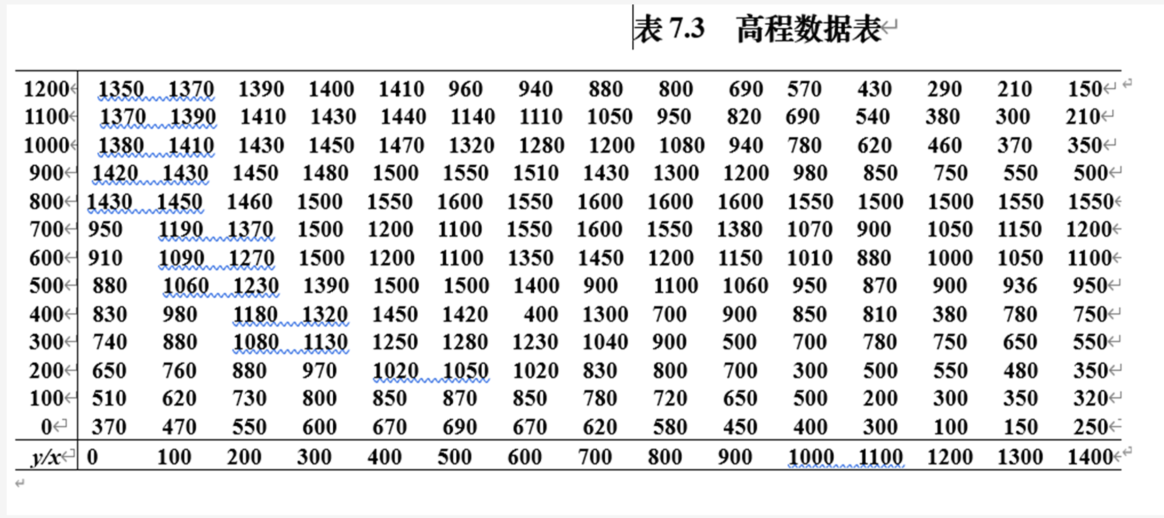
思路:原始数据为100x100网格节点的数据,为提高精度,适用双三次样条插值,得到该区域上10x10网格节点的数据。把 0 ≤ x ≤ 1400 ∧ 0 ≤ y ≤ 1200 0 \leq x \leq 1400 \land 0 \leq y \leq 1200 0≤x≤1400∧0≤y≤1200 数据分为140x120个小矩形计算对应曲面面积,每个矩形分为两个三角形,再利用海伦公式求解
代码:
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import norm
from scipy.interpolate import interp2d
z=np.loadtxt("Pdata7_5.txt") #加载高程数据
x=np.arange(0,1500,100)
y=np.arange(1200,-100,-100)
f=interp2d(x, y, z, 'cubic')
xn=np.linspace(0,1400,141)
yn=np.linspace(0,1200,121)
zn=f(xn, yn)
m=len(xn); n=len(yn); s=0;
for i in np.arange(m-1):for j in np.arange(n-1):p1=np.array([xn[i],yn[j],zn[j,i]])p2=np.array([xn[i+1],yn[j],zn[j,i+1]])p3=np.array([xn[i+1],yn[j+1],zn[j+1,i+1]])p4=np.array([xn[i],yn[j+1],zn[j+1,i]])p12=norm(p1-p2); p23=norm(p3-p2); p13=norm(p3-p1);p14=norm(p4-p1); p34=norm(p4-p3);L1=(p12+p23+p13)/2;s1=np.sqrt(L1*(L1-p12)*(L1-p23)*(L1-p13));L2=(p13+p14+p34)/2; s2=np.sqrt(L2*(L2-p13)*(L2-p14)*(L2-p34));s=s+s1+s2;
print("区域的面积为:", s)
plt.rc('font',size=16); plt.rc('text',usetex=True)
plt.subplot(121); contr=plt.contour(xn,yn,zn); plt.clabel(contr)
plt.xlabel('$x$'); plt.ylabel('$y$',rotation=90)
ax=plt.subplot(122,projection='3d');
X,Y=np.meshgrid(xn,yn)
ax.plot_surface(X, Y, zn,cmap='viridis')
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.savefig('figure7_5.png',dpi=500); plt.show()
二维乱点插值
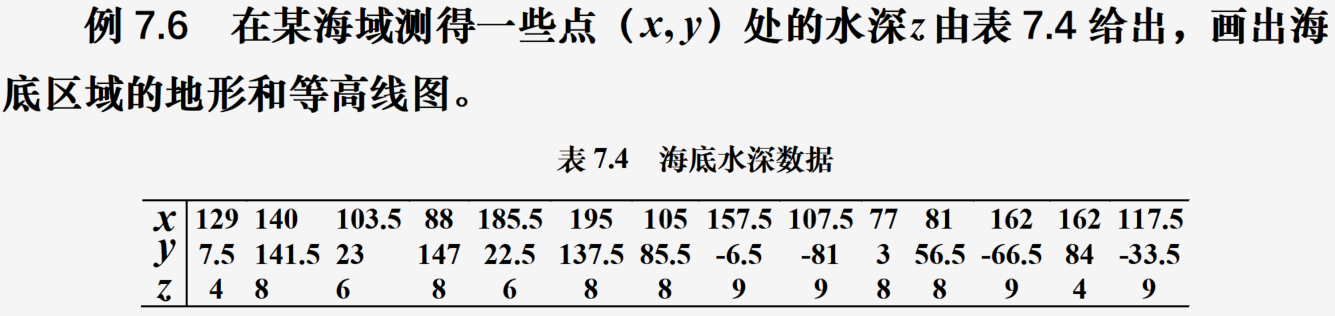
代码:
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata
x=np.array([129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5])
y=np.array([7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5])
z=-np.array([4,8,6,8,6,8,8,9,9,8,8,9,4,9])
xy=np.vstack([x,y]).T
xn=np.linspace(x.min(), x.max(), 100)
yn=np.linspace(y.min(), y.max(), 100)
xng, yng = np.meshgrid(xn,yn) #构造网格节点
zn=griddata(xy, z, (xng, yng), method='nearest') #最近邻点插值
plt.rc('font',size=16); plt.rc('text',usetex=True)
ax=plt.subplot(121,projection='3d');
ax.plot_surface(xng, yng, zn,cmap='viridis')
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.subplot(122); c=plt.contour(xn,yn,zn,8); plt.clabel(c)
plt.savefig('figure7_6.png',dpi=500); plt.show()
拟合
最小二乘拟合
解决什么问题?
已知一组二维数据,即平面上 n n n个点 ( x i , y i ) ( i = 1 , 2 , . . . , n ) (x_i, y_i)(i=1, 2, ..., n) (xi,yi)(i=1,2,...,n), x i x_i xi互不相同,求函数 f ( x ) f(x) f(x)使得 f ( x ) f(x) f(x)在某种准则下与所有数据点最为接近,即曲线拟合得最好
残差: δ i = f ( x i ) − y i , i = 1 , 2 , . . . , n \delta_i=f(x_i)-y_i, i=1,2,...,n δi=f(xi)−yi,i=1,2,...,n
最小二乘法使用的判定准则为残差的平和和最小,即
a r g m i n J = ∑ i = 1 n ( f ( x i ) − y i ) 2 argmin \quad J=\sum^n_{i=1}(f(x_i)-y_i)^2 argminJ=i=1∑n(f(xi)−yi)2
最终得到拟合函数 f ( x ) = f ( x , a 1 , a 2 , . . . , a n ) f(x) = f(x, a_1, a_2, ..., a_n) f(x)=f(x,a1,a2,...,an)
根据参数 a 1 , a 2 , . . . , a n a_1, a_2, ..., a_n a1,a2,...,an线性与否,最小二乘法分为线性最小二乘和非线性最小二乘
线性最小二乘法
给定线性无关的函数系 { ϕ k ( x ) ∣ k = 1 , 2 , . . . , m } \{\phi_k(x)|k=1,2,...,m\} {ϕk(x)∣k=1,2,...,m}
若有拟合函数 f ( x ) = ∑ k = 1 m a k ϕ k ( x ) f(x) = \sum^m_{k=1}a_k \phi_k(x) f(x)=∑k=1makϕk(x),例如 f ( x ) = a m x m − 1 + a m − 1 x m − 2 + . . . + a 2 x + a 1 f(x)=a_mx^{m-1}+a_{m-1}x^{m-2}+...+a_2x+a_1 f(x)=amxm−1+am−1xm−2+...+a2x+a1 或 f ( x ) = ∑ k = 1 m a k c o s ( k x ) f(x) = \sum^m_{k=1}a_k cos(kx) f(x)=∑k=1makcos(kx)
称 f ( x ) = f ( x , a 1 , a 2 , . . . , a m ) f(x)=f(x,a_1, a_2, ..., a_m) f(x)=f(x,a1,a2,...,am)为关于参数 a 1 , a 2 , . . . , a m a_1,a_2,..., a_m a1,a2,...,am的线性函数
将 f ( x ) f(x) f(x)带入 J J J的计算,根据
∂ J ∂ a k = 0 , k = 1 , 2 , ⋯ , m \frac{\partial J}{\partial a_k}=0,\quad k=1,2,\cdots,m ∂ak∂J=0,k=1,2,⋯,m
即:
∑ i = 1 n [ ( f ( x i ) − y i ) φ k ( x i ) ] = 0 , k = 1 , 2 , ⋯ , m \sum_{i=1}^{n}\left[\left(f\left(x_{i}\right)-y_{i}\right) \varphi_{k}\left(x_{i}\right)\right]=0, \quad k=1,2, \cdots, m i=1∑n[(f(xi)−yi)φk(xi)]=0,k=1,2,⋯,m
得到:
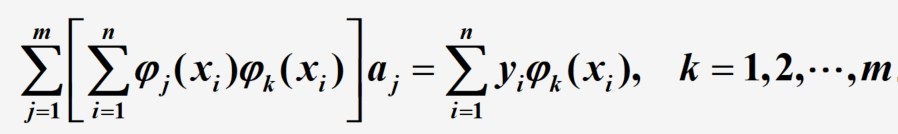
形成一个关于 a 1 , a 2 , . . . , a m a_1,a_2,...,a_m a1,a2,...,am的线性方程组,记号说明如下:
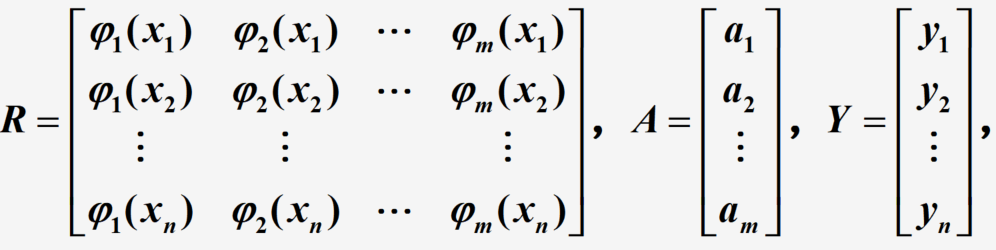
则正规方程组改写为
R T R A = R T Y R^TRA=R^TY RTRA=RTY
当矩阵 R R R列满秩时, R T R R^TR RTR可逆,此时正规方程组有唯一解,即
A = ( R T R ) − 1 R T Y A=(R^TR)^{-1}R^TY A=(RTR)−1RTY
非线性最小二乘拟合
当拟合函数不能以 ϕ k ( x ) \phi_k(x) ϕk(x)线性组合的形式构成时,例如下列形式:
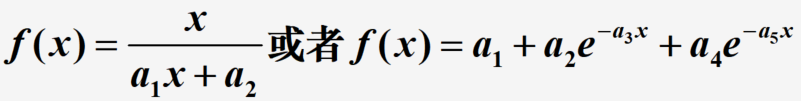
使用同样的“最小化偏差”方法求解参数
拟合函数的选择
先做出数据的散点图,从直观上判断应选用什么样的拟合函数
举个例子
若数据分布接近直线,使用线性函数 f ( x ) = a 1 x + a 2 f(x)=a_1x+a_2 f(x)=a1x+a2
若数据分布接近抛物线,使用二次多项式 f ( x ) = a 1 x 2 + a 2 x + a 3 f(x)=a_1x^2+a_2x+a_3 f(x)=a1x2+a2x+a3
若数据分布是开始上升块随后逐渐变缓,使用双曲线型函数或指数型函数,即
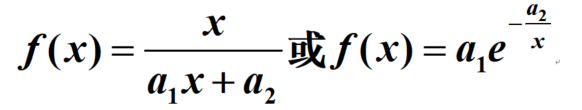
若数据分布是开始下降较快随后逐渐变缓,使用
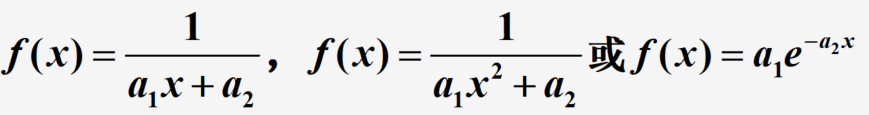
数据拟合的Python实现
利用NumPy库中的多项式拟合函数polyfit或scipy.optimize模块中的curve_fit函数
polyfit的用法
代码展示:
from numpy import polyfit, polyval, array, arange
from matplotlib.pyplot import plot,show,rc
x0=arange(0, 1.1, 0.1)
y0=array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
p=polyfit(x0, y0, 2) #拟合二次多项式
print("拟合二次多项式的从高次幂到低次幂系数分别为:",p)
yhat=polyval(p,[0.25, 0.35]); print("预测值分别为:", yhat)
rc('font',size=16)
plot(x0, y0, '*', x0, polyval(p, x0), '-'); show()
curve_fit的用法
调用格式
popt, pcov = curve_fit(func, xdata, ydata)
参数说明:func为拟合的函数,xdata是自变量的观测值,ydata是函数的观测值,返回值popt是拟合的参数,pcov是参数的协方差矩阵
代码展示:
import numpy as np
from scipy.optimize import curve_fit
y=lambda x, a, b, c: a*x**2+b*x+c
x0=np.arange(0, 1.1, 0.1)
y0=np.array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
popt, pcov=curve_fit(y, x0, y0)
print("拟合的参数值为:", popt)
print("预测值分别为:", y(np.array([0.25, 0.35]), *popt))
实例练习

代码:
import numpy as np
from scipy.optimize import curve_fit
x0=np.array([6, 2, 6, 7, 4, 2, 5, 9])
y0=np.array([4, 9, 5, 3, 8, 5, 8, 2])
z0=np.array([5, 2, 1, 9, 7, 4, 3, 3])
xy0=np.vstack((x0, y0))
def Pfun(t, a, b, c):return a*np.exp(b*t[0])+c*t[1]**2
popt, pcov=curve_fit(Pfun, xy0, z0)
print("a,b,c的拟合值为:", popt)
代码:
from mpl_toolkits import mplot3d
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
m=200; n=300
x=np.linspace(-6, 6, m); y=np.linspace(-8, 8, n);
x2, y2 = np.meshgrid(x, y)
x3=np.reshape(x2,(1,-1)); y3=np.reshape(y2, (1,-1))
xy=np.vstack((x3,y3))
def Pfun(t, m1, m2, s):return np.exp(-((t[0]-m1)**2+(t[1]-m2)**2)/(2*s**2))
z=Pfun(xy, 1, 2, 3); zr=z+0.2*np.random.normal(size=z.shape) #噪声数据
popt, pcov=curve_fit(Pfun, xy, zr) #拟合参数
print("三个参数的拟合值分别为:",popt)
zn=Pfun(xy, *popt) #计算拟合函数的值
zn2=np.reshape(zn, x2.shape)
plt.rc('font',size=16)
ax=plt.axes(projection='3d') #创建一个三维坐标轴对象
ax.plot_surface(x2, y2, zn2,cmap='gist_rainbow')
plt.savefig("figure7_10.png", dpi=500); plt.show()
相关文章:
【数学建模】插值与拟合
文章目录 插值插值方法用Python解决插值问题 拟合最小二乘拟合数据拟合的Python实现 适用情况 处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式时,构造一个简单函数作为要考察数据或复杂函数的近似 定义 给定一组数据,需要确定满…...
全卷积网络:革新图像分析
一、介绍 全卷积网络(FCN)的出现标志着计算机视觉领域的一个重要里程碑,特别是在涉及图像分析的任务中。本文深入探讨了 FCN 的概念、它们的架构、它们与传统卷积神经网络 (CNN) 的区别以及它们在各个领域的应用。 就像…...

ubuntu20.04 格式化 硬盘 扩展硬盘GParted
如何在 Ubuntu 22.04 LTS 上安装分区编辑器 GParted?_gparted安装-CSDN博客 sudo apt install gparted 步骤5:启动GParted 安装完成后,您可以在应用程序菜单中找到GParted。点击它以启动分区编辑器。 通过以上步骤,您可以在Ubun…...

docker的资源限制(cgroup)
前瞻 Docker 通过 Cgroup 来控制容器使用的资源配额,包括 CPU、内存、磁盘三大方面, 基本覆盖了常见的资源配额和使用量控制。 Cgroup 是 ControlGroups 的缩写,是 Linux 内核提供的一种可以限制、记录、隔离进程组所使用的物理资源(如 CPU、…...

ChatGPT与文心一言:应用示例与体验比较
ChatGPT 和文心一言哪个更好用? 为了更好地感受ChatGPT和文心一言这两款AI助手如何在实际运用中竞相辉映,我将提供一些典型的应用示例。这些示例都取自真实的用户体验,以帮助解释这两种工具如何让日常生活或工作变得更加轻松。 ChatGPT Ch…...
紫光展锐T760_芯片性能介绍_展锐T760安卓核心板定制
展锐T760核心板是一款基于国产5G芯片的智能模块,采用紫光展锐T760制程工艺为台积电6nm工艺,支持工艺具有出色的能效表现。其采用主流的44架构的八核设计,包括4颗2.2GHz A76核心和4颗A55核心设计,内存单元板载可达8GB Ram256GB ROM…...

从动力系统研究看当今数学界
6.3... Milnor’s definition of “attractors” which has been criticized above by us). The work of [KSS2] of asserting the existence of “nice open set” of Ω(p.148) would be likely not verified, for example we think the first sentence “… since f is nont…...
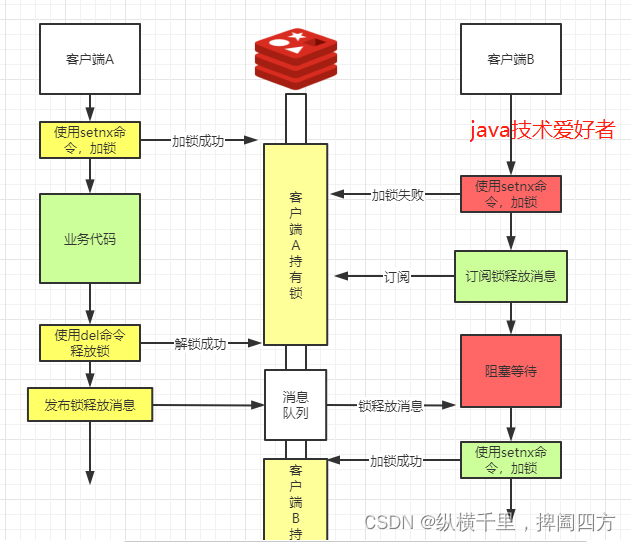
【征服redis15】分布式锁的功能与整体设计方案
目录 1. 分布式锁的概念 2.基于数据库做分布式锁 2.1 基于表主键唯一做分布式锁 2.2 基于表字段版本号做分布式锁 2.3 基于数据库排他锁做分布式锁 3.使用Redis做分布式锁 3.1 redis实现分布式锁的基本原理 3.2 问题一:增加超时机制,防止长期持有…...

MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法
MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法。阻尼最小二乘法通常用于处理数值求解问题中的不稳定性和噪声。以下是一个简单的MATLAB代码示例,演示了机械臂逆运动学的阻尼最小二乘法求解: % 机械臂参数 L1 1; % 机械臂长度 L2 1;…...
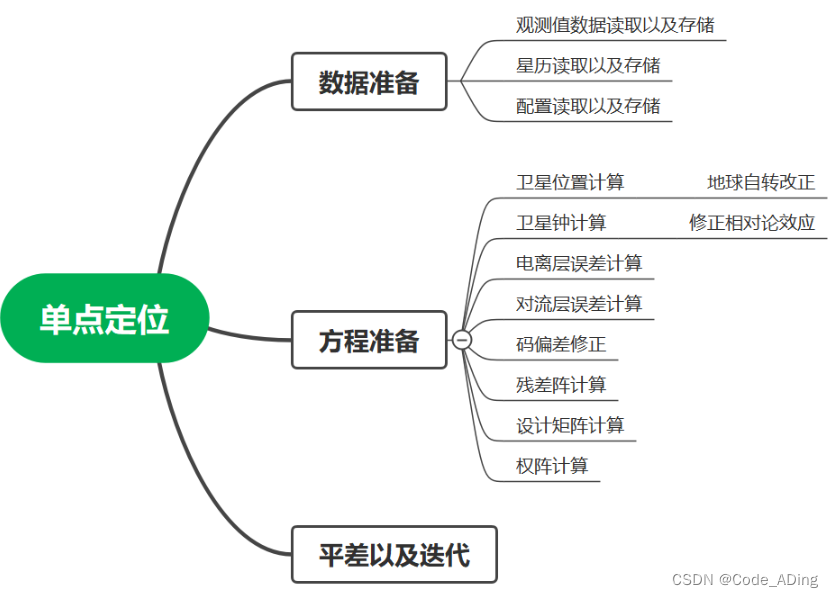
2024.1.24 GNSS 学习笔记
1.伪距观测值公式 2.载波相位观测值公式 3.单点定位技术(Single Point Positionin, SPP) 仅使用伪距观测值,不使用其他的辅助信息获得ECEF框架下绝对定位技术。 使用广播星历的轨钟进行定位,考虑到轨钟的米级精度,所以对于<1米的误差&…...
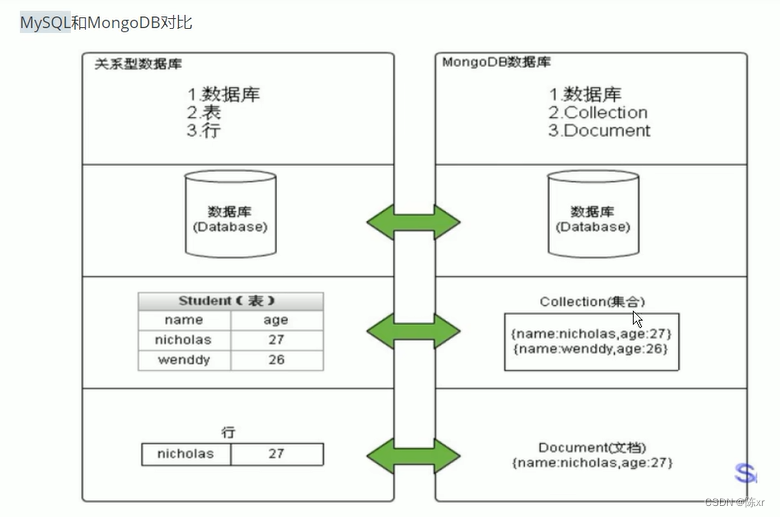
2024-01-22(MongoDB)
1.Mongodb使用的业务场景: 传统的关系型数据库/mysql在“三高”需求以及应对web2.0的网站需求面前,有点力不从心,什么是“三高”需求: a. 对数据库高并发的读写需求 b. 对海量数据的高效率存储和访问需求 c. 对数据库的高可扩…...
无人机航迹规划(六):七种元启发算法(DBO、LO、SWO、COA、LSO、KOA、GRO)求解无人机路径规划(提供MATLAB代码)
一、七种算法(DBO、LO、SWO、COA、LSO、KOA、GRO)简介 1、蜣螂优化算法DBO 蜣螂优化算法(Dung beetle optimizer,DBO)由Jiankai Xue和Bo Shen于2022年提出,该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁…...
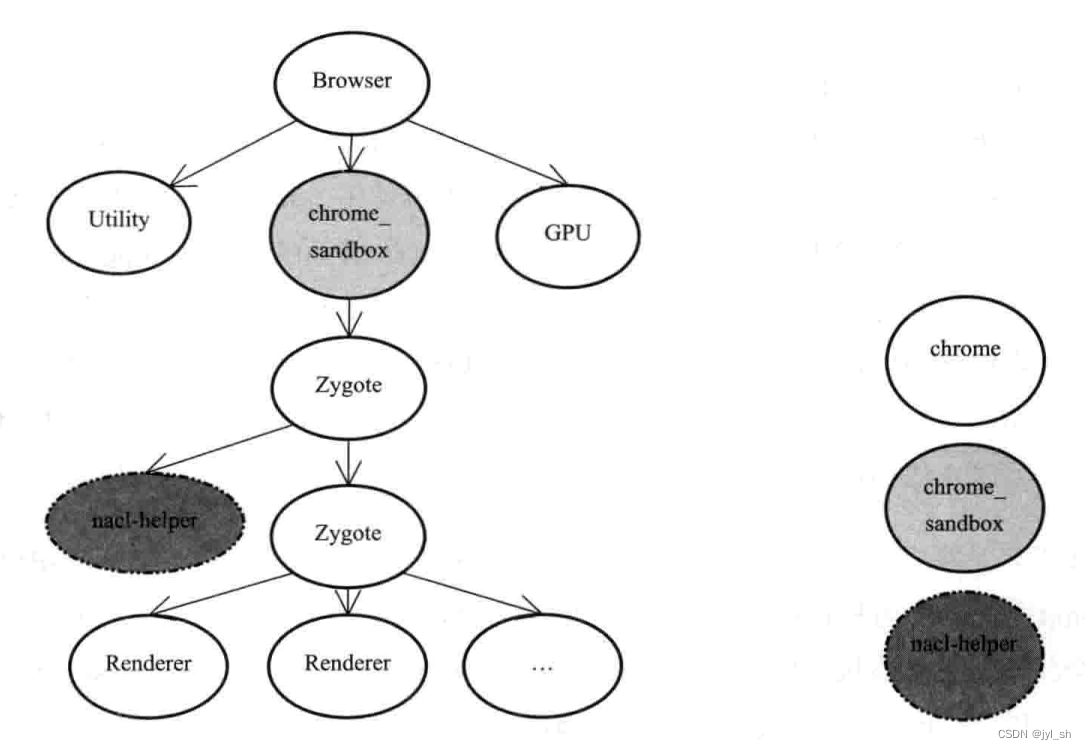
《WebKit 技术内幕》学习之十二(2):安全机制
2 沙箱模型 2.1 原理 一般而言,对于网络上的网页中的JavaScript代码和插件是不受信的(除非是经过认证的网站),特别是一些故意设计侵入浏览器运行的主机代码更是非常危险,通过一些手段或者浏览器中的漏洞,…...
算法优化:LeetCode第122场双周赛解题策略与技巧
接下来会以刷常规题为主 ,周赛的难题想要独立做出来还是有一定难度的,需要消耗大量时间 比赛地址 3011. 判断一个数组是否可以变为有序 public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时&a…...
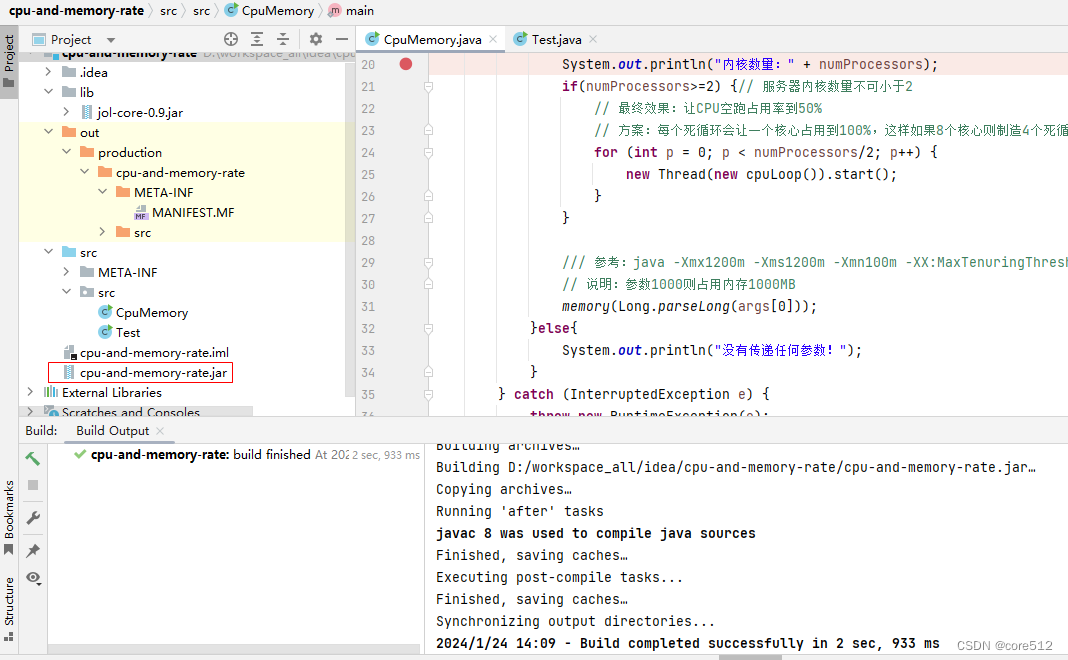
IDEA导出jar
1、选择导出方式 2、选择Main Class 3、构建jar...
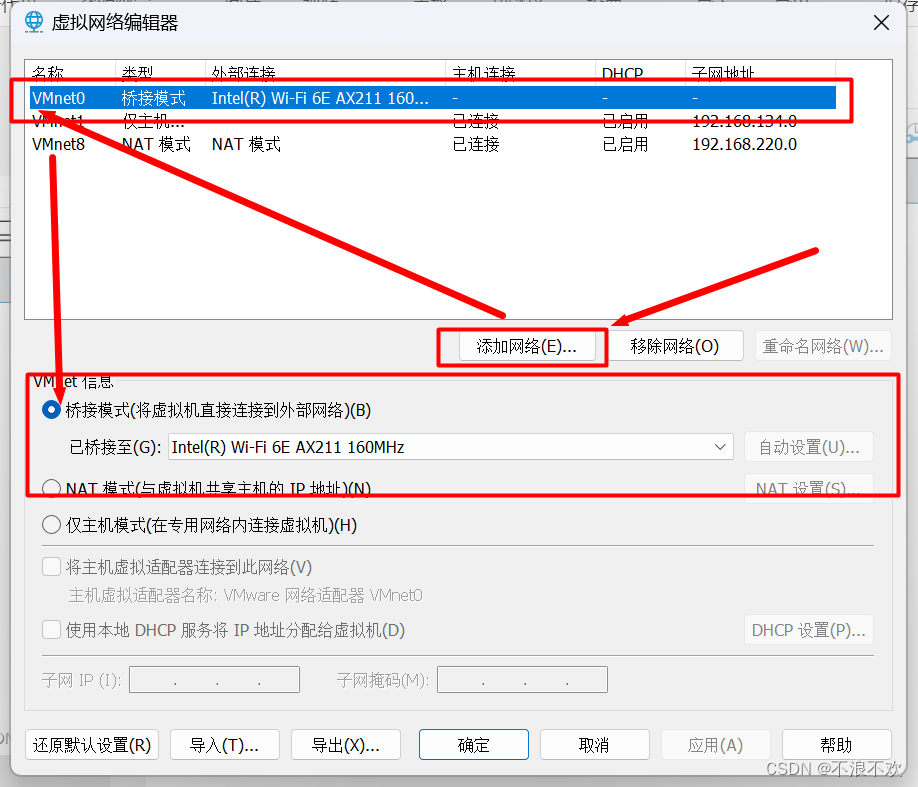
Win10/11中VMware Workstation设置网络桥接模式
文章目录 一、添加VMware Bridge Protocol服务二、配置桥接参数1.启用系统Device Install Service服务2.配置VMware 需要确认物理网卡是否有添加VMware Bridge Protocol服务 添加VMware Bridge Protocol服务 提示:以下是本篇文章正文内容,下面案例可供参…...

html Canvas粒子文字特效
代码有点长,下面是代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>HTML5 Canvas粒子效果文字动画特效DEMO演示</title><link rel"stylesheet" href"css/normalize.c…...

@JsonFormat失效,被jackson自定义配置覆盖
jackson配置类 我的jackson配置类如下,其中serializerByType(LocalDateTime.class, new LocalDateTimeSerializer()) 覆盖了JsonFormat注解 Configuration public class JacksonConfiguration {public static final DateTimeFormatter optionalDateTimePattern (n…...
SaaS系统如何助力企业数字化转型
随着科技的快速发展,数字化转型已经成为企业适应市场变化、提高竞争力的必要手段。在这个过程中,SaaS(软件即服务)系统以其独特的优势,正在成为越来越多企业的首选。乔拓云SaaS系统作为这一领域的佼佼者,更…...
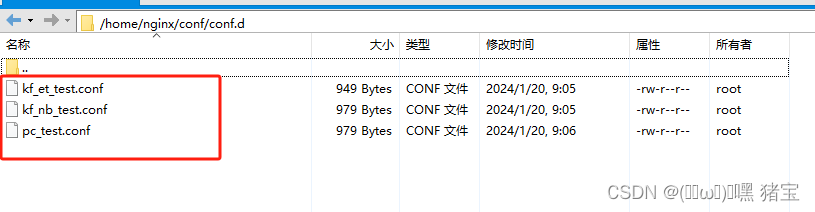
nginx配置内网代理,前端+后端分开配置
安装好后nginx,进入配置文件 我这块安装在了home里面,各位根据自身情况选择 打开nginx.conf文件 在底部查看是否包含这段信息:含义是配置文件包含该路径下的配置文件 include /home/nginx/conf/conf.d/*.conf; # 该路径根据自己的安装位置自行修改 配置文件 进入conf.d文…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
