Objective-C方法的声明实现及调用
1.无参数的方法
1)声明
a.位置:在@interface括弧的外面
b.语法:
- (返回值类型)方法名称;
@interface Person : NSObject
-(void) run;
@end2)实现
a.位置:在@implementation中实现
b.语法:加大括弧将方法实现的代码写在大括孤之中
@implementation Person;
-(void)run{NSLog(@"我在跑步");
}
@end3)调用
a.方法是无法直接调用的,因为类是不能直接使用的,必须要先创建对象
b.语法:
[对象名 方法名];
int main(int argc, const char * argv[]) {Person *p = [Person new];[p run];
}2.单个参数的方法
1)声明
a.位置:在@interface括弧的外面
b.语法:
-(返回值类型)方法名称:(参数类型)形参名称;
@interface Person : NSObject
-(void)eat:(NSString *)foodName;
@end2)实现
a.位置:在@implementation中实现
b.语法:加大括弧将方法实现的代码写在大括孤之中
@implementation Person;
-(void)eat:(NSString *)foodName{NSLog(@"%@好美味!",foodName);
}
@end3)调用
a.方法是无法直接调用的,因为类是不能直接使用的,必须要先创建对象
b.语法:
[对象名 方法名:实参];
int main(int argc, const char * argv[]) {Person *p = [Person new];[p eat:@"烤鱼"];
}3.多个参数的方法
1)声明
a.位置:在@interface括弧的外面
b.语法:
-(返回值类型)方法名称:(参数类型)形参名称 :(参数类型)形参名称;
@interface Person : NSObject
-(int)sum:(int)num1 :(int)num2;
@end2)实现
a.位置:在@implementation中实现
b.语法:加大括弧将方法实现的代码写在大括孤之中
@implementation Person;
-(int)sum:(int)num1 :(int)num2{int num = num1+num2;return num;
}
@end3)调用
a.方法是无法直接调用的,因为类是不能直接使用的,必须要先创建对象
b.语法:
[对象名 方法名:实参:实参];
int main(int argc, const char * argv[]) {Person *p = [Person new];NSLog(@"sum=%d",[p sum:1 :1]);
}运行结果

相关文章:

Objective-C方法的声明实现及调用
1.无参数的方法 1)声明 a.位置:在interface括弧的外面 b.语法: - (返回值类型)方法名称; interface Person : NSObject -(void) run; end 2)实现 a.位置:在implementation中实现 b.语法:加大括弧将方法实现的代码写在大括孤之中 …...
)
第十四届蓝桥杯国赛 C++ B 组 C 题——班级活动(AC)
目录 1. 班级活动1. 问题描述2. 输入格式3. 输出格式4. 样例输入5. 样例输出6. 样例说明7. 评测用例规模与约定8. 原题链接 2. 解题思路3. AC_Code 1. 班级活动 前置知识点:思维,分类讨论 1. 问题描述 小明的老师准备组织一次班级活动。班上一共有 n…...

GraphQL的力量:简化复杂数据查询
1. GraphQL GraphQL 是一种由 Facebook 开发并于 2015 年公开发布的数据查询和操作语言,也是运行在服务端的运行时(runtime)用于处理 API 查询的一种规范。不同于传统的 REST API,GraphQL 允许客户端明确指定它们需要哪些数据&am…...
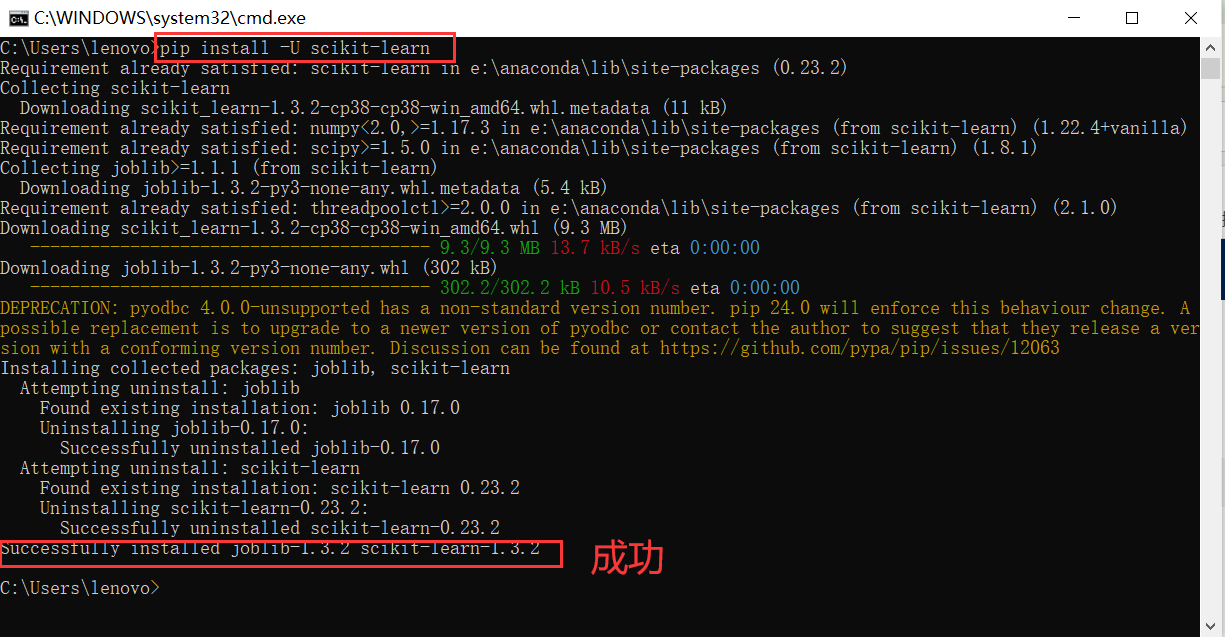
python环境安装sklearn及报错解决
安装 如刚开始安装,还未遇到问题请直接从重新安装库开始看,如果遇到报错,从问题开始看 问题 python安装sklearn报错 ,报错信息如下 File "<stdin>", line 1pip install scikit-learn^ SyntaxError: invalid s…...

log4j:WARN Please initialize the log4j system properly的解决办法
背景:很多次创建新项目log4j都出现以下2个警告: log4j:WARN No appenders could be found for logger (org.springframework.boot.ApplicationServletEnvironment).log4j:WARN Please initialize the log4j system properly 网上查询都是在说缺少以下jar…...

虹科分享丨汽车技术的未来:Netropy如何测试和确保汽车以太网的性能
来源:艾特保IT 虹科分享丨汽车技术的未来:Netropy如何测试和确保汽车以太网的性能 原文链接:https://mp.weixin.qq.com/s/G8wihrzqpJJOx5i0o63fkA 欢迎关注虹科,为您提供最新资讯! #汽车以太网 #车载网络 #Netropy …...

代码CE:reference to ‘XX‘ is ambiguous
代码CE:reference to ‘XX’ is ambiguous 今天提交代码的时候一直错误,CE,搞不明白明明在dev上成功,为什么提交失败。 现在懂了,因为定义的变量和C内部函数或变量重名了。修改之后即可AC。 int data[21][21]{0}; int maxsum[21…...
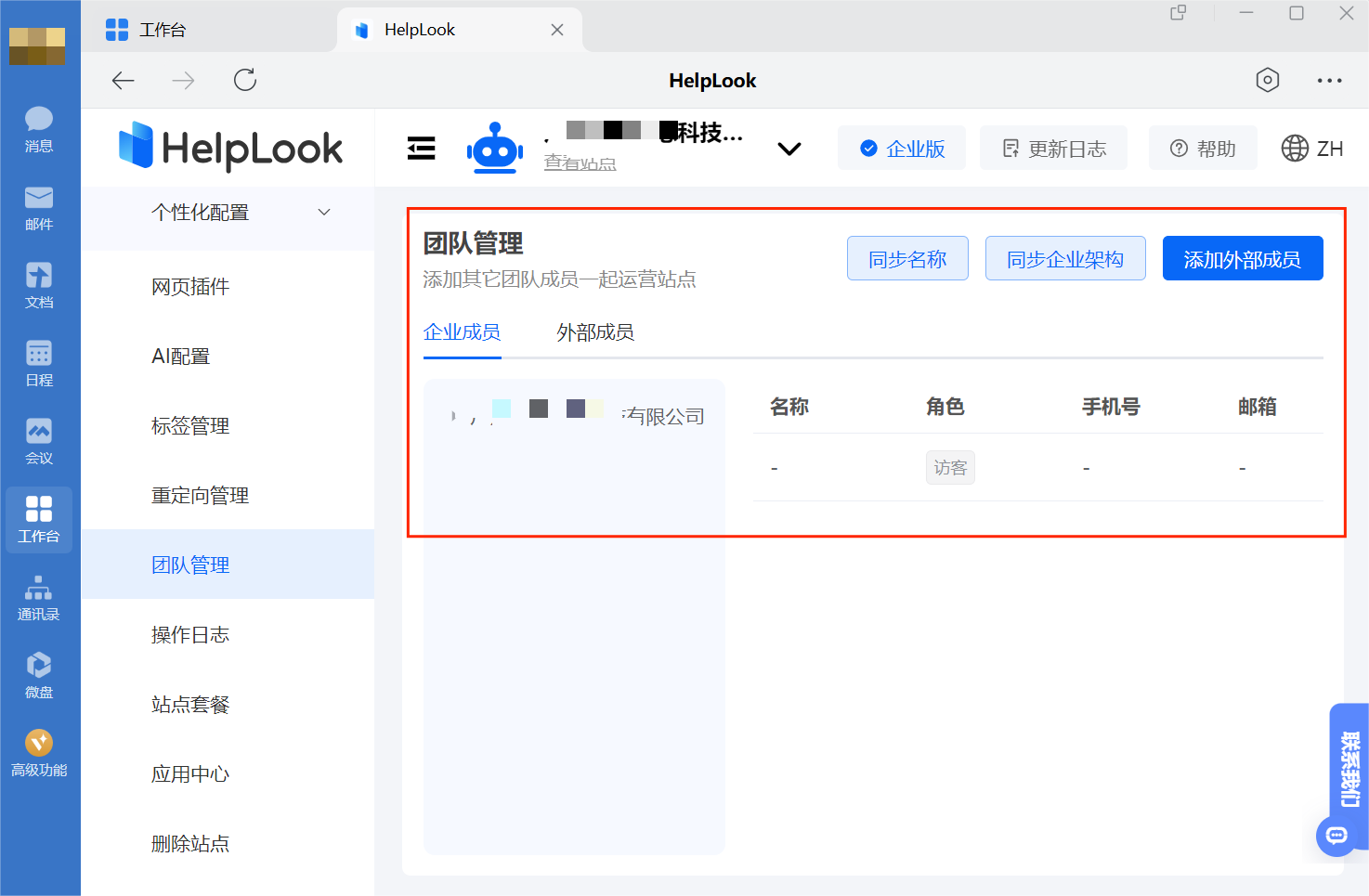
如果想将企业微信的组织架构同步到内部知识库咋搞?方法来也!
在现代企业的运营中,内部知识库不仅储存了公司的宝贵知识资产,还充当着员工信息共享和协作的核心平台。为了保障知识库的效能最大化,使其成为支持决策、创新和培训的强大工具,企业必须拥有一套周到的权限管理机制。对此࿰…...
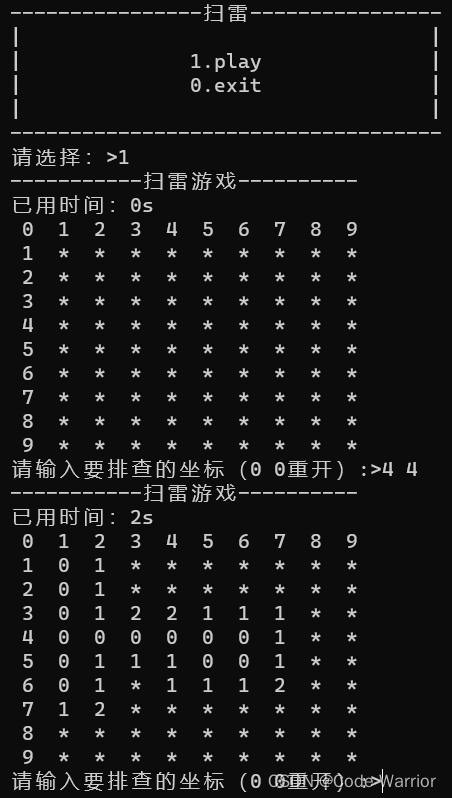
【c语言】扫雷
前言: 扫雷是一款经典的单人益智游戏,它的目标是在一个方格矩阵中找出所有的地雷,而不触碰到任何一颗地雷。在计算机编程领域,扫雷也是一个非常受欢迎的项目,因为它涉及到许多重要的编程概念,如数组、循环…...

自然语言处理的崛起:从初步分析到深度理解
自然语言处理(NLP)是计算机科学、人工智能和语言学的交叉领域,旨在让计算机能够理解和生成人类语言。随着时间的推移,NLP 经历了一系列革命性的变化,从简单的规则和模式匹配到如今的深度学习模型,它们使计算…...

Git学习笔记:版本回滚
文章目录 回到过去:开启新时间线,时间分叉路口1. 回溯开发2. 临时恢复特性3. 实验性开发4. 分支维护和发布5. 调试历史问题类比推理: 方法:1. 临时查看旧版本2. 永久回滚到旧版本3. 创建新的分支指向旧版本 回到过去:开…...

OpenCV图像的基本操作
图像的基本操作(Python) 素材图 P1:die.jpg P2:cool.jpg V:rabbit.mp4, 下载地址 读取展示-图像 import cv2img_1 cv2.imread(./die.jpg) # default cv2.IMREAD_COLOR print("die.jpg shape(imre…...

小白水平理解面试经典题目LeetCode 594 Longest Harmonious Subsequence(最大和谐字符串)
594 最大和谐字符串 这道题属于字符串类型题目,解决的办法还是有很多的,暴力算法,二分法,双指针等等。 题目描述 和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。 现在,给你一个整数数组 nums …...
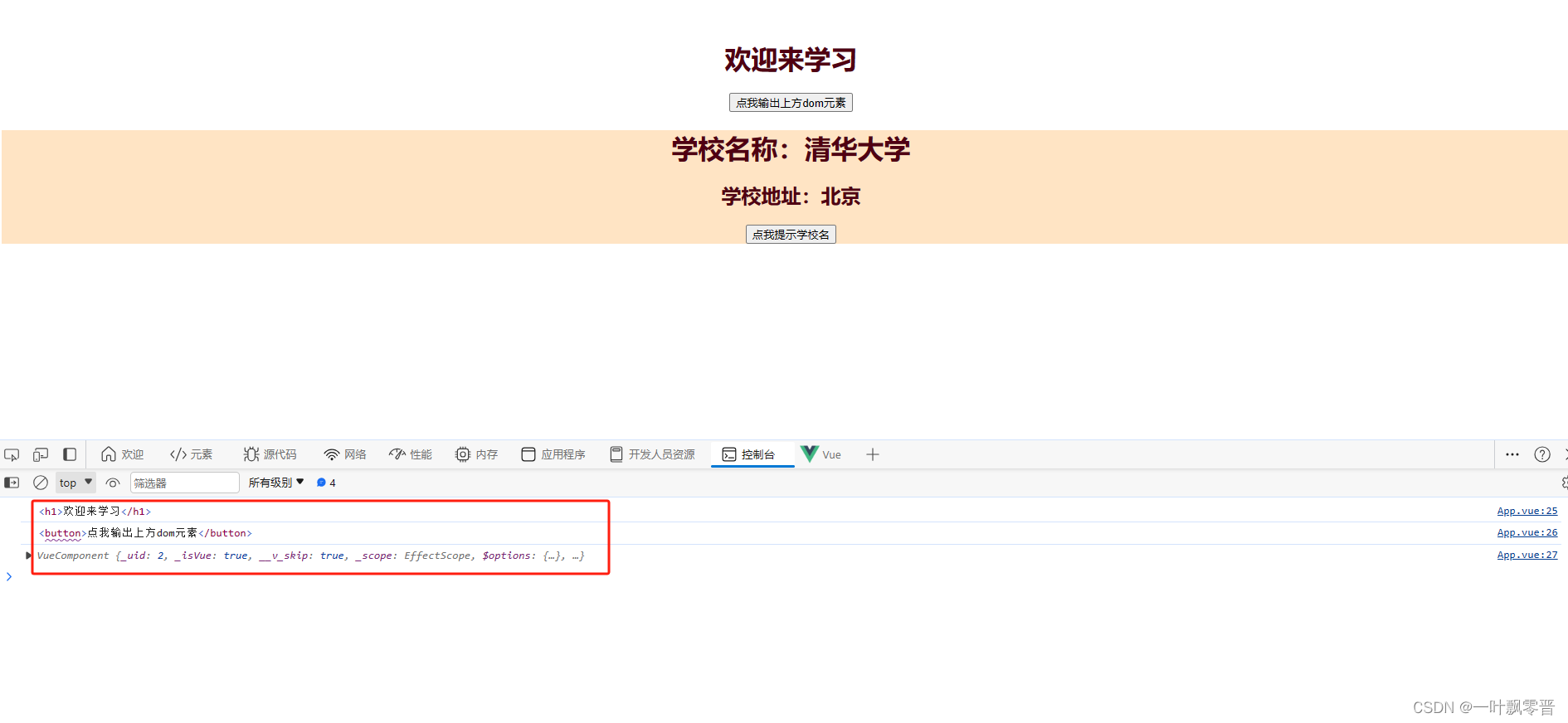
Vue-35、Vue中使用ref属性
1、ref属性 2、代码 <template><div id"app"> <!-- <img alt"Vue logo" src"./assets/logo.png">--><h1 v-text"msg" ref"title"></h1><button click"showDOM" ref&…...
网络通信(15)-C#TCP客户端掉线重连实例
本文上接前面的文章使用Socket在C#语言环境下完成TCP客户端的掉线重连实例。 掉线重连需要使用心跳包发送测试网络的状态,进而进入重连循环线程。 前面实例完成的功能: 客户端与服务器连接,实现实时刷新状态。 客户端接收服务器的数据。 客户端发送给服务器的数据。 客…...
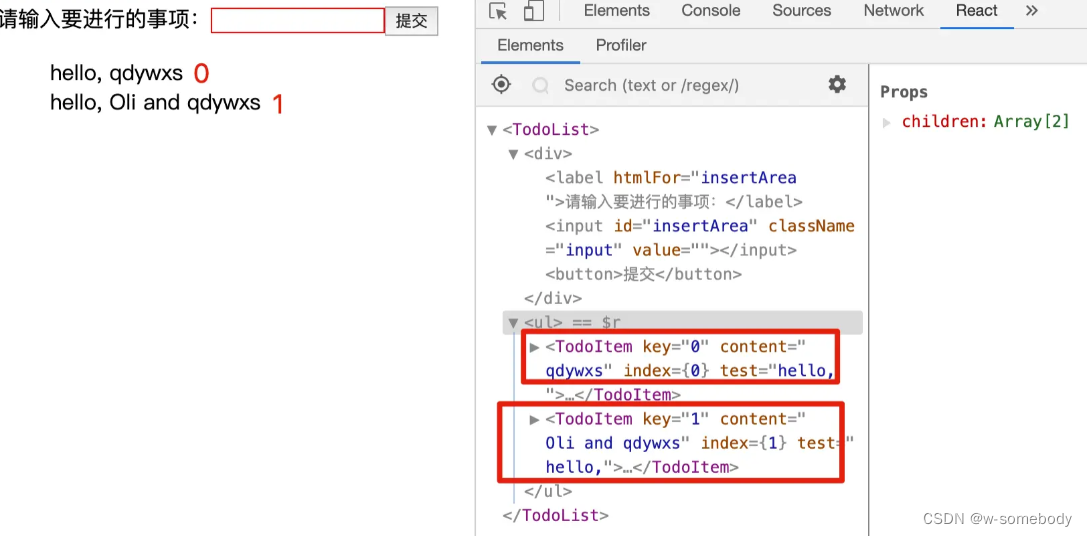
React进阶 - 14(说一说”虚拟DOM“中的”Diff算法“)
本章内容 目录 一、了解 Diff 算法二、key 值的重要性三、为什么不建议使用 index 做 key 值 上一节我们初步了解了 React中的”虚拟 DOM“ ,本节我们来说一说”虚拟DOM“中的”Diff算法“ 一、了解 Diff 算法 在上一篇中,我们有讲到:当 st…...

#GPU|LLM|AIGC#集成显卡与独立显卡|显卡在深度学习中的选择与LLM GPU推荐
区别 核心区别:显存,也被称作帧缓存。独立显卡拥有独立显存,而集成显卡通常是没有的,需要占用部分主内存来达到缓存的目的 集成显卡: 是集成在主板上的,与主处理器共享系统内存。 一般会在很多轻便薄型的…...

HCIP-IPV6实验
实验拓扑 实验需求 全网可达 实验思路 配置IP地址 配置路由协议-ospf 配置R2 配置IPV6 配置R2Tunnel 将所有地址引流到Tunnel0/0/0接口 ripng配置 汇总 实验步骤 配置IP地址 以R2为例 [Huawei]sys r2 [r2]int g0/0/0 [r2-GigabitEthernet0/0/0]ip address 12.1.1…...

如何训练和导出模型
介绍如何通过DI-engine使用DQN算法训练强化学习模型 一、什么是DQN算法 DQN算法,全称为Deep Q-Network算法,是一种结合了Q学习(一种价值基础的强化学习算法)和深度学习的算法。该算法是由DeepMind团队在2013年提出的,…...

Springboot注解@Aspect(一)之@Aspect 作用和Aop关系详解
目录 Aspect的使用 配置 作用 通知相关的注解 例子 结果: Aspect作用和Spring Aop关系 示例 标签表达式 Aspect的使用 配置 要启用 Spring AOP 和 Aspect 注解,需要在 Spring 配置中启用 AspectJ 自动代理,但是在 Spring Boot 中&a…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
