Offer必备算法_二分查找_八道力扣OJ题详解（由易到难）

目录

二分查找算法原理

①力扣704. 二分查找

解析代码

②力扣34. 在排序数组中查找元素的第一个和最后一个位置

解析代码

③力扣69. x 的平方根 

解析代码

④力扣35. 搜索插入位置

解析代码

⑤力扣852. 山脉数组的峰顶索引

解析代码

⑥力扣162. 寻找峰值

解析代码

⑦力扣153. 寻找旋转排序数组中的最小值

解析代码

⑧力扣LCR 173. 点名

解析代码

本篇完。

---

二分查找算法原理

        二分查找一种效率较高的查找方法。已经有严谨的数学证明其时间复杂度是O（logN），如果在全国14亿人口中找一个人，那么只需查找31次，但是，二分查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列（无序有时也行，但是要有二段性）。一般步骤如下：

        首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

以前学C/C++也写过二分查找的代码，直接刷题：

①力扣704. 二分查找

704. 二分查找 - 力扣（LeetCode）

难度 简单

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

class Solution {
public:int search(vector<int>& nums, int target) {}
};

---

解析代码

首先是有序的，就知道用二分，且这是一道朴素的二分（后面有不朴素的），简单题重拳出击：

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while(left <= right){int mid = left + (right - left) / 2;if(nums[mid] > target){right = mid - 1;}else if(nums[mid] < target){left = mid + 1;}else{return mid;}}return -1;}
};

---

②力扣34. 在排序数组中查找元素的第一个和最后一个位置

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

难度 中等

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 10^5
• -10^9 <= nums[i] <= 10^9
• nums 是一个非递减数组
• -10^9 <= target <= 10^9

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {}
};

---

解析代码

非递减，就是数组往后都是大于或者等于的元素，用暴力解法就是找到随便一个端点元素，然后往前往后线性遍历，极端时间复杂度还是O（N），这里用进阶二分的套路（等下总结）

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int size = nums.size();if(size == 0) // 处理边界return {-1, -1}; //返回一个vector里两个整数的方式int left = 0, right = size - 1; // 找左端点while(left < right) // 一定是小于{int mid = left + (right - left) / 2; // 元素个数是偶数时，中点是中间的左边if(nums[mid] < target) // 左端点肯定不在左边left = mid + 1;elseright = mid; // 可能自己是左端点，可能左端点还在左边}if(nums[left] != target) // 没有端点的情况return {-1, -1};int tmp = left; // 记录左端点right = size - 1; // 找右端点，left不用重置while(left < right){int mid = left + (right - left + 1) / 2; // 元素个数是偶数时，中点是中间的右边if(nums[mid] > target) // 右端点肯定右在左边right = mid -1;elseleft = mid; // 可能自己是右端点，可能右端点还在右边}return {tmp, right};}
};

以后二分大部分题目都是这个进阶二分的套路，套路就是这样的了（注意两个while的比较）：

        int left = 0, right = size - 1; // 找左端点while(left < right) // 一定是小于{int mid = left + (right - left) / 2; // 元素个数是偶数时，中点是中间的左边if(nums[mid] < target) // 左端点肯定不在左边left = mid + 1;elseright = mid; // 可能自己是左端点，可能左端点还在左边}if(nums[left] != target) // 没有端点的情况return {-1, -1};int tmp = left; // 记录左端点right = size - 1; // 找右端点，left不用重置while(left < right){int mid = left + (right - left + 1) / 2; // 元素个数是偶数时，中点是中间的右边if(nums[mid] > target) // 右端点肯定右在左边right = mid -1;elseleft = mid; // 可能自己是右端点，可能右端点还在右边}return {tmp, right};

---

③力扣69. x 的平方根 

69. x 的平方根 - 力扣（LeetCode）

难度 简单

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

• 0 <= x <= 2^31 - 1

class Solution {
public:int mySqrt(int x) {}
};

---

解析代码

暴力解法可以遍历1到X / 2的所有整数，因为这段整数是有序的，所有可以用二分算法，用上一题力扣34总结的进阶二分套路，求右端点：

class Solution {
public:int mySqrt(int x) {if(x <= 1) // 看给的范围处理边界{return x / 1; // 如果是1的话下面right就是0了}int left = 0, right = x / 2;while(left < right){long long mid = left + (right - left + 1) / 2;if(mid * mid > x) // 开long long防溢出{right = mid - 1;}else{left = mid;}}return right;}
};

---

④力扣35. 搜索插入位置

35. 搜索插入位置 - 力扣（LeetCode）

难度 简单

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums 为 无重复元素 的 升序 排列数组
• -10^4 <= target <= 10^4

class Solution {
public:int searchInsert(vector<int>& nums, int target) {}
};

---

解析代码

明显的二分查找，且找左端点：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;if(nums[right] < target) // 找不到就尾插{return right + 1;}while(left < right) // 找不到target就找一个比target大的值，插入到它的前面{int mid = left + (right - left) / 2; // 根据上面注释用二分中找左端点的套路if(nums[mid] < target){left = mid + 1;}else{right = mid;}}return left; // 找没找到都是返回left下标}
};

---

⑤力扣852. 山脉数组的峰顶索引

852. 山脉数组的峰顶索引 - 力扣（LeetCode）

LCR 069. 山脉数组的峰顶索引 - 力扣（LeetCode）

难度 中等

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums 为 无重复元素 的 升序 排列数组
• -10^4 <= target <= 10^4

class Solution {
public:int searchInsert(vector<int>& nums, int target) {}
};

---

解析代码

虽然整个数组不是有序的，但是根据单调性可以分出二段性。这里利用二段性把mid归到递增部分，下面就是找右端点：

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {// 虽然整个数组不是有序的，但是根据单调性可以分出二段性// 这里利用二段性把mid归到递增部分，下面就是找右端点：int left = 0, right = arr.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] < arr[mid - 1]) // 如果是递减部分{right = mid - 1;}else{left = mid;}}return left;}
};

---

⑥力扣162. 寻找峰值

162. 寻找峰值 - 力扣（LeetCode）

难度 中等

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。

提示：

• 1 <= nums.length <= 1000
• -2^31 <= nums[i] <= 2^31 - 1

class Solution {
public:int findPeakElement(vector<int>& nums) {}
};

---

解析代码

        注意到是返回任意个峰值都可以，就类似数学的求极大值，那问题就变成上一题力扣852. 山脉数组的峰顶索引了，直接把nums参数改成arr然后复制上一题代码过来就AC了，二段性就是如果找到一个点，如果这个点的右边元素比它小，那么一定有一个极大值在它左边。反之极大值在它右边或者它就是极大值。

class Solution {
public:int findPeakElement(vector<int>& arr) {// 虽然整个数组不是有序的，但是根据单调性可以分出二段性// 这里利用二段性把mid归到递增部分，下面就是找右端点：int left = 0, right = arr.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] < arr[mid - 1]) // 如果是递减部分{right = mid - 1;}else{left = mid;}}return left;}
};

---

⑦力扣153. 寻找旋转排序数组中的最小值

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

难度 中等

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 3 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

class Solution {
public:int findMin(vector<int>& nums) {}
};

---

解析代码

 二段性就是以最右边元素（下图为D）为标志，如果一个点比它大，那么找的元素肯定在另一边，

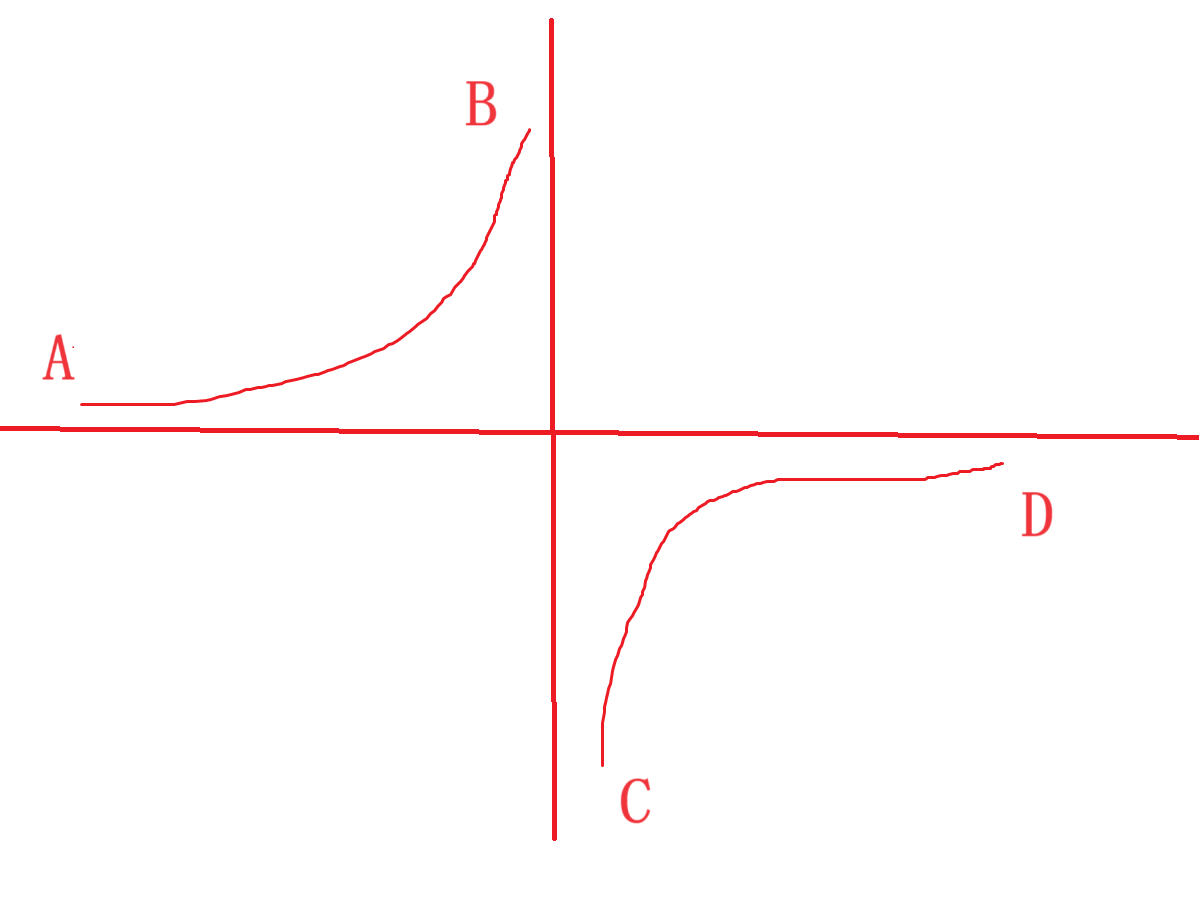
以A为标志也行，但是有边界情况要处理，下面就以D为标志，找左端点：

class Solution {
public:int findMin(vector<int>& nums) {// 二段性就是以最右边元素为标志，如果一个点比它大，那么找的元素肯定在另一边// 以下就是二分找左端点的套路int left = 0, right = nums.size() - 1;int tmp = right;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[tmp]) // 如果是递减部分{left = mid + 1;}else{right = mid;}}return nums[left];}
};

---

⑧力扣LCR 173. 点名

LCR 173. 点名 - 力扣（LeetCode）

难度 简单

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

示例 1:

输入: records = [0,1,2,3,5]
输出: 4

示例 2:

输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
输出: 7

提示：

1 <= records.length <= 10000

class Solution {
public:int takeAttendance(vector<int>& records) {}
};

---

解析代码

此题就是以前写过的剑指Offer中数组消失的数字，解法有哈希，遍历，位运算，数学求和，时间都是O（N），二分的解法是O（logN）。

二段性就是找的元素的值肯定不等于数组下标，求左端点的套路：

class Solution {
public:int takeAttendance(vector<int>& records) {// 解法有哈希，遍历，位运算，数学求和，时间都是O（N），二分的解法是O（logN）// 此题二段性就是找的元素的值肯定不等于数组下标，求左端点的套路int left = 0, right = records.size() - 1;if(records[right] == right){return right + 1;}while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid){left = mid + 1;}else{right = mid;}}return records[left] - 1;}
};

---

本篇完。

下一部分是前缀和算法。