【格密码基础】:补充LWE问题
目录
一. LWE问题的鲁棒性
二. LWE其他分布选择
三. 推荐文献
四. 附密码学人心中的顶会
一. LWE问题的鲁棒性
robustness,翻译为鲁棒性
已有的论文表明,及时敌手获取到部分关于秘密和error的信息,LWE问题依旧是困难的,这能体现出该问题的鲁棒性。
在2010年,Goldwasser等人发现,如果限定秘密的模长,或者将关于秘密的很难求逆的函数值(类似单向函数)告诉敌手,该问题的困难性和原始的LWE问题是一样的。在实际证明归约的过程中,维度n和误差率都是相对较小的。基于此理论可以设计一个对称的密码(symmetric-key encryption)方案,其允许密钥不太完美或者被泄露部分信息。
如果给出计算意义上很难求逆的单向函数值,2010年Dodis证明即使如此依旧可以基于LWE问题设计公钥密码方案。
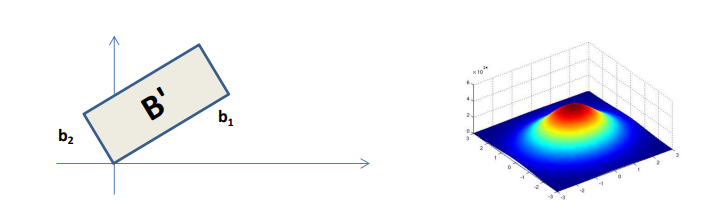
在后来的工作中,人们陆续发现了LWE问题的鲁棒性提现:忽略维度和误差率(error rate)的变化,及时秘密和error的部分线性关系被泄露,LWE问题依旧是可证明安全的。
二. LWE其他分布选择
回顾LWE问题我们发现,其error的选择有两个要点:1.来源高斯分布;2.值相对较小。那么现在我们就在想,error能不能来自于其他分布,比如说在某个区间上的均匀分布呢?
在2013年,有两篇相关的工作,一个是Dottling-Muller,另一个是Micciancio-Peikert。这些人都证明了选择其他非高斯分布也是可以的。
选其他分布会比高斯分布更好吗?
从算法设计的层面来讲,像均匀分布比高斯分布更容易实现,所以在网络安全领域更加具有应用价值。
在2011年,Arora 和Ge发现,如果把error的尺寸范围设定为d,那么解决LWE问题的时间和空间复杂度为:
这显然给LWE问题的困难性证明带来了极大的挑战,好在这类攻击算法要求给定的LWE样本足够多。
接下里我们将简短解释LWE的样本个数如何影响问题的困难性。
对于非高斯分布的error(比如说可以选择均匀分布),哪怕error选取的空间很小,比如只能取0或1,也就是:
只要给与敌手的样本个数为m是有上限的,那么LWE问题依旧是困难的。如果将该上限去掉的话,那么根据Arora-Ge攻击算法,LWE问题可直接被攻破。举几个简单的例子。
如果error只是简单的二进制,那么样本个数需要限定为:
![]()
如果error的尺寸放宽到:
![]()
那么样本个数也可以放宽到:
![]()
其实有点惊讶,当error只取0或1时,LWE问题也是困难的。但是其样本个数太少了,导致很难利用其设计密码系统。
已有的研究表明,先从足够大的高斯error中选取,再形成标准的LWE分布,然后再调整更大的维度,再将此分布作为后续search-LWE问题中的ai,那么形成的新问题在信息论(information-theoretically)上是无法解决的。此时的ai选择并不是真的随机分布,问题变得更加困难了。要想证明其安全性的话,也比较直接。因为标准的LWE分布与均匀分布之间是不可区分的,只要标准的decision-LWE问题困难,那么小-error版本的LWE问题也就是困难的。
三. 推荐文献
(1)总结LWE与SIS问题
D. Micciancio and C. Peikert. Hardness of SIS and LWE with small parameters. In CRYPTO,
pages 21–39. 2013.
(2)攻击LWE问题
S. Arora and R. Ge. New algorithms for learning in presence of errors. In ICALP (1), pages
403–415. 2011.
(3)证明LWE问题的鲁棒性
S. Ling, D. H. Phan, D. Stehle, and R. Steinfeld. Hardness of ´ k-LWE and applications in traitor
tracing. In CRYPTO, pages 315–334. 2014.
四. 附密码学人心中的顶会
(1)欧密
会议简称:EUROCRYPT
会议全称:International Conference on the Theory and Applications of Cryptographic Techniques
出版社:Springer
(2)美密
会议简称:CRYPTO
会议全称:International Cryptology Conference
出版社:Springer
(3)亚密
会议简称:ASIACRYPT
会议全称:Annual International Conference on the Theory and Application of Cryptology and Information Security
出版社:Springer
(4)CHES
会议简称:CHES
会议全称:International Conference on Cryptographic Hardware and Embedded Systems
出版社:Springer
(5)PKC
会议简称:PKC
会议全称:International Workshop on Practice and Theory in Public Key Cryptography
出版社:Springer
相关文章:
【格密码基础】:补充LWE问题
目录 一. LWE问题的鲁棒性 二. LWE其他分布选择 三. 推荐文献 四. 附密码学人心中的顶会 一. LWE问题的鲁棒性 robustness,翻译为鲁棒性 已有的论文表明,及时敌手获取到部分关于秘密和error的信息,LWE问题依旧是困难的,这能…...

【C++入门到精通】特殊类的设计 |只能在堆 ( 栈 ) 上创建对象的类 |禁止拷贝和继承的类 [ C++入门 ]
阅读导航 引言一、特殊类 --- 不能被拷贝的类1. C98方式:2. C11方式: 二、特殊类 --- 只能在堆上创建对象的类三、特殊类 --- 只能在栈上创建对象的类四、特殊类 --- 不能被继承的类1. C98方式2. C11方法 总结温馨提示 引言 在面向对象编程中࿰…...
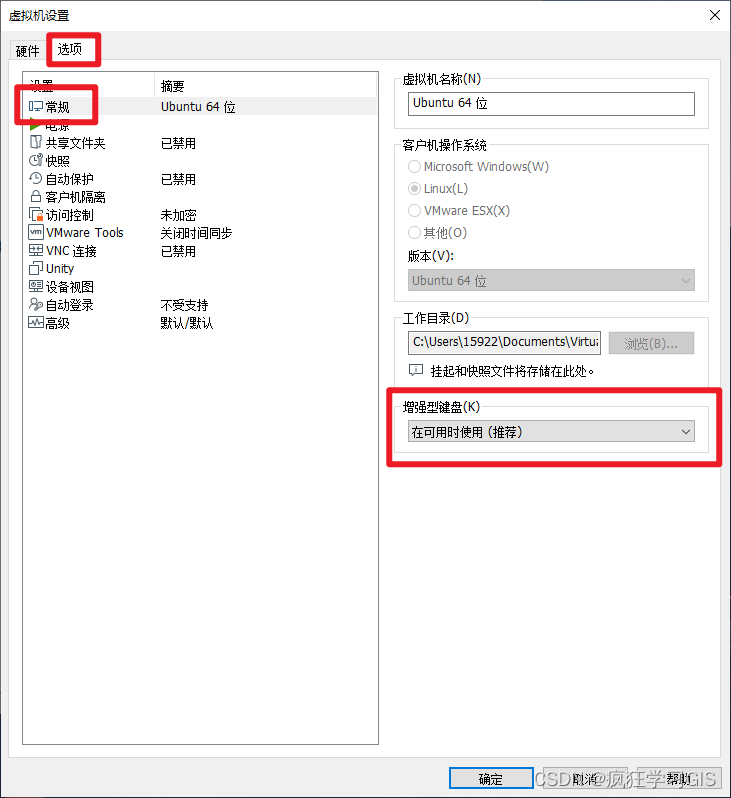
VMware虚拟机部署Linux Ubuntu系统
本文介绍基于VMware Workstation Pro虚拟机软件,配置Linux Ubuntu操作系统环境的方法。 首先,我们需要进行VMware Workstation Pro虚拟机软件的下载与安装。需要注意的是,VMware Workstation Pro软件是一个收费软件,而互联网中有很…...

RFID标签:数字时代的智能身份
在数字时代,RFID标签(Radio-Frequency Identification)成为物联网(IoT)中不可或缺的一环。作为一种小巧却功能强大的设备,RFID标签在各个领域的应用不断扩展,为我们的生活和工作带来了新的可能性…...
》笔记3.2)
《动手学深度学习(PyTorch版)》笔记3.2
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...
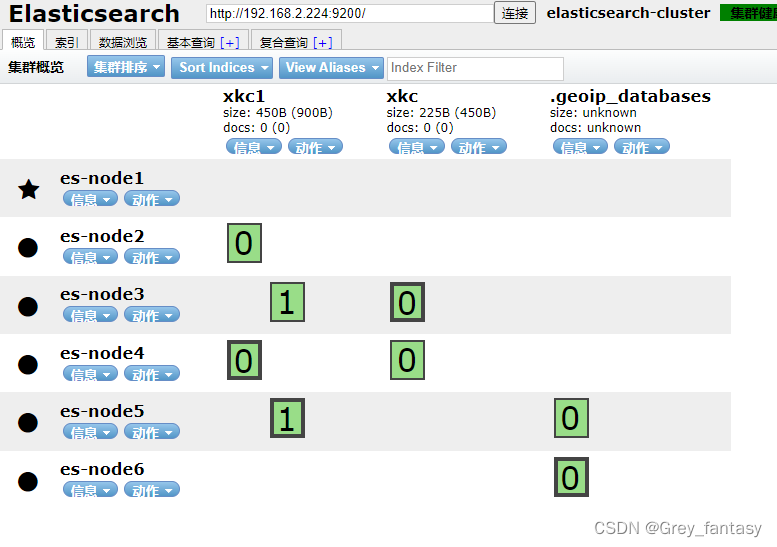
elasticsearch8.x版本docker部署说明
前提,当前部署没有涉及证书和https访问 1、环境说明,我采用三个节点,每个节点启动两个es,用端口区分 主机角色ip和端口服务器Amaster192.168.2.223:9200服务器Adata192.168.2.223:9201服务器Bdata,master192.168.2.224:9200服务器Bdata192.1…...

使用scyllaDb 或者cassandra存储聊天记录
一、使用scyllaDb的原因 目前开源的聊天软件主要还是使用mysql存储数据,数据量大的时候比较麻烦; 我打算使用scyllaDB存储用户的聊天记录,主要考虑的优点是: 1)方便后期线性扩展服务器; 2)p…...
Visual Studio如何修改成英文版
1、打开 Visual Studio Installer 2、点击修改 3、找到语言包,选择需要的语言包,而后点击修改 4、等待下载 5、 安装完成后启动Visual Studio 6、在工具-->选项-->环境-->区域设置-->English并确定 7、重启 Visual Studio,配置…...
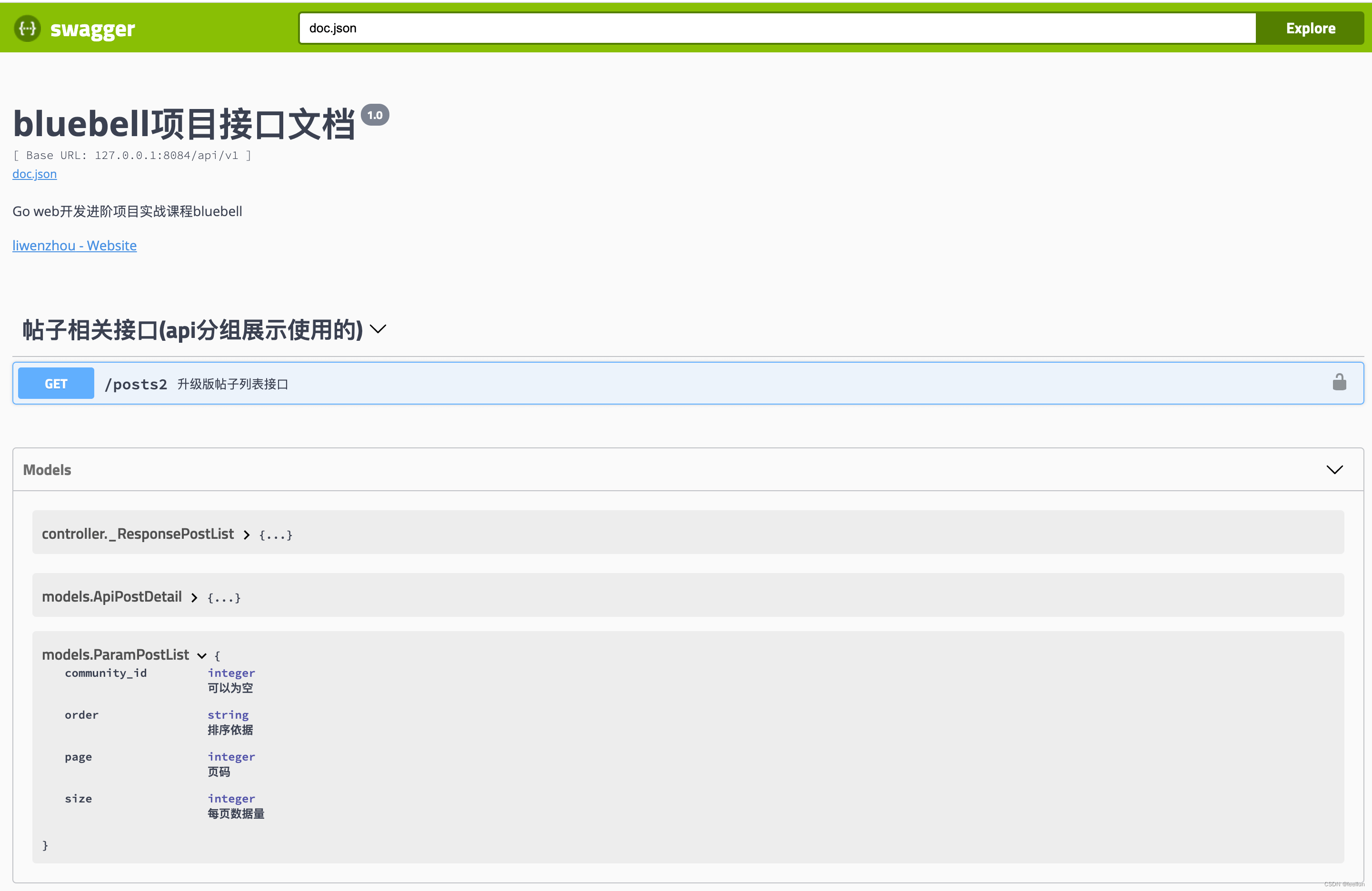
gin中使用swagger生成接口文档
想要使用gin-swagger为你的代码自动生成接口文档,一般需要下面三个步骤: 按照swagger要求给接口代码添加声明式注释,具体参照声明式注释格式。使用swag工具扫描代码自动生成API接口文档数据使用gin-swagger渲染在线接口文档页面 第一步&…...
最新AI创作系统ChatGPT网站系统源码,Midjourney绘画V6 ALPHA绘画模型,ChatFile文档对话总结+DALL-E3文生图
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧。已支持GPT…...

解析dapp:从底层区块链看DApp的脆弱性和挑战
每天五分钟讲解一个互联网只是,大家好我是啊浩说模式Zeropan_HH 在Web3时代,去中心化应用程序(DApps)已成为数字经济的重要组成部分。它们的同生性,即与底层区块链网络紧密相连、共存亡的特性,为DApps带来…...

机器学习整理
绪论 什么是机器学习? 机器学习研究能够从经验中自动提升自身性能的计算机算法。 机器学习经历了哪几个阶段? 推理期:赋予机器逻辑推理能力 知识期:使机器拥有知识 学习期:让机器自己学习 什么是有监督学习和无监…...
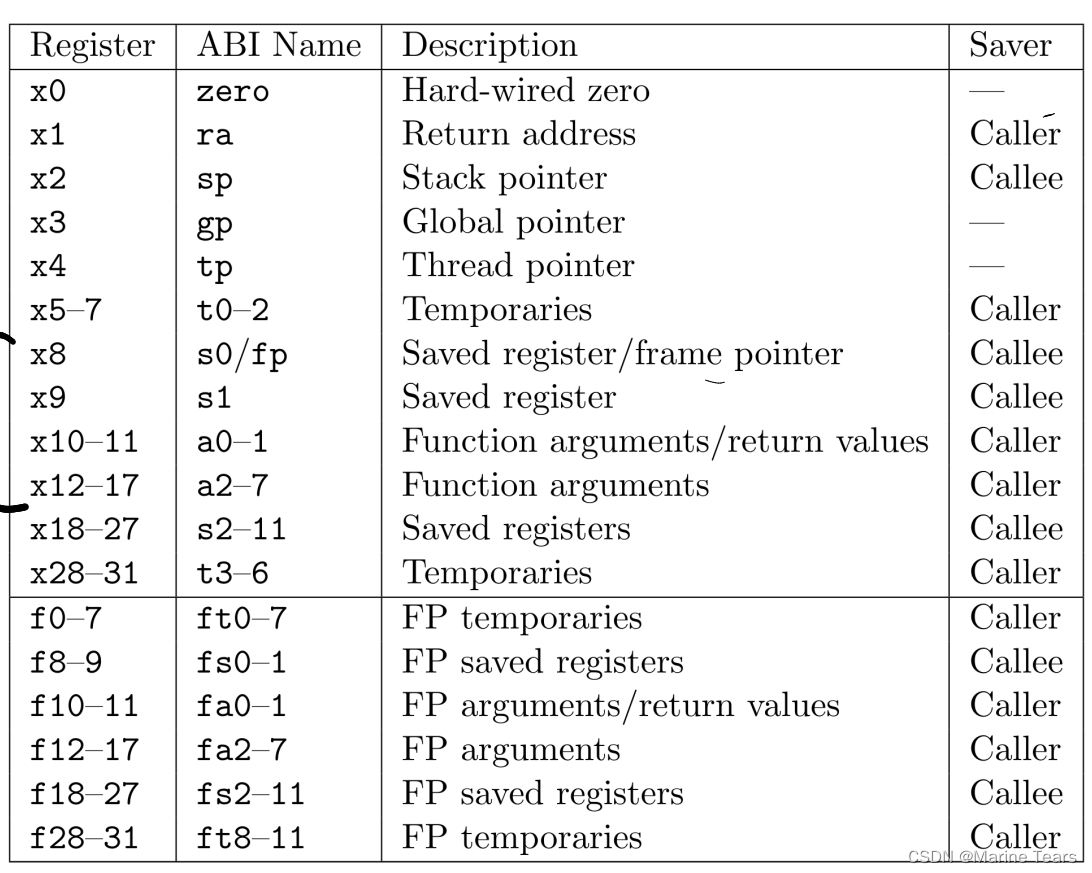
RISC-V常用汇编指令
RISC-V寄存器表: RISC-V和常用的x86汇编语言存在许多的不同之处,下面将列出其中部分指令作用: 指令语法描述addiaddi rd,rs1,imm将寄存器rs1的值与立即数imm相加并存入寄存器rdldld t0, 0(t1)将t1的值加上0,将这个值作为地址,取…...
第二篇:数据结构与算法-链表
概念 链表是线性表的链式存储方式,逻辑上相邻的数据在计算机内的存储位置不必须相邻, 可以给每个元素附加一个指针域,指向下一个元素的存储位 置。 每个结点包含两个域:数据域和指针域,指针域存储下一个结点的地址&…...

低代码配置-小程序配置
数据结构 {"data": {"layout": {"api":{"pageApi":{//api详情}},"config":{"title":"页面标题",},"listLayout": {"fields": [{"componentCode": "grid…...

第十八讲_HarmonyOS应用开发实战(实现电商首页)
HarmonyOS应用开发实战(实现电商首页) 1. 项目涉及知识点罗列2. 项目目录结构介绍3. 最终的效果图4. 部分源码展示 1. 项目涉及知识点罗列 掌握HUAWEI DevEco Studio开发工具掌握创建HarmonyOS应用工程掌握ArkUI自定义组件掌握Entry、Component、Builde…...

OJAC近屿智能张立赛博士揭秘GPT Store:技术创新、商业模式与未来趋势
Look!👀我们的大模型商业化落地产品📖更多AI资讯请👉🏾关注Free三天集训营助教在线为您火热答疑👩🏼🏫 亲爱的伙伴们: 1月31日晚上8:30,由哈尔滨工业大学的…...

Java接收curl发出的中文请求无法解析
最近做项目遇到了这种情况,Java接收curl发出的中文请求无法解析,英文请求一切正常,中文请求则对方服务器无法解析,可以猜测是中文导致的编码问题,但是奇怪的是,本地输出json也没有乱码,编解码正…...

Java设计模式-外观模式(11)
大家好,我是馆长!今天开始我们讲的是结构型模式中的外观模式。老规矩,讲解之前再次熟悉下结构型模式包含:代理模式、适配器模式、桥接模式、装饰器模式、外观模式、享元模式、组合模式,共7种设计模式。。 外观模式(Decorator Pattern) 定义 外观(Facade)模式一种通…...
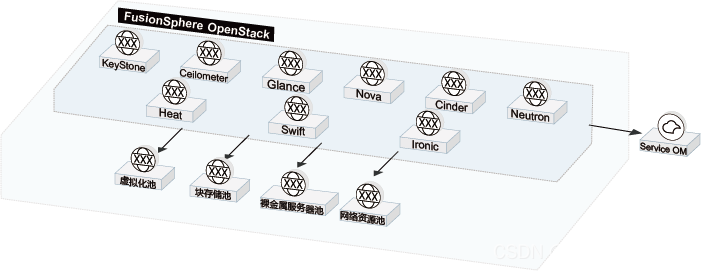
HCS-华为云Stack-FusionSphere
HCS-华为云Stack-FusionSphere FusionSphere是华为面向多行业客户推出的云操作系统解决方案。 FusionSphere基于开放的OpenStack架构,并针对企业云计算数据中心场景进行设计和优化,提供了强大的虚拟化功能和资源池管理能力、丰富的云基础服务组件和工具…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
