当前位置： 首页 > news >正文

Logistics 逻辑回归概念

news 2026/1/12 10:02:19

1. sigmoid函数

逻辑回归算法的拟合函数，叫做sigmoid函数：

函数图像如下（百度图片搜到的图）：

                

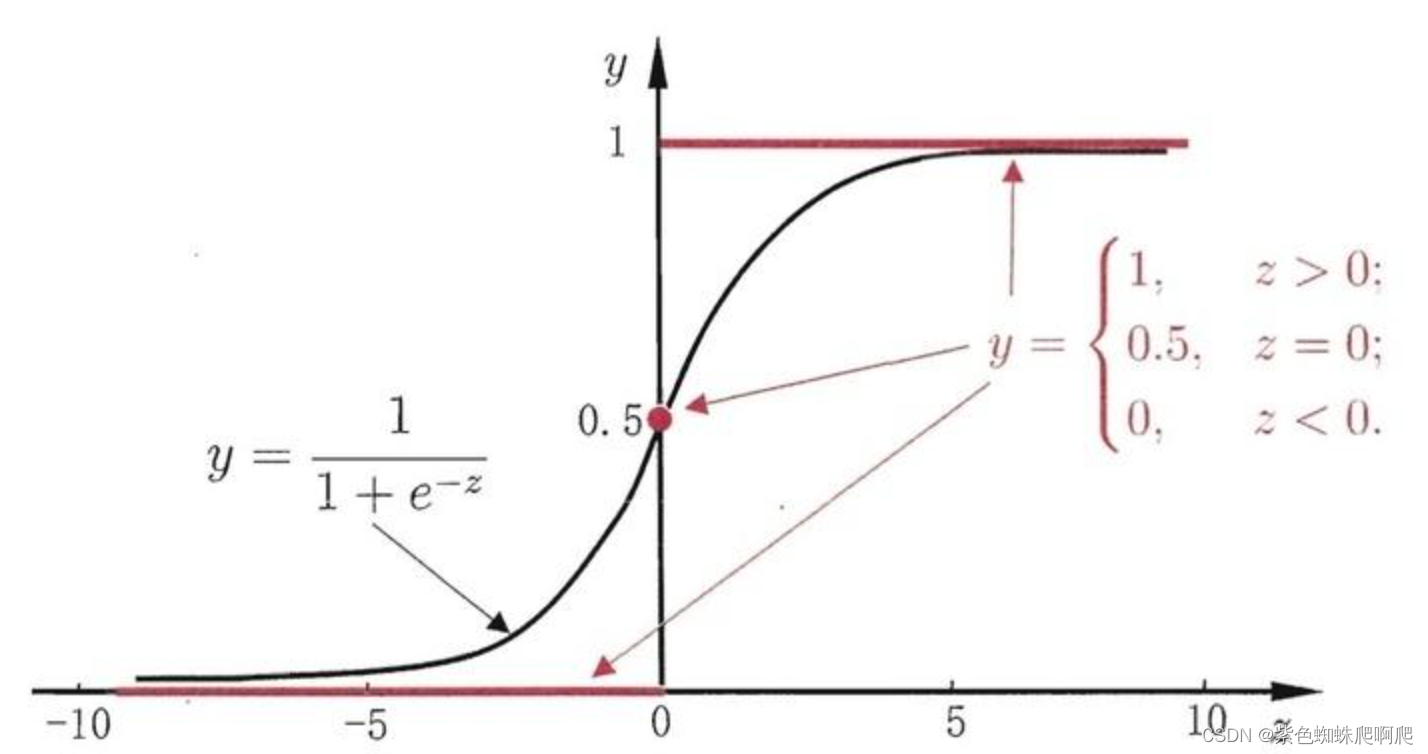
sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，而sigmoid有个平滑的过渡。

从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将x轴的取值范围(-无穷，+无穷)映射到函数值y的(0,1)之间，更适宜表示预测的概率，即事件发生的“可能性” 。

2. 逻辑回归出现的场景

2.1 研究线性回归

当我们研究相关性的时候，经常遇到线性关系，y与x为连续性变量，建立多元线性回归模型。

​​​​​​​2.2 遇到离散或者分类算法

有时候我们不是研究线性关系，而是研究是否取到红球，是否会变胖，是否会下单这样的分类或者离散问题。y为0/1离散变量时，不连续，上面的线性方程右侧是连续型，左侧现在变成离散型，无法建立线形回归模型。因此需要对方程进行logistic变化，或者叫做logistic映射。

​​​​​​​2.3 logistic映射

利用sigmoid函数，将上面的公式进行logistic映射：

  1. 理解sigmoid函数：当z取值越大，无穷大，e^{-z}越小，y越接近于1，反之，越接近于0。
  2. 理解带入z后的sigmoid函数：右侧是一个关于x的线性函数，x在（-无穷，+无穷）之间任意取值；左侧y是关于x的函数值，可以映射到[0,1]之间，也就是说我们现在利用逻辑回归将线性函数和分类/离散之间的关系解决了。
  3. 理解变形后的函数：根据上一篇最大似然估计，变形后的函数公式有利于去参数β。

3. 逻辑回归的概念

多重线性回归模型要求因变量是连续型的正态分布变量，且自变量与因变量呈线性关系。当因变量是分类变量，且自变量与因变量不呈线性关系时，就不能确足多重线性回归模型的适用条件。此时，处理该类问题常用Logistic回归模型。Logistic回归分析属于非线性回归，它是研究因变量为二项分类或多项分类结果与某些影响因素之间关系的一种多重回归分析方法。

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

本文用易于理解的方式介绍逻辑回归的概念，希望了解更多的推荐阅读 【机器学习】逻辑回归（非常详细） - 知乎

参考文档：

逻辑回归和优势比：大厂数据分析高频面试-逻辑回归和优势比2

最大似然和Logistics： 用人话讲明白逻辑回归Logistic regression - 知乎

logistics：【机器学习】逻辑回归（非常详细） - 知乎

logistics：经典Logistic回归：原理、计算步骤以及应用 - 知乎

相关文章：

Logistics 逻辑回归概念

1. sigmoid函数 逻辑回归算法的拟合函数，叫做sigmoid函数： 函数图像如下（百度图片搜到的图）： sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，…...

编程日记 2024/1/29 2:25:38

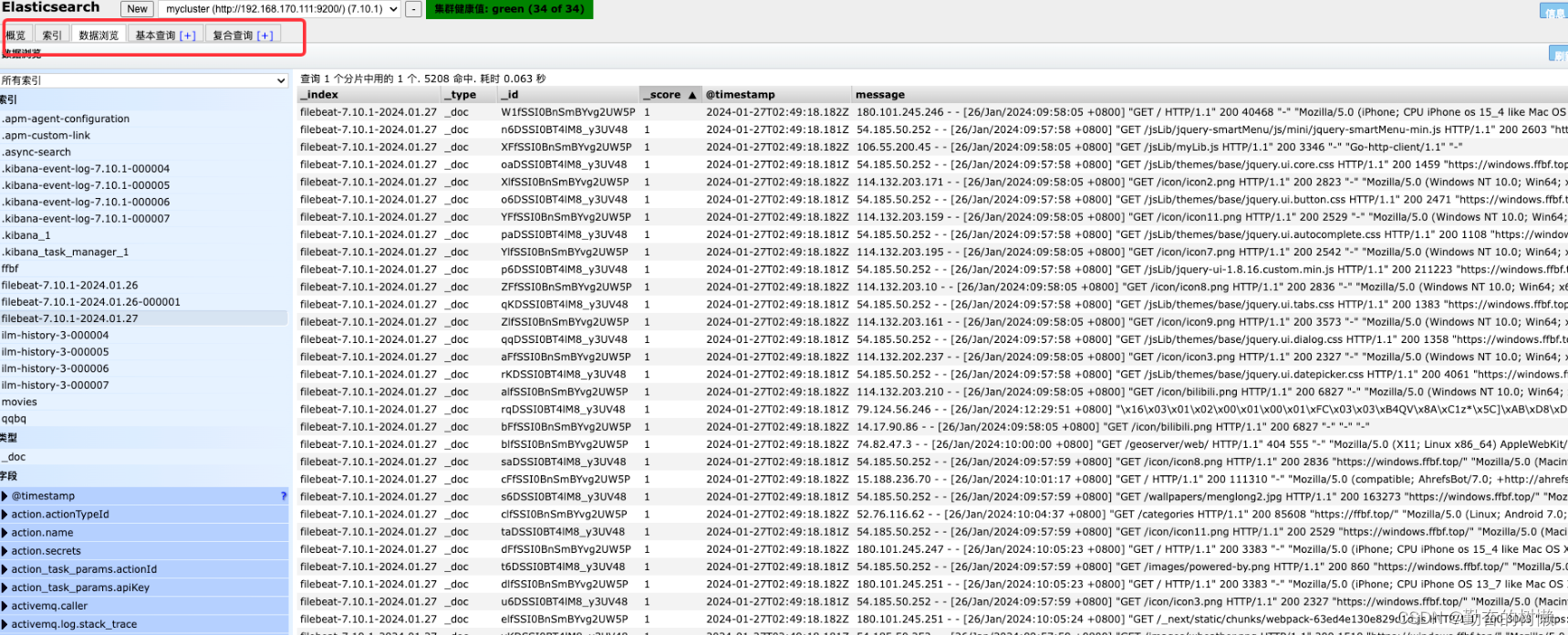
Elasticsearch安装Head图形插件

一、Google浏览器扩展插件方式 1.安装插件 进入谷歌浏览器应用商店搜索“Elasticsearch Head”，点击链接跳转 点击“添加至Chrome”按钮安装即可。 2.使用插件 在浏览器的插件列表多了个一个放大镜图标 点击“New”新建链接，输入es节点或集群地址。 连接成功 可以进行概括…...

编程日记 2024/1/29 2:17:31

【C++】——类和对象（中）

一、前言 好久没有更新内容了&#xff0c;今天为大家带来类和对形中期的内容 &#xff01; 二、正文 1.this指针 1.1this指针的引入 class Date { public:void Init(int year, int month, int day){_year year;_month month;_day day;}void Print(){cout << _year …...

编程日记 2024/1/29 2:13:27

uniapp组件库Card 卡片 的使用方法

目录 #平台差异说明 #基本使用 #配置卡片间距 #配置卡片左上角的缩略图 #配置卡片边框 #设置内边距 #API #Props #Slot #Event 卡片组件一般用于多个列表条目&#xff0c;且风格统一的场景。 #平台差异说明 AppH5微信小程序支付宝小程序百度小程序头条小程序QQ小程…...

编程日记 2024/1/29 2:12:26

一款强大的矢量图形设计软件：Adobe Illustrator 2023 (AI2023)软件介绍

Adobe Illustrator 2023 (AI2023) 是一款强大的矢量图形设计软件&#xff0c;为设计师提供了无限创意和畅行无阻的设计体验。AI2023具备丰富的功能和工具&#xff0c;让用户可以轻松创建精美的矢量图形、插图、徽标和其他设计作品。 AI2023在界面和用户体验方面进行了全面升级…...

编程日记 2024/1/29 2:10:25

对于循环的一次探索

写算法题的时候突然想到&#xff0c;为什么循环内定义变量不会算作是重复定义&#xff0c;以及变量作用域问题&#xff0c;为此&#xff0c;进行了一次探索 c&#xff1a; 代码&#xff1a; #include <stdio.h> int main() {int a 0;int* b &a;for (int i 0; i …...

编程日记 2024/1/29 2:09:24

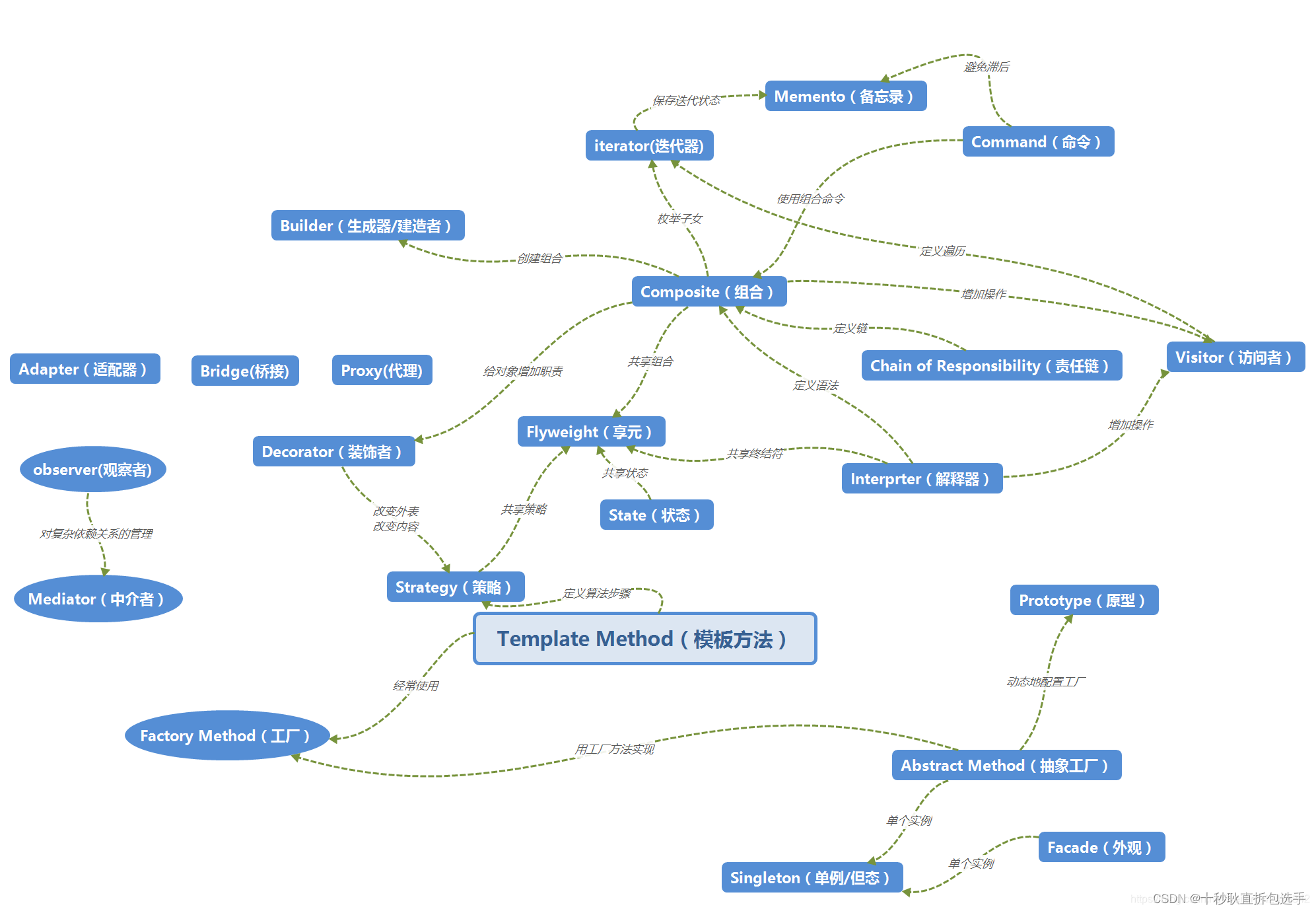
设计模式：简介及基本原则

简介 设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了重用代码、让代码更容易被他人理解、保证代码可靠性。 毫无疑问&#xff0c;设计模式于己于他人于系统都是多赢的&#xff0c;设计模式使代码编制真正工程化&#xff…...

编程日记 2024/1/29 2:07:22

营销领域有哪些著名的模型？如销售漏斗等

一、金字塔原理 模型 适用场景&#xff1a;提案 沟通 思考理论 模型 来源&#xff1a;麦肯锡 芭芭明托 1、表达的逻辑 遵循金字塔模型的逻辑&#xff0c;先说结论&#xff0c;后说论据。所有表达的内容都可归纳出一个核心论点。这个核心论点由N个论据作为支持&#xff0c;而…...

编程日记 2024/1/29 2:05:19

JavaScript学习-let、var、const的使用

let、var、const的使用 1.var var声明的变量会被提升到该作用域的顶部&#xff0c;若声明在函数内部&#xff0c;则他作用域在整个函数内部&#xff0c;即使他在函数末尾声明&#xff0c;在函数第一行也可以使用。声明在全局也是一样的。var不能声明常量&#xff0c;因为var可…...

编程日记 2024/1/29 2:04:18

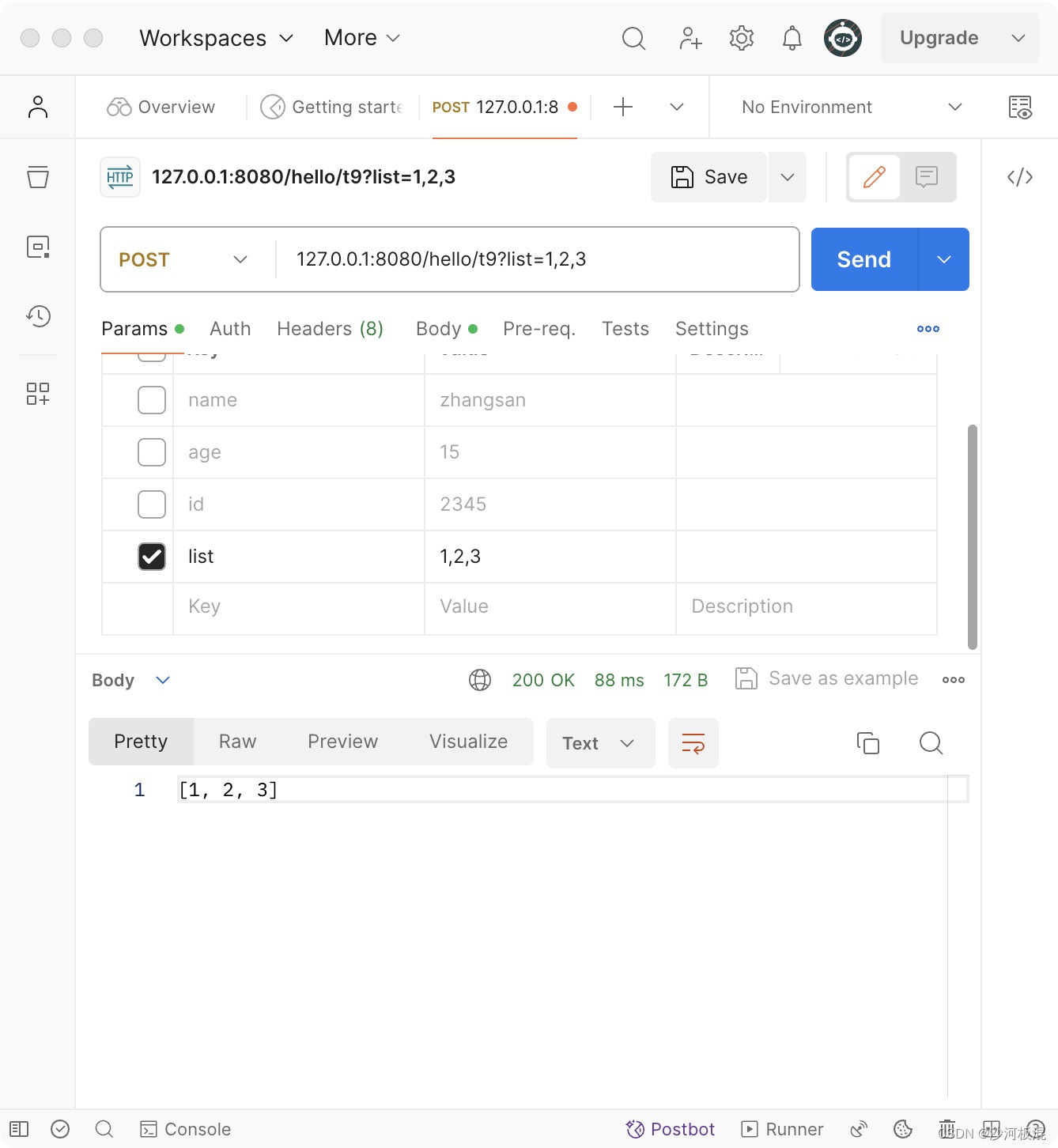
【Java】SpringMVC参数接收（一）

1、接收单个参数 &#xff08;1&#xff09;直接接收参数 RequestMapping("/hello") RestController public class HelloSpring {RequestMapping("/t2")public String t2(String name){return "name" name;} } 当没有传入参数时&#xff0c;返…...

编程日记 2024/1/29 1:58:14

File类知识点回顾

File类简介 File 是文件和目录路径名的抽象表示。 用户界面和操作系统使用依赖于系统的路径名字符串来命名文件和目录。 此类提供了一个抽象的&#xff0c;与系统无关的分层路径名视图。 抽象路径名有两个组成部分&#xff1a;可选系统有关的前缀字符串&#xff0c;如磁盘驱动…...

编程日记 2024/1/29 1:50:07

2024新版68套Axure RP大数据可视化大屏模板及通用组件+PSD源文件

Axure RP数据可视化大屏模板及通用组件库2024新版重新制作了这套新的数据可视化大屏模板及通用组件库V2版。新版本相比于V1版内容更加丰富和全面&#xff0c;但依然秉承“敏捷易用”的制作理念&#xff0c;这套作品也同样延续着我们对细节的完美追求&#xff0c;整个设计制作过…...

编程日记 2024/1/29 1:49:06

Optional lab: Linear Regression using Scikit-LearnⅠ

scikit-learn是一个开源的、可用于商业的机器学习工具包&#xff0c;此工具包包含本课程中需要使用的许多算法的实现 Goals In this lab you will utilize scikit-learn to implement linear regression using Gradient Descent Tools You will utilize functions from sci…...

编程日记 2024/1/29 1:46:03

CentOS使用

1.使用SSH连接操作虚拟机中的CentOS 使用代理软件(MobaX/Xshell)通过ssh连接vmware中的虚拟机,可以摆脱vmware笨重的软件,直接在代理软件中进行操作. 包括使用云虚拟器,其实也只是在本地通过ssh连接别处的云服务商的硬件而已. 1.1 配置静态IP 为什么要配置静态IP? 想要使用…...

编程日记 2024/1/29 1:45:02

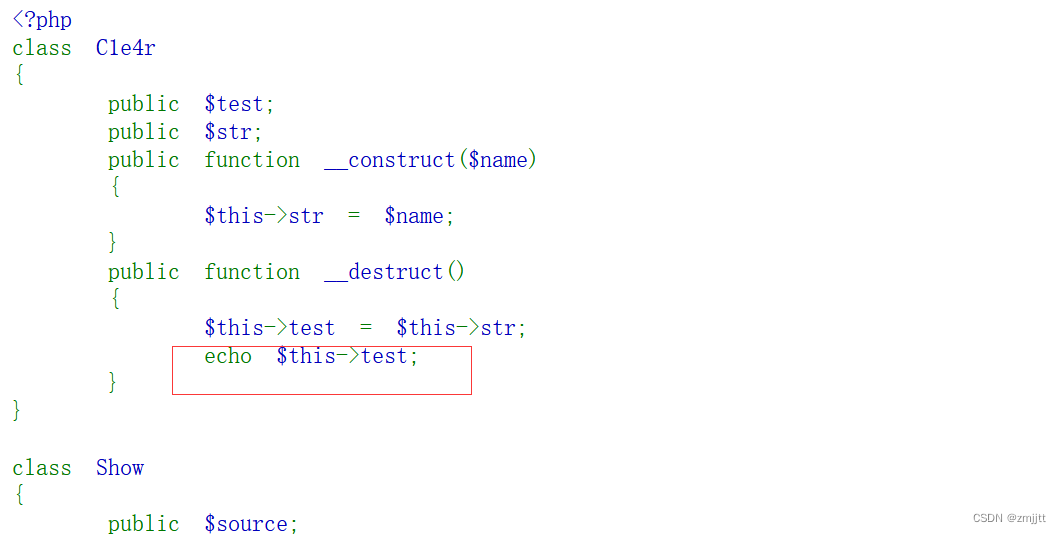
[SWPUCTF 2018]SimplePHP1

打开环境 有查看文件跟上传文件&#xff0c;查看文件里面显示没有文件url貌似可以文件读取 上传文件里面可以上传文件。 先看一下可不可以文件读取 /etc/passwd不能读取&#xff0c;源码提示flag在f1ag.php 看看能不能读取当前的文件&#xff0c; 先把代码摘下来 file.php …...

编程日记 2024/1/29 1:43:00

api管理工具的新发现

一、之前用过的api管理工具 关于api管理工具&#xff0c;之前用过yapi和postman&#xff0c;但是后来发现了这两个工具 二、新发现的更强大的&#xff1a;Apifox和Eolink Apifox和Eolink&#xff0c;那这两个工具有什么优势呢&#xff1f; 2.1Apifox 其中 Apifox Postman …...

编程日记 2024/1/29 1:39:57

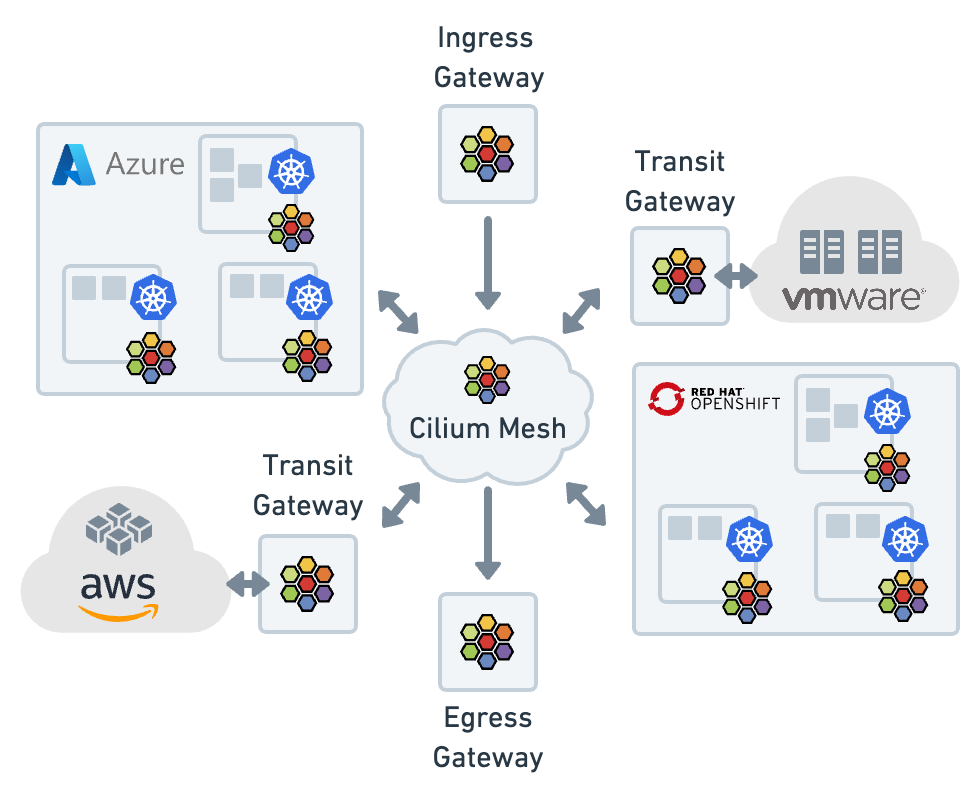
2024 年 eBPF 和网络趋势预测

本文地址&#xff1a;2024 年 eBPF 和网络趋势预测 | 深入浅出 eBPF 1. eBPF 1.1 eBPF 将继续呈指数增长1.2 eBPF 应用市场1.3 eBPF 在手机中得到更广泛的应用1.4 eBPF 滥用带来的风险2. 可观测 2.1 最受欢迎的可观测性2.2 降低可观测性开销2.3 上下文感知的 Kubernetes 工作负…...

编程日记 2024/1/29 1:36:54

2024.1.27 GNSS 学习笔记

1.精确的描述轨道的一组数据(星历)是实现精确定位与导航的基础。 2.GNSS卫星广播星历的提供方式一般有两种&#xff1a;一种是提供开普勒轨道参数和必要的轨道摄动改正项参数&#xff0c;如GPS、BDS、Galileo三大系统采用此种模式&#xff0c;还有QZSS系统&#xff1b;另一种是…...

编程日记 2024/1/29 1:35:53

Unity - 将项目转为HDRP

Camera window -> Package Manager 之后会出现HDRP向导窗口&#xff0c;均点击修复。 在Edit中&#xff0c;更改项目中的材质...

编程日记 2024/1/29 1:33:51

ETCD高可用架构涉及常用功能整理

ETCD高可用架构涉及常用功能整理 1. etcd的高可用系统架构和相关组件1.1 Quorum机制1.2 Raft协议 2. etcd的核心参数2.1 常规配置2.2 特殊优化配置2.2.1 强行拉起新集群 --force-new-cluster2.2.2 兼容磁盘io性能差2.2.3 etcd存储quota 3. etcd常用命令3.1 常用基础命令3.1.1 列…...

编程日记 2024/1/29 1:31:47

利用最小二乘法找圆心和半径

#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

编程新知 2026/1/11 16:05:53

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】

微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来&#xff0c;Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

编程新知 2026/1/11 13:03:58

从深圳崛起的“机器之眼”：赴港乐动机器人的万亿赛道赶考路

进入2025年以来&#xff0c;尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断&#xff0c;但全球市场热度依然高涨&#xff0c;入局者持续增加。 以国内市场为例&#xff0c;天眼查专业版数据显示&#xff0c;截至5月底&#xff0c;我国现存在业、存续状态的机器人相关企…...

编程新知 2026/1/5 23:06:34

【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张（Windows/Linux）

要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况&#xff0c;可以通过以下几种方式模拟或触发&#xff1a; 1. 增加CPU负载 运行大量计算密集型任务&#xff0c;例如&#xff1a; 使用多线程循环执行复杂计算&#xff08;如数学运算、加密解密等&#xff09;。运行图…...

编程新知 2025/11/30 10:30:15

Android15默认授权浮窗权限

我们经常有那种需求&#xff0c;客户需要定制的apk集成在ROM中&#xff0c;并且默认授予其【显示在其他应用的上层】权限&#xff0c;也就是我们常说的浮窗权限&#xff0c;那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

编程新知 2026/1/3 20:12:35

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统

目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索&#xff08;基于物理空间 广播范围&#xff09;2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

编程新知 2025/12/12 6:01:17

Mobile ALOHA全身模仿学习

一、题目 Mobile ALOHA&#xff1a;通过低成本全身远程操作学习双手移动操作 传统模仿学习&#xff08;Imitation Learning&#xff09;缺点&#xff1a;聚焦与桌面操作&#xff0c;缺乏通用任务所需的移动性和灵活性 本论文优点&#xff1a;&#xff08;1&#xff09;在ALOHA…...

编程新知 2026/1/9 15:07:23

Docker 本地安装 mysql 数据库

Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker &#xff1b;并安装。 基础操作不再赘述。 打开 macOS 终端&#xff0c;开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

编程新知 2026/1/10 8:50:43

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体&#xff08;对象或容器&#xff09;QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质&#xff08;定义颜色、反光等&#xff09;QFirstPersonC…...

编程新知 2025/12/20 22:25:49

华为OD机考-机房布局

import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

编程新知 2026/1/2 6:31:25