java的Object类的hasCode()和ToString()
(1)hasCode解释
-
hashCode()是Object类中定义的方法,用于返回对象的哈希码值。哈希码值是一个整数,用于在哈希表等数据结构中快速定位对象。
在Java中,哈希码值的计算是基于对象的内存地址的。默认情况下,hashCode()方法返回的是对象的内存地址的整数表示。因此,对于不同的对象,它们的哈希码值通常是不同的。
hashCode()方法在以下情况下非常有用:
-
哈希表:哈希表是一种常用的数据结构,用于存储和查找键值对。在哈希表中,对象的哈希码值被用作索引,可以快速定位到对应的存储位置。
-
集合类:在Java的集合类中,如HashSet、HashMap等,对象的哈希码值被用于判断对象是否已经存在于集合中。当我们向集合中添加元素时,集合会先计算元素的哈希码值,然后根据哈希码值判断是否存在相同的元素。
需要注意的是,hashCode()方法的实现需要满足以下几个原则:
-
一致性:在对象没有被修改的情况下,多次调用hashCode()方法应该返回相同的结果。
-
相等性:如果两个对象通过equals()方法比较相等,那么它们的hashCode()方法应该返回相同的结果。
-
散列性:不同的对象应该尽可能地产生不同的哈希码值,以减少哈希冲突的概率。
在自定义的类中,如果重写了equals()方法,通常也需要重写hashCode()方法,以保证相等的对象具有相同的哈希码值。重写hashCode()方法时,可以根据对象的内容来计算哈希码值,以实现更精确的哈希码计算。
总结:hashCode()方法是Object类中定义的方法,用于返回对象的哈希码值。哈希码值在哈希表和集合类中起到重要的作用,它可以快速定位对象和判断对象的相等性。在自定义的类中,通常需要重写hashCode()方法,以满足一致性、相等性和散列性的要求。
-
(2)
-
提高局具有哈希结构的容器效率;
-
两个引用,如果指向的是同一个对象,则哈希值肯定是一样的;
-
两个引用,如果指向的是不同的对象,则哈希值不同;
-
哈希值主要是根据地址号得来的,不能完全将哈希值等价于地址;
(3)ToString()
toString()是Object类中定义的方法,用于返回对象的字符串表示。默认情况下,toString()方法返回的是对象的类名和哈希码值的组合,例如"ClassName@hashCode"。但在实际开发中,我们通常会在自定义的类中重写toString()方法,以返回自定义的字符串表示。
重写toString()方法的目的是为了方便调试和输出对象的信息。通过重写toString()方法,我们可以将对象的属性和状态以字符串的形式展示出来,便于程序员理解和调试代码。
以下是重写toString()方法的一般步骤:
-
在类中添加toString()方法的声明,方法的返回类型为String。
-
在toString()方法中,将对象的属性和状态以字符串的形式拼接起来。
-
返回拼接好的字符串。
-
快捷键:alt+insert->ToString();
-
当直接输出一个对象时,toString 方法会被默认的调用;
总结:toString()方法是Object类中定义的方法,用于返回对象的字符串表示。通过重写toString()方法,我们可以自定义对象的字符串表示,方便调试和输出对象的信息。重写toString()方法的一般步骤是将对象的属性和状态以字符串的形式拼接起来,并返回拼接好的字符串。
相关文章:
和ToString())
java的Object类的hasCode()和ToString()
(1)hasCode解释 hashCode()是Object类中定义的方法,用于返回对象的哈希码值。哈希码值是一个整数,用于在哈希表等数据结构中快速定位对象。 在Java中,哈希码值的计算是基于对象的内存地址的。默认情况下,ha…...
判断一维数组和多元数组中的元素是否相等并输出键值key)
php数组算法(1)判断一维数组和多元数组中的元素是否相等并输出键值key
在php中,如何判断[1,0,1]和[ [0, 0, 0],//体质正常 [1, 0, 0],//气虚体质 [0, 1, 0],//血瘀体质 [0, 0, 1],//阴虚体质 [1, 1, 0],//气虚兼血瘀体质 [1, 0, 1],//气虚兼阴虚体质 [0, 1, 1],//血瘀兼阴虚体质 [1, 1, 1],//气虚兼血瘀兼阴虚体质 ];中的第n项相等&…...

已解决Error:AttributeError: module ‘numpy‘ has no attribute ‘float‘.
成功解决Error:AttributeError: module ‘numpy‘ has no attribute ‘float‘. 🌵文章目录🌵 🌳引言🌳🌳报错分析🌳🌳解决方案1:降低NumPy版本🌳ἳ…...

WordPress块编辑器(Gutenberg古腾堡)中如何添加脚注?
WordPress默认自带的块编辑器(Gutenberg古腾堡编辑器)本身就自带添加脚注功能,不过经典编辑器不行。如果想要在WordPress中添加更加专业的脚注,建议使用Modern Footnotes插件,具体介绍及使用请参考『WordPress站点如…...
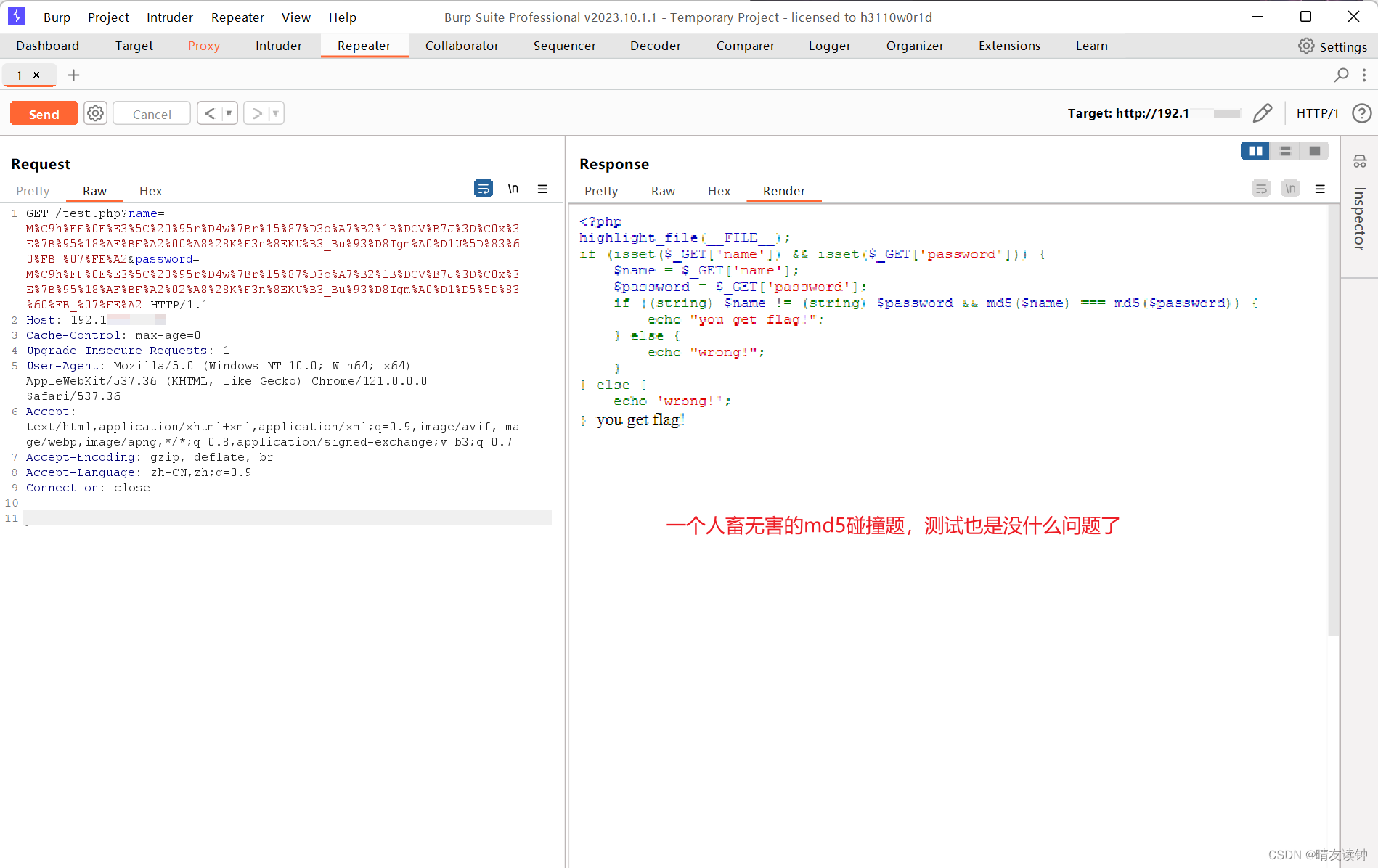
burpsuite怎么进行本地抓包?ctfer测试自搭建靶场必须学会!
自己搭建靶场测试题目是ctfer不可避免的环节,怎么用burp对本地回环即localhost进行抓包?笔者在本篇分享一下自己的解决经验。 笔者用的是Chrome浏览器,如果是火狐浏览器可以参考本篇:Burp Suite抓不到本地包/localhost包问题解决…...

VSCode Python调试运行:json编写
对于需要在命令行传参运行的项目,如果想要调试运行,则需要编写对应的launch.json文件这里记录一下json文件的编写格式: {"version": "0.2.0","configurations": [{"python": "/data/xxx/minic…...
自动化Web页面性能测试介绍
随着越来越多的用户使用移动设备访问 Web 应用,使得 Web 应用需要支持一些性能并不是很好的移动设备。为了度量和测试 Web 应用是不是在高复杂度的情况下,页面性能能满足用户的需求。 同时,随着 Web 应用的空前发展,前端业务逐渐…...
可视化 | 【d3】力导向关系图优化(搜索+刷新)
文章目录 📚优化内容📚html和css优化🐇搜索框部分🐇刷新按钮部分 📚js🐇搜索框部分🐇刷新部分 前期回顾:【d3】力导图优化,本文主要是基于上篇代码,以代码段添…...

2024.1.26力扣每日一题——计算 K 置位下标对应元素的和
2024.1.26 题目来源我的题解方法一 位运算统计二进制数中1的个数方法二 官方的一种优化计算二进制中1的个数的方法 题目来源 力扣每日一题;题序:2859 我的题解 方法一 位运算统计二进制数中1的个数 对于每一个位置i都去计算i对应的二进制数中1的个数 …...
:获取或设置分类等级列表)
R语言【taxlist】——levels():获取或设置分类等级列表
Package taxlist version 0.2.4 Description 分类层次结构可以设置为 taxlist 对象中的级别,按从低到高的顺序排列。 在 taxlist 对象中为特定分类概念添加分类级别。此外,概念限制的变化可能涉及其分类层次结构的变化。 Usage levels(x)## S3 method…...

单元测试——题目十三
目录 题目要求: 定义类 测试类 题目要求: 根据输入的三条边值判断能组成何种三角形。三条边为变量a、b、c,范围为1≤边值≤10,不在范围内,提示“输入边值不在范围内”。不满足任意两边之和必须大于第三边,提示“输入边值不能组成三角形”。输入边值能组成三角形,只有…...
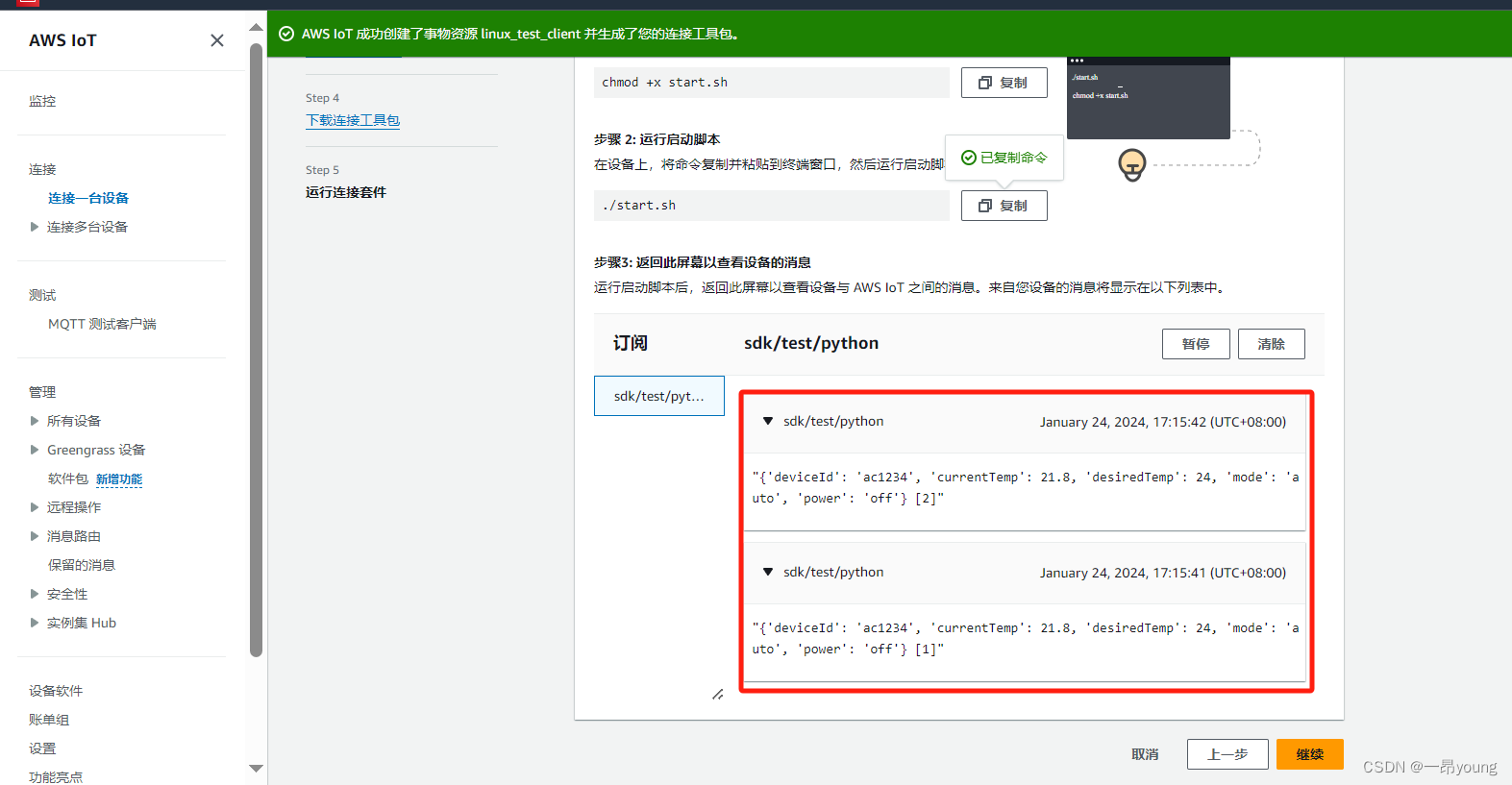
使用Linux SDK客户端向AWS Iot发送数据
参考链接: https://ap-southeast-1.console.aws.amazon.com/iot/home?regionap-southeast-1#/test 此篇文章用于测试,使用Linux SDK客户端向AWS Iot发送数据,准备环境如下: 1、客户端环境准备 1.1 客户端操作系统 虚拟机一台…...

1.27学习总结
今天做了些队列的题: 1.逛画展(单调队列) 2.打印队列 Printer Queue(优先队列) 3.[NOIP2010 提高组] 机器翻译(模拟队列) 4.求m区间内的最小值(单调队列板子题) 5.日志统计(滑动窗口,双指针) 总结一下&…...

【算法专题】二分查找(进阶)
📑前言 本文主要是二分查找(进阶)的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 🌄每日…...

开源项目对于新用户和初学者适合哪些工作
目录 一、阅读和理解文档 二、报告问题 三、测试和验证修复 四、编写和更新文档 五、简单的代码更改和修复 六、参与社区讨论 开源项目对于新用户和初学者来说,提供了宝贵的学习和实践机会。以下是一些适合新用户和初学者参与的工作: 一、阅读和理…...

linux中配置文件目录为什么用etc来命名
在早期的 Unix 系统中,/etc 目录的名称确实来源于单词 “etcetera” 的缩写,最初意味着 “其他”,用来存放杂项或者不属于其他特定目录的文件。然而,随着时间的推移,/etc 目录的用途逐渐演变并专门化。 在现代的 Linux…...
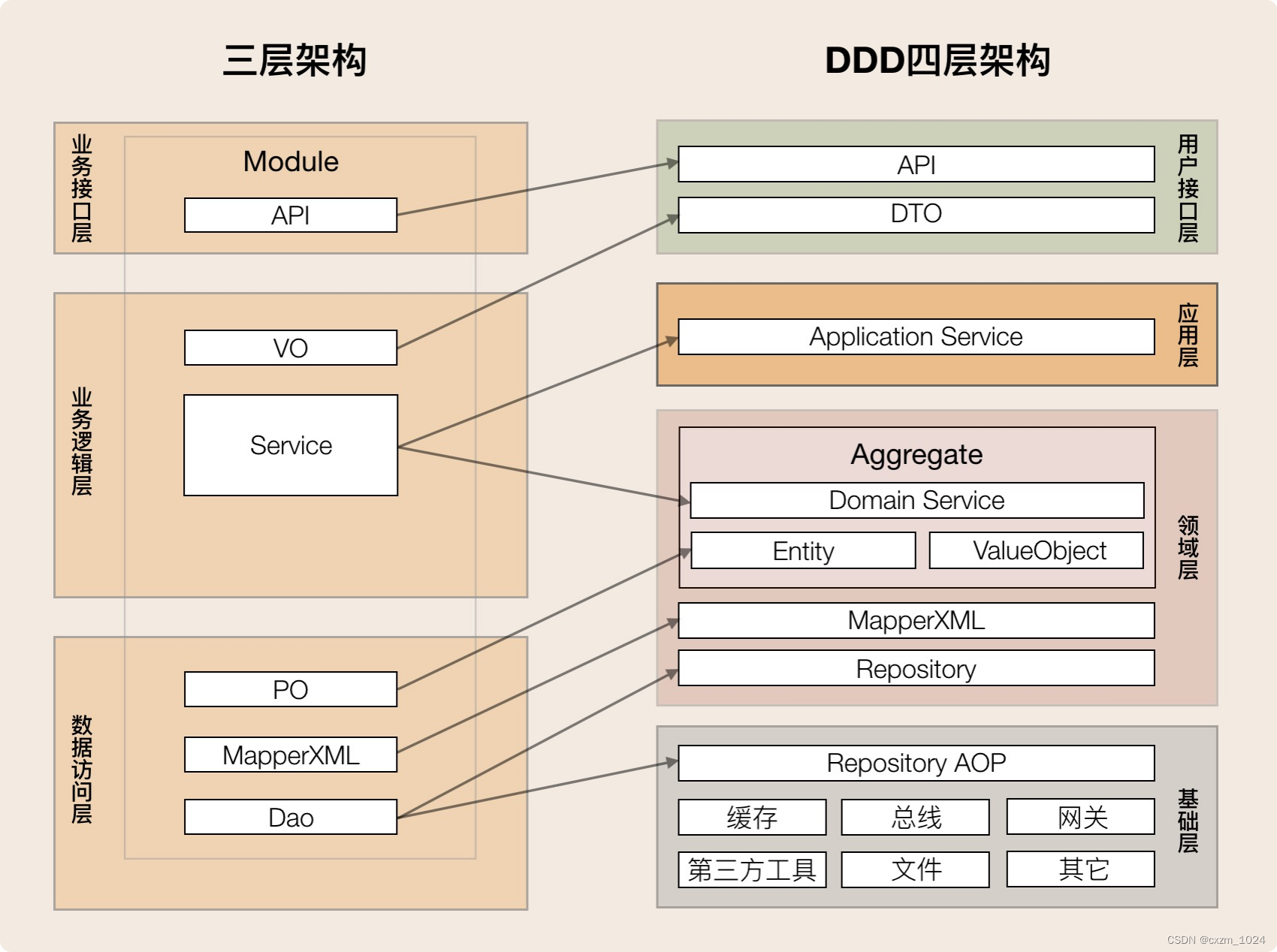
06.领域驱动设计:使用DDD分层架构,可以有效降低层与层之间的依赖
目录 1、概述 2、什么是DDD分层架构 1.用户接口层 2.应用层 3.领域层 4.基础层 3、DDD分层架构最重要的原则是什么 4、DDD分层架构如何推动架构演进 1.微服务架构的演进 2.微服务内服务的演进 5、三层架构如何演进到DDD分层架构 我们该怎样转向DDD分层架构 6、总结…...

HCIA-Datacom实验指导手册:3.2 实验二:生成树基础实验
HCIA-Datacom实验指导手册:3.2 实验二:生成树基础实验 一、实验介绍:二、实验拓扑:三、实验目的:四、配置步骤:步骤 1 掌握启用和禁用 STP/RSTP 的方法步骤 2 掌握修改交换机 STP 模式的方法步骤 3 掌握修改桥优先级,控制根桥选举的方法步骤 4 掌握修改端口优先级,控制…...

WPF的ViewBox控件
在WPF中,ViewBox是一个用于缩放和调整其子元素大小的容器控件。它可以根据可用空间自动调整子元素的大小,以使其适应ViewBox的边界。这使得在不同尺寸的窗口或布局中保持元素的比例和缩放变得更加容易。 ViewBox具有以下重要属性: Stretch&…...
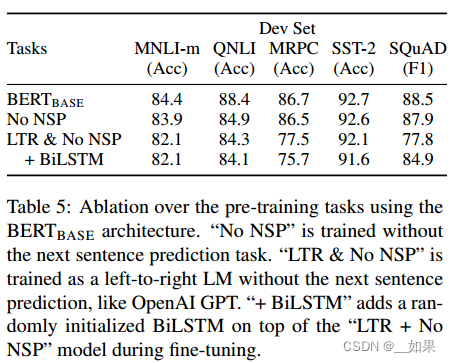
论文精读--BERT
不像视觉领域,在Bert出现之前的nlp领域还没有一个深的网络,使得能在大数据集上训练一个深的神经网络,并应用到很多nlp的任务上 Abstract We introduce a new language representation model called BERT, which stands for Bidirectional En…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
