【数据分析】numpy基础第五天
文章目录
- 前言
- Z-Score标准化
- Z-Score应用示例
- Min-Max归一化
- Min-Max应用示例
- 总结
前言
第五天是我们的numpy学习计划中的最后一天。
在数据处理和数据分析中,数据预处理是非常重要的一步。我们不可能完全靠肉眼来分析数据,总会有用到各种算法模型的时候,例如使用聚类、回归分析。
如果原来的数据非常“肮脏”,不规整,我们将会得到一个不可靠的糟糕结果,此时我们需要用两种十分常用的数据预处理手段来清洗我们的数据。
今天仅仅包括如下两个内容:
- Z-Score标准化
- Min-Max归一化
Z-Score标准化
Z-Score标准化是一种常见的数据标准化方法,它通过对原始数据进行均值和标准差的线性变换,将数据变换为均值为0、标准差为1的分布。
Z-Score标准化后的数据,通常在机器学习模型上表现更好,并且,我们可以根据Z-Score标准化后的数据来去除异常值。
具体的标准化公式如下:
X standardized = X − X ˉ σ X_{\text{standardized}} = \frac{{X - \bar{X}}}{{\sigma}} Xstandardized=σX−Xˉ
其中, X s t a n d a r d i z e d X_{standardized} Xstandardized表示标准化后的数据, X X X表示原始数据, X m e a n X_{mean} Xmean表示原始数据的均值, X s t d X_{std} Xstd表示原始数据的标准差。
关于Z分数(Z-Score):
其实Z-Score标准化,就是数据计算成对应的Z分数,我们可以利用Z分数进行异常值处理,如果Z分数大于某一个阈值(通常 ± 2),则认为它是异常值,进行丢弃。
使用Z分数处理异常值需要满足正态分布的假设。Z分数越大,就代表它越接近正态分布的右侧,Z分数越小,就代表它越接近正态分布的左侧,对于那些及其右侧或者及其左侧的数据,因为很可能是错误的数据,所以视为异常值。
Z = X − X ˉ σ Z = \frac{{X - \bar{X}}}{{\sigma}} Z=σX−Xˉ
下面是使用Numpy实现Z-Score标准化的代码示例:
import numpy as npdef z_score(X):X_mean = np.mean(X)X_std = np.std(X)X_standardized = (X - X_mean) / X_stdreturn X_standardizedZ-Score应用示例
在运行过上面的Z-Score标准化的实现代码后,我们可以运行下面的代码。
假设我们现在有一批大学生的身高数据:
- 我们知道,正常成年人的身高一般都是在
[150, 190]之间 - 而我们在下面的数据中添加了一个身高为
300的异常数据
让我们来看看它的Z分数是多少,并找出300这个异常身高。
# 身高数据
arr = np.array([160, 170, 180, 165, 155, 163, 183, 188, 300])# 计算arr中的元素的z分数
std_data = z_score(arr)# np.abs()可以计算绝对值
abs_zc = np.abs(std_data)print('原数据:')
print(arr)
print()print('Z分数的绝对值:')
print(abs_zc)
print()# 大于号“>”也是一个运算符,运算结果是True和False
compare = abs_zc > 2
print('比较结果:')
print(compare)
print()# compare和arr的形状相同,区别是arr里面的是真正的数据,compare对应每个元素的比较结果
# 只有对应在compare里面为True的元素会被筛选出来
outlier = arr[compare]print('异常值:')
print(outlier)输出结果
从下面的输出结果中,我们可以看到,正常的身高的Z分数的绝对值都位于[0, 1]之间,而身高为300的那个异常数据的Z分数为2.73893945,显然,这已经远远大于了2这个阈值(这个阈值的设定并没有严格限定,我只能告诉你,阈值的绝对值越高,去除的数据越少,反之越多,这对应了正态分布的左右两端都只有少量数据的特点,通过设定Z分数的阈值,我们只保留正态分布中间的那些常见数据),我们应该将它视为异常值去除。
原数据:
[160 170 180 165 155 163 183 188 300]Z分数的绝对值:
[0.59220312 0.35426437 0.11632561 0.47323375 0.7111725 0.52082150.04494399 0.07402539 2.73893945]比较结果:
[False False False False False False False False True]异常值:
[300]Min-Max归一化
Min-Max归一化是一种线性变换方法,将数据缩放到指定的范围内。它通过对原始数据进行线性变换,将数据映射到[0, 1]的范围内。
有时候原始数据的尺度相差太大,不满足我们的算法模型的假设(假设不同数据的尺度都是一致的),可能会让我们得到了错误的结果,此时我们就应该使用Min-Max归一化,将数据归一化到[0, 1]之间。
具体的归一化公式如下:
X normalized = X − X min X max − X min X_{\text{normalized}} = \frac{{X - X_{\text{min}}}}{{X_{\text{max}} - X_{\text{min}}}} Xnormalized=Xmax−XminX−Xmin
其中, X n o r m a l i z e d X_{normalized} Xnormalized表示归一化后的数据, X X X表示原始数据, X m i n X_{min} Xmin表示原始数据的最小值, X m a x X_{max} Xmax表示原始数据的最大值。
下面是使用Numpy实现Min-Max归一化的代码示例:
import numpy as npdef min_max(X):X_min = np.min(X)X_max = np.max(X)X_normalized = (X - X_min) / (X_max - X_min)return X_normalized
关于Min-Max其它小内容
其实不一定是归一化到[0, 1]这个区间中,有些特殊情况会需要归一化到[-1, 1]或者别的区间,但是大部分时候都是[0, 1]区间。
Min-Max应用示例
在运行过上面的Min-Max归一化的实现代码后,我们可以运行下面的代码。
假设我们现在有两批医学数据:
大尺度的是患者平均的每日步数小尺度的是患者的体脂百分比。
这两批数据的尺度非常巨大,如果算法模型更偏向大数值的数据,那么毫无疑问会偏向患者的平均每日步数这一边,这并不是我们想要的结果,因此我们需要进行Min-Max归一化。
具体看下面的代码:
# 创建两列尺度差距很大的数据
col1 = np.array([55000, 45000, 35000, 25000, 15000]) # 较大数值的数据列
col2 = np.array([15, 25, 35, 45, 55]) # 较小数值的数据列# 分别应用Min-Max规约
normalized_col1 = min_max(col1)
normalized_col2 = min_max(col2)# 输出原始数据和归一化后的数据
print("原始数据 - 较大数值的列:")
print(col1)
# \n 代表换行符,仅仅写print()的时候,输出的就是\n这个换行符
print("\n归一化后 - 较大数值的列:")
print(normalized_col1)print("\n原始数据 - 较小数值的列:")
print(col2)
print("\n归一化后 - 较小数值的列:")
print(normalized_col2)
总结
本文介绍了使用Numpy实现Min-Max归一化和Z-Score标准化算法的方法。归一化和标准化是数据预处理中常用的技术,能够有效地提高数据的可处理性和模型的性能。在实际应用中,根据具体的数据情况选择合适的预处理方法是非常重要的。希望本文能对读者在使用Numpy进行数据预处理时有所帮助。
相关文章:

【数据分析】numpy基础第五天
文章目录 前言Z-Score标准化Z-Score应用示例 Min-Max归一化Min-Max应用示例 总结 前言 第五天是我们的numpy学习计划中的最后一天。 在数据处理和数据分析中,数据预处理是非常重要的一步。我们不可能完全靠肉眼来分析数据,总会有用到各种算法模型的时候…...

CSS 双色拼接按钮效果
<template><view class="sss"><button> <!-- 按钮 --><view class="span"> 按钮 </view> <!-- 按钮文本 --></button></view></template><script></script><style>body {b…...
T05垃圾收集算法与垃圾收集器ParNew CMS
垃圾收集算法与垃圾收集器ParNew & CMS 垃圾收集算法 #### f 分代收集理论 当前虚拟机的垃圾收集都采用分代收集算法。根据对象存活周期不同将内存分为几块,一般将java堆分为新生代和老年代,然后根据各个年代的特点选择不同的垃圾收集算法。 在新…...

每日一道面试题:Java中序列化与反序列化
写在开头 哈喽大家好,在高铁上码字的感觉是真不爽啊,小桌板又拥挤,旁边的小朋友也比较的吵闹,影响思绪,但这丝毫不影响咱学习的劲头!哈哈哈,在这喧哗的车厢中,思考着这样的一个问题…...

论文阅读:Vary-toy论文阅读笔记
目录 引言整体结构图方法介绍训练vision vocabulary阶段PDF数据目标检测数据 训练Vary-toy阶段Vary-toy结构数据集情况 引言 论文:Small Language Model Meets with Reinforced Vision Vocabulary Paper | Github | Demo 说来也巧,之前在写论文阅读&…...
【Linux】开始使用 vim 吧!!!
Linux 1 what is vim ?2 vim基本概念3 vim的基本操作 !3.1 vim的快捷方式3.1.1 复制与粘贴3.1.2 撤销与剪切3.1.3 字符操作 3.2 vim的光标操作3.3 vim的文件操作 总结Thanks♪(・ω・)ノ感谢阅读下一篇文章见!…...

多线程面试合集
前言 前文介绍了JVM相关知识,本文将重点介绍多线程相关知识以及工作中的一些经验。 多线程面试合集 什么是多线程?为什么我们需要多线程? 多线程是指在一个进程中同时执行多个线程,每个线程可以执行不同的任务。多线程可以提高…...

从微服务到云原生
很多文章介绍云原生概念,说它包含微服务,又包含了其它几个方面的东西,还扯到文化层面、组织层面和技术层面,搞技术的人一听到公司文化问题和组织部门问题,就十分地晕眩,不能让我好好地坐下来写写代码、搞搞…...
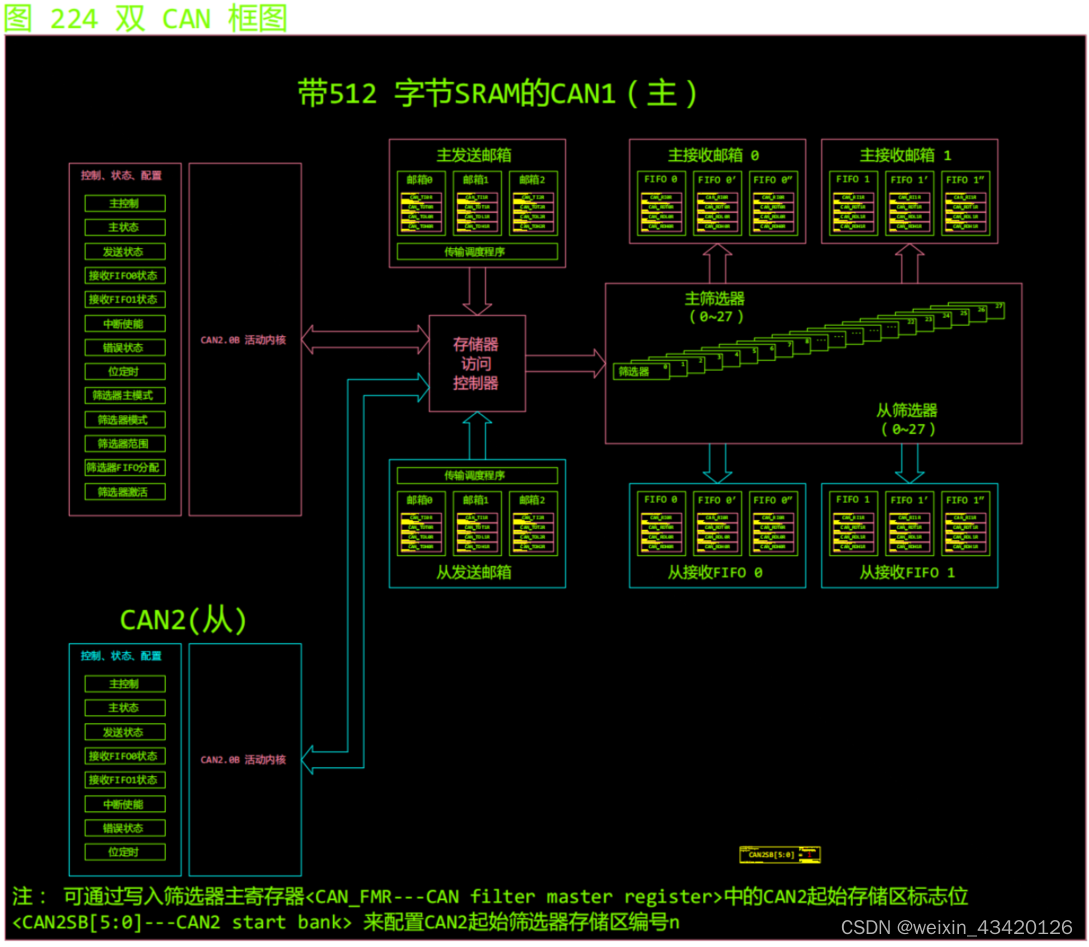
bxCAN 主要特性
bxCAN 主要特性 ● 支持 2.0 A 及 2.0 B Active 版本 CAN 协议 ● 比特率高达 1 Mb/s ● 支持时间触发通信方案 发送 ● 三个发送邮箱 ● 可配置的发送优先级 ● SOF 发送时间戳 接收 ● 两个具有三级深度的接收 FIFO ● 可调整的筛选器组: — CAN1 和…...

武忠祥2025高等数学,基础阶段的百度网盘+视频及PDF
考研数学武忠祥基础主要学习以下几个方面的内容: 1.微积分:主要包括极限、连续、导数、积分等概念,以及它们的基本性质和运算方法。 2.线性代数:主要包括向量、向量空间、线性方程组、矩阵、行列式、特征值和特征向量等概念,以及它们的基本…...
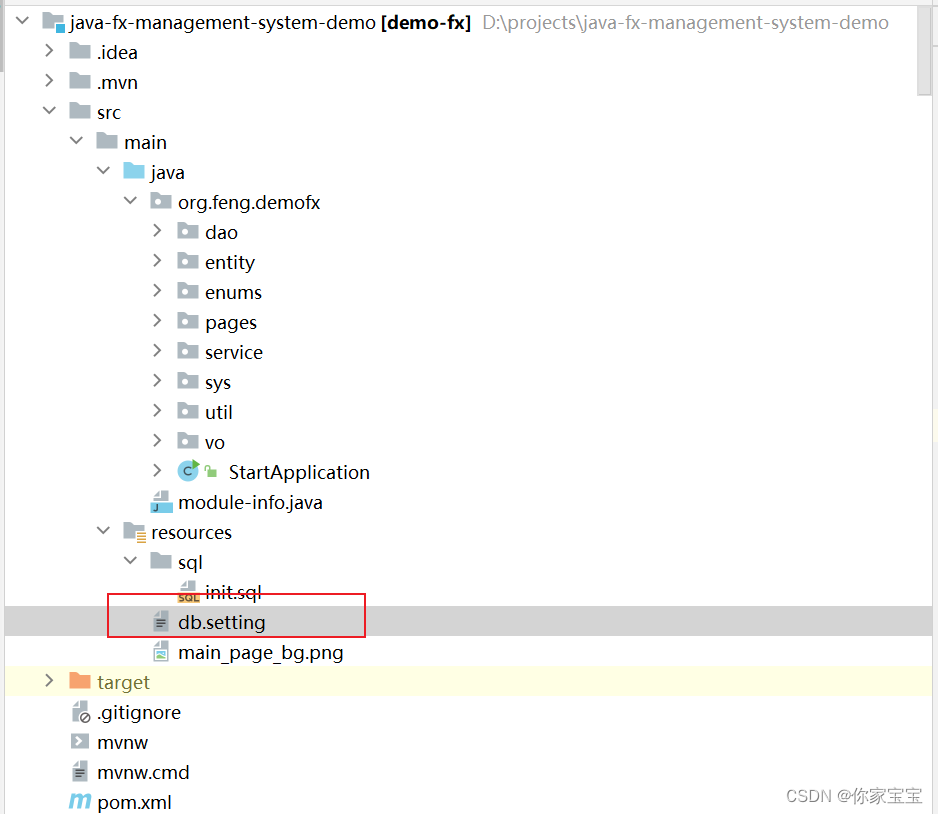
用JavaFX写了一个简易的管理系统
文章目录 前言正文一、最终效果1.1 主页面1.2 动物管理页面-初始化1.3 动物管理页面-修改&新增1.4 动物管理页面-删除&批量删除 二、核心代码展示2.1 启动类2.2 数据库配置-db.setting2.3 日志文本域组件2.4 自定义表格视图组件2.5 自定义分页组件2.6 动物管理页面2.7 …...

第二百九十回
文章目录 1. 概念介绍2. 方法与细节2.1 实现方法2.2 具体细节 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何混合选择多个图片和视频文件"相关的内容,本章回中将介绍如何通过相机获取视频文件.闲话休提,让我们一起Talk Flutter吧。 1. …...
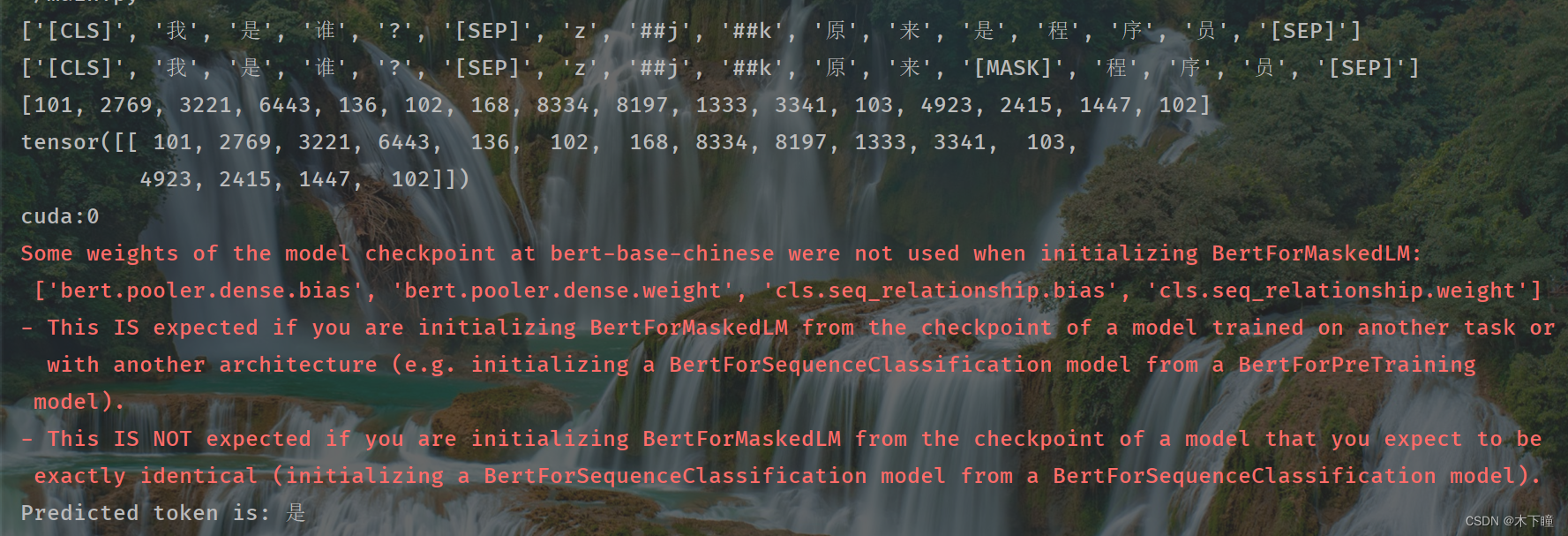
bert实现完形填空简单案例
使用 bert 来实现一个完形填空的案例,使用预训练模型 bert-base-chinese ,这个模型下载到跟代码同目录下即可,下载可参考:bert预训练模型下载-CSDN博客 通过这个案例来了解一下怎么使用预训练模型来完成下游任务,算是对…...
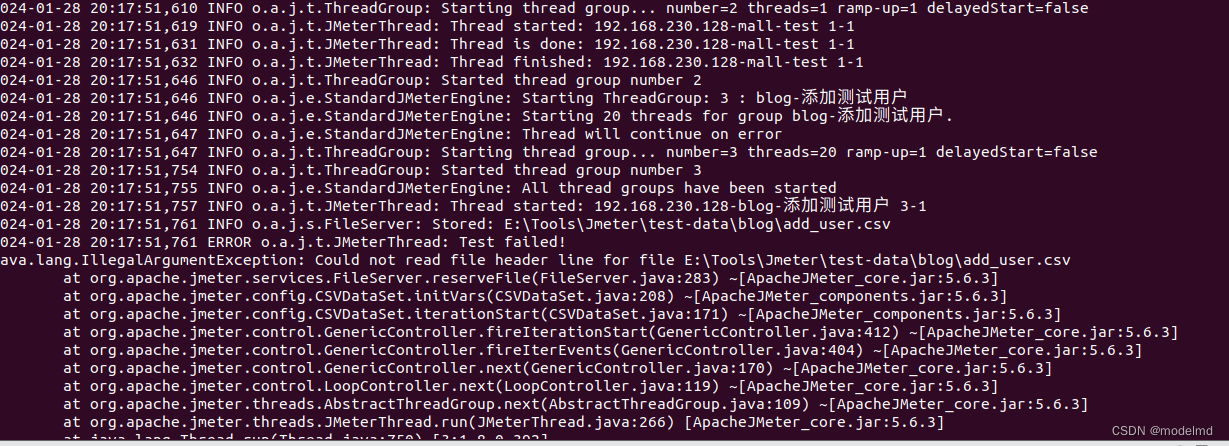
Jmeter 分布式测试
Jmeter单机进行压测,受到单台机器的性能影响,Jmeter支持分布式测试,用一个控制节点去控制多个工作节点去模拟更多的用户。 版本信息 内容版本号JDK1.8Jmeter5.6.2 分布式测试原理 jmeter 官网对分布式测试有说明,jmeter分布式…...

在 Ubuntu 上安装 Docker Engine
系列文章目录 前言 要在 Ubuntu 上开始使用 Docker Engine,请确保满足先决条件,然后按照安装步骤进行操作。 一、先决条件 注意事项 如果您使用 ufw 或 firewalld 管理防火墙设置,请注意当您使用 Docker 暴露容器端口时,这些端口…...

Mac安装nvm,安装多个不同版本node,指定node版本
一.安装nvm brew install nvm二。配置文件 touch ~/.zshrc echo export NVM_DIR~/.nvm >> ~/.zshrc echo source $(brew --prefix nvm)/nvm.sh >> ~/.zshrc三.查看安装版本 nvm -vnvm常用命令如下:nvm ls :列出所有已安装的 node 版本nvm…...

【开源】基于JAVA+Vue+SpringBoot的智慧家政系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、系统展示四、核心代码4.1 查询家政服务4.2 新增单条服务订单4.3 新增留言反馈4.4 小程序登录4.5 小程序数据展示 五、免责说明 一、摘要 1.1 项目介绍 基于微信小程序JAVAVueSpringBootMySQL的智慧家政系统࿰…...

Python NLP深度学习进阶:自然语言处理
自然语言处理(Natural Language Processing,NLP)是人工智能领域中的一个重要分支,涉及到处理和理解人类语言的方法和技术。随着深度学习的快速发展,NLP的研究和应用也在不断进步。 在Python中,有许多强大的…...
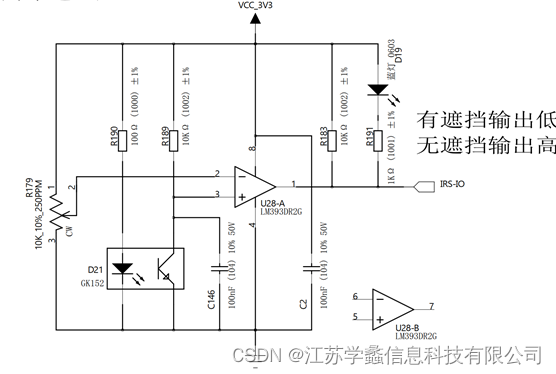
STM32单片机基本原理与应用(三)
矩阵键盘工作原理 矩阵键盘由多个独立按键组成,按键的一端接地,一端接MCU的GPIO。当按键没有被按下时,电路其实是一个断路,将单片机该引脚设置成输入上拉状态,读到的电平为高电平。当按下按键时,引脚会被拉…...

Android studio布局详解
文章目录 一、Android studio布局详解二、Android studio六大布局案例三、优缺点四、热门文章 一、Android studio布局详解 Android Studio是一种用于开发Android应用程序的集成开发环境(IDE),用于设计和编辑Android应用程序的用户界面布局。在Android …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...
