SS-ELM-AE与S2-BLS相关论文阅读记录
Broad learning system for semi-supervised learning
摘要:本文认为,原始BLS采用的稀疏自编码器来生成特征节点是一种无监督学习方法,这意味着忽略了标注数据的一些信息,并且难以保证同类样本之间的相似性和相邻性,同时SS-BLS和BLS都是构造线性模型,当不同类的样本分布存在重叠时,难以取得良好的分类效果。因此本文提出了一种新的半监督BLS——S2-BLS。
SS-ELM-AE
本文认为,SS-BLS或者是SS-ELM在引入非监督信息,即流形化的时候,考虑到选取k近邻点的情况,但是这种方法可能存在的缺点就是如果大多数标注样本它们所选择的k个近邻点都是标注样本,然后大多数无标注样本所选择的k个近邻点都是无标注样本,那么就没有充分利用到标注样本和未标注样本之间的关系。因此将SS-ELM-AE的目标函数定义为:
LSS−ELM−AE=12∥HW−X∥F2+C2∥W∥F2+λ2(GLL+GLU)L_{SS-ELM-AE}=\frac{1}{2}\Vert HW-X\Vert^2_F+\frac{C}{2}\Vert W\Vert^2_F+\frac{\lambda}{2}(G_{LL}+G_{LU}) LSS−ELM−AE=21∥HW−X∥F2+2C∥W∥F2+2λ(GLL+GLU)
其中X代表所有样本。而GLL、GLUG_{LL}、G_{LU}GLL、GLU分别代表标注样本内部之间的信息以及标注样本和无标注样本之间的信息。
对于标注样本,其相似度矩阵定义为:
SijL={1yi,yj∈t0otherwiseS^L_{ij}=\begin{cases}1\quad y_i,y_j \in t\\0\quad otherwise\end{cases} SijL={1yi,yj∈t0otherwise
就是属于同类的相似度为1,否则为0。因此GLLG_{LL}GLL表示为:
GLL=12∑i=1l∑j=1lSijL∥g(xi)−g(xj)∥F2G_{LL}=\frac{1}{2}\sum_{i=1}^l\sum_{j=1}^lS^L_{ij}\Vert g(x_i)-g(x_j)\Vert ^2_F GLL=21i=1∑lj=1∑lSijL∥g(xi)−g(xj)∥F2
其中g(x)g(x)g(x)代表模型对样本的输出。
而对于未标注样本,其相似性矩阵定义为:
SijLU={1xi∈knn(xj),j∗orxj∈knn(xi),i∗0otherwiseS^{LU}_{ij}=\begin{cases}1\quad x_i\in knn(x_j),j^* ~~or ~~x_j\in knn(x_i),i^*\\0\quad otherwise\end{cases} SijLU={1xi∈knn(xj),j∗ or xj∈knn(xi),i∗0otherwise
其中j∗j^*j∗表示如果xjx_jxj是标注样本,那么其k个近邻点要从未标注样本之中选择。因此
GLU=12∑i=1l+u∑j=1l+uSijLU∥g(xi)−g(xj)∥F2G_{LU}=\frac{1}{2}\sum_{i=1}^{l+u}\sum_{j=1}^{l+u}S^{LU}_{ij}\Vert g(x_i)-g(x_j)\Vert ^2_F GLU=21i=1∑l+uj=1∑l+uSijLU∥g(xi)−g(xj)∥F2
那么可以将该矩阵写为:
SLU=(0LLSLUSULSUU)S_{LU}=\left(\begin{matrix}0_{LL}\quad S_{LU}\\S_{UL }\quad S_{UU}\end{matrix}\right) SLU=(0LLSLUSULSUU)
斜对角线两个矩阵应该是转置关系。SUUS_{UU}SUU就是简单的knn来计算。因此有:

其中G=[g(x1);...;g(xl+u)]G=[g(x_1);...;g(x_{l+u})]G=[g(x1);...;g(xl+u)]。L定义为:
L=D−SD=diag(d1,...,dl+u),di=∑i=1l+uSijS=(SLSLUSULSUU)L=D-S\\D=diag(d_1,...,d_{l+u}),d_i=\sum_{i=1}^{l+u}S_{ij}\\S=\left(\begin{matrix}S^L\quad S_{LU}\\S_{UL}\quad S_{UU}\end{matrix}\right) L=D−SD=diag(d1,...,dl+u),di=i=1∑l+uSijS=(SLSLUSULSUU)
因此可以推导出:
LSS−ELM−AE=12∥HW−X∥F2+C2∥W∥F2+λ2Tr(WTHTLHW)L_{SS-ELM-AE}=\frac{1}{2}\Vert HW-X\Vert^2_F+\frac{C}{2}\Vert W\Vert^2_F+\frac{\lambda}{2}Tr(W^TH^TLHW) LSS−ELM−AE=21∥HW−X∥F2+2C∥W∥F2+2λTr(WTHTLHW)
当输出节点输出多于隐藏层节点数目,可解出:

否则:

注意这里的损失函数是重构误差,因此可以看成是一个结合ELM思想的AE,是用来求解输入到隐藏层的权重的,而不是像ELM最终求解隐藏层到输出的权重的。
因此求解输入到特征节点映射的权重过程为:

S2-BLS
该算法就是对原有SS-BLS算法的改良,其利用了同样样本间的相似性和近邻点间的相似性信息来获取映射后的特征,同时考虑了类内紧性和类间可分性,获得更好的判别模型。具体来说:
其特征节点的定义比较特殊,用到了非线性激活函数,即:
Zi=ϕi(XWeiT),i=1,2,...,nZ_i=\phi_{i}(XW^T_{ei}),i=1,2,...,n Zi=ϕi(XWeiT),i=1,2,...,n
其中权重WeiW_{ei}Wei正是通过SS-ELM-AE来获得的,而ϕ\phiϕ是非线性函数。然后狗仔增强节点的过程与普通BLS相同,因此得到P=[Zn∣Hm]P=[Z^n\mid H^m]P=[Zn∣Hm]
那么在计算输出权重时,其考虑了类内紧性和类间可分性,即:

因此构造的损失项为:

其中F=[F1;...;Fl+u]F=[F_1;...;F_{l+u}]F=[F1;...;Fl+u]为对每个样本模型的预测向量,Lintra=Dintra−Sintra=diag(d1intra,...,dl+uintra)L_{intra}=D^{intra}-S_{intra}=diag(d^{intra}_1,...,d^{intra}_{l+u})Lintra=Dintra−Sintra=diag(d1intra,...,dl+uintra),diintra=∑i=1l+uSintraijd^{intra}_i=\sum_{i=1}^{l+u}S^{ij}_{intra}diintra=∑i=1l+uSintraij。

其中LinterL_{inter}Linter也类似。
那么结合这两个L矩阵,可以用参数进行衡量。因此目标函数为:

其中
U=(Ul×l,000)Ul×l=diag(1,...,1)F=Pβ,β为连接权重L~=ηLintra−(1−η)LinterU=\left(\begin{matrix}U_{l\times l},\quad 0\\~~~0\quad ~~~~0\end{matrix}\right)\\U_{l\times l}=diag(1,...,1)\\F=P\beta, ~~~~\beta 为连接权重\\\tilde{L}=\eta L_{intra}-(1-\eta)L_{inter} U=(Ul×l,0 0 0)Ul×l=diag(1,...,1)F=Pβ, β为连接权重L~=ηLintra−(1−η)Linter
当样本数目多于隐藏层节点数目,可解出

否则:

其示意图大致如下所示:

伪代码如下所示:

总结
这篇文章从两部分作为创新点,一是原先BLS的AE寻求特征节点映射的部分,这部分它结合了ELM的思想来求解权重向量,第二部分是在求解链接输出的权重时,加入了类内和类间样本之间的关系矩阵。
相关文章:

SS-ELM-AE与S2-BLS相关论文阅读记录
Broad learning system for semi-supervised learning 摘要:本文认为,原始BLS采用的稀疏自编码器来生成特征节点是一种无监督学习方法,这意味着忽略了标注数据的一些信息,并且难以保证同类样本之间的相似性和相邻性,同…...

ESP32设备驱动-MAX6675冷端补偿K热电偶数字转换器
MAX6675冷端补偿K热电偶数字转换器 1、MAX6675介绍 MAX6675执行冷端补偿并将来自K型热电偶的信号数字化。 数据以 12 位分辨率、SPI™ 兼容的只读格式输出。 该转换器可将温度解析为 0.25C,读数高达 +1024C,并且在 0C 至 +700C 的温度范围内具有 8 LSB 的热电偶精度。 MAX…...
)
Python基础知识汇总(字符串四)
目录 字母的大小写转换 lower()方法 upper()方法 删除字符串中的空格和特殊字符 strip()方法...

C语言学习笔记——指针(初阶)
前言 指针可以说是C语言基础语法中最难的理解的知识之一,很多新手(包括我)刚接触指针时都觉得很难。在我之前发布的笔记中都穿插运用了指针,但是我一直没有专门出一期指针的笔记,这是因为我确实还有些细节至今还不太清…...

阿赵的MaxScript学习笔记分享十二《获取和导出各种数据》
大家好,我是阿赵,周日的早上继续分享MaxScript学习笔记,这是第十二篇,获取和导出各种数据 1、导出数据的目的 使用3DsMax建立3D模型后,很多时候需要输出模型到别的引擎去使用,常用的格式有Obj、FBX、SLT等…...

react-draggable实现拖拽详解
react-draggable属性常用属性属性列表事件列表举例首先安装 react-draggable实现移动希望小编写的能够帮助到你😘属性 常用属性 属性默认值介绍axisxhandle拖动的方向,可选值 x ,y,bothhandle无指定拖动handle的classposition无handle的位置࿰…...

01.进程和线程的区别
进程和线程的区别进程和线程是计算机中的两个核心概念,它们都是用来实现并发执行的方式,但是它们在实现并发的方式和资源管理方面有一些重要的区别。进程是一个程序的运行实例。每个进程都有自己的内存空间、代码、数据和系统资源(如文件描述…...

逻辑优化-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
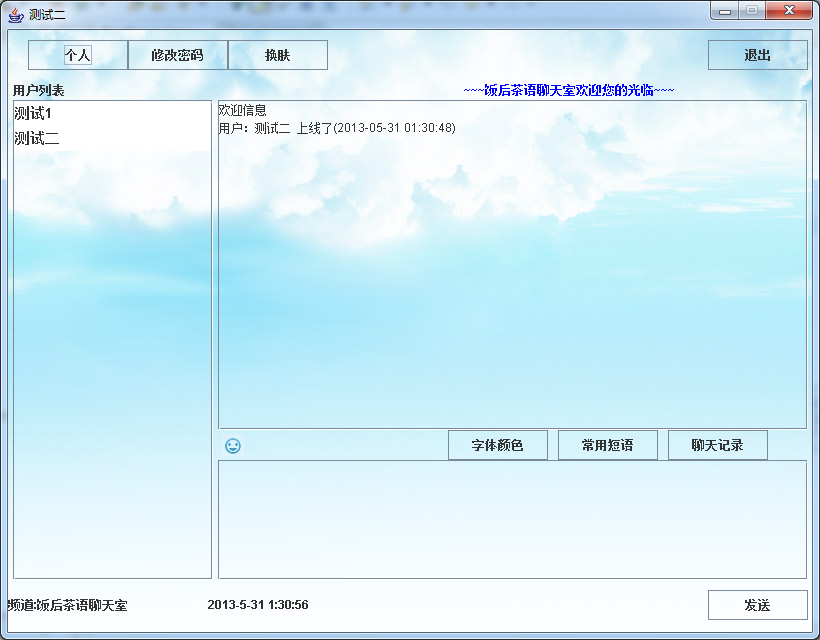
文件传输与聊天系统设计
技术:Java等摘要:本文介绍了一种基于TCP/IP协议使用Socket技术实现的聊天室系统,包括私聊功能和文件传输功能,对系统的主要模块进行了分析,并对系统实现过程中遇到的关键性技术进行了阐述,最后对系统进行了…...
蓝桥杯第十四届校内赛(第三期) C/C++ B组
一、填空题 (一)最小的十六进制 问题描述 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作…...

有关平方或高次方的公式整理一元高次方程的求解
Part.I Introduction 这篇博文记录一下数学中常用的有关平方或高次方的一些公式。 Chap.I 一些结论 下面一部分汇总了一些重要的结论 完全平方公式:(ab)2a22abb2(ab)^2a^22abb^2(ab)2a22abb2平方差公式:a2−b2(ab)(a−b)a^2-b^2(ab)(a-b)a2−b2(ab)(…...

Java笔记3
ArrayListArrayList<String> list new Arraylist<>();<>是泛型表示存放的数据类型,注意不能是基本数据类型;增删改查增:add 返回值为true删:remove 1.直接删元素2.根据索引删元素改:set(…...

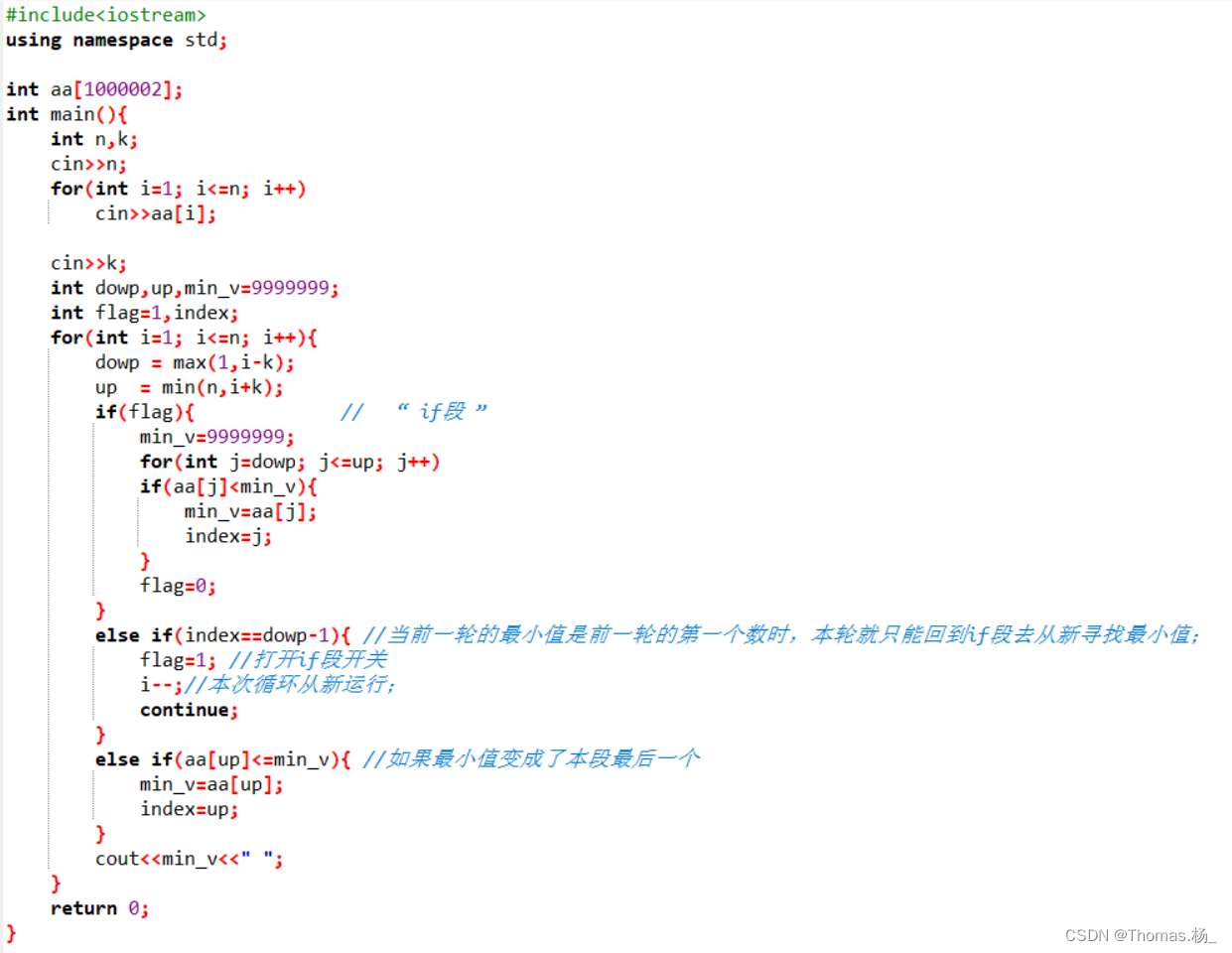
Leetcode.2202 K 次操作后最大化顶端元素
题目链接 Leetcode.2202 K 次操作后最大化顶端元素 Rating : 1717 题目描述 给你一个下标从 0开始的整数数组 nums,它表示一个 栈 ,其中 nums[0]是栈顶的元素。 每一次操作中,你可以执行以下操作 之一 : 如果栈非空…...

JAVA知识点全面总结3:String类的学习
三.String类学习 1.String,StringBuffer,StringBuilder的区别? 2.字符串拼接用加号的原理 ? 3.字符串常量池如何理解? 4.String的intern方法理解? 5.String的equals方法和compareTo方法的使用…...
Eureka注册中心和Nacos注册中心详解以及Nacos与Eureka有什么区别?
目录:前言Eureka注册中心Nacos注册中心Nacos与Eureka有什么区别?前言提供接口给其它微服务调用的微服务叫做服务提供者,而调用其它微服务提供的接口的微服务则是服务消费者。如果服务A调用了服务B,而服务B又调用了服务C࿰…...

Web3D发展趋势以及Web3D应用场景
1,Web3D发展趋势随着互联网的快速发展,Web3D技术也日渐成熟,未来发展趋势也值得关注。以下是Web3D未来发展趋势的七个方面:可视化和可交互性的增强:Web3D可以为三维数据提供可视化和可交互性的增强,将极大地…...

2023-3-4 刷题情况
按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length 0 < j < nums.length 0 < k < nums.l…...
前端面试总结
1.引言 最近参加了大量的招聘会,投递了大量的简历,整整体会了从“随便找个厂上一下”——“还是的找个大厂”——“没人要”——“急了急了,海投一波”——“工资有点尬”——“海投中…”。简单说一下自己的一些感受吧,现在的前端属实有点尴…...
: Spatial clustering)
Geospatial Data Science (6): Spatial clustering
Geospatial Data Science (6): Spatial clustering 1.Clustering, spatial clustering, and geodemographics 本节涉及空间观测的统计聚类。许多问题和主题都是复杂的现象,涉及多个维度,难以归纳为一个单一的变量。在统计学术语中,我们把这一类问题称为多变量,而不是在…...

蚁群算法优化问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 50; %蚂蚁个数 Alpha 1; %信息素重要程度参数 Beta 5; %启发式因子重要程度参数 Rho 0.1; %信息素蒸发系数 G 20…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
