光速c数列的猜想:光猜
光速c数列的猜想:光猜
2023-03-05 10:26:30
猜测:不同的宇宙光速c并不同
分成等级数列c0,c1,c2,...cn...
地球所处宇宙的真空光速c为c1,其中c0或许假设为光在纯水中速度乎
亦有可能仅有六级对应六道。
宇宙外,容器外也,超过光速c1,为光速c2,可看到容器内c1的景象?
象人类看到动物乎?
什么事在c2内可逆反c1?什么事仍然不可,要在c3中才可?全部猜叉
猜测:不同的宇宙光速c并不同(续):光猜(续)
当年麦哲伦环绕地球一圈,也是偶然才发现地球是圆的。
同理,如果有人类宇宙飞船以光速向着北极星方向飞去,估计可能会历史重演,或许会发现,不停的光速飞行,居然绕了宇宙一圈,但是,并没有到达北极星,这是怎么回事呢。估计,这个北极星,有可能就类似地球与月亮太阳的航海定位方向的作用,原来,以光速飞行时,地球所在的宇宙居然可能是一个类似地球的无形的四维时空球体,但是地球人是看不见摸不着的,如同人在地球上不知地球是圆的一样。
而在北极星所处宇宙的生命,看地球的宇宙,如同地球人看水中鱼一样。
设想北极星所处的中层宇宙的光速是c2,它的光以光速c2到达地球所在的宇宙容器不是以地球光速c1来到过的,而是以快得多的c2来到达地球的宇宙边界的,然后进入到达地球时才是c1的,如同光进入地球水中时一样,而且不知会不会折射象水中折射一样。而相对论认为是光到达大质量天体时(如太阳是绝对圆的假设等等)会时空弯曲来解释一样。
而北极星所处宇宙的生命估计比地球人长得多,象地球人比水中鱼的寿命和智慧和生活质量一样高长得多一样。
以上是估计猜测而来的,一切靠估的,不是真的,当作看小说罢,科幻小说看得多了,这样的估计猜测不足为奇。
论精神的物质投影猜想(论物体的电动力学)论无穷大与无穷小的对应映射
鱼在水中,不知环境水为何物,只是凭感觉知道感觉有物。人在陆地,知道水与空气不同样。古人在陆地,知道和风拂面感觉不同,不知风为空气物质。
推理,空气没有后,真空与空气不同样。真空空间也是层次的,不是同一个真空的。
不同层次的真空,光速C不同样,形成光速数列Ci。光速数列Ci可能与大环境中的重力场有关,一层层剥洋葱皮一样的剥去,真空就一层层光速不同样乎。
同理,假设猜想精神为物,精神常驻体内,犹如鱼在水中,又如人在空气中乎。
同理,精神本身也是分成一层层,象光速C一样形成数列Ji乎,jing为精的拼音,i为下标乎。
最原始的精神,象量子一样最小微粒,人人一样平等乎。
因为一层层,层者象尘,六层泥尘所覆盖,所以,象衣服一样,人就表现出各向异性?实现上最小微粒,人皆各向同性?
==以上仅是猜测,当作笑谈,不可当真也。
论无穷大与无穷小的对应映射
假设小数分为a.b,无限不循环小数形成无理数.b,假设,数轴上的方向相反,a.b变成b.a,那么无穷大的b部分发散,其实映射着小数.b是收敛的,阴阳互换,任一个无限大a,必有一个无限小的无理数或有理数(有理数循环小数)与之对应,此即有阴必有阳。
所以,任一个无穷大数,必定对应映射一个无穷小数,反之一样,不存在一个单一的孤阴寡阳存在。
所以,同样是自然数的无穷大数字,总有一个无穷小数或无理数与之对应着。
无穷大于是可以用其对应的无穷小数的反射数来表示乎。
所以,鱼在水中,人在空气中,可以向无穷大推出真空的层层分级,又可以向无穷小推出精神的层层细分量子最小微粒乎。
所以,中观为已知下,向宏观层层叠代,又向微观层层映射乎
以上皆为猜测,不能作为任何决策的依据,否则后果自负,与本人的猜测无关,事先免责声明。
相关文章:

光速c数列的猜想:光猜
光速c数列的猜想:光猜 2023-03-05 10:26:30 猜测:不同的宇宙光速c并不同 分成等级数列c0,c1,c2,...cn... 地球所处宇宙的真空光速c为c1,其中c0或许假设为光在纯水中速度乎 亦有可能仅有六级对应六道。 宇宙外,容器外也,超过光速c1,为光速c2,可看到容器…...

2023年全国最新交安安全员精选真题及答案12
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 21.作业场所监督检查是安全生产监督管理的一种重要形式,作业场所监督…...

2023年全国最新安全员精选真题及答案14
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 81.(单选题)正常工作状态下,高处作业吊篮悬挂机构抗…...

让Vue响应Map或Set的变化操作,在vue中响应map和set数据结构,计算属性的用法,计算属性特点
明确一点 vue的响应式系统不支持Map和Set,也就是说,当Map与Set里面的元素变化时Vue追踪不到这些变化,因此无法做出响应。 如下demo其实是不会进行数据相应的 <h1 v-for"(item,index) in mySetAsList" :key"index"&…...
Unable to find a valid cuDNN algorithm to run convolution
Unable to find a valid cuDNN algorithm to run convolution 今天在复习HumanNerf的时候发现了这个报错, import torch print(torch.cuda.is_available()) 使用上面的代码发现GPU是可以用的,可自己的torch版本对应。 后面继续看帖子,总结有…...

Linux 进程:进程退出返回值的获取
目录一、对输出参数status的理解二、获取进程退出返回值1.位运算(1)异常退出码(2)进程返回值2.宏函数我们常使用函数 wait 和 waitpid 来执行进程等待的功能:处理退出的子进程并释放资源,防止子进程变成僵尸进程。而这两个函数都有一个输出参数status&am…...

JavaScript核心高级内容复习1
本节概述 数据类型的分类和判断 基本(值)类型 Number ----- 任意数值 -------- typeofString ----- 任意字符串 ------ typeofBoolean ---- true/false ----- typeofundefined — undefined ----- typeof/null -------- null ---------- 对象(引用)类型 Object ----- typeof…...

2D图像处理:Qt + Opencv使用光度立体法检测Halcon中提供的缺陷图像
文章目录 不需知道光源方向一、光度立体法(后续有时间在查资料研究)1.1 问题1:Slants和Tilts的理解(暂时是理解的)1.2 问题1:Gradient通道数为1,为何像素点对应的值会有两个?1.3 问题2:F(r,c)=(u(r,c),v(r,c)) 关于高斯曲率和平均曲率如何计算的?二、非标定光源实现光…...

怎样用sql去查一个订单表中一个店铺一段时间的营业收入的环比
一:思路 要查询一个订单表中一个店铺一段时间的营业收入的环比,可以按照以下步骤进行操作: 使用SELECT语句选择需要的数据列,如订单日期和订单金额,以及店铺名称列。 使用WHERE语句过滤出指定店铺和时间段的订单数据…...
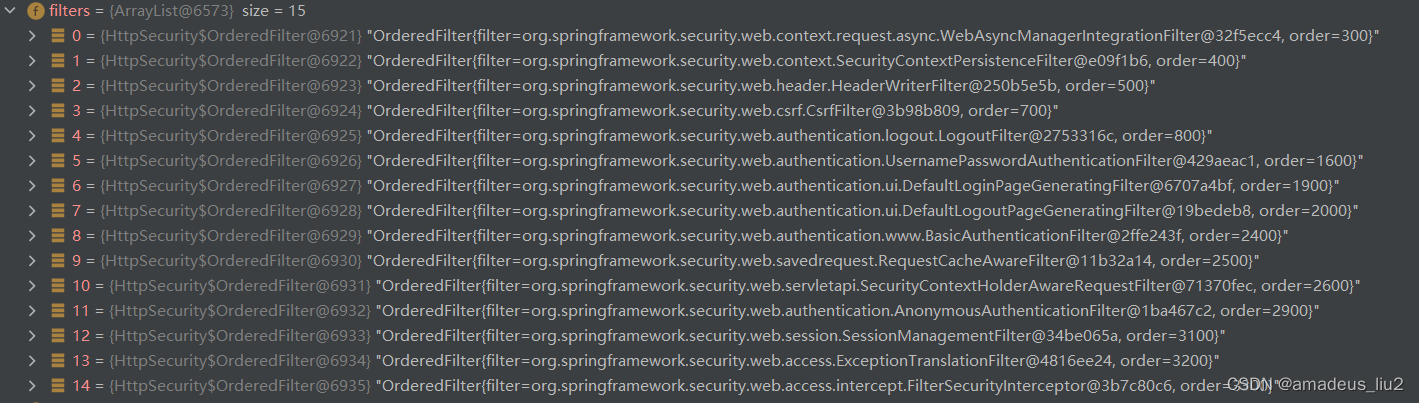
SpringSecurity: 默认添加的15个Filter是怎么添加进去的?
总的流程分为两部分,一是先用Map把configurer收集起来,然后再把maper中所有的configurer应用到HttpSecurity对象。 其中的map位于AbstractConfiguredSecurityBuilder这个类。 private final LinkedHashMap<Class<? extends SecurityConfigurer&l…...

学习记录---latent code 潜在编码
文章目录参考文献1. 什么是潜在编码?2.什么是潜在空间?3.同类潜在编码的相似性4.潜在编码的应用4.1 Antoencoders4.2 Generative models5.结论个人学习总结,持续更新中……参考文献 [1] 快速理解深度学习中的latent code潜在编码 1. 什么是…...
Cesium三维数据格式以及生产流程详解(glb,osgb,obj,bim,ifc)等
最近收到私信问我在cesium上展示的一些三维数据是如何生产和处理的,这篇文章就给大家一次性讲个透彻。 首先我们来做做分类。市面上能接触到的,常见的,cesium上支持展示的三维数据大致分为以下几种: 1.倾斜摄影(osgb,obj) 2.点云数据(las,pts) 3.手工模型(gltf,…...
)
2023年备考信息安全工程师每日知识点(1)
信息安全工程师在软考中属于中级认证,难度尚可,如果从今天开始学的话,肯定来得及 作者简介: 吉林师范大学网络空间安全的一名普通的大一学生已于2022年拿到华为阿里腾讯三家认证吉师信网中心的一名可怜打工人华为MindSpore截至目…...

Unity记录3.1-地图-TileMap简单使用、鼠标拖动放置Tile
文章首发及后续更新:https://mwhls.top/4456.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 汇总:Unity 记录 上章的课程接下来是巡逻的敌人…...
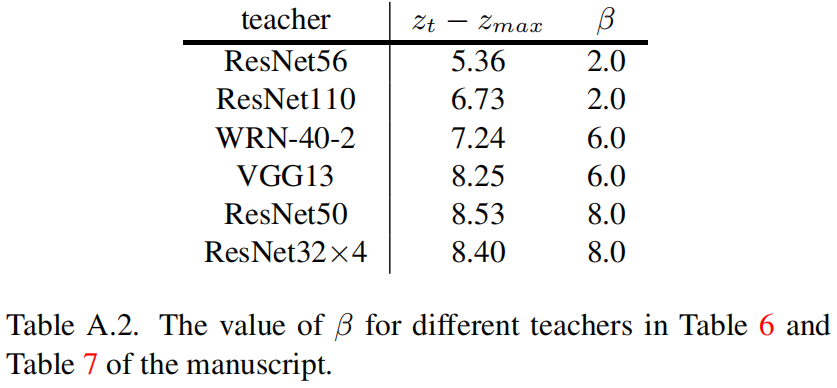
Decoupled Knowledge Distillation(CVPR 2022)原理与代码解析
paper:Decoupled Knowledge Distillationcode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/DKD.py背景与基于响应logits-based的蒸馏方法相比,基于特征feature-based的蒸馏方法在各种任务上的表现更好…...

IronWebScraper 2023.2.2 Crack
关于 .NET 的 IronWebScraper 用于从 HTML Web 应用程序中提取干净的结构化数据的 C# 框架。 IronWebScraper for .NET 是一个 C# 网络抓取库,它允许开发人员模拟和自动化人类浏览行为,以从 Web 应用程序中提取内容、文件和图像作为本机 .NET 对象。Iron…...

【2.1 golong中条件语句if】
1. 条件语句if 1.1.1. Go 语言条件语句: 条件语句需要开发者通过指定一个或多个条件,并通过测试条件是否为 true 来决定是否执行指定语句,并在条件为 false 的情况在执行另外的语句。 Go 语言提供了以下几种条件判断语句: 1.1…...
)
Scala编程(第四版)
Scala编程可伸缩的语言面向对象与函数式编程Scala优势Scala是兼容的可伸缩的语言 1、适合构建将java组件组装在一起的脚本 2、用于编写可复用组件,并讲这些组件构建成大型框架 Scala是一门综合面向对象和函数式编程概念的静态类型编程语言 面向对象与函数式编程 面…...
aws apigateway 基础概念和入门示例
参考资料 https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started.html apigateway基础理解 apigateway的核心概念 apigateway,基础服务用来管理接口的创建,部署和管理restapi,http资源和方法的集合&#…...
2023年“中银杯”安徽省职业院校技能大赛网络安全A模块全过程解析
A模块基础设施设置/安全加固(200分) 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用登录和密码策略、流量完整性保护策略、事件监控策略、防火墙策略等多种安全策略来提升服务器系统的网络安全…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
