P1228 地毯填补问题(葬送的芙蓉王【bushi】)
地毯填补问题
题目描述
相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地方盖上,美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住,毯子的形状有所规定,只能有四种选择(如图):

并且每一方格只能用一层地毯,迷宫的大小为 2 k × 2 k 2^k\times 2^k 2k×2k 的方形。当然,也不能让公主无限制的在那儿等,对吧?由于你使用的是计算机,所以实现时间为 1 1 1 秒。
输入格式
输入文件共 2 2 2 行。
第一行一个整数 k k k,即给定被填补迷宫的大小为 2 k × 2 k 2^k\times 2^k 2k×2k( 0 < k ≤ 10 0\lt k\leq 10 0<k≤10);
第二行两个整数 x , y x,y x,y,即给出公主所在方格的坐标( x x x 为行坐标, y y y 为列坐标), x x x 和 y y y 之间有一个空格隔开。
输出格式
将迷宫填补完整的方案:每一补(行)为 x y c x\ y\ c x y c( x , y x,y x,y 为毯子拐角的行坐标和列坐标, c c c 为使用毯子的形状,具体见上面的图 1 1 1,毯子形状分别用 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4 表示, x , y , c x,y,c x,y,c 之间用一个空格隔开)。
样例 #1
样例输入 #1
3
3 3
样例输出 #1
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
提示
spj 报错代码解释:
- c c c 越界;
- x , y x,y x,y 越界;
- ( x , y ) (x,y) (x,y) 位置已被覆盖;
- ( x , y ) (x,y) (x,y) 位置从未被覆盖。
upd 2023.8.19 \text{upd 2023.8.19} upd 2023.8.19:增加样例解释。
样例解释
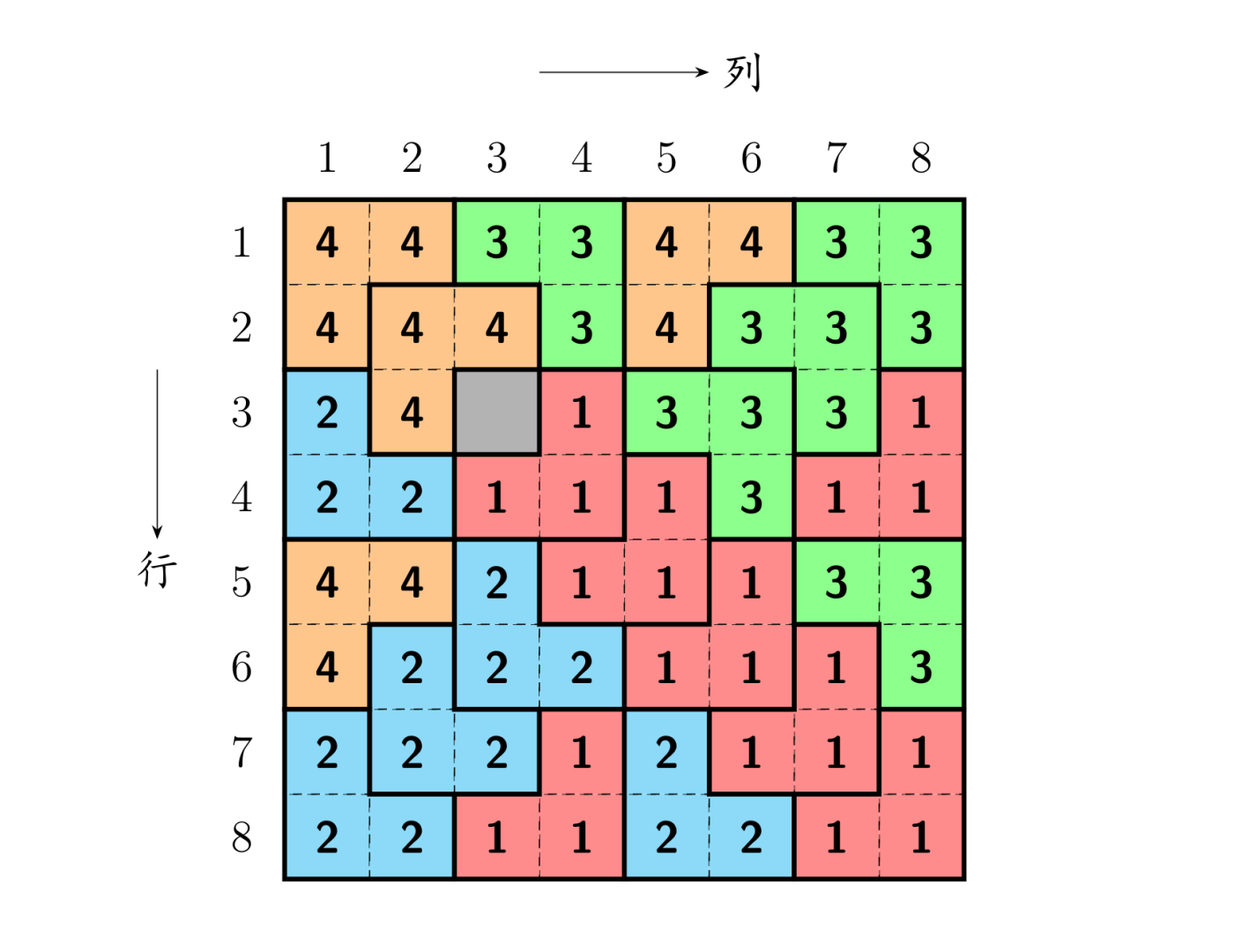
大致思路
当k=1时,我们可以非常容易得到毯子填补的方案。当k=2甚至更大时,我们可以将其划分为四大块,但是公主位只有一个,而对于其他没有公主位的四方格,似乎和原问题形式不一样。但是我们可以对其加以处理,使其四个子问题都具有相同形式——即,我们可以手动为其他三个没有公主位的四方格增加新的“公主位”。例如,当公主位在左上角时,我们可以将剩余三个四方格的交界处用毯子1来补上,这样每个四方格都会被分配到一个公主位,称为特殊的方阵,问题便迎刃而解(如图所示)。因此我们就可以采用分治的方法去不断将正方形划分为4个子正方形,再分别填充,直到小正方形边长为1时,就是公主位了,不用做任何处理。
8x8的方格里,公主在右上角的格子里,然后在左上角的4x4方格中,选右下角,在左下角的方格中,选右上角,在右下角的方格中,选左上角,组成一个L,现在一个8x8的方格被分为四个4x4的方格,每个4x4的方格中,都有一块被挖掉的部分,左上角的4*4方格中被挖掉的部分是它右下角组成L的那一块,右上角的4x4方格中,挖去的是公主的位置,左下角和右下角的方格,挖去的都是L那部分
然后对每个4x4方格,重复以上操作,直到方格划分为2*2的,四个格子中有一个被挖去,另外三个自然组成一个L
AC CODE
#include<bits/stdc++.h>
using namespace std;// 正方形左上角坐标xx和yy,公主坐标x和y,正方形边长k
void work(int xx,int yy,int x,int y,int k){if(k == 1) return;k/=2;// 左上角if(x < xx+k && y < yy+k){printf("%d %d %d\n",xx+k,yy+k,1);// 递归覆盖左上角work(xx,yy,x,y,k);// 覆盖右下角work(xx+k,yy+k,xx+k,yy+k,k);// 覆盖左下角work(xx+k,yy,xx+k,yy+k-1,k);// 覆盖右上角work(xx,yy+k,xx+k-1,yy+k,k);}// 右上角else if(x < xx+k && y >= yy+k){printf("%d %d %d\n",xx+k,yy+k-1,2);// 递归覆盖左上角work(xx,yy,xx+k-1,yy+k-1,k);// 覆盖右下角work(xx+k,yy+k,xx+k,yy+k,k);// 覆盖左下角work(xx+k,yy,xx+k,yy+k-1,k);// 覆盖右上角work(xx,yy+k,x,y,k);}// 左下角else if(x >= xx+k && y < yy+k){printf("%d %d %d\n",xx+k-1,yy+k,3);// 递归覆盖左上角work(xx,yy,xx+k-1,yy+k-1,k);// 覆盖右下角work(xx+k,yy+k,xx+k,yy+k,k);// 覆盖左下角work(xx+k,yy,x,y,k);// 覆盖右上角work(xx,yy+k,xx+k-1,yy+k,k);}// 右下角else{printf("%d %d %d\n",xx+k-1,yy+k-1,4);// 递归覆盖左上角work(xx,yy,xx+k-1,yy+k-1,k);// 覆盖右下角work(xx+k,yy+k,x,y,k);// 覆盖左下角work(xx+k,yy,xx+k,yy+k-1,k);// 覆盖右上角work(xx,yy+k,xx+k-1,yy+k,k);}
}int main()
{int x,y,k;cin >> k >> x >> y;work(1,1,x,y,(1 << k));return 0;
}相关文章:

P1228 地毯填补问题(葬送的芙蓉王【bushi】)
地毯填补问题 题目描述 相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地…...
)
352. 闇の連鎖(树上差分,LCA)
352. 闇の連鎖 - AcWing题库 传说中的暗之连锁被人们称为 Dark。 Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。 经过研究,你发现 Dark 呈现无向图的结构,图中有 N 个节点和两类边,一类边被称为主要边ÿ…...

dcat admin + dingo + nginx 开发前台
前言 Dcat Admin 是一个功能强大的后端框架,主要用于开发管理后台。然而,大多数网站不仅需要一个管理后台,还需要一个用户界面,即“前台”,以及它们自己的用户系统。 为了实现这一目标,我们需要对 Dcat A…...
安卓线性布局LinearLayout
<?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:tools"http://schemas.android.com/tools"android:layout_width"match_parent"android:…...
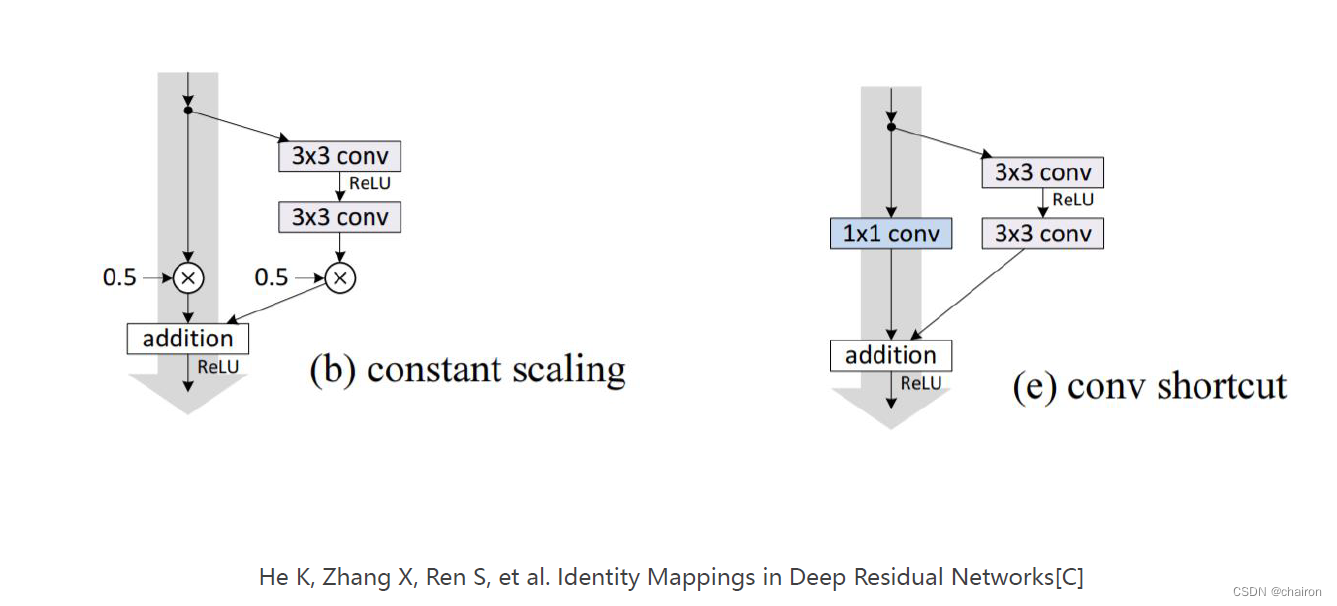
Advanced CNN
文章目录 回顾Google NetInception1*1卷积Inception模块的实现网络构建完整代码 ResNet残差模块 Resedual Block残差网络的简单应用残差实现的代码 练习 回顾 这是一个简单的线性的卷积神经网络 然而有很多更为复杂的卷积神经网络。 Google Net Google Net 也叫Inception V…...
判断当前设备是不是安卓或者IOS?
代码(重要点): 当前文件要是 xxx.js文件,就需要写好代码后调用才会执行: // 判断是不是安卓 const isAndroid () > {return /android/.test(navigator.userAgent.toLowerCase()); }// 判断是不是ios const isIOS () > {return /iphone|ipad|ipod/.test(navigator.use…...

使用C++操作Matlab中的mat文件
matlab提供读写MAT文件的头文件和库函数,下面列出这些文件的路径,其中matlabroot指matlab安装的路径,arch来识别平台架构 头文件在matlabroot\extern\include库函数在matlabroot\bin\win64例程在matlabroot\extern\examples\eng_mat头文件 …...

【OCPP】ocpp1.6协议第3.5章节:本地授权和离线行为-介绍及翻译
目录 3.5章节 概述 3.5 本地鉴权和离线行为-译文(Local Authorization & Offline Behavior) 3.5.1 鉴权缓存-译文(3.5.1. Authorization Cache) 3.5.2 本地鉴权列表-译文(Local Authorization List) 3.5.3 授权缓存和本地授权列表之间的关系-译文(Relation between A…...

OpenGL查询对象 Query Objects
查询对象和异步查询(Query Objects and Asynchronous Queries) Query Objects(查询对象)是OpenGL中的一种机制,用于获取有关一系列GL命令处理过程的信息。这些信息可以包括: 绘图命令处理的图元数量。写入变换反馈缓冲区的图元数…...

【数据分享】1929-2023年全球站点的逐日最高气温数据(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据! 之前我们分享过1929-2023年全球气象站…...
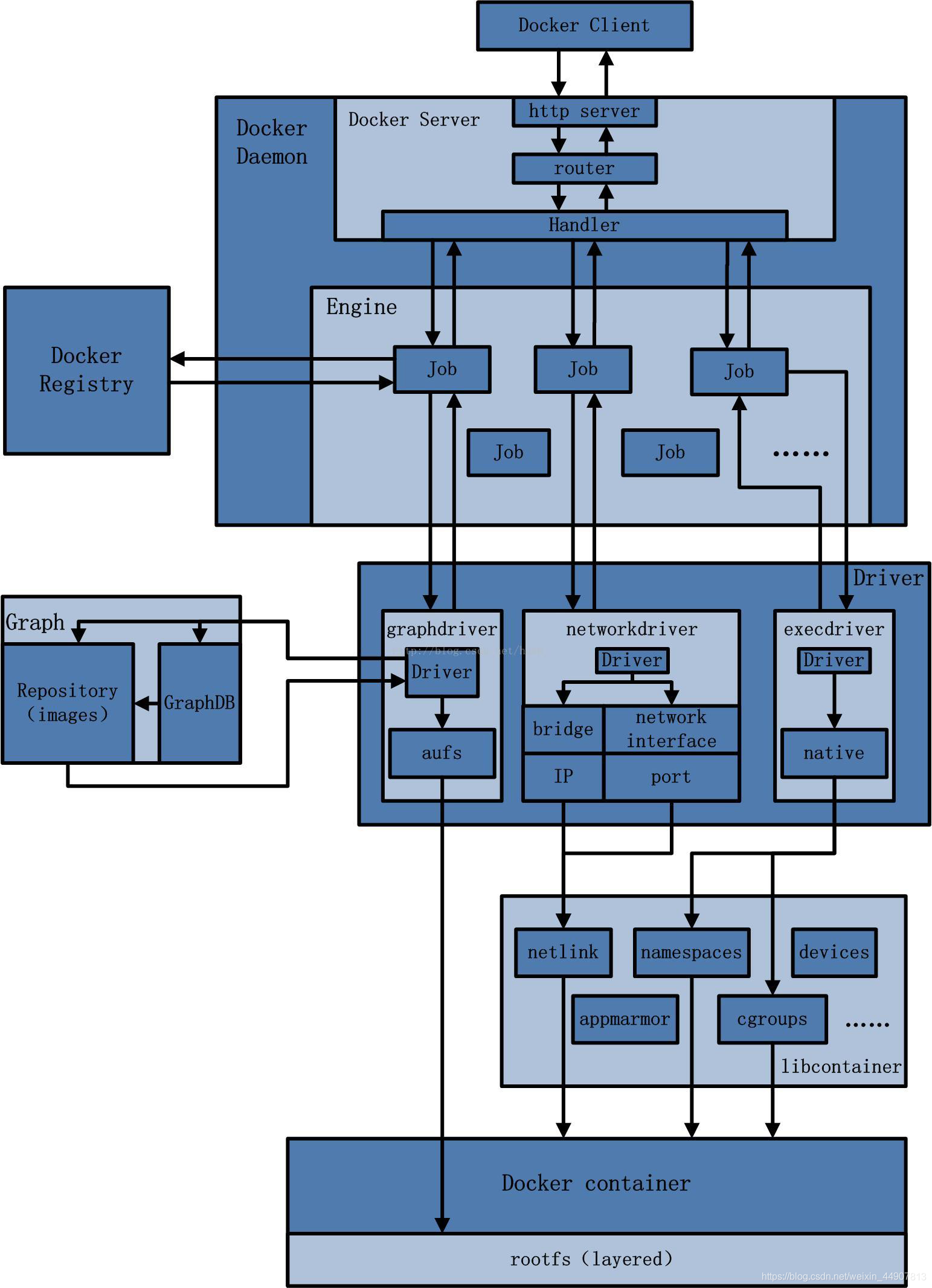
Docker深入解析:从基础到实践
Docker基础知识 Docker是什么:定义和核心概念解释 Docker是一个开源项目,它诞生于2013年,旨在自动化应用程序的部署过程, 让应用程序能够在轻量级的、可移植的、自给自足的容器中运行。这些容器可以在几乎任何机器上运行…...
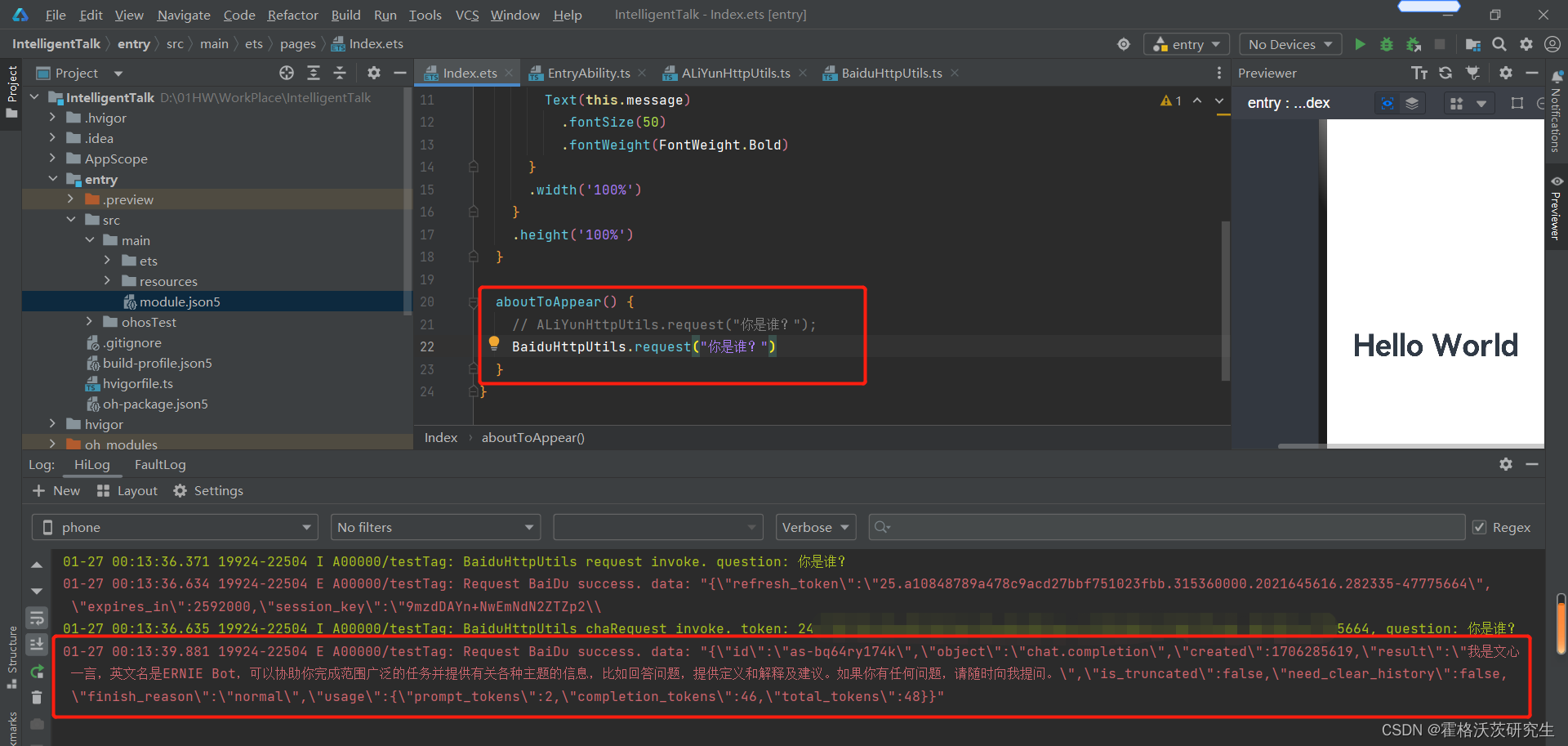
【鸿蒙】大模型对话应用(一):大模型接口对接与调试
Demo介绍 本demo对接阿里云和百度的大模型API,实现一个简单的对话应用。 DecEco Studio版本:DevEco Studio 3.1.1 Release HarmonyOS API版本:API9 关键点:ArkTS、ArkUI、UIAbility、网络http请求、列表布局 官方接口文档 此…...

SQL的函数类型
目录 一、聚合函数 二、数值型函数 三、字符串函数 四、日期函数 五、流程控制函数 一、聚合函数 定义:聚合函数是指对一组值进行运算,最终返回是单个值,也可以被称为组合函数。 COUNT() 统计目标行数量的函数 AVG() 求平均值 SU…...
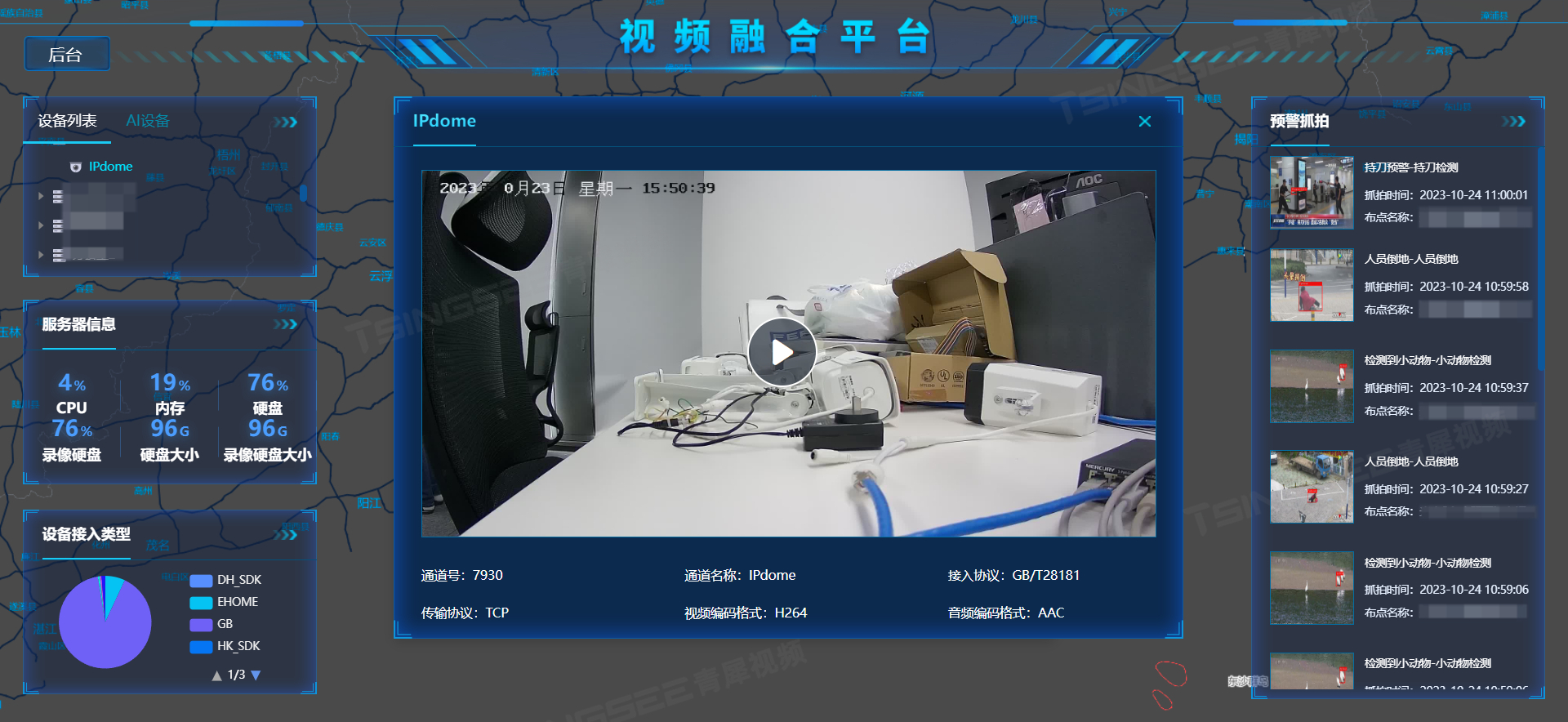
TSINGSEE青犀视频智慧电梯管理平台,执行精准管理、提升乘梯安全
一、方案背景 随着城市化进程的不断加快,我国已经成为全球最大的电梯生产和消费市场,电梯也成为人们日常生活中不可或缺的一部分。随着电梯数量的激增,电梯老龄化,维保数据不透明,物业管理成本高,政府监管…...

VMware:在部分链上无法执行所调用的函数,请打开父虚拟磁
VMware:在部分链上无法执行所调用的函数,请打开父虚拟磁 问题:VMware给虚拟机扩展硬盘容量,提示:在部分链上无法执行所调用的函数,请打开父虚拟磁。原因:是因为你的虚拟磁盘文件是分多个文件存储的…...
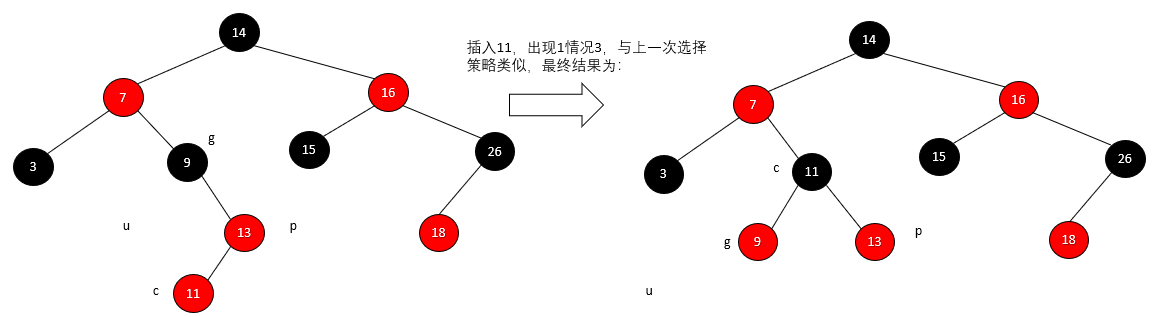
【数据结构 08】红黑树
一、概述 红黑树,是一种二叉搜索树,每一个节点上有一个存储位表示节点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长上两倍,因而是接进…...
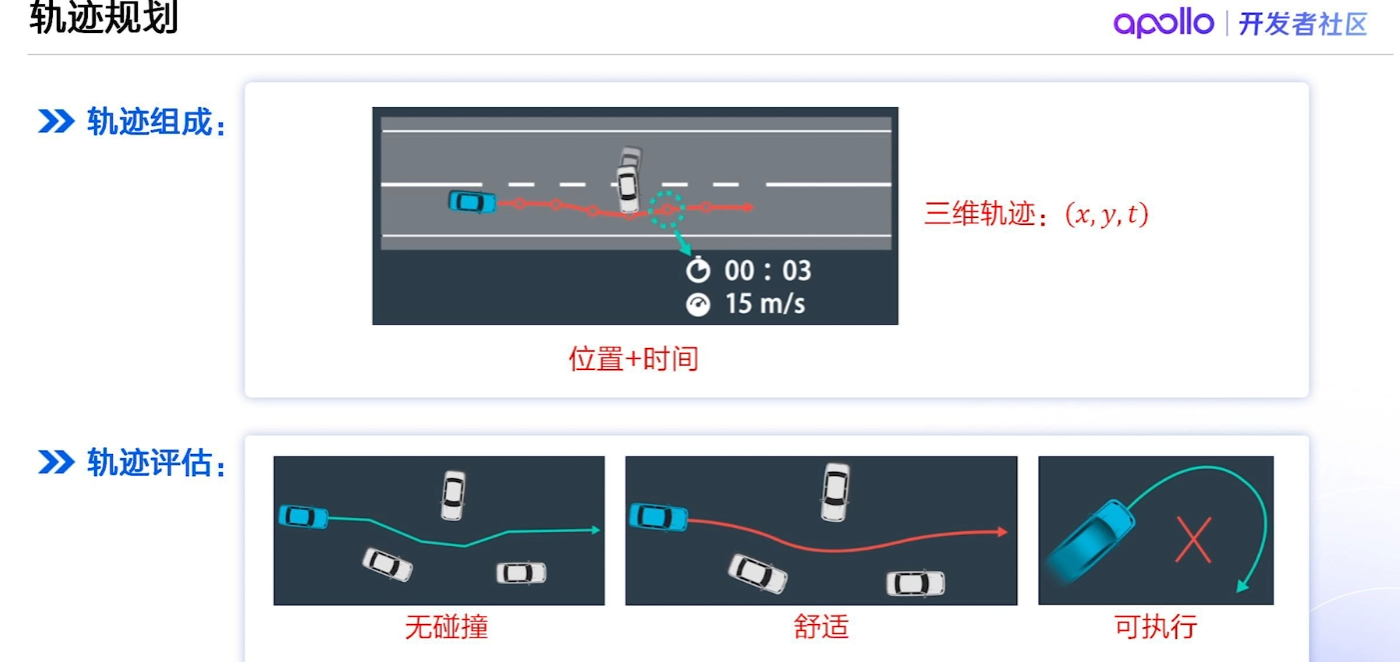
【百度Apollo】自动驾驶规划技术:实现安全高效的智能驾驶
🎬 鸽芷咕:个人主页 🔥 个人专栏:《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...

《C程序设计》上机实验报告(五)之一维数组二维数组与字符数组
实验内容: 1.运行程序 #include <stdio.h> void main( ) { int i,j,iRow0,iCol0,m; int x[3][4]{{1,11,22,33},{2,28,98,38},{3,85,20,89}}; mx[0][0]; for(i0;i<3;i) for(j0;j<4;j) if (x[i][j]>m) { mx[i][j]; iRowi…...

【BUG】联想Y7000电池电量为0且无法充电解决方案汇总
因为最近火灾很多,所以昨天夜晚睡觉的时候把插线板电源关掉了,电脑也关机了。 各位一定要注意用电安全,网上的那些事情看着真的很难受qvq。 第二天早上起床的时候一看发现电脑直接没电了,插上电源后也是显示 你一定要冲进去啊(ू˃…...

centos7常用命令之安装插件2
centos7安装插件1 7、kibana 【启动kibana,需要调整这个配置文件(/opt/kibana-6.3.0/config/kibana.yml)的一处ip地址,因为每次虚拟机的ip地址可能会有所不同, 同时访问页面地址的ip:5601时,ip地址也对应修改】 1.解压缩包 cd /opt/ tar -xvf kibana-6.3.0-linux-x…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
