LeetCode 热题 C++ 399. 除法求值 406. 根据身高重建队列
LeetCode 399
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]] 输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000] 解释: 条件:a / b = 2.0, b / c = 3.0 问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? 结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]] 输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]] 输出:[0.50000,2.00000,-1.00000,-1.00000]
提示:
1 <= equations.length <= 20equations[i].length == 21 <= Ai.length, Bi.length <= 5values.length == equations.length0.0 < values[i] <= 20.01 <= queries.length <= 20queries[i].length == 21 <= Cj.length, Dj.length <= 5Ai, Bi, Cj, Dj由小写英文字母与数字组成
思路:
Floyd.
可以把这个看成是一个图,求两点之间最短距离。
代码:
class Solution {
public:vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {vector<double> v;int n=0;unordered_map<string,int> m;for(int i=0;i<equations.size();i++){if(m.find(equations[i][0])==m.end())m[equations[i][0]]=n++;if(m.find(equations[i][1])==m.end())m[equations[i][1]]=n++;}vector<vector<double> >g(n, vector<double>(n, -1.0));for(int i=0;i<equations.size();i++){int a=m[equations[i][0]],b=m[equations[i][1]];g[a][b]=values[i];g[b][a]=1.0/values[i];}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if(g[i][k]>0&&g[k][j]>0)g[i][j]=g[i][k]*g[k][j];}}}for(int i=0;i<queries.size();i++){if(m.find(queries[i][0])==m.end()||m.find(queries[i][1])==m.end()){v.push_back(-1.0);continue;}int a=m[queries[i][0]],b=m[queries[i][1]];v.push_back(g[a][b]);}return v;}
};LeetCode406
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 解释: 编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。 编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。 编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。 编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。 编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]] 输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 20000 <= hi <= 1060 <= ki < people.length- 题目数据确保队列可以被重建
思路:
先排序,高个子排进去后,让个子矮的选位置。
代码:
class Solution {
public:vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {vector<vector<int>> v;sort(people.begin(),people.end(),[](const vector<int>& v1, const vector<int>& v2){return v1[0] > v2[0] || (v1[0]==v2[0]&&v1[1] < v2[1]);});for(int i=0;i<people.size();i++){v.insert(v.begin()+people[i][1],people[i]);}return v;}
};相关文章:

LeetCode 热题 C++ 399. 除法求值 406. 根据身高重建队列
LeetCode 399 给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。 另有一些以数组 queries 表示的问题,其…...
提升Mac使用性能的5大方法,CleanMyMacX 2023非常的好用哦~
近些年伴随着苹果生态的蓬勃发展,越来越多的用户开始尝试接触Mac电脑。然而很多人上手Mac后会发现,它的使用逻辑与Windows存在很多不同,而且随着使用时间的增加,一些奇奇怪怪的文件也会占据有限的磁盘空间,进而影响使用…...
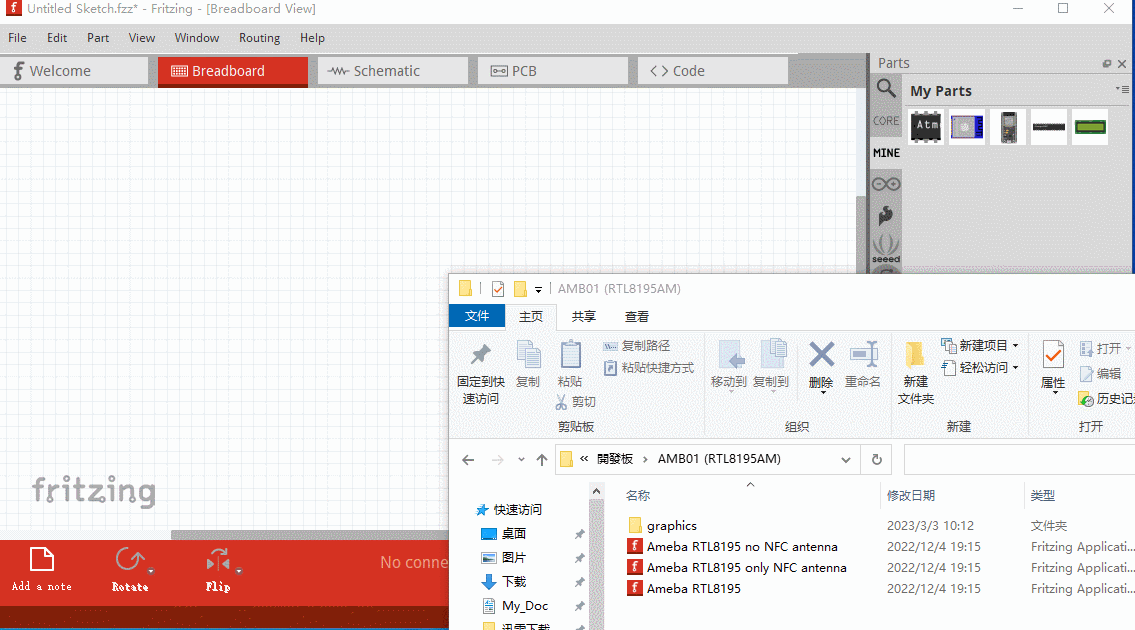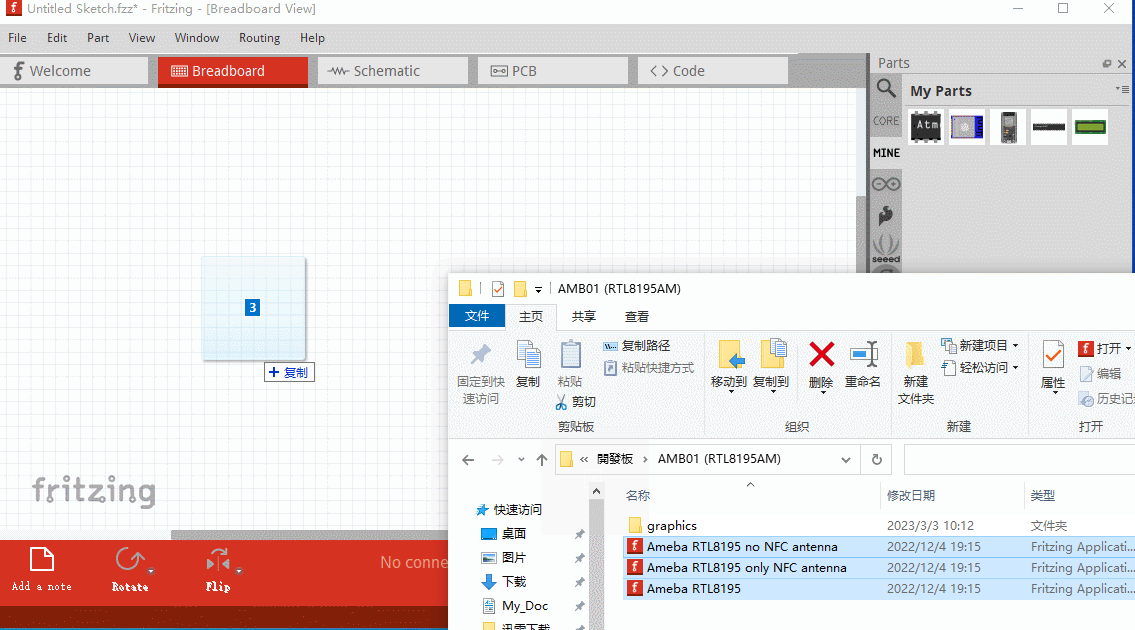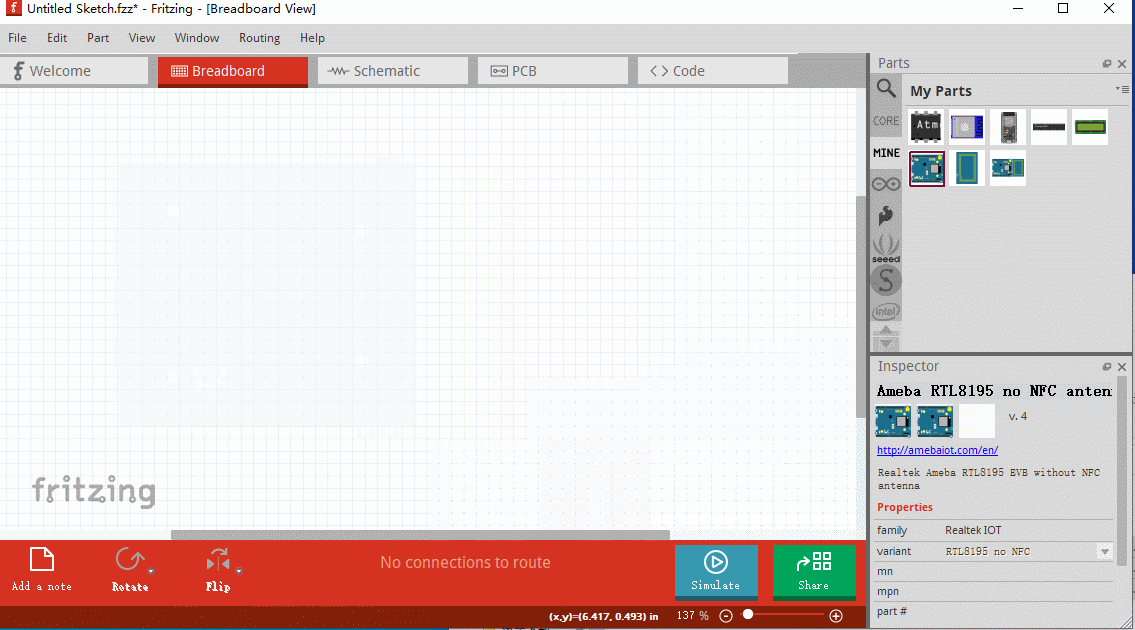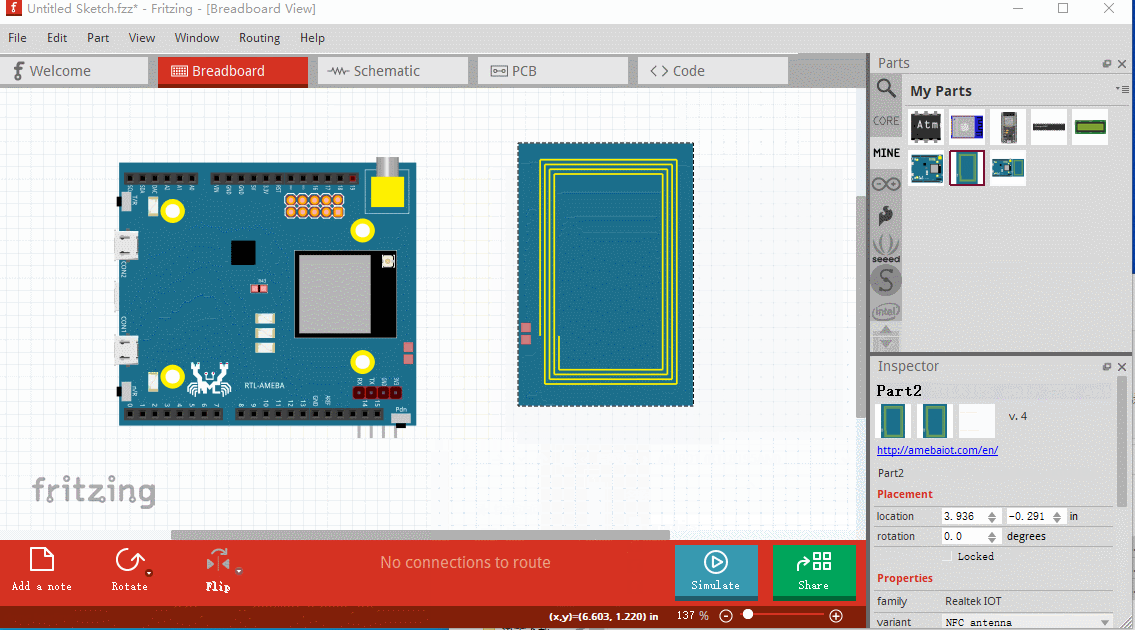
一步一步学会给Fritzing添加元器件-丰富你的器件库
文章目录1、获取元器件文件2、单个添加元器件3、批量加入(1)、通过别人发布的bin文件加载(2)、终极大招(拖)4、制作自己器件文章出处: https://blog.csdn.net/haigear/article/details/12931545…...

STM32 10个工程篇:1.IAP远程升级(一)
清晨一大早起来开始撰写STM32 10个例程篇的第一章即串口IAP远程升级,虽然网络上有很多免费和付费的STM32教程,但是仍然不断地说服自己沉住气、静下心写一份独一无二的,这份独一无二中也凝聚了一名MCU工程师5年间不断地项目迭代积累࿰…...

高通Android 13默认切换免提功能
1、测试部反馈 由于平板本身没有听筒功能 因此考虑工厂直接切换到免提功能 2、修改路径 frameworks/av/services/audiopolicy/enginedefault/src/Engine.cpp 3、编译源码ok 拨打紧急号码 可以正常切换到免提功能 其他mtk平台可能不一样 具体以项目实际为准 相关链接 构建…...
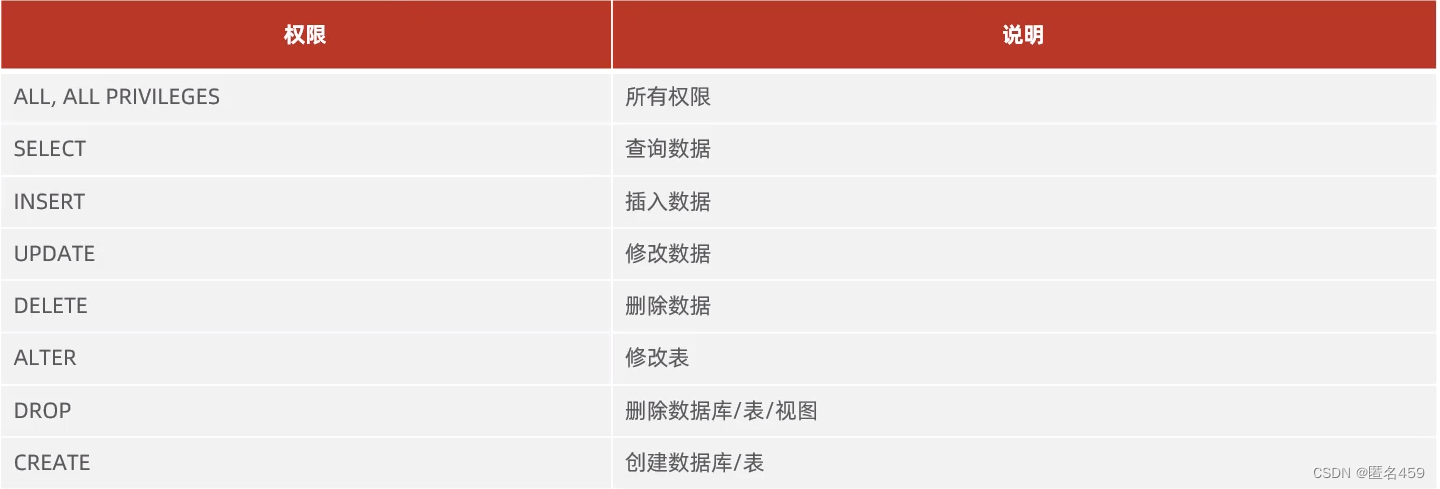
MySQL入门
Mysql入门SQL语句SQL通用语法SQL语句的分类DDL-数据库操作DDL-数据表操作DML-添加数据DML-修改、删除数据DQL-语法DQL-语句练习DCL-语法SQL语句 SQL通用语法 1、SQL语句可以单行或多行书写,以分号结尾。 2、SQL语句可以使用空格/缩进来增强语句的可读性。 3、MySQ…...

实验一 Python编程基础
目录 一、实验目标 二、实验内容 1.绘制如下图形 ,一个正方形,内有三个红点,中间红点在正方形中心。 2.使用turtle库绘制如下图形: 3.绘制奥运五环图 4.回文问题 5.身份证性别判别 6.数据压缩 7.验证哥德巴赫猜想 8.使…...
ThreadLocal介绍和理解)
java多线程(十五)ThreadLocal介绍和理解
一、对ThreadLocal的理解 ThreadLocal,很多地方叫做线程本地变量,也有些地方叫做线程本地存储,其实意思差不多。可能很多朋友都知道ThreadLocal为变量在每个线程中都创建了一个副本,那么每个线程可以访问自己内部的副本变量。这句…...
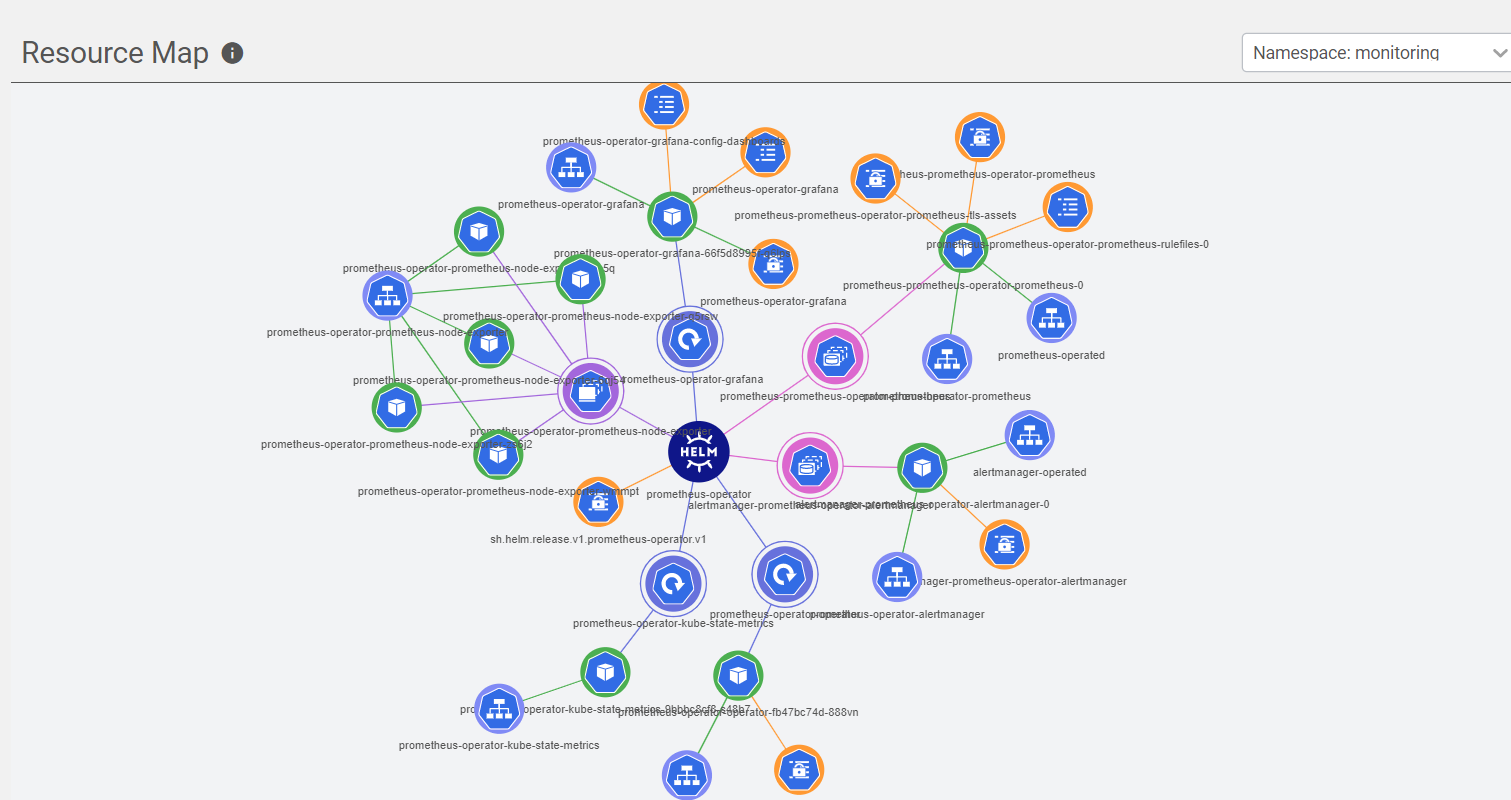
K8S 实用工具之三 - 图形化 UI Lens
开篇 📜 引言: 磨刀不误砍柴工工欲善其事必先利其器 第一篇:《K8S 实用工具之一 - 如何合并多个 kubeconfig?》第二篇:《K8S 实用工具之二 - 终端 UI K9S》 像我这种,kubectl 用的不是非常溜,经…...
HDMI协议介绍(六)--EDID
目录 什么是EDID EDID结构 1)Header Information 头信息(厂商信息、EDID 版本等) (2)Basic Display Parameters and Features 基本显示参数(数字/模拟接口、屏幕尺寸、格式支持等) (3)色度信息 (4)Established Timings(VESA 定义的电脑使用 Timings) (5)Standard Timing…...
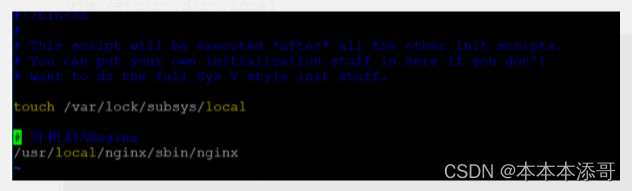
【项目实战】Linux下安装Nginx教程
一、环境准备 Linux版本:CentOS7 64位 二、具体步骤 2.1 步骤1:确认系统中安装以下基础依赖 确认系统中安装了gcc、pcre-devel、zlib-devel、openssl-devel。 在安装Nginx前首先要确认系统中安装了gcc、pcre-devel、zlib-devel、openssl-devel。 yu…...

【数据结构】链式二叉树
前言 在前面我们学习了一些二叉树的基本知识,了解了它的结构以及一些性质,我们还用数组来模拟二叉树建立了堆,并学习了堆排序,可是数组结构的二叉树有很大的局限性,平常我们用的最多树结构的还是链式二叉树,…...
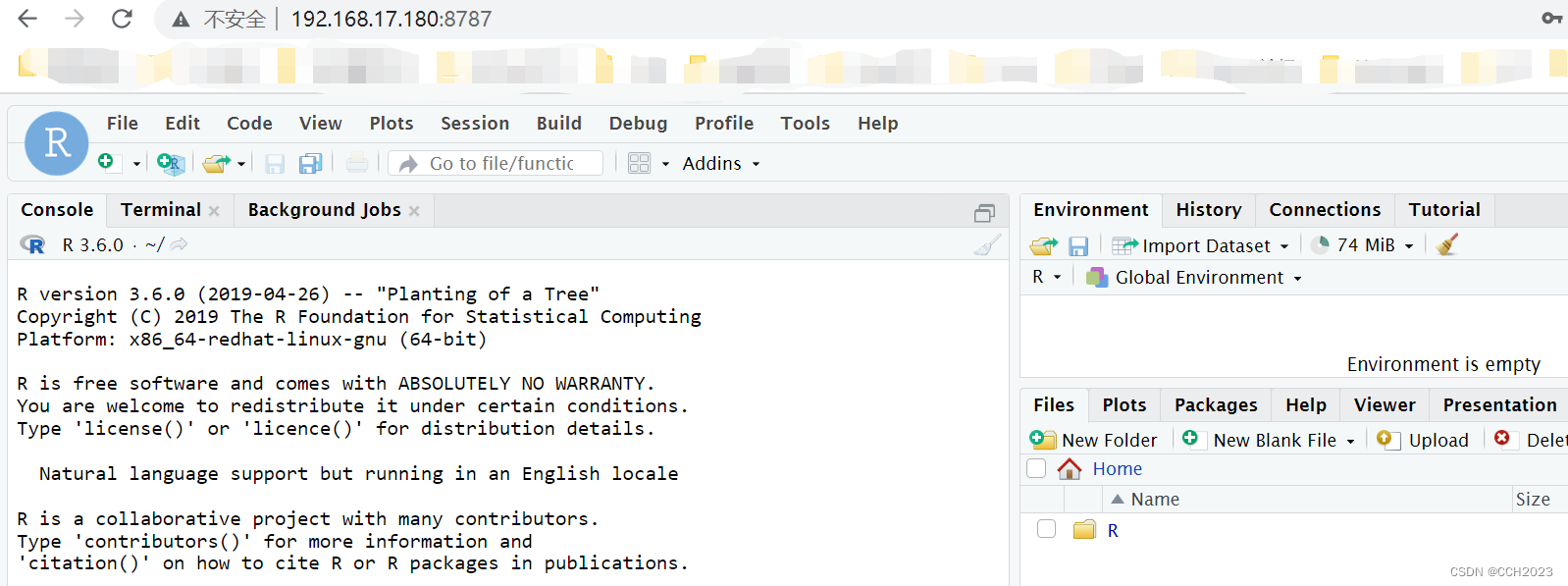
CentOS安装RStudio-Server的方法
R语言是生信分析、数据挖掘最常用最好用的软件之一,得到了广大生信工程师、数据分析师的厚爱。Rstudio 是 R 的集成开发环境,使得R语言的用户体验更强。一般个人电脑(PC, Personal Computer)使用单机版的 Rstudio 即可,…...

从交通信号灯看流控和拥塞控制
局部的效率和全局的公平一直都是矛盾的双方。对一个统计复用系统,局部效率由流控决定,而全局公平由拥塞控制决定。 交通信号灯是个典型的分时复用流控的实例,但我经常看到绿灯方向没有任何车辆通过,红灯方向却排成了长龙…...
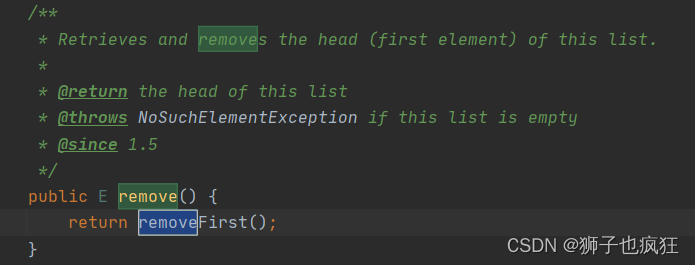
【LinkedList】| 深度剥析Java SE 源码合集Ⅰ
目录一. 🦁 LinkedList介绍二. 🦁 结构以及对应方法分析2.1 结构组成2.1.1 节点类2.1.2 成员变量2.2 方法实现2.2.1 添加add(E e)方法2.2.2 头尾添加元素Ⅰ addFirst(E e)Ⅱ addLast(E e)2.2.3 查找get(int index)方法2.2.4 删除remove()方法三. &#x…...
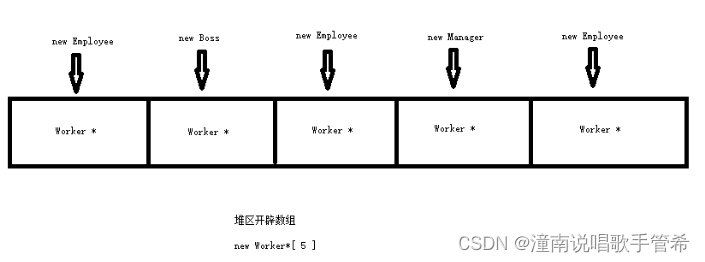
黑马程序员7
算数运算符重载 运算符重载概念:对已有的运算符重新进行定义,赋予其另一种功能,以适应不同的数据类型 加号运算符 通过自己写函数,实现两个对象相加属性后返回新的对象 两种方式重载 成员函数方式重载 全局函数重载 上来 perso…...
Qt安装与使用经验分享;无.pro文件;无QTextCodec file;Qt小试;界面居中;无缝;更换Qt图标;更换Qt标题。
1、切换安装下载源 《Qt安装教程》先推荐一篇安装文章:《Qt安装教程》 Qt 5.15 之后已经不提供离线安装包了,就是那个 3.7G 的 exe 安装包。请看官方说明,所以只能用在线安装包。 1,下载在线安装包 QT 在线安装包链接ÿ…...
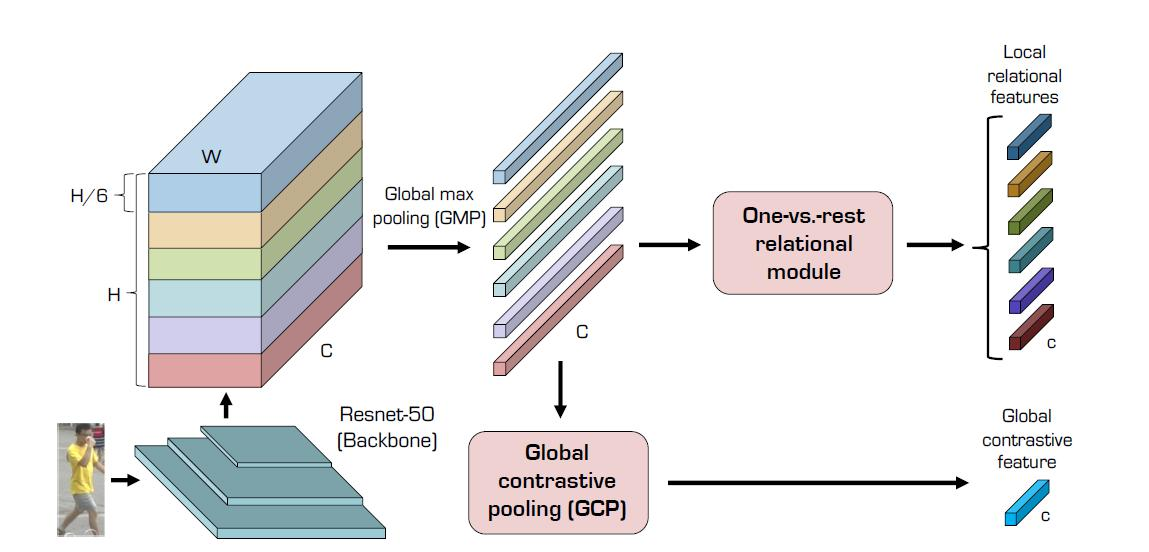
AAAI顶会行人重识别算法详解——Relation Network for Person Re-identification
1.论文整体框架概述 在行人重识别任务中,通常都是对整个输入数据进行特征提取,但是缺少了局部信息。能不能既考虑局部与整体信息,也同时加入他们的联系呢?这篇论文主要的思想就是局部信息和全局信息的融合。 整体流程如上图所示, 首先对整体进行特征提取, 通常采用…...
)
hadoop调优(二)
hadoop调优(二) 1 HDFS故障排除 1.1 NameNode故障处理 NameNode进程挂了并且存储数据丢失了,如何恢复NameNode? 如果NameNode进程挂掉并且数据丢失了,可以利用Secondary NameNode来恢复NameNode。Secondary NameNode主要用于备份NameNode…...

【基础算法】双指针---数组元素的目标和
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
