【动态规划】【数学】1388. 3n 块披萨
作者推荐
【动态规划】【字符串】【表达式】2019. 解出数学表达式的学生分数
本文涉及知识点
动态规划汇总
LeetCode1388 3n 块披萨
给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨:
你挑选 任意 一块披萨。
Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
示例 1:
输入:slices = [1,2,3,4,5,6]
输出:10
解释:选择大小为 4 的披萨,Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨,Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。
示例 2:
输入:slices = [8,9,8,6,1,1]
输出:16
解释:两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨,你的朋友们就会选择大小为 8 的披萨,这种情况下你的总和不是最大的。
提示:
1 <= slices.length <= 500
slices.length % 3 == 0
1 <= slices[i] <= 1000
动态规划
原理
题目等效于以下描述:
从[0,3n)中选择n个不相邻的数据,注意:0和3n-1是相邻。
题目一定符合描述: 因为相邻的数被Alice Bob 取走了。
描述一定符合题意,证明如下:
a,n=1,只有一个数必定不相邻。
b,n >1 。必定有两个选取的数之间有两个或以上的数。反证法:如果任何两个选取的数之间都只有一个数,那数的总数量是2n,和3n矛盾。对勾表示选取,X表示没选取。 ⋯ X ✓ X ‾ X ✓ X ⋯ \cdots \underline{ X \checkmark X} X \checkmark X \cdots ⋯X✓XX✓X⋯
我们将下划线部分删除,变成 ⋯ X ✓ X ⋯ \cdots X \checkmark X \cdots ⋯X✓X⋯ 仍然符合描述,但n减少了1。不断迭代n,当n为1时,证明成立。
动态规划的状态表示
pre[b1][b2][k] 表示[0,i)中选取了k个数的最大值,b1是否选择了i-1,b2是否选择了0。
dp类似,表示[0,i+1)的情况。
动态规划的转移方程
当前数 没选择。
b1 变成0。其它不变。
下面分析选取的情况:
b11=true b21=b2 k1=k+1
k的取值范围:[0,n-1)
dp[b11][b21][k1] = max( ⋯ \cdots ⋯,pre[b1][b2][k]+arr[i])
如果b1等于true,忽略。如果i为3n-1,且b2,忽略。
动态规划的初始值
pre[1][1][1] = arr[0]
pre[0][0][0] = 0
其它 -1e6表示非法状态
动态规划的填表顺序
i从1到3n-1
动态规划的返回值
max(dp[0][0].back() + dp[0][1].back(),dp[1][0].back()+dp[1][1].back())
代码
核心代码
class Solution {
public:int maxSizeSlices(vector<int>& slices) {const int n3 = slices.size();const int n = n3 / 3;vector<vector<vector<int>>> pre(2, vector<vector<int>>(2, vector<int>(n + 1, m_iNotMay)));pre[1][1][1] = slices[0];pre[0][0][0] = 0;for (int i = 1; i < n3; i++){vector<vector<vector<int>>> dp(2, vector<vector<int>>(2, vector<int>(n + 1, m_iNotMay)));//不选择slices[i]for (int i2 = 0; i2 < 2; i2++){for (int i3 = 0; i3 <= n; i3++){dp[0][i2][i3] = max(pre[0][i2][i3], pre[1][i2][i3]);}}//选择{for (int i3 = 0; i3 < n; i3++){dp[1][0][i3+1] = max(dp[1][0][i3+1], pre[0][0][i3] + slices[i]);}}if (n3 - 1 != i){for (int i3 = 0; i3 < n; i3++){dp[1][1][i3+1] = max(dp[1][1][i3+1], pre[0][1][i3] + slices[i]);}}pre.swap(dp);}vector<int> vMax = { pre[0][0].back(), pre[0][1].back(),pre[1][0].back(),pre[1][1].back() };return *std::max_element(vMax.begin(), vMax.end());}const int m_iNotMay = -1000'000;
};
测试用例
int main()
{ vector<int> slices;int d;{Solution sln;slices = { 1, 2, 3, 4, 5, 6 };auto res = sln.maxSizeSlices(slices);Assert(10, res);}{Solution sln;slices = { 8,9,8,6,1,1 };auto res = sln.maxSizeSlices(slices);Assert(16, res);}{Solution sln;slices = { 9,5,1,7,8,4,4,5,5,8,7,7 };auto res = sln.maxSizeSlices(slices);Assert(30, res);}{Solution sln;slices = { 10,9,1,10,8,5,10,2,2 };auto res = sln.maxSizeSlices(slices);Assert(30, res);}{Solution sln;slices = { 4,1,2,5,8,3,1,9,7 };auto res = sln.maxSizeSlices(slices);Assert(21, res);}
}优化
关于0和3n-1不能同时选择的解决方法:
情况一:选择了0,没有选择3n-1。
情况二:选择了3n-1,没有选择0。
情况三:两者都没选择。
只处理slices的前3n-1个元素,可以枚举所有的情况一和情况三。
值处理slices的后3n-1个元素,可以枚举所有的情况一和情况三。
class Solution {
public:int maxSizeSlices(vector<int>& slices) {const int n3 = slices.size();const int n = n3 / 3;return max(Do(slices.data(),n3-1,n), Do(slices.data()+1, n3 - 1, n));}int Do(int* slices, int len, int n){vector<vector<int>> pre(2, vector<int>(n + 1, m_iNotMay));pre[0][0] = 0;pre[1][1] = slices[0];for (int i = 1; i < len; i++){vector<vector<int>> dp(2, vector<int>(n + 1, m_iNotMay)); for (int i2 = 0; i2 <= n; i2++){//不选择dp[0][i2] = max(pre[0][i2], pre[1][i2]);}for (int i2 = 0; i2 < n; i2++){dp[1][i2+1] = max(pre[1][i2+1], pre[0][i2]+slices[i]);}pre.swap(dp);}return max(pre[0].back(), pre[1].back());}const int m_iNotMay = -1000'000;
};

2023年2月版
class Solution {
public:
int maxSizeSlices(vector& slices) {
m_c = slices.size();
vector<vector> dp(m_c/3+1,vector(m_c));
{
for (int i = 0; i < m_c; i++)
{
dp[1][i] = slices[GetIndex(i + 1)];
}
}
for (int len = 6; len <= m_c; len += 3)
{
for (int iPos = 0; iPos < m_c; iPos++)
{
int iMaxValue = 0;
//可以拆分2个
for (int j = 3; j < len; j += 3)
{
int iVaue = dp[j/3][iPos] + dp[(len-j) / 3][GetIndex( iPos+j)];
iMaxValue = max(iMaxValue, iVaue);
}
//消除两端元素和中间元素
for (int j = 1; j < len; j+=3 )
{
int iVaue = slices[GetIndex(iPos + j)] + dp[(j - 1) / 3][GetIndex(iPos + 1)];
const int iRightLen = (len - j -2 ) / 3;
if ( iRightLen > 0 )
{
iVaue += dp[iRightLen][GetIndex(iPos + j + 1)];
}
iMaxValue = max(iMaxValue, iVaue);
}
dp[len / 3][iPos] = iMaxValue;
}
}
auto& pre = dp[m_c / 3];
return *std::max_element(pre.begin(), pre.end());
}
int GetIndex(int index)
{
return (index + m_c)%m_c;
}
int m_c;
};
2023年8月版
class Solution {
public:
int maxSizeSlices(vector& slices) {
needSel = slices.size() / 3;
vector<vector<vector>> pre(2, vector<vector>(2, vector(needSel+1, -1000 * 1000)));
pre[0][0][0] = 0; //pre[i][j][k] i是否选择第0个元素,j前一个元素是否被选择,已经选择了多少个
for (int i = 0; i < slices.size(); i++)
{
vector<vector<vector>> dp(2, vector<vector>(2, vector(needSel + 1, -1000 * 1000)));
for (auto sel0 = 0; sel0 < 2; sel0++)
{
for (auto selPre = 0; selPre < 2; selPre++)
{
for (int hasSel = 0; hasSel <= needSel; hasSel++)
{
//不选择
dp[sel0][0][hasSel] = max(dp[sel0][0][hasSel],pre[sel0][selPre][hasSel]);
//选择
bool bCanSel = (hasSel < needSel) && (!selPre);
if (sel0 && (i + 1 == slices.size()))
{
bCanSel = false;
}
if (bCanSel)
{
bool sel0cur = sel0 || (0 == i);
dp[sel0cur][1][hasSel+1] = max(dp[sel0cur][1][hasSel + 1], pre[sel0][selPre][hasSel] + slices[i]);
}
}
}
}
pre.swap(dp);
}
int iMax = 0;
for (auto sel0 = 0; sel0 < 2; sel0++)
{
for (auto selPre = 0; selPre < 2; selPre++)
{
iMax = max(iMax, pre[sel0][selPre].back());
}
}
return iMax;
}
int needSel;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【数学】1388. 3n 块披萨
作者推荐 【动态规划】【字符串】【表达式】2019. 解出数学表达式的学生分数 本文涉及知识点 动态规划汇总 LeetCode1388 3n 块披萨 给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨: 你挑选 任…...
CS144--Chapter0--wsl2+docker环境搭建
我的笔记本配置 荣耀magicbook16,容量是500G,芯片是R7-5800 由于笔记本容量较小,因此考虑这个方案,对于台式机用户,建议可以直接用虚拟机或者双系统。 前言 斯坦福官网给出的方法是用他们的镜像(基于Ubu…...

MGRE实验报告二
实验要求: 实验预览图: 实验分析: 1、对R1-R5配置IP地址,同时R1-R5每个路由器各有一个环回 2.1、对R1、R3、R4路由器开启虚拟接口1,分别配置隧道IP、接口封装协议,接口类型、定义封装源、开启伪广播功能&…...

算法设计与分析实验:最短路径算法
一、网络延迟时间 力扣第743题 本题采用最短路径的思想进行求解 1.1 具体思路 (1)使用邻接表表示有向图:首先,我们可以使用邻接表来表示有向图。邻接表是一种数据结构,用于表示图中顶点的相邻关系。在这个问题中&am…...
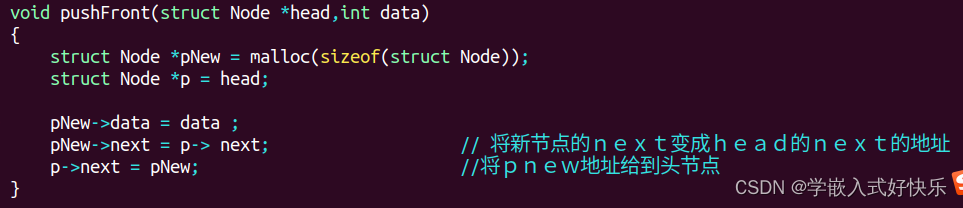
共用体与枚举法,链表的学习
结构体注意事项: 1.结构体类型可以定义在main函数里面,但是此时的作用域就被限定在该函数中 2.结构体的的的定义的形式:a.先定义类型,后定义变量-----struct stu s b.定义类型的同时,定义了变量:struct…...
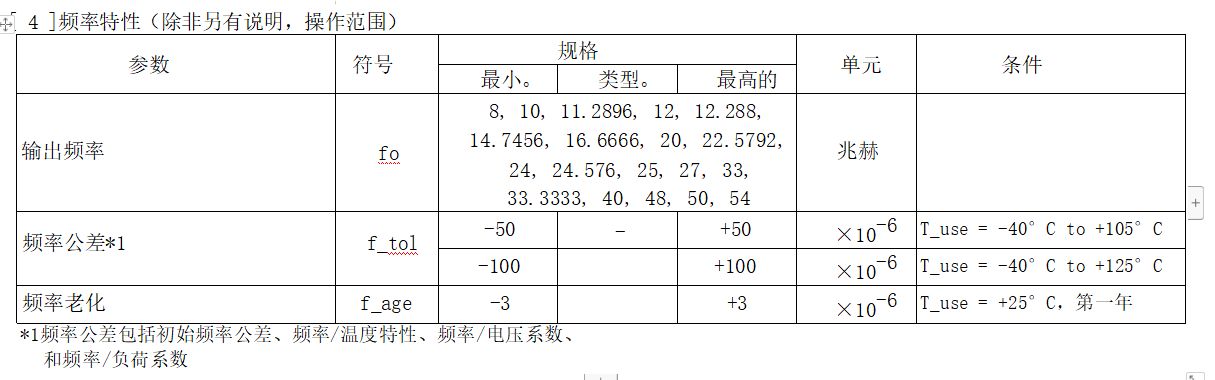
SG2520CAA汽车用晶体振荡器
爱普生SG2520CAA是简单的封装晶体振荡器(SPXO),具有CMOS输出,这款SPXO是汽车和高可靠性应用的理想选择,符合AEC-Q200标准,功耗低,工作电压范围为1.8 V ~ 3.3 V类型,宽工作温度-40℃~…...

使用pip将第三方依赖包下载到本地指定位置
pip download -d save_path packages -d:后面接下载包路径(save_path) packages:安装包名称...
C语言探索:水仙花数的奥秘与计算
摘要: 水仙花数,一种特殊的三位数,其各位数字的立方和等于该数本身。本文将详细介绍水仙花数的定义、性质,以及如何使用C语言来寻找100至999范围内的水仙花数。 目录 一、水仙花数的定义与性质 二、用C语言寻找100至999范围内的…...

2024年人工智能应用与先进制造科学国际学术会议(ICAIAAMS 2024)
2024年人工智能应用与先进制造科学国际学术会议(ICAIAAMS 2024) 2024 International Conference on Artificial Intelligence Applications and Advanced Manufacturing Science (ICAIAAMS 2024) 会议简介: 2024年人工智能应用与先进制造科学国际学术会议ÿ…...
计算机图形学 实验
题目要求 1.1 实验一:图元的生成:直线、圆椭区域填充 你需要完成基本的图元生成算法,包括直线和椭圆。 在区域填充中,要求你对一个封闭图形进行填充。你需要绘制一个封 闭图形(例如多边形),并选…...

React + react-device-detect 实现设备特定的渲染
当构建响应式网页应用时,了解用户正在使用的设备类型(如手机、平板或桌面)可以帮助我们提供更优化的用户体验。本文将介绍如何在 React 项目中使用 react-device-detect 库来检测设备类型,并根据不同的设备显示不同的组件或样式。…...
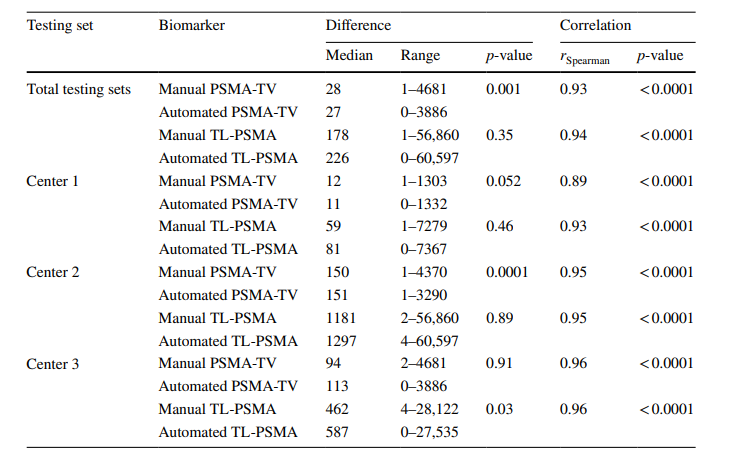
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割 01 文献速递介绍 前列腺特异性膜抗原(PSMA)PET/CT成像近年来在前列腺癌检测领域中获得了显著的重视。PSMA是一种在前列腺上皮…...
2024 IC FPGA 岗位 校招面试记录
引言 各位看到这篇文章时,24届校招招聘已经渐进尾声了。 在这里记录一下自己所有面试(除了时间过短或者没啥干货的一些研究所外,如中电55所(南京),航天804所(上海))的经…...

Linux 命令 —— top
Linux 命令 —— top 相对于 ps 是选取一个时间点的进程状态,top 则可以持续检测进程运行的状态。使用方式如下: 用法: top [-d secs] | [-p pid] 选项与参数: -d secs:整个进程界面更新 secs 秒。默认是 5 5 5 秒。…...

【Docker】使用VS创建、运行、打包、部署.net core 6.0 webapi
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...
抖音短视频矩阵营销系统源头独立开发搭建
开发背景 抖音短视频矩阵系统源码开发采用模块化设计,包括账号分析、营销活动、数据监控、自动化管理等功能。通过综合分析账号数据,快速发现账号的优势和不足,并提供全面的营销方案,以提高账号曝光率和粉丝数量。同时,…...
Springboot使用数据库连接池druid
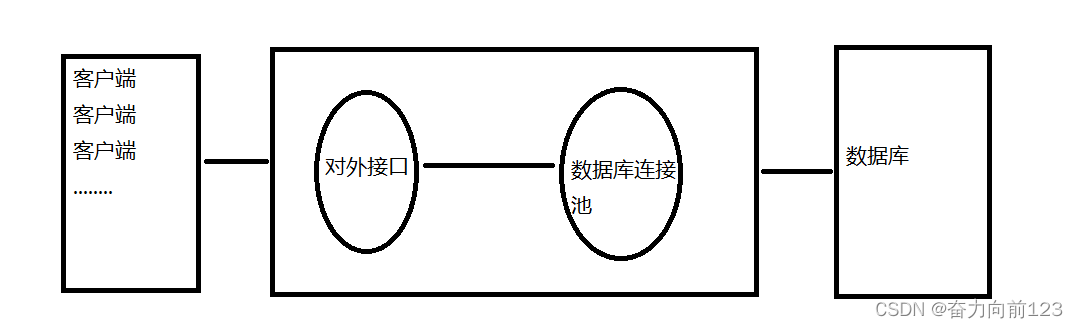
springboot框架中可以使用druid进行数据库连接池,下面介绍druid在springboot中使用和参数配置介绍。 数据库连接池(Druid)是一种用于管理数据库连接的机制,其工作原理和常见使用方法如下: 原理:数据库连接…...

Springboot-前后端分离——第三篇(三层架构与控制反转(IOC)-依赖注入(DI)的学习)
本篇主要对ControllerServiceDAO三层结构以及控制反转(IOC)与DI(依赖注入)进行总结。 目录 一、三层架构: Controller/Service/DAO简介: 二、控制反转(IOC)-依赖注入(DI): 概念介绍: DOC与…...
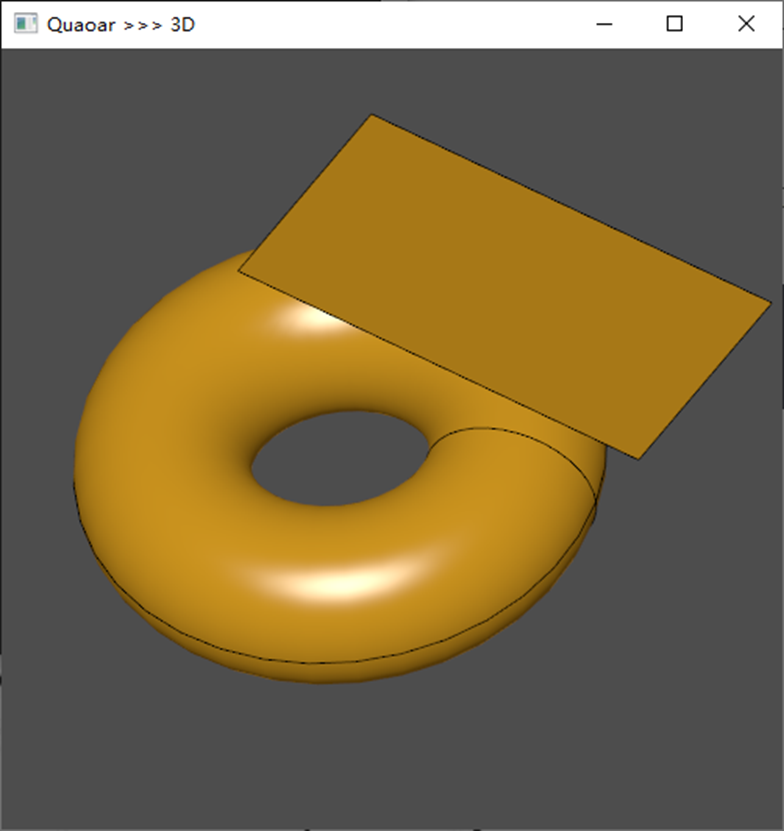
Open CASCADE学习|曲面上一点的曲率及切平面
曲率(Curvature)是一个几何学的概念,用于描述一个物体的形状在某一点上的弯曲程度。在我们日常生活中,曲率与我们的生活息息相关,如道路的弯道、建筑物的拱形结构、自然界的山脉等等。了解曲率的概念和计算方法&#x…...
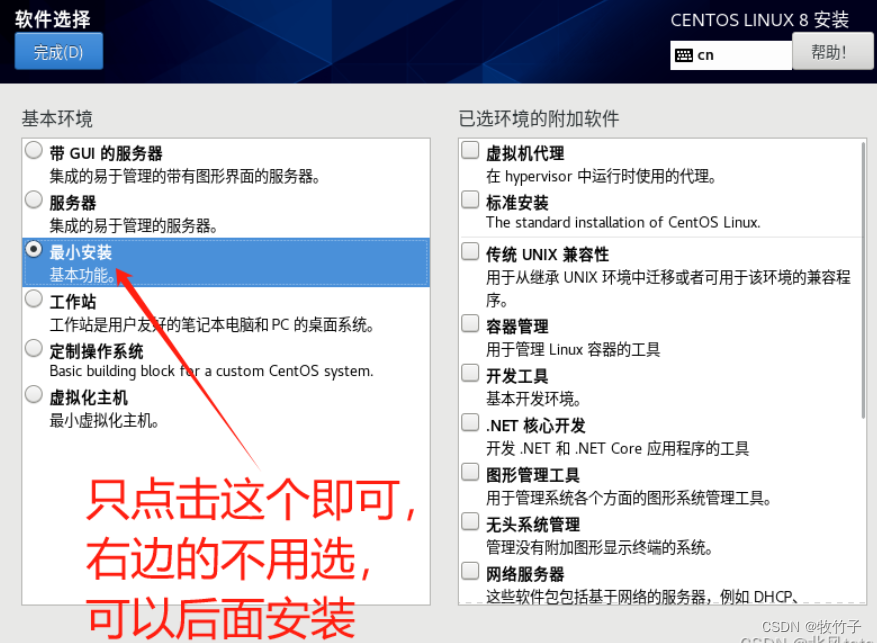
CentOS 8最小安装和网络配置
文章目录 简介下载地址VMware 17创建虚拟机最小化安装拥有的外部命令yum源有问题网络配置开启SSH Server服务关闭防火墙设置host配置JDK环境完整参考 简介 CentOS 8的IOS如果下载DVD版本至少有10G 这里我们直接选择最小安装,因此选择最小系统boot版本 CentOS-8.5.21…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
