当前位置： 首页 > news >正文

第8章 SpringBoot任务管理

news 2026/2/10 4:39:49

学习目标

  • 熟悉SpringBoot整合异步任务的实现

  • 熟悉SpringBoot整合定时任务的实现

  • 熟悉SpringBoot整合邮件任务的实现

开发web应用时，多数应用都具备任务调度功能。常见的任务包括异步任务，定时任务和发邮件任务。我们以数据库报表为例看看任务调度如何帮助改善系统设计。报表可能时错综复杂的，用户可能需要很长时间找到需要的报表数据，此时，我们可以在这个报表应用中添加异步任务减少用户等待时间，从而提高用户体验，除此之外，还可以在报表应用中添加定时任务和邮件任务，以便用户可以安排在任何它们需要的时间定时生成报表，并在Email中发送。

8.1 异步任务

web应用开发中，大多数情况都是通过同步方式完成数据交互处理，但是，当处理与第三方系统的交互时，容易造成响应迟缓的情况，之前大部分都是使用多线程完成此类任务，除此之外，还可以使用异步调用的方式完美解决这个问题。根据异步处理方式的不同，可以将异步任务的调用分为无返回值异步任务调用和有返回值异步任务调用。

8.1.1 无返回值异步任务调用

在实际开发中，项目可能会向新注册用户发送短信验证码，这时，可以考虑使用异步任务调用的方式实现，一方面时因为用户对这个时效性要求不是特别高，另一方面在特定时间范围内没有收到验证码，用户可以点击再次发送验证码。

1.SpringBoot项目创建

使用Spring Initializr框架提供了对异步任务的支持，SpringBoot框架继承了这一异步任务功能。在SpringBoot中整合异步任务时，只需在项目中引入web模块中的web依赖就可以

相关文章：

第8章 SpringBoot任务管理

学习目标 熟悉SpringBoot整合异步任务的实现 熟悉SpringBoot整合定时任务的实现 熟悉SpringBoot整合邮件任务的实现 开发web应用时，多数应用都具备任务调度功能。常见的任务包括异步任务，定时任务和发邮件任务。我们以数据库报表为例看看任务调度如何帮助改善系统设计。报表可…...

编程日记 2024/2/3 1:55:52

Qt5 基于OpenGL实现六轴机械臂三维仿真

需求 在Qt中通过OPenGL方式加载三维模型STL文件，然后将多个结构的STL文件类型的模型进行组装，形成6轴机械臂三维模型的显示，并且可以对每个关节进行关节角度的控制。 新建一个C类STLFileLoader，用于加载STL文件，并进…...

编程日记 2024/2/3 1:54:50

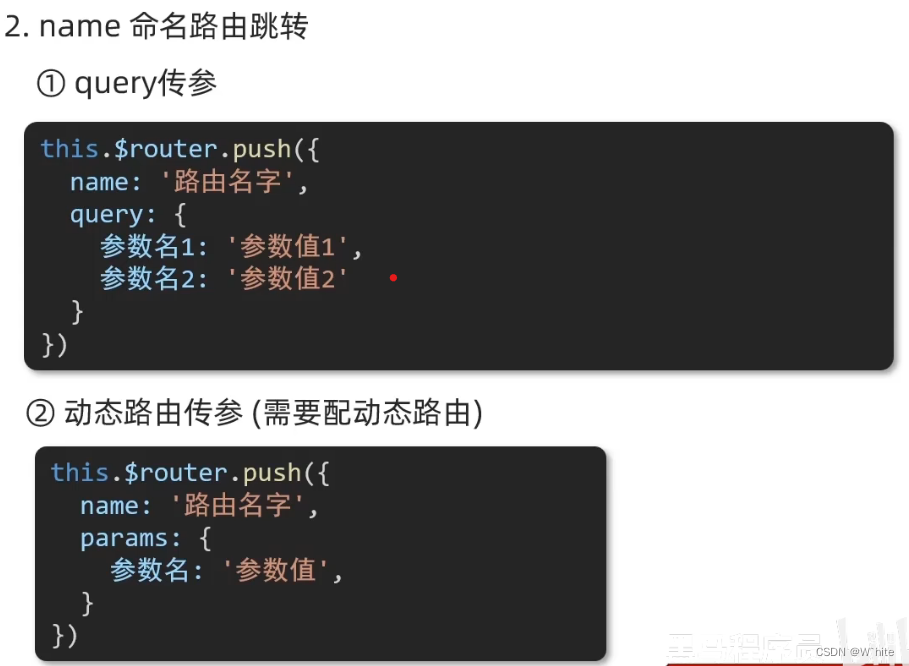
路由进阶

文章目录 1.路由的封装抽离2.声明式导航 - 导航链接3.声明式导航-两个类名自定义匹配的类名 4.声明式导航 - 跳转传参查询参数传参动态路传参两种传参方式的区别动态路由参数可选符 5.Vue路由 - 重定向6.Vue路由 - 4047.Vue路由 - 模式设置8.编程式导航 - 两种路由跳转9.编程式…...

编程日记 2024/2/3 1:53:49

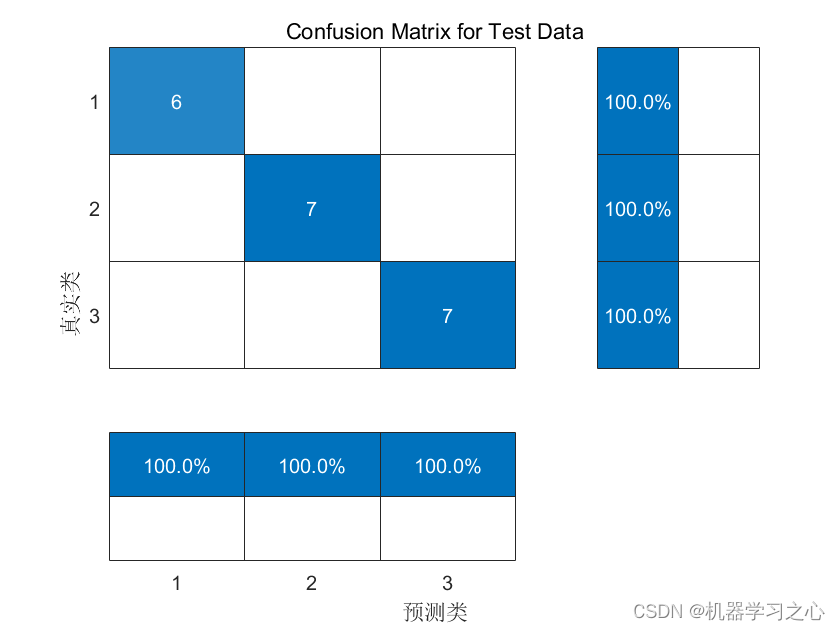
分类预测 | Matlab实现SCN-Adaboost随机配置网络模型SCN的Adaboost数据分类预测/故障识别

分类预测 | Matlab实现SCN-Adaboost随机配置网络模型SCN的Adaboost数据分类预测/故障识别 目录 分类预测 | Matlab实现SCN-Adaboost随机配置网络模型SCN的Adaboost数据分类预测/故障识别分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现SCN-Adaboost随机配置网…...

编程日记 2024/2/3 1:52:48

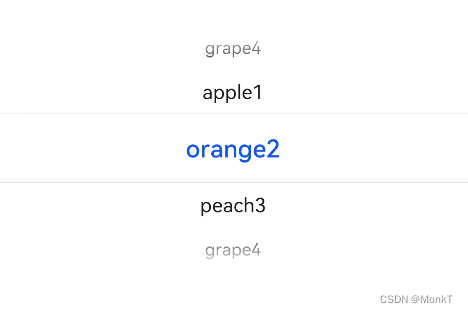
鸿蒙（HarmonyOS）项目方舟框架（ArkUI）之TextPicker组件

鸿蒙（HarmonyOS）项目方舟框架（ArkUI）之TextPicker组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、TextPicker组件 TextClock组件通过文本将当前系统时间显示在设备上。支持不…...

编程日记 2024/2/3 1:50:46

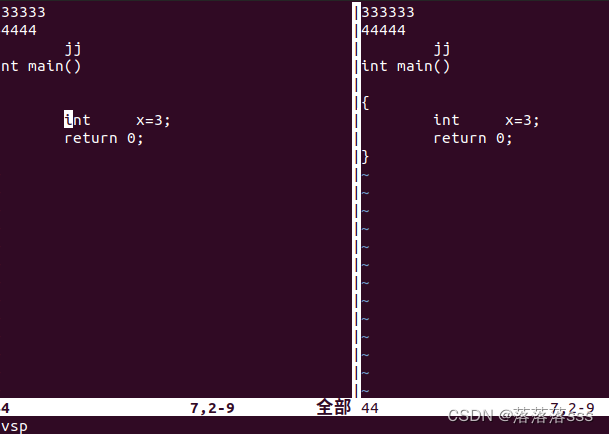
linux中vim的操作

(码字不易，关注一下吧w~~w) 命令模式： 当我们按下esc键时，我们会进入命令模式；当使用vi打开一个文件时也是进入命令模式。 光标移动： 1 保存退出：ZZ 2 代码格式化：ggG 3 光标移动&#xff…...

编程日记 2024/2/3 1:44:40

《统计学习方法：李航》笔记 从原理到实现（基于python）-- 第5章 决策树

文章目录 第5章 决策树5.1 决策树模型与学习5.1.1 决策树模型5.1.2 决策树与if-then规则5.1.3 决策树与条件概率分布5.1.4 决策树学习5.2 特征选择5.2.1 特征选择问题5.2.2 信息增益5.2.3 信息增益比5.3.1 ID3算法5.3.2 C4.5的生成算法5.4 决策树的剪枝5.5 CART算法5.5.1 CART生…...

编程日记 2024/2/3 1:41:38

【C++11(一)】列表初始化and右值引用

一、 统一的列表初始化 1.1 ｛｝初始化 在C98中，标准允许 使用花括号{}对数组或者结构体元素 进行统一的列表初始值设定 C11扩大了用大括号 括起的列表(初始化列表)的使用范围 使其可用于所有的内置类型和 用户自定义的类型 使用初始化列表时…...

编程日记 2024/2/3 1:37:34

为什么SSL会握手失败？SSL握手失败原因及解决方案

随着网络安全技术的发展，SSL证书作为网站数据安全的第一道防线，被越来越多的企业选择。SSL证书使用的是SSL协议，而SSL握手是SSL协议当中最重要的一部分。当部署SSL证书时，如果服务器和客户端之间无法建立安全连接，就会…...

编程日记 2024/2/3 1:35:33

STM32——智能小车

STM32——智能小车 硬件接线 B-1A – PB0 B-1B – PB1 A-1A – PB2 A-1B – PB10 其余接线参考51单片机小车项目。 1.让小车动起来 motor.c #include "motor.h" void goForward(void) {// 左轮HAL_GPIO_WritePin(GPIOB, GPIO_PIN_2, GPIO_PIN_SET);HAL_GPIO…...

编程日记 2024/2/3 1:32:30

开源：基于Vue3.3 + TS + Vant4 + Vite5 + Pinia + ViewPort适配..搭建的H5移动端开发模板

vue3.3-Mobile-template 基于Vue3.3 TS Vant4 Vite5 Pinia ViewPort适配 Sass Axios封装 vconsole调试工具，搭建的H5移动端开发模板，开箱即用的。 环境要求： Node:16.20.1 pnpm:8.14.0 必须装上安装pnpm，没装的看这篇…...

编程日记 2024/2/3 1:31:29

缩略图保持加密(thumbnail-preserving encryption, TPE)的理论基础

这涉及到一些视觉心理学等方面知识： 1、参考文献： 云存储图像缩略图保持的加密研究进展（中国图像图形学报） 一些视觉心理学的研究为TPE的成功实现提供了理论基础。Potter(1975, 1976)的研究表明人类的视觉系统能够在100 ms内从一个新场景中提取出相应的语义信息；250 ms内…...

编程日记 2024/2/3 1:29:26

nodejs+vue+mysql校园失物招领网站38tp1

本高校失物招领平台是为了提高用户查阅信息的效率和管理人员管理信息的工作效率，可以快速存储大量数据，还有信息检索功能，这大大的满足了用户和管理员这两者的需求。操作简单易懂，合理分析各个模块的功能，尽可能优化界…...

编程日记 2024/2/3 1:28:23

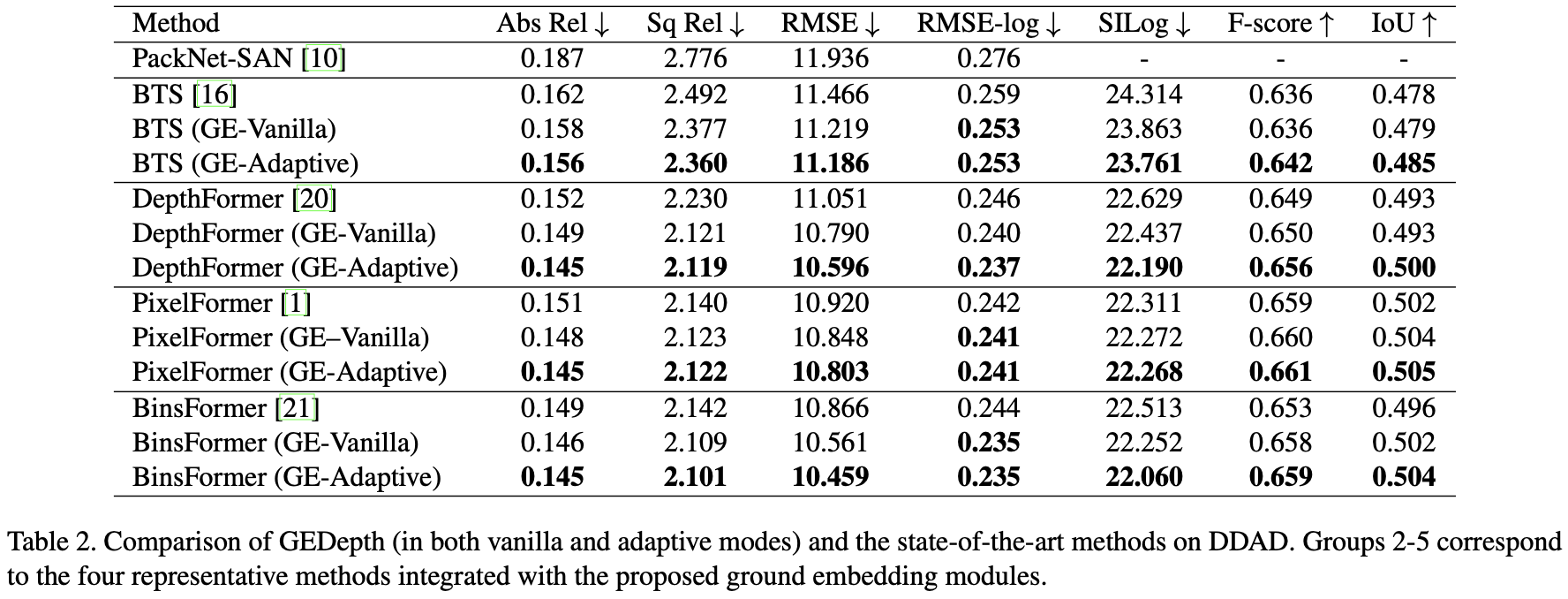
GEDepth：Ground Embedding for Monocular Depth Estimation

参考代码：gedepth 出发点与动机 相机的外参告诉了相机在世界坐标系下的位置信息，那么可以用这个外参构建一个地面基础深度作为先验，后续只需要在这个地面基础深度先验基础上添加offset就可以得到结果深度，这样可以极大简化深度估…...

编程日记 2024/2/3 1:27:23

校园圈子论坛系统--APP小程序H5，前后端源码交付，支持二开！uniAPP+PHP书写！

随着移动互联网的快速发展，校园社交成为了大学生们日常生活中重要的一部分。为了方便校园内学生的交流和互动，校园社交小程序逐渐走入人们的视野。本文将探讨校园社交小程序的开发以及其带来的益处。 校园社交小程序的开发涉及许多技术和设计方面。首先&…...

编程日记 2024/2/3 1:26:22

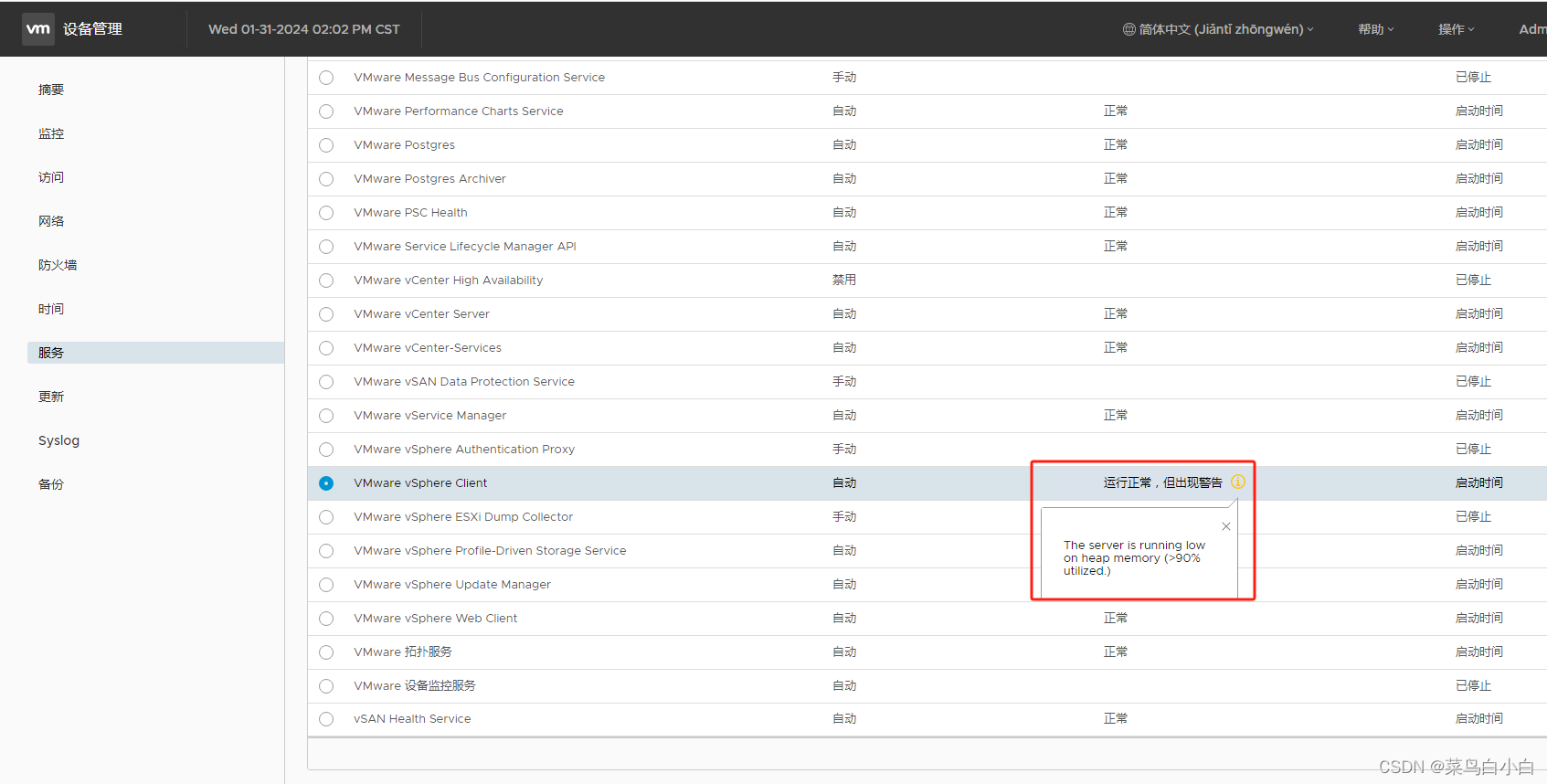
VMware vCenter告警：vSphere UI运行状况警报

vSphere UI运行状况警报 不会详细显示告警的具体内容，需要我们自己进一步确认告警原因。 vSphere UI运行状况警报是一种监控工具，用于检测vSphere环境中的潜在问题。当警报触发时，通常表示系统遇到了影响性能或可用性的问题。解决vSphere UI…...

编程日记 2024/2/3 1:24:20

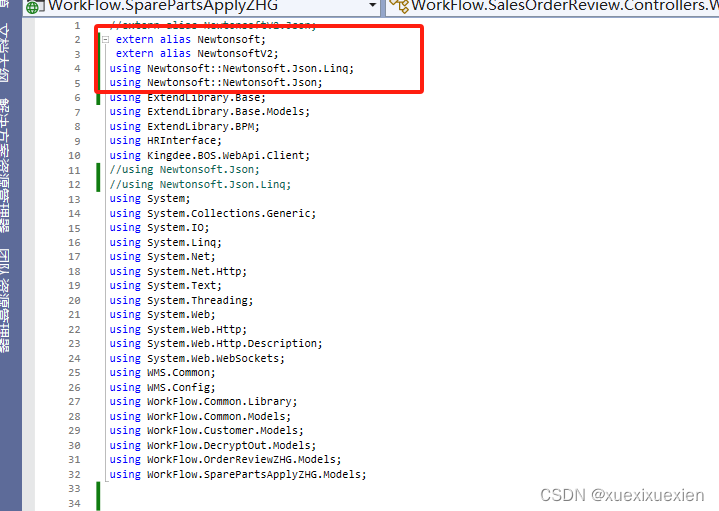
C# 引用同一个dll不同版本的程序集

因为项目需要所以必须在项目中引用不同版本的同一程序集 我要引用的文件是newtonsoft.json.dll 两个版本为12.0.0.0 和4.0.0.0 1.如果已经先引入了newtonsoft.json 12.0.0.0版本的程序集，如果直接引入另一个版本的程序集的话会提示不成功，所以先将另一个…...

编程日记 2024/2/3 1:22:19

单机搭建hadoop环境（包括hdfs、yarn、hive）

单机可以搭建伪分布式hadoop环境，用来测试和开发使用，hadoop包括： hdfs服务器 yarn服务器，yarn的前提是hdfs服务器， 在前面两个的基础上，课可以搭建hive服务器，不过hive不属于hadoop的必须部…...

编程日记 2024/2/3 1:20:16

LEETCODE 170. 交易逆序对的总数

class Solution { public:int reversePairs(vector<int>& record) {if(record.size()<1)return 0;//归并 递归int left,right;left0;rightrecord.size()-1;int nummergeSort(left,right,record);return num;}int mergeSort(int left,int right, vector<int>…...

编程日记 2024/2/3 1:19:15

「HarmonyOS」EventHub事件通知详细使用方法

需求背景&#xff1a; 在开发过程中&#xff0c;肯定会出现触发特定事件&#xff0c;需要全局进行通知&#xff0c;与之相关的部分进行执行相应的修改方法。举个例子&#xff1a;修改了用户个人昵称&#xff0c;需要进行全局通知&#xff0c;在涉及昵称的部分收到通知后&#…...

编程日记 2024/2/3 1:17:13

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

线程与协程

1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指&#xff1a;像函数调用/返回一样轻量地完成任务切换。 举例说明&#xff1a; 当你在程序中写一个函数调用&#xff1a; funcA() 然后 funcA 执行完后返回&…...

编程新知 2025/10/31 17:25:40

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36

2023赣州旅游投资集团

单选题 1.“不登高山&#xff0c;不知天之高也&#xff1b;不临深溪&#xff0c;不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

编程新知 2025/11/8 16:42:13

LeetCode - 199. 二叉树的右视图

题目 199. 二叉树的右视图 - 力扣&#xff08;LeetCode&#xff09; 思路 右视图是指从树的右侧看&#xff0c;对于每一层&#xff0c;只能看到该层最右边的节点。实现思路是&#xff1a; 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

编程新知 2025/9/13 20:07:18

STM32---外部32.768K晶振（LSE）无法起振问题

晶振是否起振主要就检查两个1、晶振与MCU是否兼容&#xff1b;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容&#xff08;CL&#xff09;与匹配电容&#xff08;CL1、CL2&#xff09;的关系 2. 如何选择 CL1 和 CL…...

编程新知 2026/2/7 10:55:43

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分&#xff1a; 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

编程新知 2025/8/27 0:09:05

springboot 日志类切面，接口成功记录日志，失败不记录

springboot 日志类切面&#xff0c;接口成功记录日志&#xff0c;失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

编程新知 2026/2/1 13:59:09