蚁群算法优化最优值
%%%%%%%%%%%%%%蚁群算法求函数极值%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m = 20; %蚂蚁个数
G = 500; %最大迭代次数
Rho = 0.9; %信息素蒸发系数
P0 = 0.2; %转移概率常数
XMAX = 5; %搜索变量 x 最大值
XMIN = -5; %搜索变量 x 最小值
YMAX = 5; %搜索变量 y 最大值
YMIN = -5; %搜索变量 y 最小值
%%%%%%%%%%%%%随机设置蚂蚁初始位置%%%%%%%%%%%%%%%%
for i = 1:m
X(i,1) = (XMIN+(XMAX-XMIN)*rand);
X(i,2) = (YMIN+(YMAX-YMIN)*rand);
Tau(i) = func(X(i,1),X(i,2));
end
step = 0.1; %局部搜索步长
for NC = 1:G
lamda = 1/NC;
[Tau_best,BestIndex] = min(Tau);
%%%%%%%%%%%%%计算状态转移概率%%%%%%%%%%%%%%%
for i = 1:m
P(NC,i) = (Tau(BestIndex)-Tau(i))/Tau(BestIndex);
end
%%%%%%%%%%%%%%%%位置更新%%%%%%%%%%%%%%%%%
for i = 1:m
%%%%%%%%%%%%局部搜索%%%%%%%%%%%%%%%%%
if P(NC,i) < P0
temp1 = X(i,1)+(2*rand-1)*step*lamda;
temp2 = X(i,2)+(2*rand-1)*step*lamda;
else
%%%%%%%%%%%%全局搜索%%%%%%%%%%%%%%%%
temp1 = X(i,1)+(XMAX-XMIN)*(rand-0.5);
temp2 = X(i,2)+(YMAX-YMIN)*(rand-0.5);
end
%%%%%%%%%%%%%%%%边界处理%%%%%%%%%%%%%%%
if temp1 < XMIN
temp1 = XMIN;
end
if temp1 > XMAX
temp1 = XMAX;
end
if temp2 < YMIN
temp2 = YMIN;
end
if temp2 > YMAX
temp2 = YMAX;
end
%%%%%%%%%%%%%%%判断蚂蚁是否移动%%%%%%%%%%%
if func(temp1,temp2) < func(X(i,1),X(i,2))
X(i,1) = temp1;
X(i,2) = temp2;
end
end
%%%%%%%%%%%%%%%%%更新信息素%%%%%%%%%%%%%%%
for i = 1:m
Tau(i) = (1-Rho)*Tau(i)+func(X(i,1),X(i,2));
end
[value,index] = min(Tau);
trace(NC) = func(X(index,1),X(index,2));
end
[min_value,min_index] = min(Tau);
minX = X(min_index,1); %最优变量
minY = X(min_index,2); %最优变量
minValue = func(X(min_index,1),X(min_index,2)); %最优值
figure
plot(trace)
xlabel('搜索次数');
ylabel('适应度值');
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%
function value = func(x,y)
value = 20*(x^2-y^2)^2-(1-y)^2-3*(1+y)^2+0.3;
end
相关文章:

蚁群算法优化最优值
%%%%%%%%%%%%%%蚁群算法求函数极值%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 20; %蚂蚁个数 G 500; %最大迭代次数 Rho 0.9; %信息素蒸发系数 P0 0.2; %转移概率常数 XMAX 5; %搜索变量 x…...

Docker镜像的内部机制
Docker镜像的内部机制 镜像就是一个打包文件,里面包含了应用程序还有它运行所依赖的环境,例如文件系统、环境变量、配置参数等等。 环境变量、配置参数这些东西还是比较简单的,随便用一个 manifest 清单就可以管理,真正麻烦的是文…...
每日的时间安排规划
14:23 2023年3月4日星期六 开始 现在我要做一套试卷。模拟6级考试。 现在是: 16:22 2023年3月4日星期六。 做完了线上的试卷! 发现我真的是不太聪明的样子! 明明买的有历年真题,做真题就行了,还要做它们出的模拟的…...
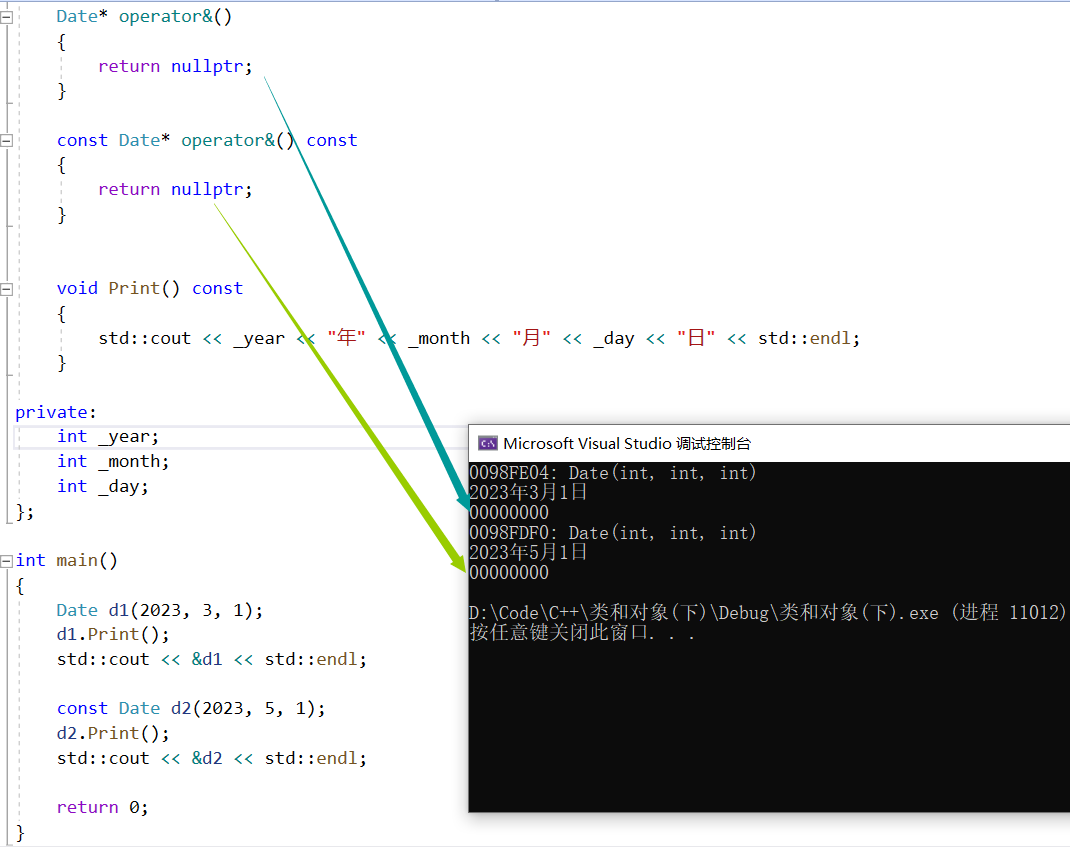
【C++】类和对象——六大默认成员函数
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、类的6个默认成员函数二、构造…...

远程debug被arthas watch了的idea
开发工具idea端(2021.2.1) 远程调试 被 应用了 修改的arthas端 的 鸡idea端(2022.3.2) A. 鸡idea端 鸡idea: “D:\IntelliJ IDEA 2022.3.2\bin\idea64.exe” 中安装有目标插件 比如 RedisNew-2022.07.24.zip 对文件 “D:\IntelliJ IDEA 2022.3.2\bin\idea64.exe.vmoptions” 新…...
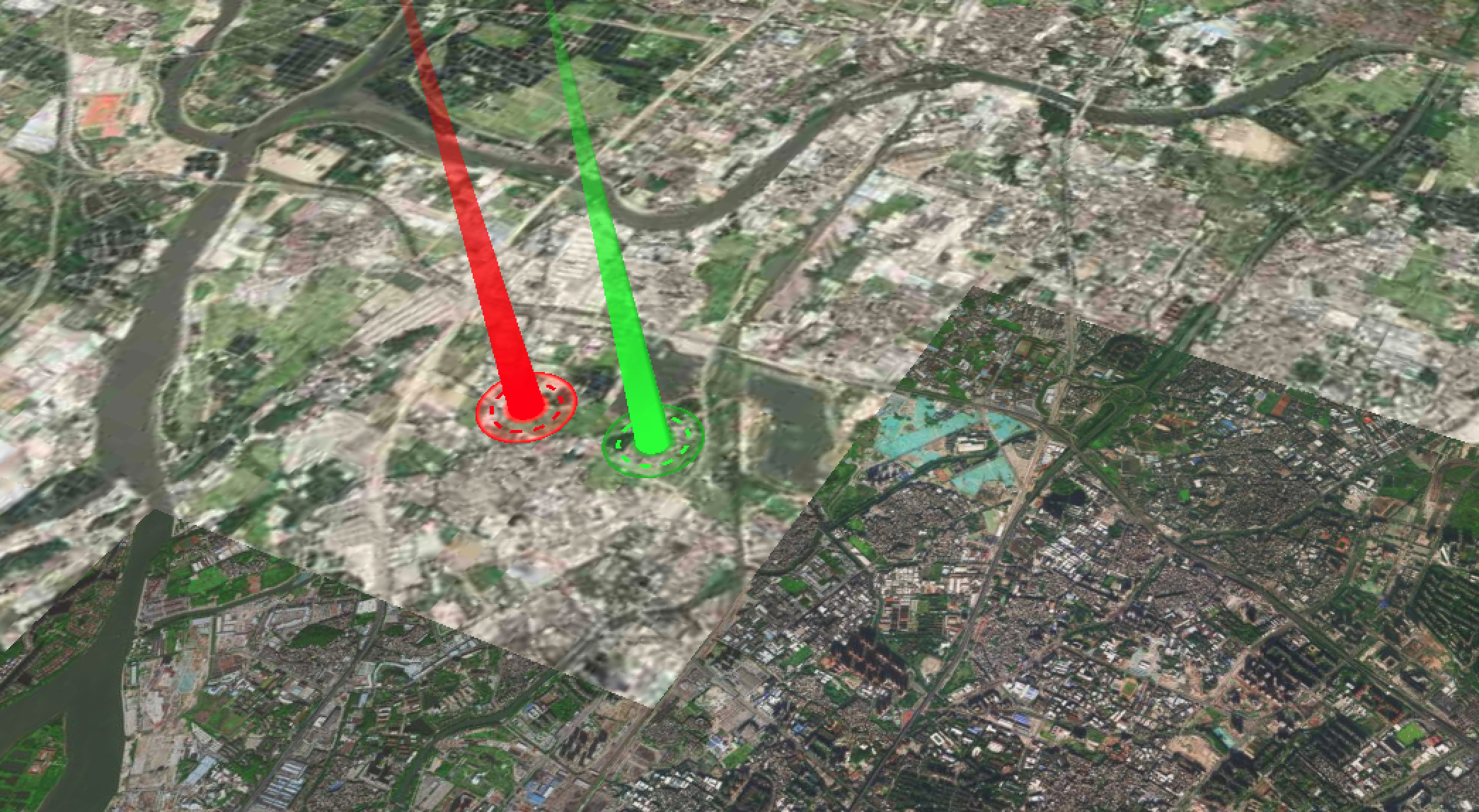
Cesium实现的光柱效果
Cesium实现的光柱效果 效果展示: 可以通过拼接两个entity来实现这个效果: 全部代码; index.html <!DOCTYPE html> <html><head><meta charset...
和splice())
你最爱记混的slice()和splice()
slice()方法:选取数组的一部分,并返回一个新数组 该方法不会改变原始数组,而是将截取到的元素封装到一个新数组中返回 语法:array.slice(start,end),参数的介绍如下: 语法:array.slice(start,end),参数的介绍如下: 1.start:截取开始的位置的索引,包含开始索引 2.…...

【LeetCode】剑指 Offer(15)
目录 题目:剑指 Offer 32 - II. 从上到下打印二叉树 II - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 32 - III. 从上到下打…...

【刷题笔记】之二分查找(搜索插入位置。在排序数组中查找元素的第一个和最后一个位置、x的平方根、有效的完全平方数)
1. 二分查找题目链接 704. 二分查找 - 力扣(LeetCode)给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -…...
)
一起Talk Android吧(第五百一十五回:绘制向外扩散的水波纹)
文章目录整体思路实现方法示例代码各位看官们大家好,上一回中咱们说的例子是"Java中的进制转换",这一回中咱们说的例子是"绘制向外扩散的水波纹"。闲话休提,言归正转, 让我们一起Talk Android吧! 整体思路 …...

基于粒子群改进的支持向量机SVM的情感分类识别,pso-svm情感分类识别
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的情感分类预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型…...
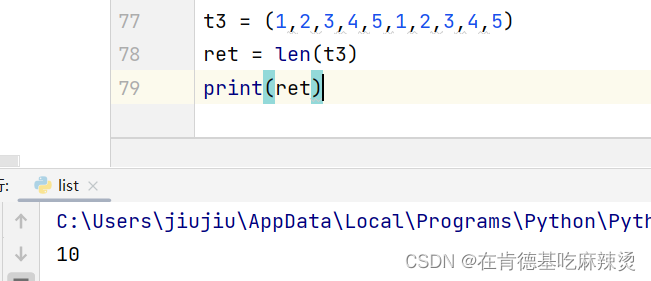
【python中的列表和元组】
文章目录前言一、列表及其使用1.列表的特点2. 列表的使用方法二、元组及其特点1.元组的类型是tuple1.元组的查找操作2. 计算元组某个元素出现的次数3.统计元组内元素的个数总结前言 本文着重介绍python中的列表和元组以及列表和元组之间的区别 一、列表及其使用 1.列表的特点…...

世界顶级五大女程序媛,不仅技术强还都是美女
文章目录1.计算机程序创始人:勒芙蕾丝伯爵夫人2.首位获得图灵奖的女性:法兰艾伦3.谷歌经典首页守护神:玛丽莎梅耶尔4.COBOL之母:葛丽丝穆雷霍普5.史上最强游戏程序媛-余国荔说起程序员的话,人们想到的都会是哪些理工科…...
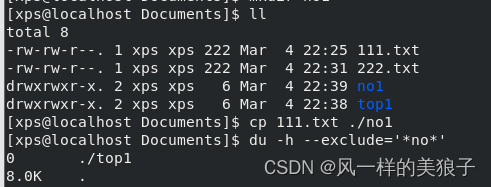
Linux- 系统随你玩之--文件管理-双生姐妹花
文章目录1、前言2、文件管理-双生姐妹花2.1、 df2.1.1、 df 语法2.1.1 、常用参数2.2、 du2.2.1、du 语法2.1.1、 常用参数2.3、双生姐妹花区别2.3.1、 查看文件统计 的计算方式不同2.3.2 、删除文件情况下统计结果 不同2.3.3 、针对双生姐妹花区别 结语3、双生姐妹花实操3.1 、…...
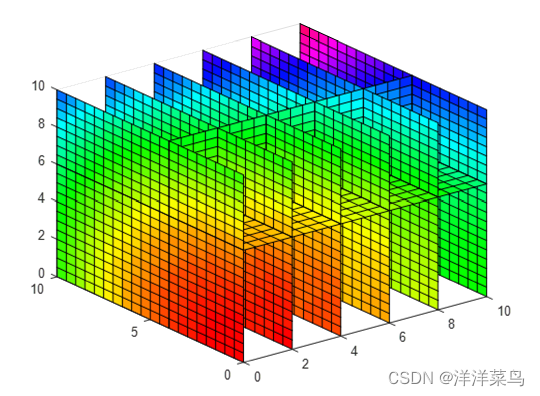
18、多维图形绘制
目录 一、三维图形绘制 (一)曲线图绘制plot3() (二)网格图绘制 mesh() (三)曲面图绘制 surf() (四)光照模型 surfl() (五)等值线图(等高线图)绘制 cont…...
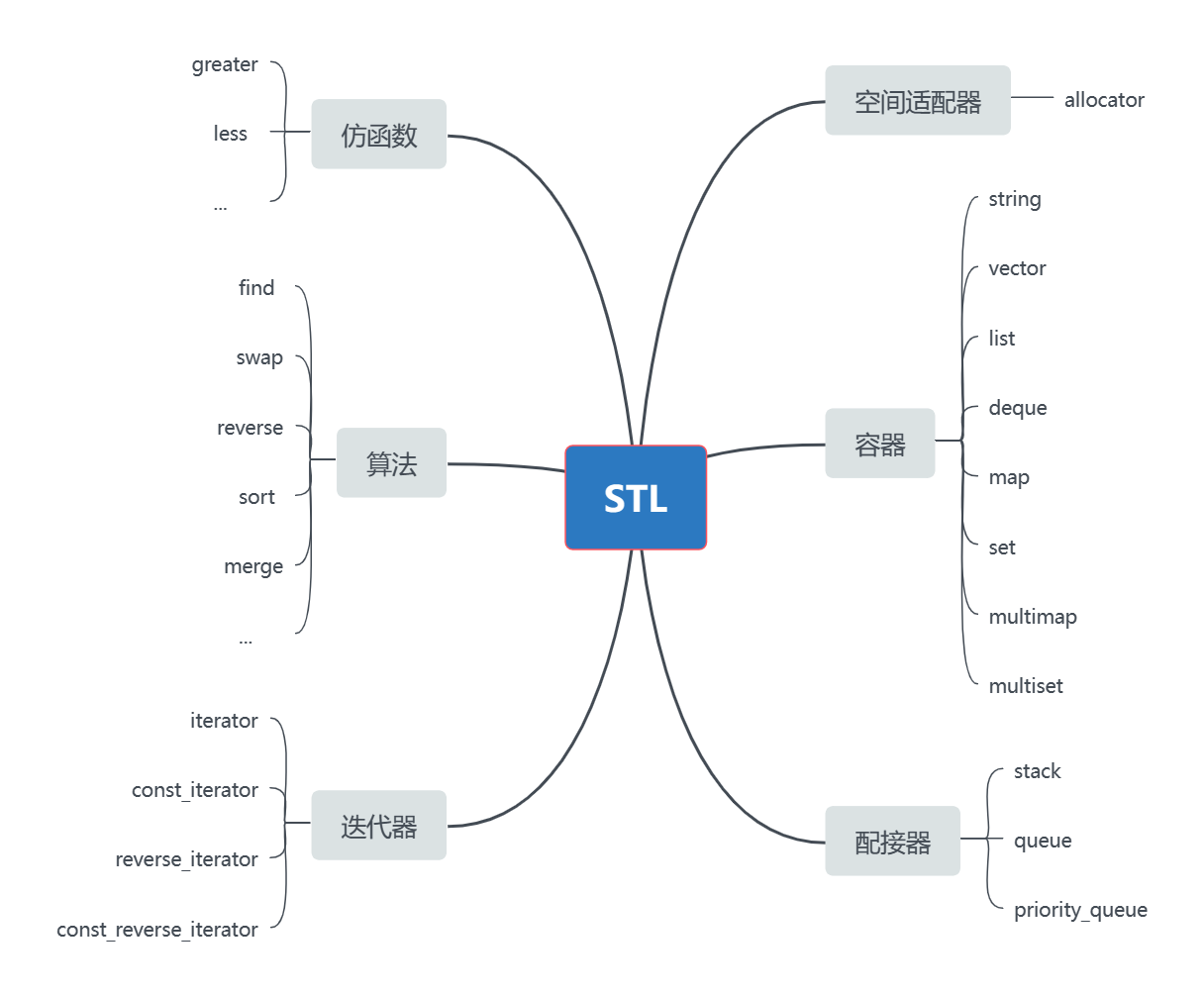
【C++】30h速成C++从入门到精通(STL介绍、string类)
STL简介什么是STLSTL(standard template libaray-标准模板库):是C标准库的重要组成部分,不仅是一个可复用的组件库,而且是一个包罗数据结构与算法的软件框架。STL的版本原始版本Alexander Stepanov、Meng Lee 在惠普实验室完成的原始版本&…...

PMP是什么意思?适合哪些人学呢?
PMP简而言之,就是提高项目管理理论基础和实践能力的考试。 官方一点的说明呢,就是:PMP证书全称为Project Management Professional,也叫项目管理专业人士资格认证。 PMP证书由美国项目管理协会(PMI)发起,是严格评估项…...

【SpringBoot 事务不回滚?怎么解决?】
SpringBoot 事务不回滚可能有多种原因,下面列举一些常见的原因和对应的解决方法: 异常被捕获处理了 如果方法中抛出了异常,但是在方法中被捕获并处理了,那么事务不会回滚。解决方法是让异常继续抛出,或者使用 Transa…...

软件研发管理经验总结 - 技术管理
软件研发管理经验总结 - 技术管理 技术管理主要负责有技术团队建设、管理团队成员技术相关事务、帮助团队成员成长、负责团队成员交付的代码质量、以及负责产品技术方向、以及产品相关前沿技术调研;管理团队成员技术相关事务有代码Review、故障率跟踪、分析及根据分…...

项目实战典型案例19——临时解决方案和最终解决方案
临时解决方案和最终解决方案一:背景介绍二:思路&方案四:总结五:升华一:背景介绍 本篇博客是对项目开发中出现的临时解决方案和最终解决方案进行的总结和改进。目的是将经历转变为自己的经验。通过博客的方式分享给…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
