从编程中理解:大脑中的杏仁核
编程和神经科学在某种程度上可以相互借鉴,尤其是在模拟大脑功能时。让我们以Unity游戏引擎中的C#代码为例,结合金庸武侠小说中的人物形象来构建一个类比故事,探讨如何通过编程模拟大脑中杏仁核的作用。
假设在一款名为“脑海江湖”的Unity游戏中,主角张无忌(代指玩家角色)拥有一个仿生神经系统,其中的“杏仁核模块”负责处理恐惧、愤怒等情绪反应。下面是一个简化的C#实现框架:
using UnityEngine;
using System.Collections;public class BrainEmotionController : MonoBehaviour
{// 张无忌的大脑结构,包含杏仁核组件public Amygdala amygdala;// 情境事件类,代表可能触发情绪反应的情况public class EventStimulus{public string description; // 事件描述public EmotionType emotionType; // 触发的情绪类型}void Update(){// 检查周围环境,获取情境刺激var stimuli = CheckForEventStimuli();foreach (var stimulus in stimuli){HandleStimulus(stimulus);}}List<EventStimulus> CheckForEventStimuli(){// 简化表示,实际应为复杂的环境感知逻辑var stimuli = new List<EventStimulus>();相关文章:

从编程中理解:大脑中的杏仁核
编程和神经科学在某种程度上可以相互借鉴,尤其是在模拟大脑功能时。让我们以Unity游戏引擎中的C#代码为例,结合金庸武侠小说中的人物形象来构建一个类比故事,探讨如何通过编程模拟大脑中杏仁核的作用。 假设在一款名为“脑海江湖”的Unity游戏中,主角张无忌(代指玩家角色…...
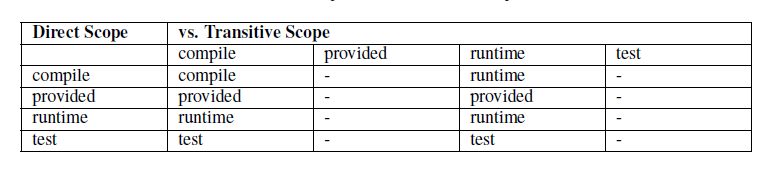
Maven dependency中的scope
Maven的一个哲学是惯例优于配置(Convention Over Configuration), Maven默认的依赖配置项中,scope的默认值是compile。 scope的分类 compile(默认) 含义: compile 是默认值,如果没有指定 scope 值,该元素…...

代码随想录算法训练营DAY11 | 栈与队列 (2)
一、LeetCode 20 有效的括号 题目链接:20.有效的括号https://leetcode.cn/problems/valid-parentheses/ 思路:遇到左括号直接进栈;遇到右括号判断站顶是否有匹配的括号,没有就返回flase,有就将栈顶元素出栈࿱…...

【Spring实战】33 Spring Boot3 集成 Nacos 配置中心
文章目录 1. 配置中心定义2. 解决哪些问题3. 常用的配置中心4. 使用示例1)没引入 Nacos 配置中心2)引入依赖3)配置Nacos连接信息4)在 Nacos 上配置属性5)在 Spring Boot 中使用配置6)启动服务&验证7&am…...
ElementUI安装与使用指南
Element官网-安装指南 提醒一下:下面实例讲解是在Mac系统演示的; 一、开发环境配置 电脑需要先安装好node.js和vue2或者vue3 安装Node.js Node.js 中文网 安装node.js命令:brew install node node.js安装完后,输入࿱…...
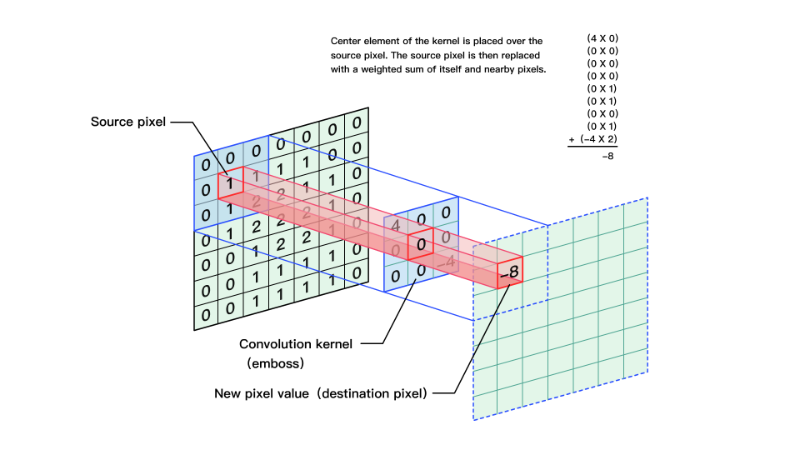
Opencv——图片卷积
图像滤波是尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,是图像预处理中不可缺少的操作,其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。 线性滤波是图像处理最基本的方法,它允许我们对图像进行处理,产生很多不同的效果。首先,我们需要一个二…...
项目安全-----加密算法实现
目录 对称加密算法 AES (ECB模式) AES(CBC 模式)。 非对称加密 对称加密算法 对称加密算法,是使用相同的密钥进行加密和解密。使用对称加密算法来加密双方的通信的话,双方需要先约定一个密钥,加密方才能加密&#…...
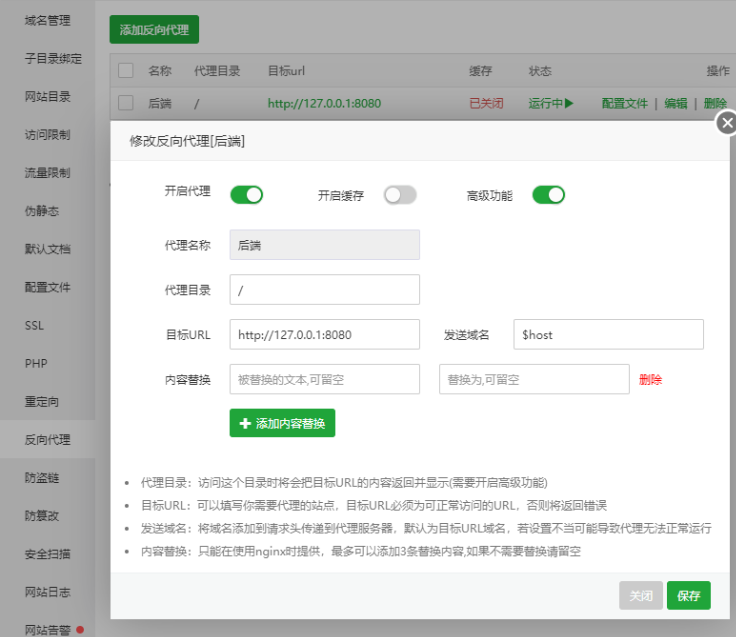
只用一台服务器部署上线(宝塔面板) 前后端+数据库
所需材料 工具:安装宝塔面板服务器至少一台、域名一个 前端:生成dist文件(前端运行build命令) 后端:生成jar包(maven运行package命令) 准备: 打开宝塔面板,点击进入软…...

《Pandas 简易速速上手小册》第8章:Pandas 高级数据分析技巧(2024 最新版)
文章目录 8.1 使用 apply 和 map 函数8.1.1 基础知识8.1.2 重点案例:客户数据清洗和转换8.1.3 拓展案例一:产品评分调整8.1.4 拓展案例二:地址格式化 8.2 性能优化技巧8.2.1 基础知识8.2.2 重点案例:大型销售数据分析8.2.3 拓展案…...

计算机网络_1.6.2 计算机网络体系结构分层的必要性
1.6.2 计算机网络体系结构分层的必要性 一、五层原理体系结构每层各自主要解决什么问题1、物理层2、数据链路层3、网络层4、运输层5、应用层 二、总结三、练习 笔记来源: B站 《深入浅出计算机网络》课程 本节主要介绍实现计算机网络需要解决哪些问题?以…...
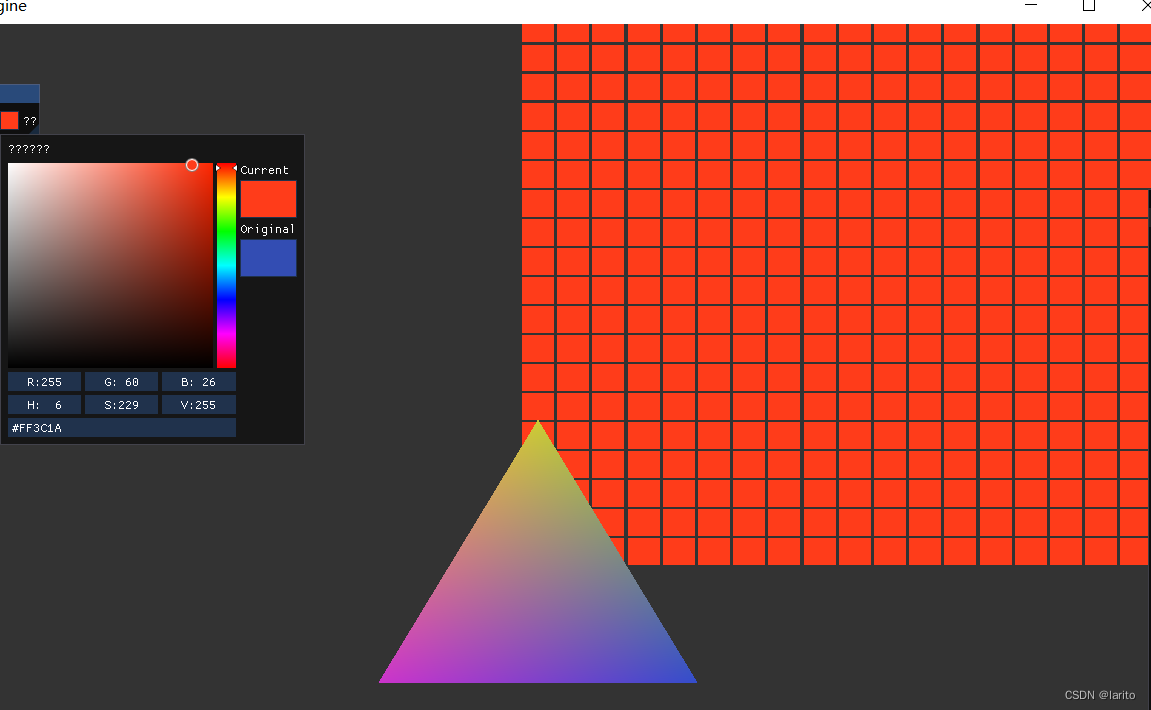
跟着cherno手搓游戏引擎【18】抽象Shader、项目小修改
抽象: Shader.h: #pragma once #include <string>namespace YOTO {class Shader {public:virtual~Shader()default;virtual void Bind()const0;virtual void UnBind()const0;static Shader* Create(const std::string& vertexSrc, const std::string&am…...

每日OJ题_算法_模拟②_力扣495. 提莫攻击
目录 力扣495. 提莫攻击 解析代码 力扣495. 提莫攻击 495. 提莫攻击 难度 简单 在《英雄联盟》的世界中,有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希(编者注:寒冰射手)进入中毒状态。 当提莫攻击艾希,…...

freertos 源码分析二 list链表源码
list.c 一、链表初始化 void vListInitialise( List_t * const pxList ) { pxList->pxIndex ( ListItem_t * ) &…...
Peter算法小课堂—Dijkstra最短路算法
大家好,我们人见人爱、花见花开、车见车爆胎的Peter Pan来啦,hia~hia~hia。今天,我们今天来学习毒瘤的最短路算法啦。啊这……什么是Dijkstra算法?长文警告⚠ 正经点啊 手算样例 大家思考一下,你在手算样例的时候&am…...

Python 读取和写入包含中文的csv、xlsx、json文件
背景 最近在做数据的训练,经常需要读取写入csv、xlsx、json文件来获取数据,在这里做简单总结记录。 ps: 读取和写入中文文件时,需要确保文件的编码格式是正确的。通常情况使用UTF-8编码格式。如果使用其他编码格式可能会导致读取或写入时出…...
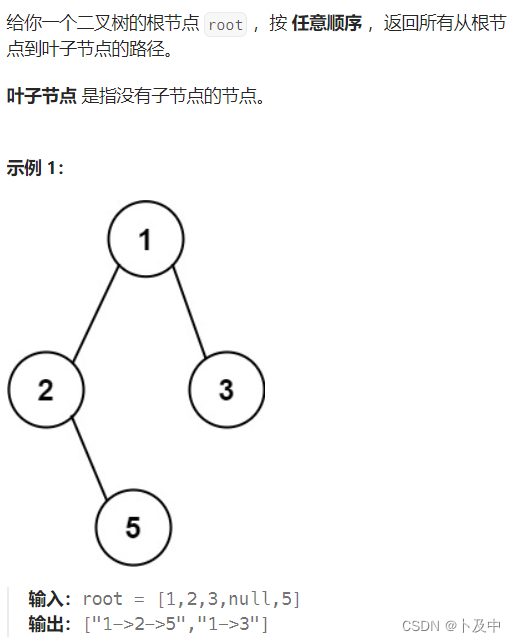
【算法】利用递归dfs解决二叉树算法题(C++)
文章目录 1. 前言2. 算法题2331.计算布尔二叉树的值129.求根节点到叶节点数字之和LCR047.二叉树剪枝98.验证二叉搜索树230.二叉搜索树中第K小的元素257.二叉树的所有路径 1. 前言 有关 递归 的相关解释与解题 请看下文: 以汉诺塔理解递归、并用递归解决算法题 对于…...

计算机网络_1.6.1 常见的三种计算机网络体系结构
1.6.1 常见的三种计算机网络体系结构 1、OSI(七层协议)标准失败的原因2、TCP/IP参考模型3、三种网络体系结构对比 笔记来源: B站 《深入浅出计算机网络》课程 1、OSI(七层协议)标准失败的原因 (1…...
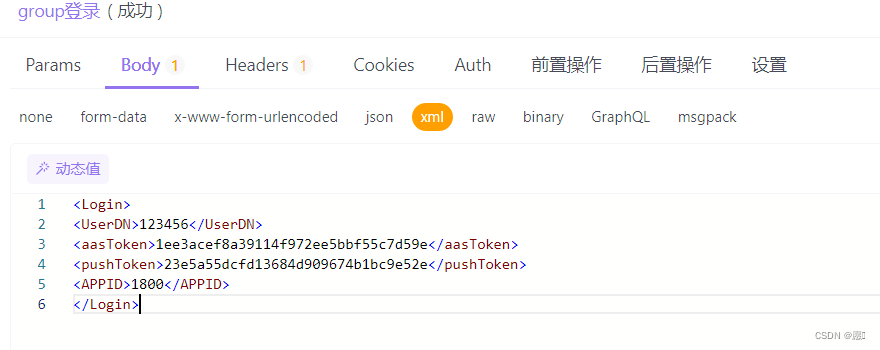
XML传参方式
export function groupLoginAPI(xmlData) {return http.post(/tis/group/1.0/login, xmlData, {headers: {Content-Type: application/xml,X-Requested-With: AAServer/4.0,}}) }import {groupLoginAPI} from "../api/user"; function (e) { //xml格式传参let groupX…...
Pyecharts炫酷散点图构建指南【第50篇—python:炫酷散点图】
文章目录 Pyecharts炫酷散点图构建指南引言安装Pyecharts基础散点图自定义散点图样式渐变散点图动态散点图高级标注散点图多系列散点图3D散点图时间轴散点图笛卡尔坐标系下的极坐标系散点图 总结: Pyecharts炫酷散点图构建指南 引言 在数据可视化领域,…...
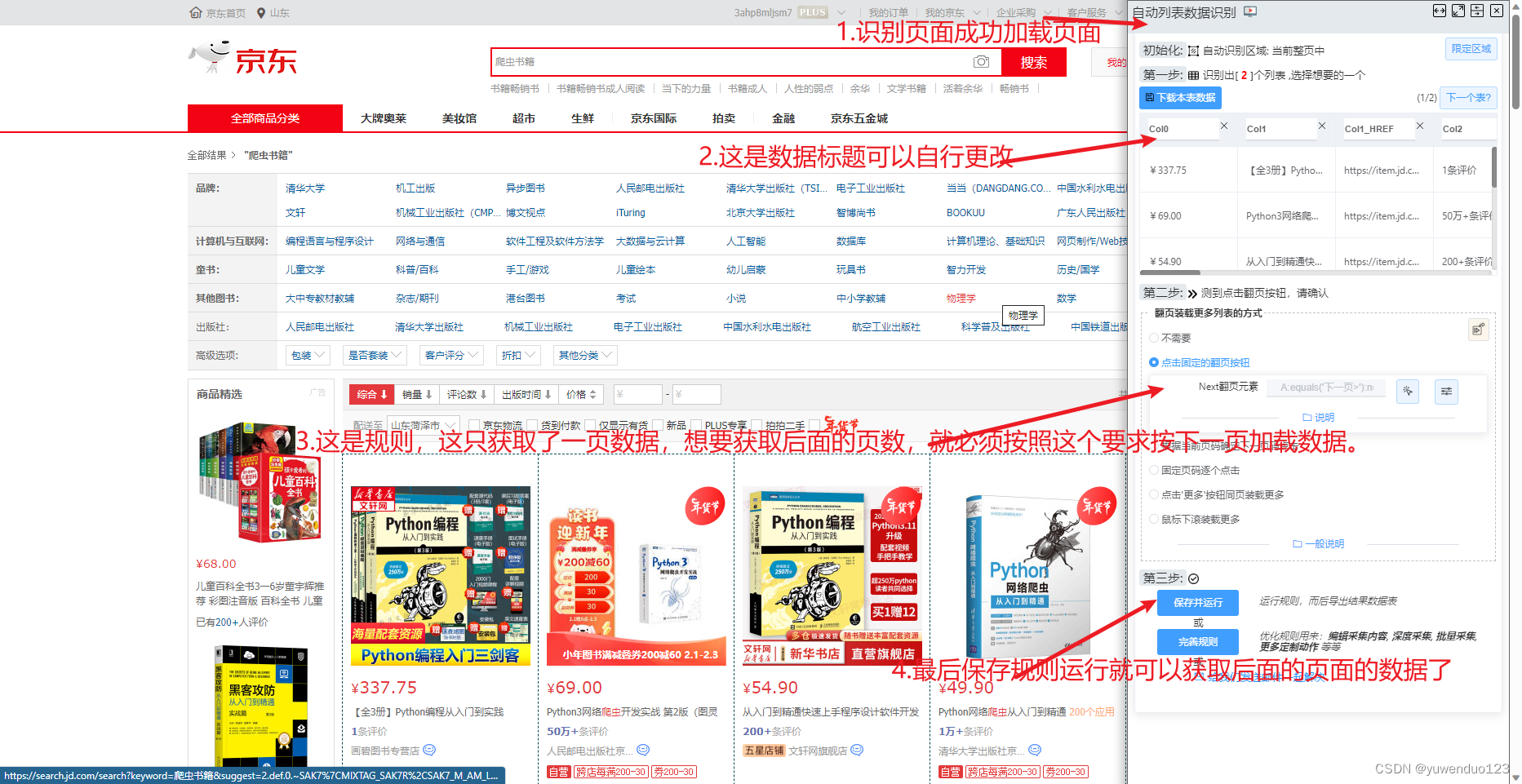
关于爬取所有哔哩哔哩、任意图片、所有音乐、的python脚本语言-Edge浏览器插件 全是干货!
这些都是现成的并且实时更新的!从次解放双手! 首先有自己的edge浏览器基本上都有并且找到插件选项 1.哔哩哔哩视频下载助手(爬取哔哩哔哩视频) bilibili哔哩哔哩视频下载助手 - Microsoft Edge Addons 下面是效果: 2.图…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
