备战蓝桥杯---数据结构与STL应用(入门4)
本专题主要是关于利用优先队列解决贪心选择上的“反悔”问题
话不多说,直接看题:
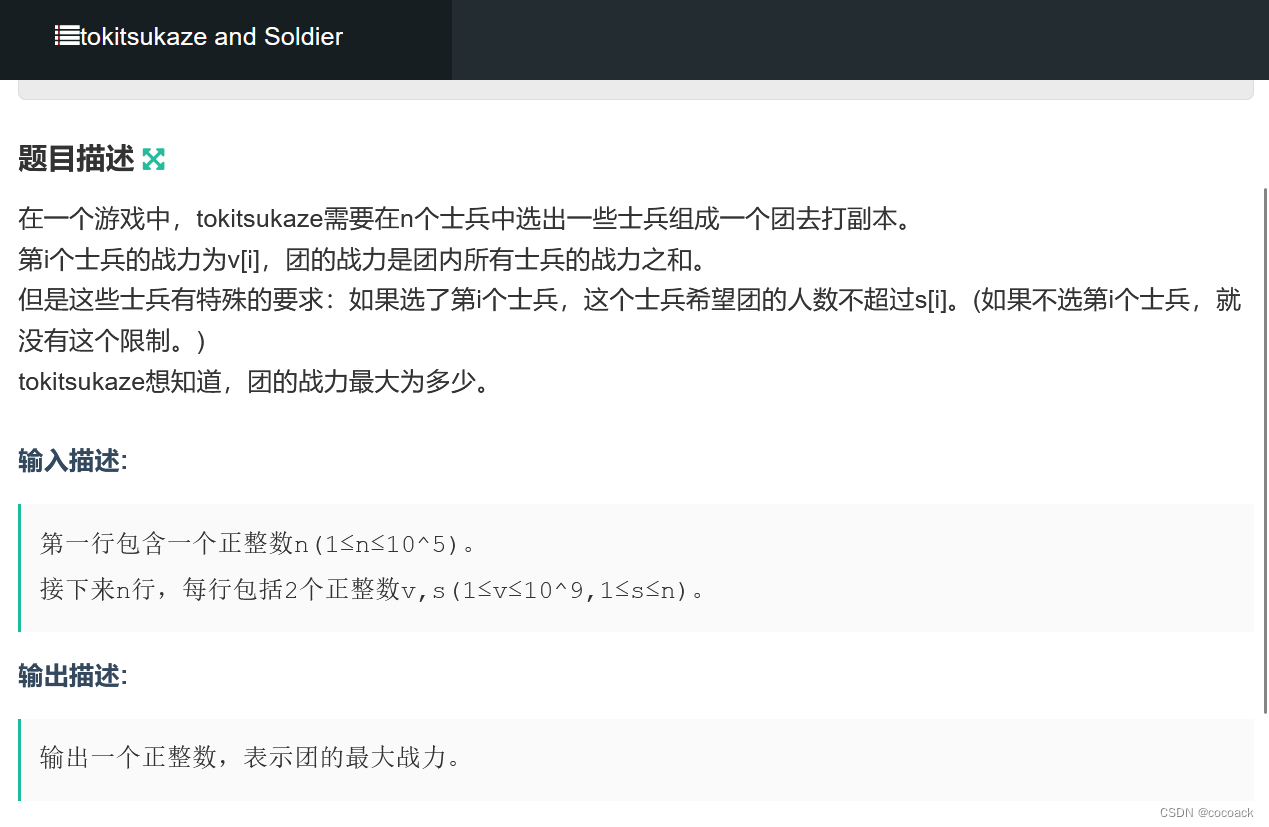
下面为分析:
很显然,我们在整体上以s[i]为基准,先把士兵按s[i]排好。然后,我们先求s[i]大的开始,即规定选人数不超过s[i]的士兵,下面为图解:

下面为AC代码:
#include<bits/stdc++.h>
using namespace std;
struct node{long long v,s;
}a[1000100];
long long n;
bool cmp(node a,node b){return a.s>b.s;
}
signed main(){cin>>n;for(int i=1;i<=n;i++){scanf("%lld%lld",&a[i].v,&a[i].s);}sort(a+1,a+1+n,cmp);priority_queue<long long,vector<long long>,greater<long long> > q;long long cap=a[1].s,sum=a[1].v,max1=-1;q.push(a[1].v);for(int i=2;i<=n;i++){if(a[i].s==cap){q.push(a[i].v);sum+=a[i].v;if(q.size()>cap){sum-=q.top();q.pop();}} else{cap=a[i].s;q.push(a[i].v);sum+=a[i].v;while(q.size()>cap){sum-=q.top();q.pop();}}max1=max(max1,sum);}cout<<max1;
}再来一道类似的:
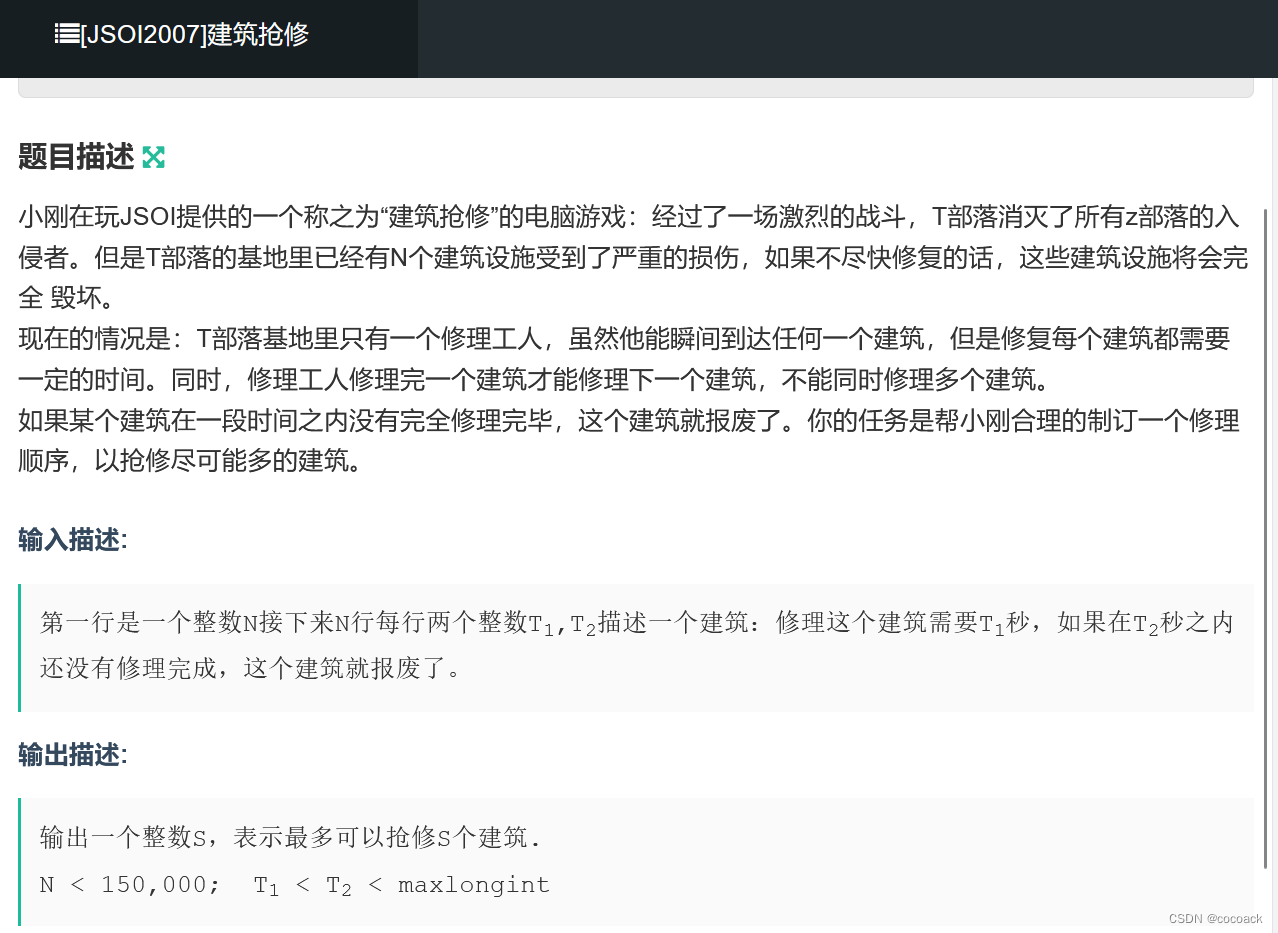
下面为分析:
类似的,我们指定一个基准,我们按deadline升序排好,从小的开始枚举。
如果前面的时间加当前所需没超当前建筑的deadline,我们就添加。
否则,我们用它与前面所需时间max的比,如果比他小就替换。
下面为AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
struct node{int t1,t2;
}a[150010];
bool cmp(node a,node b){return a.t2<b.t2;}
signed main(){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d%d",&a[i].t1,&a[i].t2);sort(a+1,a+n+1,cmp);priority_queue<int> q;int dead=-1,cnt=0,sum=0;for(int i=1;i<=n;i++){q.push(a[i].t1);cnt++;sum+=a[i].t1;if(a[i].t2!=dead) dead=a[i].t2;if(sum>dead){sum-=q.top();cnt--;q.pop();} }cout<<cnt;
}让我们总结一下,本专题围绕利用优先队列解决贪心选择上的“反悔”(或优化)问题(常用于固定枚举一个基准值)
最后,举个形象的例子:我们的成长就是从一开始的幼稚不断地经历岁月的打磨,见识的增长,不断优化,最终走向成熟。
希望可以和大家一起继续前行!
相关文章:

备战蓝桥杯---数据结构与STL应用(入门4)
本专题主要是关于利用优先队列解决贪心选择上的“反悔”问题 话不多说,直接看题: 下面为分析: 很显然,我们在整体上以s[i]为基准,先把士兵按s[i]排好。然后,我们先求s[i]大的开始,即规定选人数…...
2023_12蓝桥杯STEMA 考试 Scratch 中级试卷解析
2023蓝桥杯STEMA 考试 Scratch 中级试卷(12 月)解析 由于没有原始文件,这里使用的角色和背景和实际题目会有所差异,已经尽量还原原题,以下代码仅供参考。吐槽一句:蓝桥杯越来越变态了!\(`Δ’)/\(`Δ’)/\(`Δ’)/孩子学习速度永远也赶不上内卷的速度。 一、选择…...

从编程中理解:大脑中的杏仁核
编程和神经科学在某种程度上可以相互借鉴,尤其是在模拟大脑功能时。让我们以Unity游戏引擎中的C#代码为例,结合金庸武侠小说中的人物形象来构建一个类比故事,探讨如何通过编程模拟大脑中杏仁核的作用。 假设在一款名为“脑海江湖”的Unity游戏中,主角张无忌(代指玩家角色…...
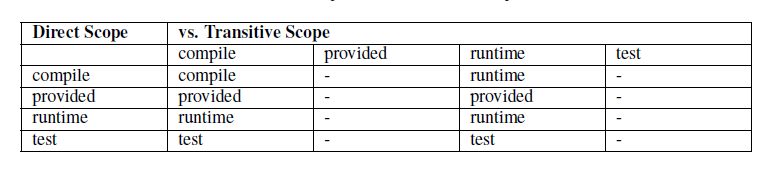
Maven dependency中的scope
Maven的一个哲学是惯例优于配置(Convention Over Configuration), Maven默认的依赖配置项中,scope的默认值是compile。 scope的分类 compile(默认) 含义: compile 是默认值,如果没有指定 scope 值,该元素…...

代码随想录算法训练营DAY11 | 栈与队列 (2)
一、LeetCode 20 有效的括号 题目链接:20.有效的括号https://leetcode.cn/problems/valid-parentheses/ 思路:遇到左括号直接进栈;遇到右括号判断站顶是否有匹配的括号,没有就返回flase,有就将栈顶元素出栈࿱…...

【Spring实战】33 Spring Boot3 集成 Nacos 配置中心
文章目录 1. 配置中心定义2. 解决哪些问题3. 常用的配置中心4. 使用示例1)没引入 Nacos 配置中心2)引入依赖3)配置Nacos连接信息4)在 Nacos 上配置属性5)在 Spring Boot 中使用配置6)启动服务&验证7&am…...
ElementUI安装与使用指南
Element官网-安装指南 提醒一下:下面实例讲解是在Mac系统演示的; 一、开发环境配置 电脑需要先安装好node.js和vue2或者vue3 安装Node.js Node.js 中文网 安装node.js命令:brew install node node.js安装完后,输入࿱…...
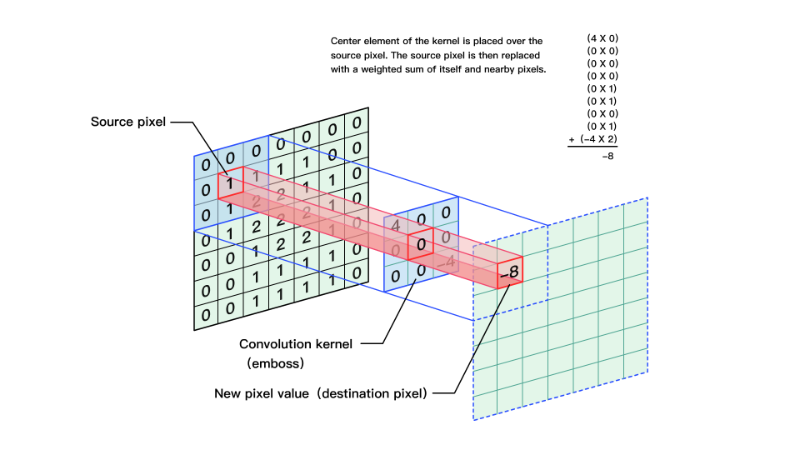
Opencv——图片卷积
图像滤波是尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,是图像预处理中不可缺少的操作,其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。 线性滤波是图像处理最基本的方法,它允许我们对图像进行处理,产生很多不同的效果。首先,我们需要一个二…...
项目安全-----加密算法实现
目录 对称加密算法 AES (ECB模式) AES(CBC 模式)。 非对称加密 对称加密算法 对称加密算法,是使用相同的密钥进行加密和解密。使用对称加密算法来加密双方的通信的话,双方需要先约定一个密钥,加密方才能加密&#…...
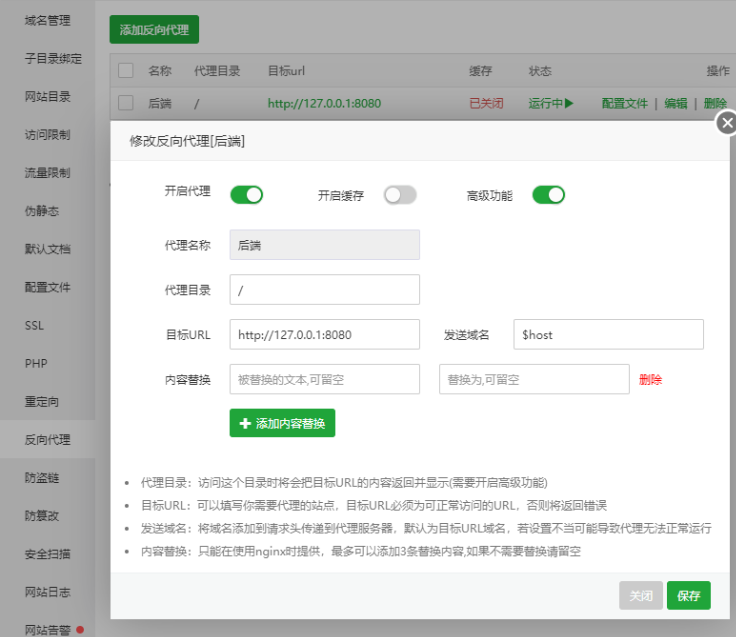
只用一台服务器部署上线(宝塔面板) 前后端+数据库
所需材料 工具:安装宝塔面板服务器至少一台、域名一个 前端:生成dist文件(前端运行build命令) 后端:生成jar包(maven运行package命令) 准备: 打开宝塔面板,点击进入软…...

《Pandas 简易速速上手小册》第8章:Pandas 高级数据分析技巧(2024 最新版)
文章目录 8.1 使用 apply 和 map 函数8.1.1 基础知识8.1.2 重点案例:客户数据清洗和转换8.1.3 拓展案例一:产品评分调整8.1.4 拓展案例二:地址格式化 8.2 性能优化技巧8.2.1 基础知识8.2.2 重点案例:大型销售数据分析8.2.3 拓展案…...

计算机网络_1.6.2 计算机网络体系结构分层的必要性
1.6.2 计算机网络体系结构分层的必要性 一、五层原理体系结构每层各自主要解决什么问题1、物理层2、数据链路层3、网络层4、运输层5、应用层 二、总结三、练习 笔记来源: B站 《深入浅出计算机网络》课程 本节主要介绍实现计算机网络需要解决哪些问题?以…...
跟着cherno手搓游戏引擎【18】抽象Shader、项目小修改
抽象: Shader.h: #pragma once #include <string>namespace YOTO {class Shader {public:virtual~Shader()default;virtual void Bind()const0;virtual void UnBind()const0;static Shader* Create(const std::string& vertexSrc, const std::string&am…...

每日OJ题_算法_模拟②_力扣495. 提莫攻击
目录 力扣495. 提莫攻击 解析代码 力扣495. 提莫攻击 495. 提莫攻击 难度 简单 在《英雄联盟》的世界中,有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希(编者注:寒冰射手)进入中毒状态。 当提莫攻击艾希,…...

freertos 源码分析二 list链表源码
list.c 一、链表初始化 void vListInitialise( List_t * const pxList ) { pxList->pxIndex ( ListItem_t * ) &…...
Peter算法小课堂—Dijkstra最短路算法
大家好,我们人见人爱、花见花开、车见车爆胎的Peter Pan来啦,hia~hia~hia。今天,我们今天来学习毒瘤的最短路算法啦。啊这……什么是Dijkstra算法?长文警告⚠ 正经点啊 手算样例 大家思考一下,你在手算样例的时候&am…...

Python 读取和写入包含中文的csv、xlsx、json文件
背景 最近在做数据的训练,经常需要读取写入csv、xlsx、json文件来获取数据,在这里做简单总结记录。 ps: 读取和写入中文文件时,需要确保文件的编码格式是正确的。通常情况使用UTF-8编码格式。如果使用其他编码格式可能会导致读取或写入时出…...
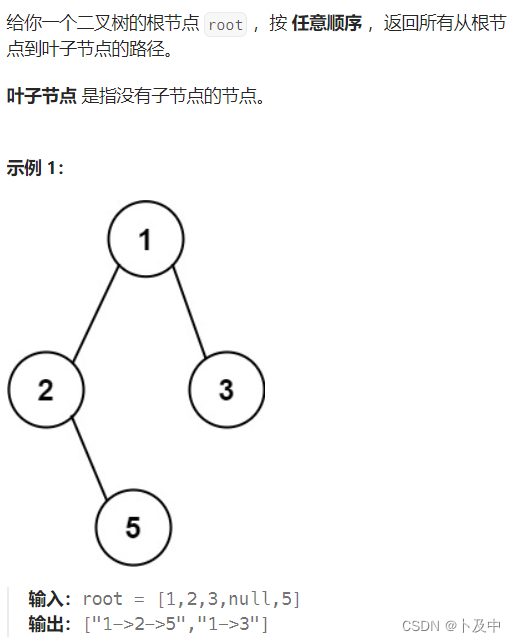
【算法】利用递归dfs解决二叉树算法题(C++)
文章目录 1. 前言2. 算法题2331.计算布尔二叉树的值129.求根节点到叶节点数字之和LCR047.二叉树剪枝98.验证二叉搜索树230.二叉搜索树中第K小的元素257.二叉树的所有路径 1. 前言 有关 递归 的相关解释与解题 请看下文: 以汉诺塔理解递归、并用递归解决算法题 对于…...

计算机网络_1.6.1 常见的三种计算机网络体系结构
1.6.1 常见的三种计算机网络体系结构 1、OSI(七层协议)标准失败的原因2、TCP/IP参考模型3、三种网络体系结构对比 笔记来源: B站 《深入浅出计算机网络》课程 1、OSI(七层协议)标准失败的原因 (1…...
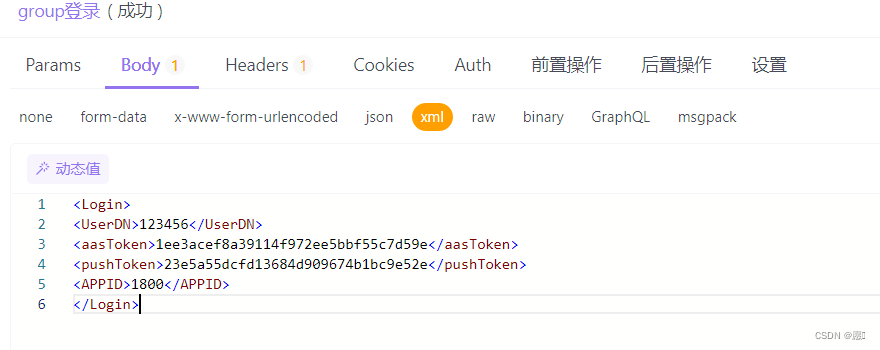
XML传参方式
export function groupLoginAPI(xmlData) {return http.post(/tis/group/1.0/login, xmlData, {headers: {Content-Type: application/xml,X-Requested-With: AAServer/4.0,}}) }import {groupLoginAPI} from "../api/user"; function (e) { //xml格式传参let groupX…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
