2024美赛C题完整解题教程及代码 网球运动的势头
2024 MCM
Problem C: Momentum in Tennis (网球运动的势头)
注:在网球运动中,"势头"通常指的是比赛中因一系列事件(如连续得分)而形成的动力或趋势,这可能对比赛结果产生重要影响。球员或团队在获得势头后,通常会表现出更高的士气和信心,可能更容易连续赢得后续的分数或局数。然而,势头的存在和其对比赛结果的实际影响很难量化,因为它涉及到许多主观和心理因素。
C题属于运动数据分析和预测的数学建模题目。它要求建立模型来分析和预测网球比赛中的势头变化,评估特定因素如何影响比赛结果。解决这类问题的思路通常包括:
- 数据收集与预处理:整理比赛中每个得分的数据,包括发球方、得分情况等。
- 势头定义与量化:确定如何量化势头,可能包括连续得分、破发等指标。
- 统计分析:使用统计方法分析势头与比赛结果之间的关系。
- 模型建立:基于历史数据,使用机器学习或其他统计模型来预测比赛中的势头变化。
- 验证与调整:使用新的比赛数据测试模型的准确性,并根据结果调整模型。
这要求对数据进行深入分析,以及运用统计学和机器学习知识来构建和验证模型。
完整思路视频大家可以看下B站:
2024美赛C题网球运动的势头思路(附代码+全保姆教程)_哔哩哔哩_bilibili
题目:
在2023年温布尔顿网球公开赛男子单打决赛中,20岁的西班牙新星卡洛斯·阿尔卡拉斯击败了36岁的诺瓦克·德约科维奇。这是德约科维奇自2013年以来在温布尔顿的首次失利,结束了这位网球史上最伟大球员之一在大满贯赛事中的非凡成就。比赛本身是一场激烈的战斗。德约科维奇在第一盘以6-1轻松占据上风,但第二盘却紧张不已,最终阿尔卡拉斯以7-6(抢七胜)赢得胜利。第三盘阿尔卡拉斯以6-1轻松取胜,第四盘虽然一开始阿尔卡拉斯似乎完全掌控比赛,但德约科维奇又完全控制了局面,以6-3赢得该盘。最终阿尔卡拉斯在第五盘以6-4获胜。这场比赛的数据包含在提供的数据集中,使用“match_id”为“2023-wimbledon-1701”来查看。这场比赛的惊人转折,有时是许多分数甚至是局数的变化,通常被归因于“势头”。势头在体育中被定义为一连串事件或运动获得的力量或强度,但很难衡量这种现象,也不容易明确比赛中的各种事件如何创造或改变势头
问题一:开发一个模型,捕捉比赛中分数变化的流程,并将其应用于一场或多场比赛。模型应能识别在比赛特定时刻哪位球员表现更佳及表现的优势程度。提供一种基于模型的可视化方法来展示比赛流程。值得注意的是,在网球比赛中,发球方赢得分数/局的概率较高,这一点可以在模型中得到体现。



问题二:网球教练对“势头”在比赛中的作用表示怀疑,认为比赛中的转折和某一球员的连胜是随机的。使用你的模型/指标来评估这一说法。




问题三:教练希望了解是否存在指标,能帮助预测比赛流程何时会从偏向一位球员转变为偏向另一位。利用至少一场比赛的数据,开发一个模型来预测比赛中的这些转折。哪些因素似乎最相关?





问题四:考虑到过去比赛中“势头”的变化,你如何建议球员准备与不同对手的新比赛?在一场或多场其他比赛上测试你开发的模型。模型预测比赛中转折的准确性如何?如果模型某些时候表现不佳,你能识别出未来模型中可能需要包含的任何因素吗?你的模型对其他比赛(如女子比赛)、不同类型的锦标赛、不同的场地表面以及其他运动(如乒乓球)有多大的普适性?





问题五::撰写不超过25页的报告,总结你的发现,并包括一到两页的备忘录,为教练总结你的结果,提供关于“势头”的作用以及如何准备球员应对影响比赛流程的事件的建议。
Examples to Help Understand the Data Set
为了帮助理解数据集,这部分提供了一些例子。这些例子可能包括如何解读数据集中的特定条目,比如比赛的得分过程、球员间的对比、比赛中的关键时刻等。通过具体的数据点,这些例子旨在展示如何使用数据集来分析比赛流程、球员表现和比赛结果等方面。




相关文章:

2024美赛C题完整解题教程及代码 网球运动的势头
2024 MCM Problem C: Momentum in Tennis (网球运动的势头) 注:在网球运动中,"势头"通常指的是比赛中因一系列事件(如连续得分)而形成的动力或趋势,这可能对比赛结果产生重要影响。球…...
二、人工智能之提示工程(Prompt Engineering)
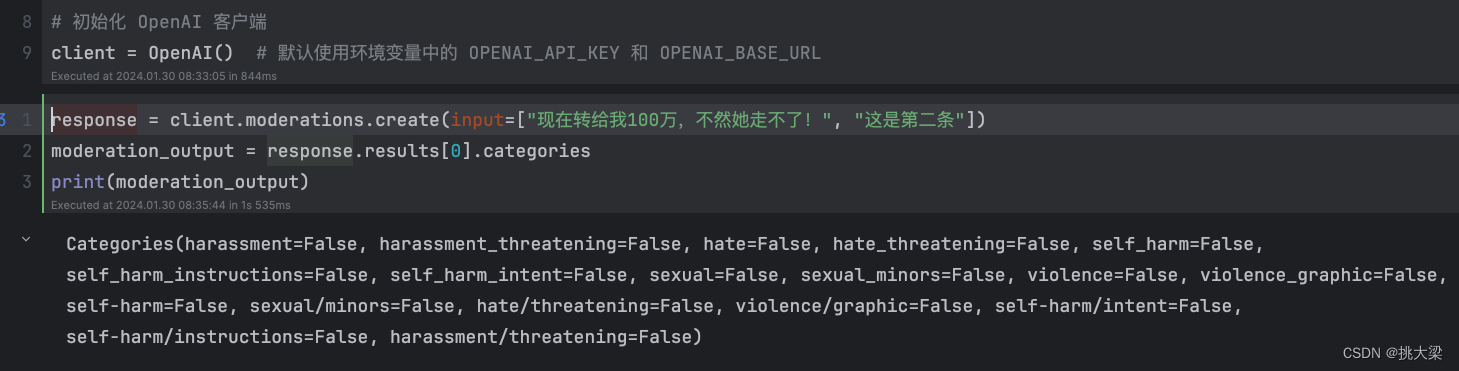
黑8说 岁月如流水匆匆过,哭一哭笑一笑不用说。 黑8自那次和主任谈话后,对这个“妖怪”继续研究,开始学习OpenAI API!关注到了提示工程(Prompt Engineering)的重要性,它包括明确的角色定义、自然语言理解(…...
【leetcode题解C++】98.验证二叉搜索树 and 701.二叉搜索树中的插入操作
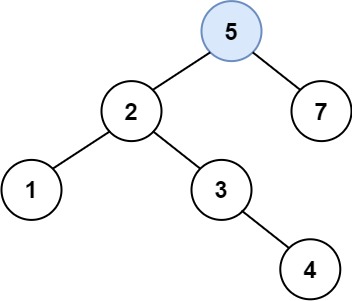
98. 验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 示例…...

【Vue.js设计与实现】第二篇:响应系统-阅读笔记(持续更新)
从高层设计的角度去探讨框架需要关注的问题。 系列目录: 标题博客第一篇:框架设计概览【Vue.js设计与实现】第一篇:框架设计概览-阅读笔记第二篇:响应系统【Vue.js设计与实现】第二篇:响应系统-阅读笔记第三篇&#x…...
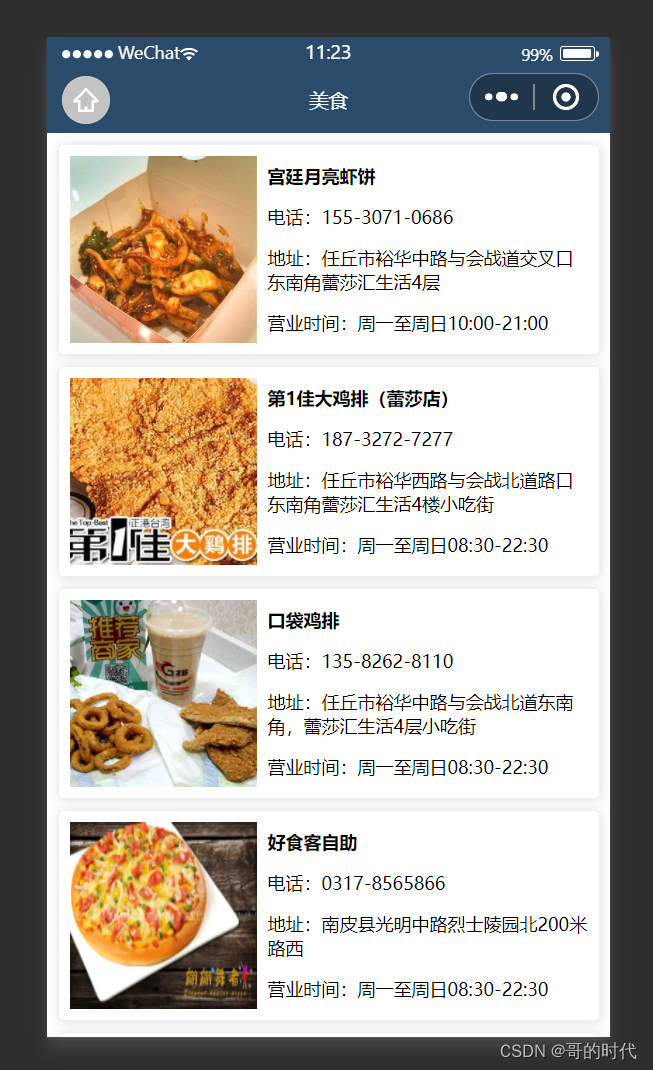
微信小程序之本地生活案例的实现
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

智能决策的艺术:探索商业分析的最佳工具和方法
文章目录 一、引言二、商业分析思维概述三、数据分析在商业实践中的应用四、如何培养商业分析思维与实践能力五、结论《商业分析思维与实践:用数据分析解决商业问题》亮点内容简介作者简介目录获取方式 一、引言 随着大数据时代的来临,商业分析思维与实…...
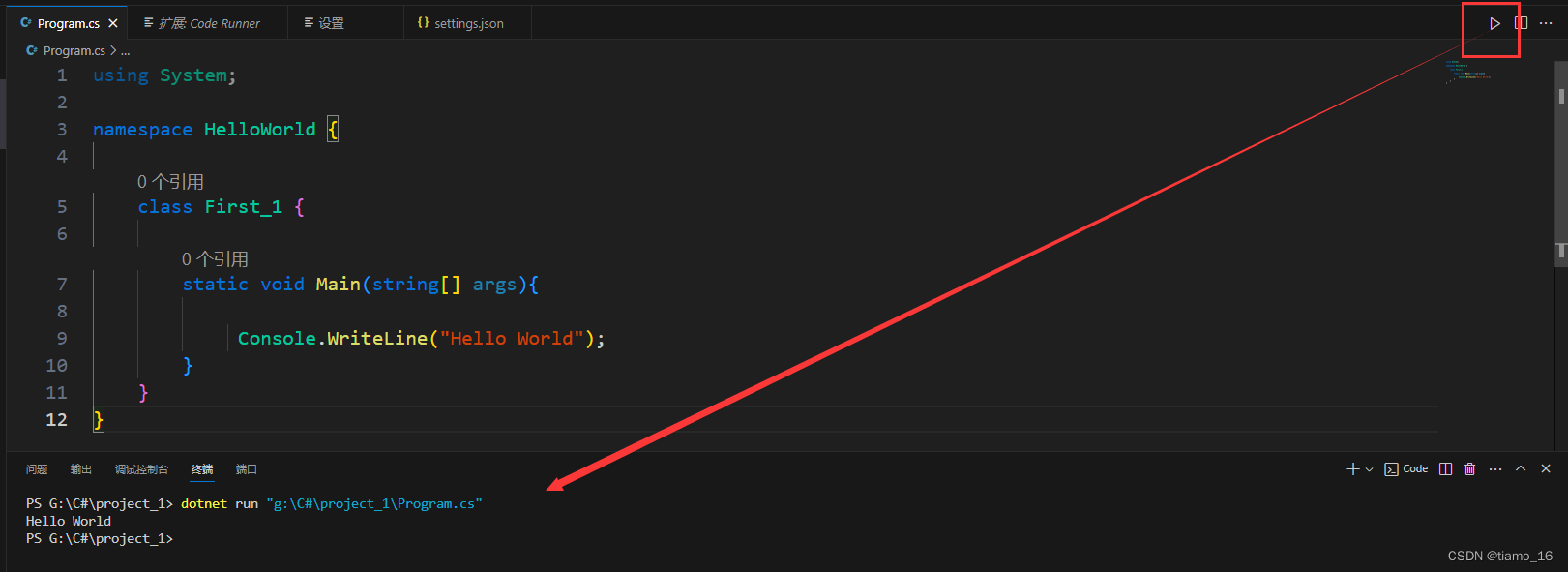
C#(C Sharp)学习笔记_前言及Visual Studio Code配置C#运行环境【一】
前言 这可以说是我第一次正式的踏入C#的学习道路,我真没想过我两年前是怎么跳过C#去学Unity3D游戏开发的(当然了,游戏开发肯定是没有成功的,都是照搬代码)。而现在,我真正地学习一下C#,就和去年…...
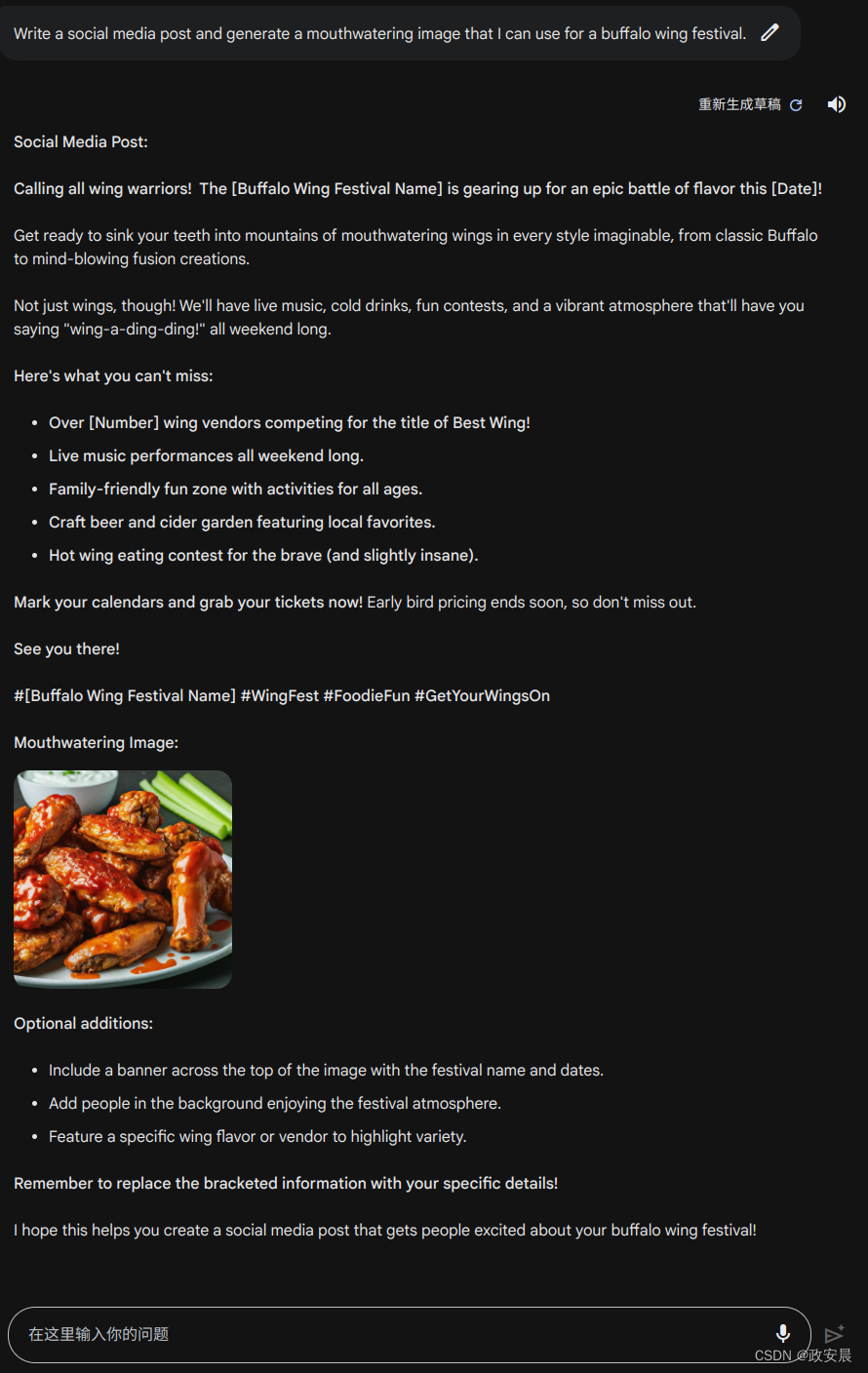
政安晨的AI笔记——Bard大模型最新提示词创作绘画分析
AI大模型进入商业应用元年后的第一年,顶级模型大混战终于开始了。 Bard在追赶OpenAI的过程中,还是补上了画图的短板。 (相比于视频的5阶张量处理而言,图画做为4阶张量处理虽然不新鲜,但却是跨不过去的基础条件&#…...

基础算法bfs -剪枝问题
问题描述:一个迷宫有 NXM 格,有一些格子是地板,能走;有一些格子是障碍,不能走。给一个起点S和一个终点D。一只小狗从 S出发,每步走一块地板,在每块地员不能停留,而且走过的地板都不能再走。给定一个 T,问小狗能正好走 T步到达D吗?输入:有很多测试样例。…...

在Meteor Lake上测试基于Stable Diffusion的AI应用
上个月刚刚推出的英特尔新一代Meteor Lake CPU,预示着AI PC的新时代到来。AI PC可以不依赖服务器直接在PC端处理AI推理工作负载,例如生成图像或转录音频。这些芯片的正式名称为Intel Core Ultra处理器,是首款配备专门用于处理人工智能任务的 …...

情人节心动礼物:共度情人节美好时刻的礼物推荐
情人节,这个充满浪漫与爱意的特殊日子,总是让人心跳加速,期待着与爱人共享甜蜜时光。在这一天,送出一份精心挑选的礼物,不仅能够表达你对另一半无尽的爱意,更能让这份爱升华,成为你们爱情故事中…...
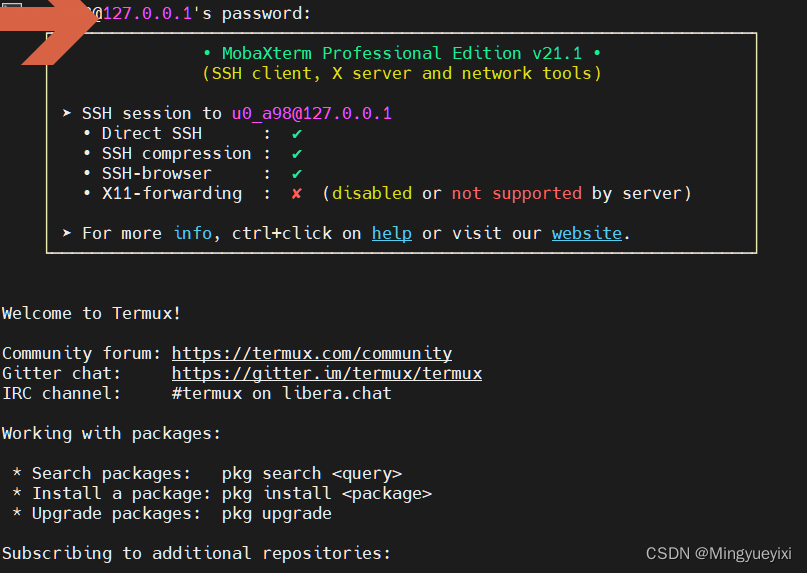
远程手机搭建Termux环境,并通过ssh连接Termux
背景 Termux只能通过鼠标点击,无法使用电脑键盘,输入速度很慢,你想通过ssh 连接Termux,获得友好体验搞了个云手机,想像普通手机那样充当服务器想把自己的手机公开到局域网中供同事调试想把自己的模拟器公开到局域网中…...

基于EdgeWorkers的边缘应用如何进行单元测试?
随着各行各业数字化转型的持续深入,越来越多企业开始选择将一些应用程序放在距离最终用户更近的边缘位置来运行,借此降低延迟,提高应用程序响应速度,打造更出色的用户体验。 相比传统集中部署和运行的方式,这种边缘应…...

【linux】校招中的“熟悉linux操作系统”一般是指达到什么程度?
这样,你先在网上找一套完整openssh升级方案(不是yum或apt的,要源码安装的),然后在虚拟机上反复安装测试,直到把他理解了、背下来。 面试的时候让你简单说说linux命令什么的,你就直接把这个方案…...

【CSS系列】常用容易忽略的css
user-select user-select 是一个 CSS 属性,用于控制用户是否可以选择文本。通过设置 user-select 的值,可以决定用户是否可以选择元素中的文本,以及如何选择文本。 auto:默认值。浏览器可以选择文本。none:用户不能选…...
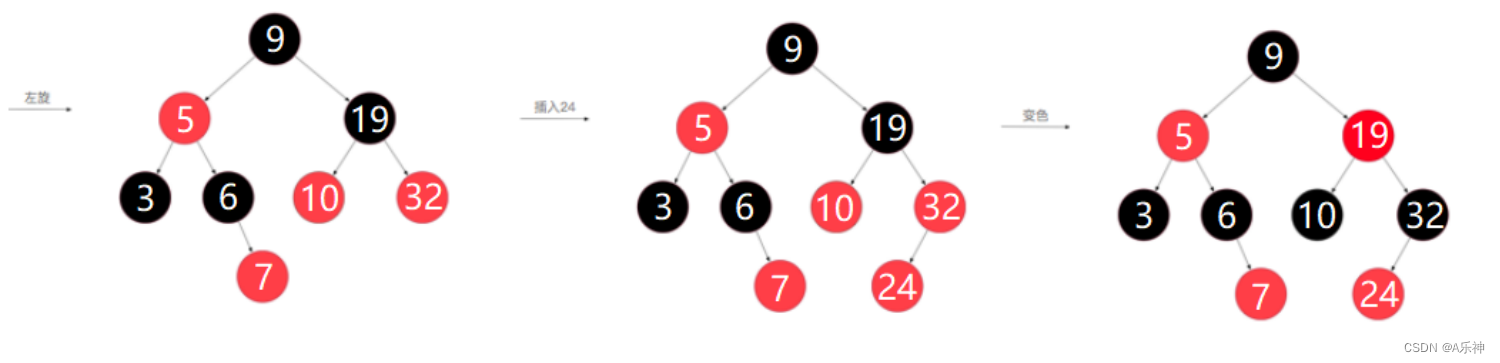
Java 数据结构 二叉树(二)红黑树
目录 数据结构图-树 简介 规则 旋转 重新着色 红黑树构建过程 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步…...

React18-完成弹窗封装
弹框封装 用法 // 创建 userRef.current?.open(create) // 修改 userRef.current?.open(edit,values){/* 创建用户 */} <CreateUser mRef{userRef} update{} />组件暴露open方法 文档地址:https://react.dev/reference/react/useImperativeHandle useIm…...

蓝桥杯2024/1/31-----底层测试模板
和之前一样建好工程文件夹,里边包含User(放工程文件,mian.c)、Driver(存放底层文件如Led.c,Led.h等) 新建的工程先搭建框架,可以先书写底层函数(此次书写了四个函数并包含…...
-高精度-乘-低精度)
蓝桥杯备战(AcWing算法基础课)-高精度-乘-低精度
目录 前言 1 题目描述 2 分析 2.1 关键代码 2.2 关键代码分析 3 代码 前言 详细的代码里面有自己的理解注释 1 题目描述 给定两个非负整数(不含前导 00) A 和 B,请你计算 AB 的值。 输入格式 共两行,第一行包含整数 A&a…...

C++设计模式-里氏替换原则
里氏替换原则定义了继承规范。(封装、继承、多态) 定义1:类型S对象o1,类型T对象o2,o1换成o2时程序意图不变,那么S是T的子类。 定义2:使用子类不破坏父类的意图。 注意:如果子类不…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
