【leetcode题解C++】98.验证二叉搜索树 and 701.二叉搜索树中的插入操作
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
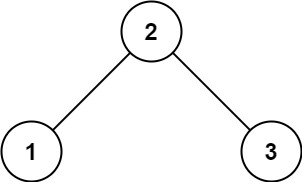
输入:root = [2,1,3] 输出:true
示例 2:
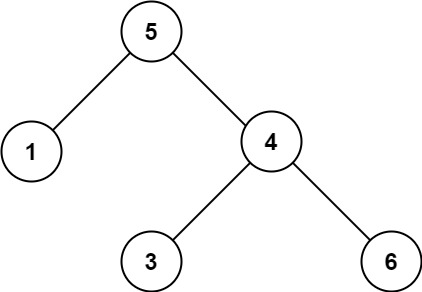
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
思路:要验证肯定要遍历,想到如果符合二叉搜索树的话,中序遍历的结果就会是从小到大的,判断一下即可。若需要判断,那么需要加上一个临时结点来记录上一个遍历的结点。
代码实现:
class Solution {
public:bool isValidBST(TreeNode* root) {stack<TreeNode *> stk;TreeNode *cur = root;TreeNode *pre = nullptr;while(cur || !stk.empty()) {if(cur) {stk.push(cur);cur = cur->left;}else {cur = stk.top();stk.pop();if(pre && cur->val <= pre->val) return false;pre = cur;cur = cur->right;}}return true;}
};701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
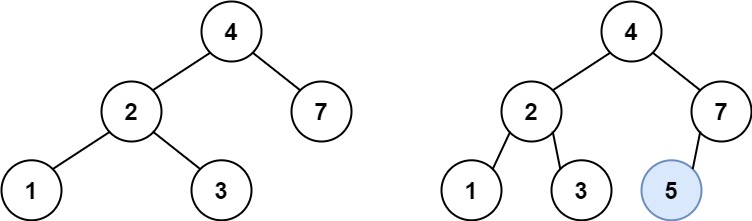
输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:
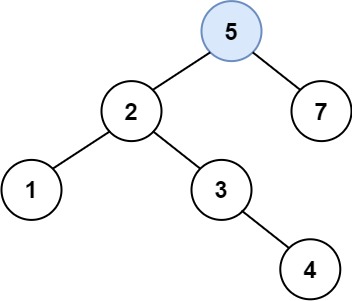
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
思路:想了想,要是重构二叉树好像有些复杂,这样的话,始终添加为叶子结点就好。那么,还是会用到两个结点,一个cur用于遍历和判断,另一个pre用于在判断找到叶子结点后,再判断添加为左孩子(新节点小)还是右孩子(新节点大)。
代码实现:
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root == nullptr) {TreeNode *node = new TreeNode(val);return node;}TreeNode *cur = root;TreeNode *pre = nullptr;while(cur) {pre = cur;if(cur->val > val) cur = cur->left;else if(cur->val <= val) cur = cur->right;}TreeNode *node = new TreeNode(val);if(pre->val > val) pre->left = node;else if(pre->val <= val) pre->right = node;return root;}
};相关文章:

【leetcode题解C++】98.验证二叉搜索树 and 701.二叉搜索树中的插入操作
98. 验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 示例…...

【Vue.js设计与实现】第二篇:响应系统-阅读笔记(持续更新)
从高层设计的角度去探讨框架需要关注的问题。 系列目录: 标题博客第一篇:框架设计概览【Vue.js设计与实现】第一篇:框架设计概览-阅读笔记第二篇:响应系统【Vue.js设计与实现】第二篇:响应系统-阅读笔记第三篇&#x…...
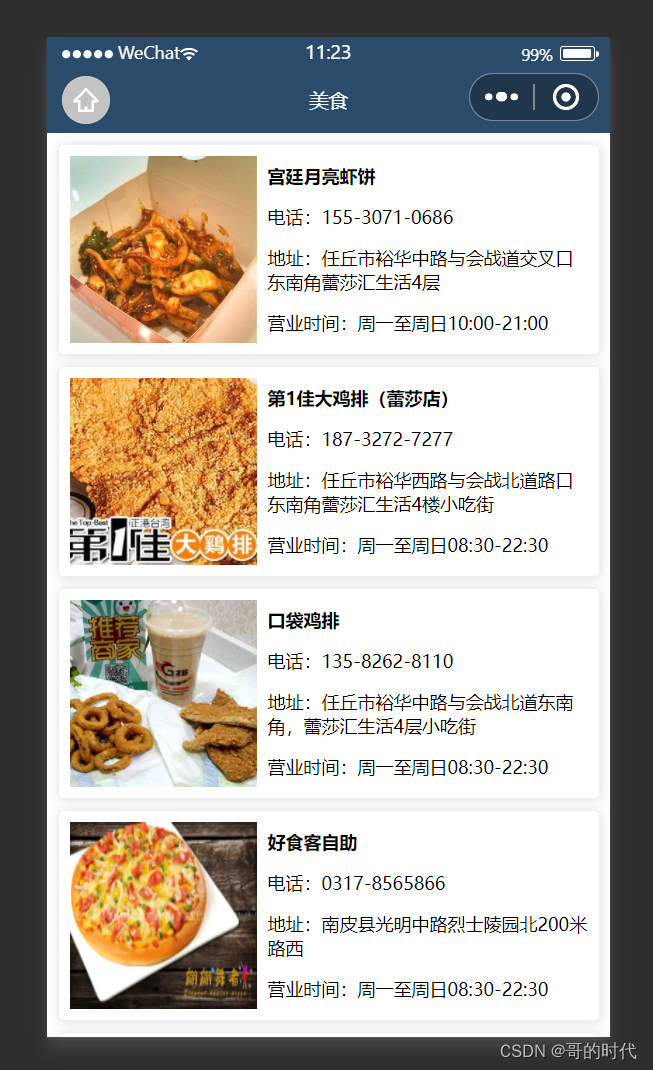
微信小程序之本地生活案例的实现
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

智能决策的艺术:探索商业分析的最佳工具和方法
文章目录 一、引言二、商业分析思维概述三、数据分析在商业实践中的应用四、如何培养商业分析思维与实践能力五、结论《商业分析思维与实践:用数据分析解决商业问题》亮点内容简介作者简介目录获取方式 一、引言 随着大数据时代的来临,商业分析思维与实…...
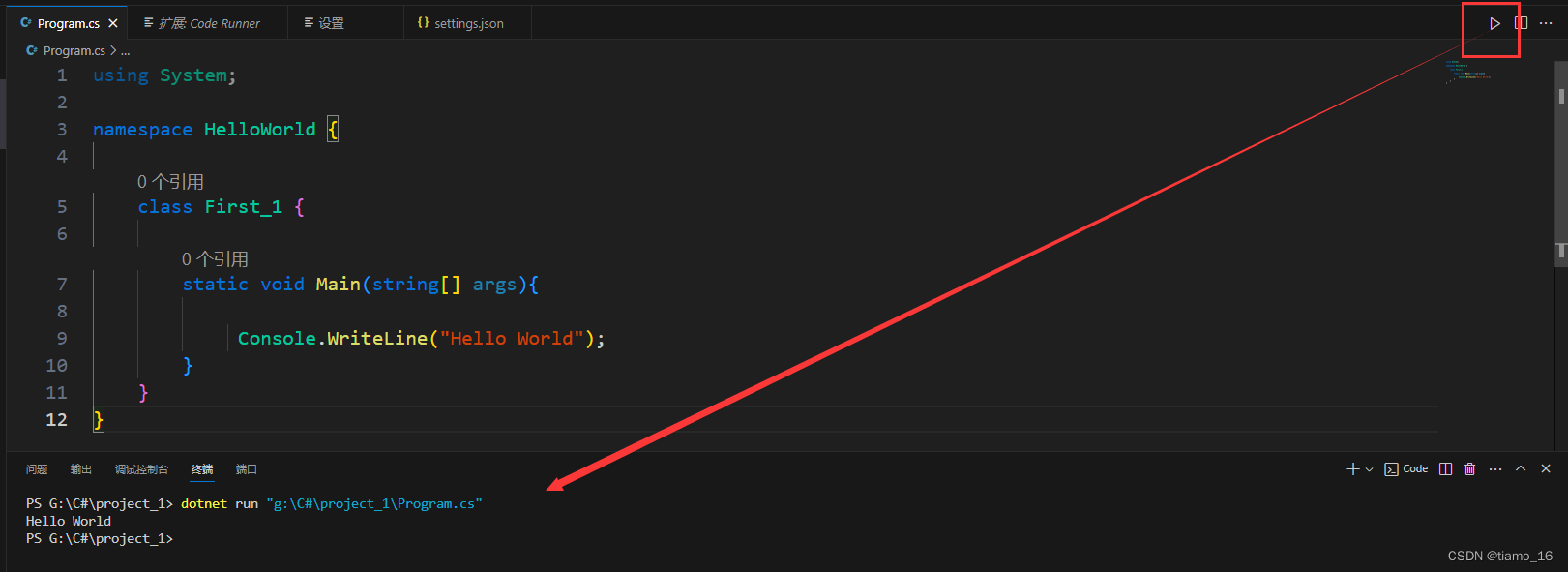
C#(C Sharp)学习笔记_前言及Visual Studio Code配置C#运行环境【一】
前言 这可以说是我第一次正式的踏入C#的学习道路,我真没想过我两年前是怎么跳过C#去学Unity3D游戏开发的(当然了,游戏开发肯定是没有成功的,都是照搬代码)。而现在,我真正地学习一下C#,就和去年…...
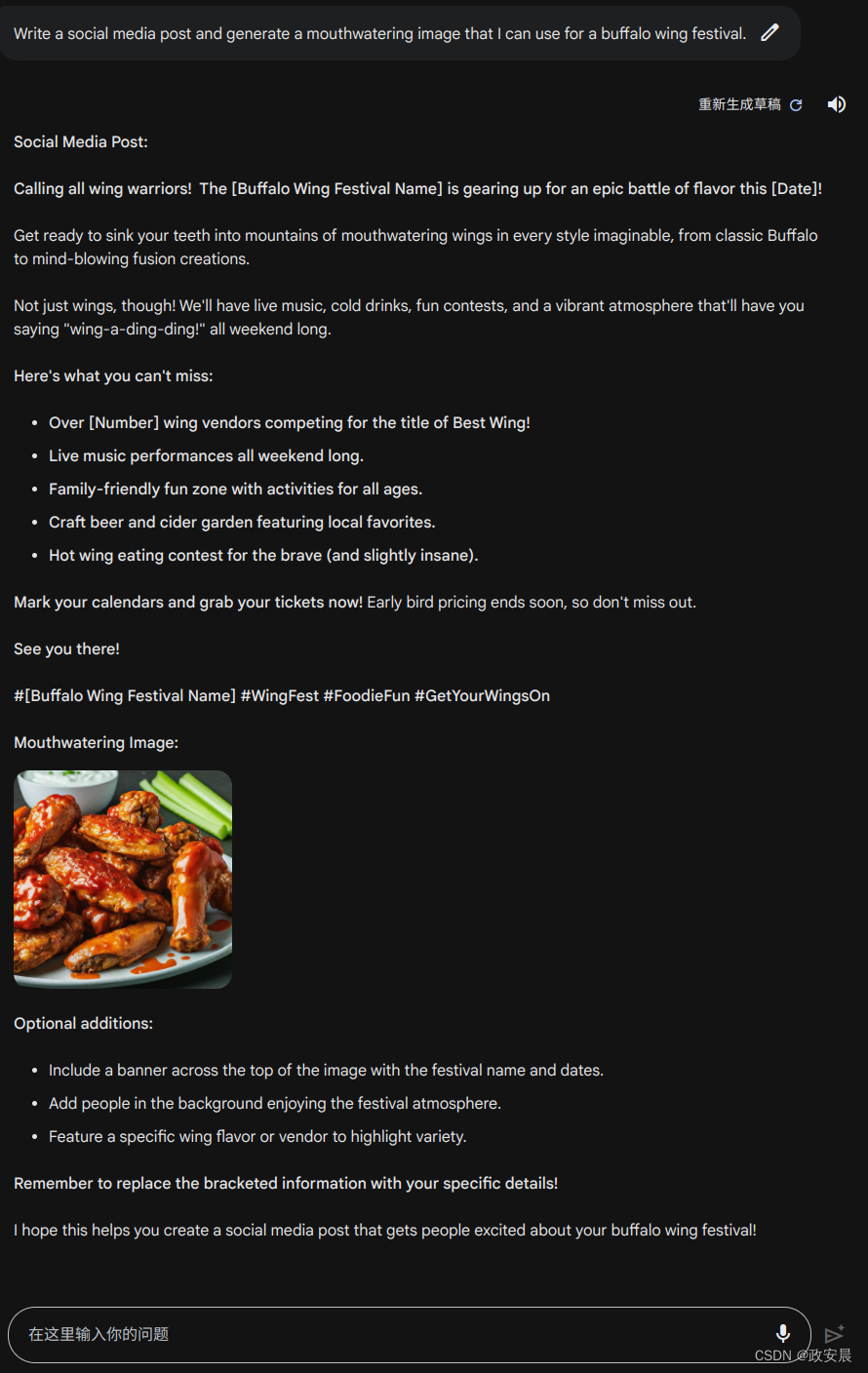
政安晨的AI笔记——Bard大模型最新提示词创作绘画分析
AI大模型进入商业应用元年后的第一年,顶级模型大混战终于开始了。 Bard在追赶OpenAI的过程中,还是补上了画图的短板。 (相比于视频的5阶张量处理而言,图画做为4阶张量处理虽然不新鲜,但却是跨不过去的基础条件&#…...

基础算法bfs -剪枝问题
问题描述:一个迷宫有 NXM 格,有一些格子是地板,能走;有一些格子是障碍,不能走。给一个起点S和一个终点D。一只小狗从 S出发,每步走一块地板,在每块地员不能停留,而且走过的地板都不能再走。给定一个 T,问小狗能正好走 T步到达D吗?输入:有很多测试样例。…...

在Meteor Lake上测试基于Stable Diffusion的AI应用
上个月刚刚推出的英特尔新一代Meteor Lake CPU,预示着AI PC的新时代到来。AI PC可以不依赖服务器直接在PC端处理AI推理工作负载,例如生成图像或转录音频。这些芯片的正式名称为Intel Core Ultra处理器,是首款配备专门用于处理人工智能任务的 …...

情人节心动礼物:共度情人节美好时刻的礼物推荐
情人节,这个充满浪漫与爱意的特殊日子,总是让人心跳加速,期待着与爱人共享甜蜜时光。在这一天,送出一份精心挑选的礼物,不仅能够表达你对另一半无尽的爱意,更能让这份爱升华,成为你们爱情故事中…...
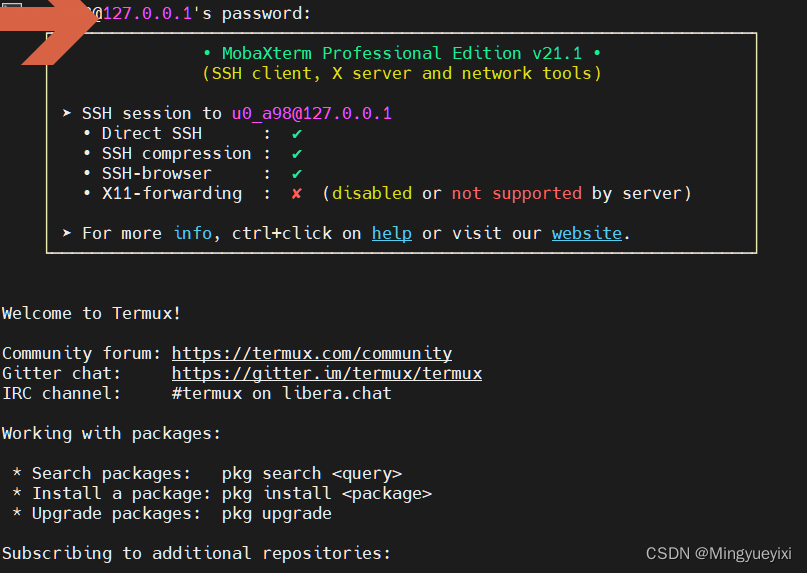
远程手机搭建Termux环境,并通过ssh连接Termux
背景 Termux只能通过鼠标点击,无法使用电脑键盘,输入速度很慢,你想通过ssh 连接Termux,获得友好体验搞了个云手机,想像普通手机那样充当服务器想把自己的手机公开到局域网中供同事调试想把自己的模拟器公开到局域网中…...

基于EdgeWorkers的边缘应用如何进行单元测试?
随着各行各业数字化转型的持续深入,越来越多企业开始选择将一些应用程序放在距离最终用户更近的边缘位置来运行,借此降低延迟,提高应用程序响应速度,打造更出色的用户体验。 相比传统集中部署和运行的方式,这种边缘应…...

【linux】校招中的“熟悉linux操作系统”一般是指达到什么程度?
这样,你先在网上找一套完整openssh升级方案(不是yum或apt的,要源码安装的),然后在虚拟机上反复安装测试,直到把他理解了、背下来。 面试的时候让你简单说说linux命令什么的,你就直接把这个方案…...

【CSS系列】常用容易忽略的css
user-select user-select 是一个 CSS 属性,用于控制用户是否可以选择文本。通过设置 user-select 的值,可以决定用户是否可以选择元素中的文本,以及如何选择文本。 auto:默认值。浏览器可以选择文本。none:用户不能选…...
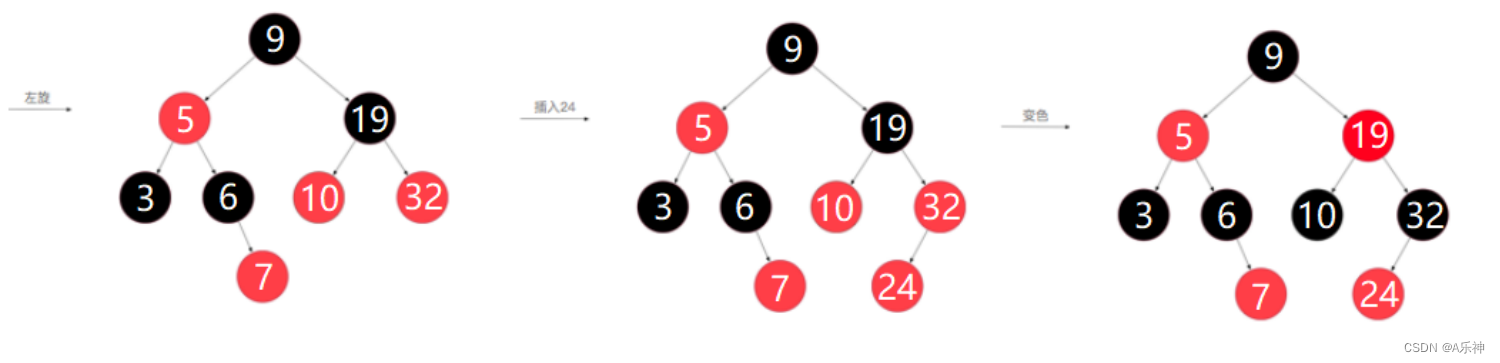
Java 数据结构 二叉树(二)红黑树
目录 数据结构图-树 简介 规则 旋转 重新着色 红黑树构建过程 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步…...

React18-完成弹窗封装
弹框封装 用法 // 创建 userRef.current?.open(create) // 修改 userRef.current?.open(edit,values){/* 创建用户 */} <CreateUser mRef{userRef} update{} />组件暴露open方法 文档地址:https://react.dev/reference/react/useImperativeHandle useIm…...

蓝桥杯2024/1/31-----底层测试模板
和之前一样建好工程文件夹,里边包含User(放工程文件,mian.c)、Driver(存放底层文件如Led.c,Led.h等) 新建的工程先搭建框架,可以先书写底层函数(此次书写了四个函数并包含…...
-高精度-乘-低精度)
蓝桥杯备战(AcWing算法基础课)-高精度-乘-低精度
目录 前言 1 题目描述 2 分析 2.1 关键代码 2.2 关键代码分析 3 代码 前言 详细的代码里面有自己的理解注释 1 题目描述 给定两个非负整数(不含前导 00) A 和 B,请你计算 AB 的值。 输入格式 共两行,第一行包含整数 A&a…...

C++设计模式-里氏替换原则
里氏替换原则定义了继承规范。(封装、继承、多态) 定义1:类型S对象o1,类型T对象o2,o1换成o2时程序意图不变,那么S是T的子类。 定义2:使用子类不破坏父类的意图。 注意:如果子类不…...

compose LazyColumn + items没有自动刷新问题
val dataLists by remember { mutableStateOf(datas) } 数据更改后列表不刷新问题。 val dataLists by remember { mutableStateOf(datas) } LazyColumn(modifier Modifier.padding(top 5.dp)) {items(dataLists) {....}} 可以将mutableStateOf 改为mutableStateListOf解决…...

Java八大常用排序算法
1冒泡排序 对于冒泡排序相信我们都比较熟悉了,其核心思想就是相邻元素两两比较,把较大的元素放到后面,在一轮比较完成之后,最大的元素就位于最后一个位置了,就好像是气泡,慢慢的浮出了水面一样 Jave 实现 …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
