《数电》理论笔记-第1章-逻辑代数基础
参考:视频 和 《数字电路与逻辑设计》
电子书
一,第1章 逻辑代数基础
1 数字量和模拟量
略
2 数制(十进制,二进制,八进制和十六进制)
拨电话(BoDH)---(2八10十六)进制
2.1 数制转化
2,8,16进制之间的转换
2,8,16进制和10进制的转换
3 代码
有权码和无权码区别是每一位是否有权值。
8421BCD码(有权码,数字码)
8421BCD码的“0111”,0×8+1×4+1×2+1×1=7D,其中D表示十进制(Decimal)数
格雷码(无权码,数字码)
略
ASCII码(无权码,字符码)
略
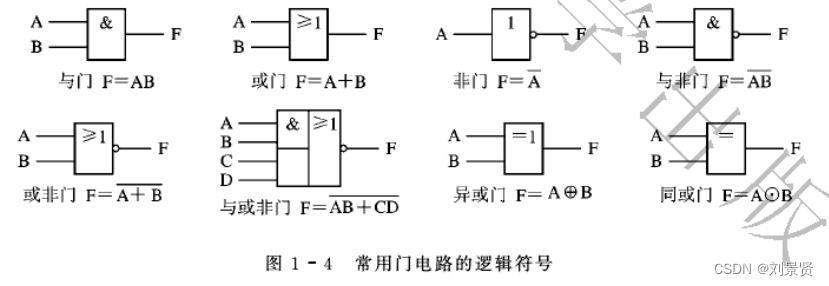
4 逻辑代数的基本运算和门电路
德摩根定理_德摩根公式
逻辑与(逻辑相乘)
全为1,输出才为1
逻辑或(逻辑相加)
全为0,输出才为0
逻辑非(逻辑反)
输出的是输入相反
其他
异或逻辑:输入相同为 0 ,相异为 1 同或逻辑:输入相同为 1 ,相异为
其他的略
门电路
5 逻辑代数的公式和规则
5.1基本公式
5.2 常用公式
5.2三个规则
1,带入规则

2,反演规则

3,对偶规则

6 逻辑函数常用描述方法
表达式、真值表、卡诺图和逻辑图
6.1 表达式
由逻辑变量和逻辑运算符号组成,表示变量之间逻辑关系
与或表达式、标准与或表达式、或与表达式、标准或与表达式、与非与非表达式、
或非或非表达式、与或非表达式等。
6.2 真值表
略
6.3 卡诺图
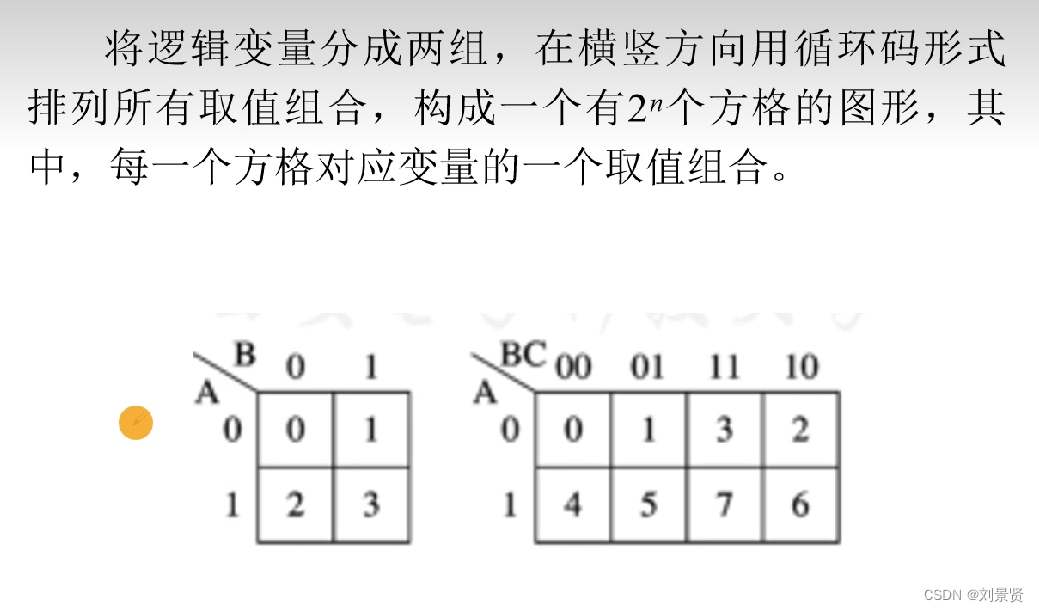
变量卡诺图,函数卡诺图
6.4 逻辑图
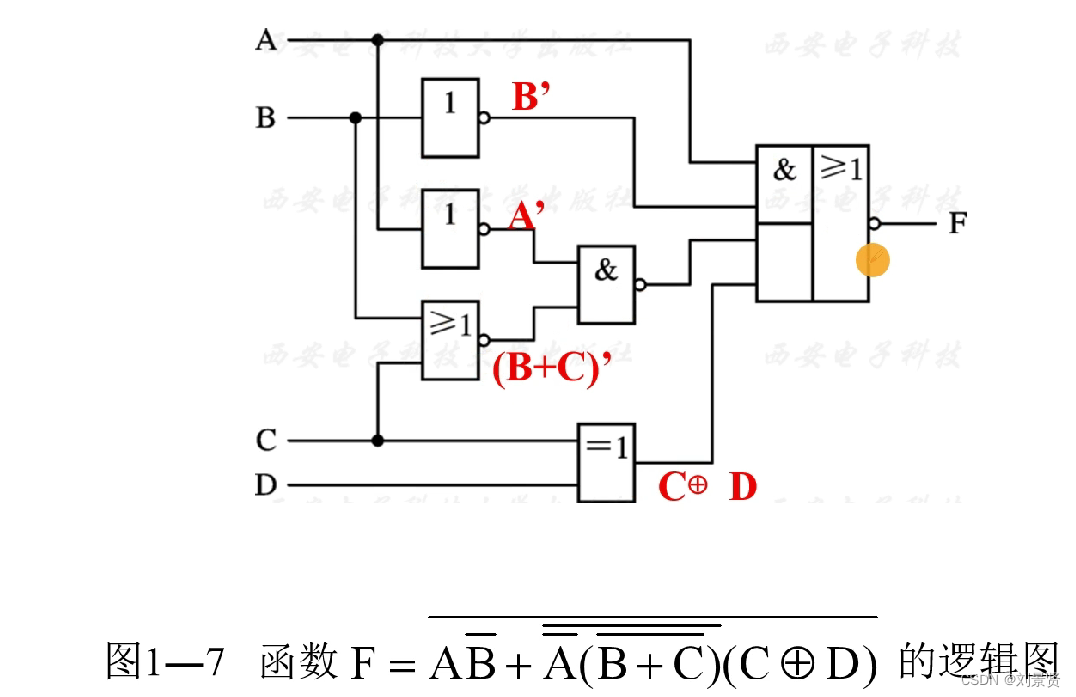
6.5 四种描述方法之间的转换
表达式和真值表转换
真值表和卡诺图转换
表达式和卡诺图转换
7 逻辑函数的化简
同一个逻辑函数可以写成不同表达式。用门电路去实现时,表达式越简单,
需用门电路个数就越少,越经济可靠。
因此,先化简,求出最简表达式,再去实现遇辑函数。
最常用的有 最简与或表达式 和 最简或与表达式

7.1公式法化简


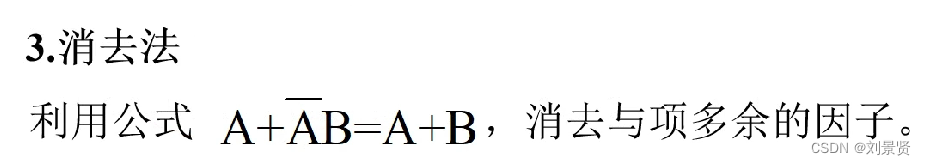
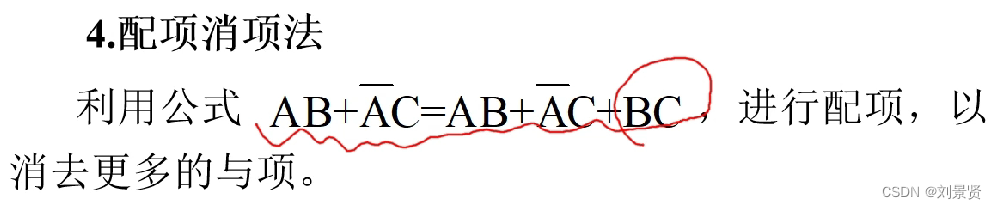
7.2卡诺图法化简
7.2.1求最简与或表达式
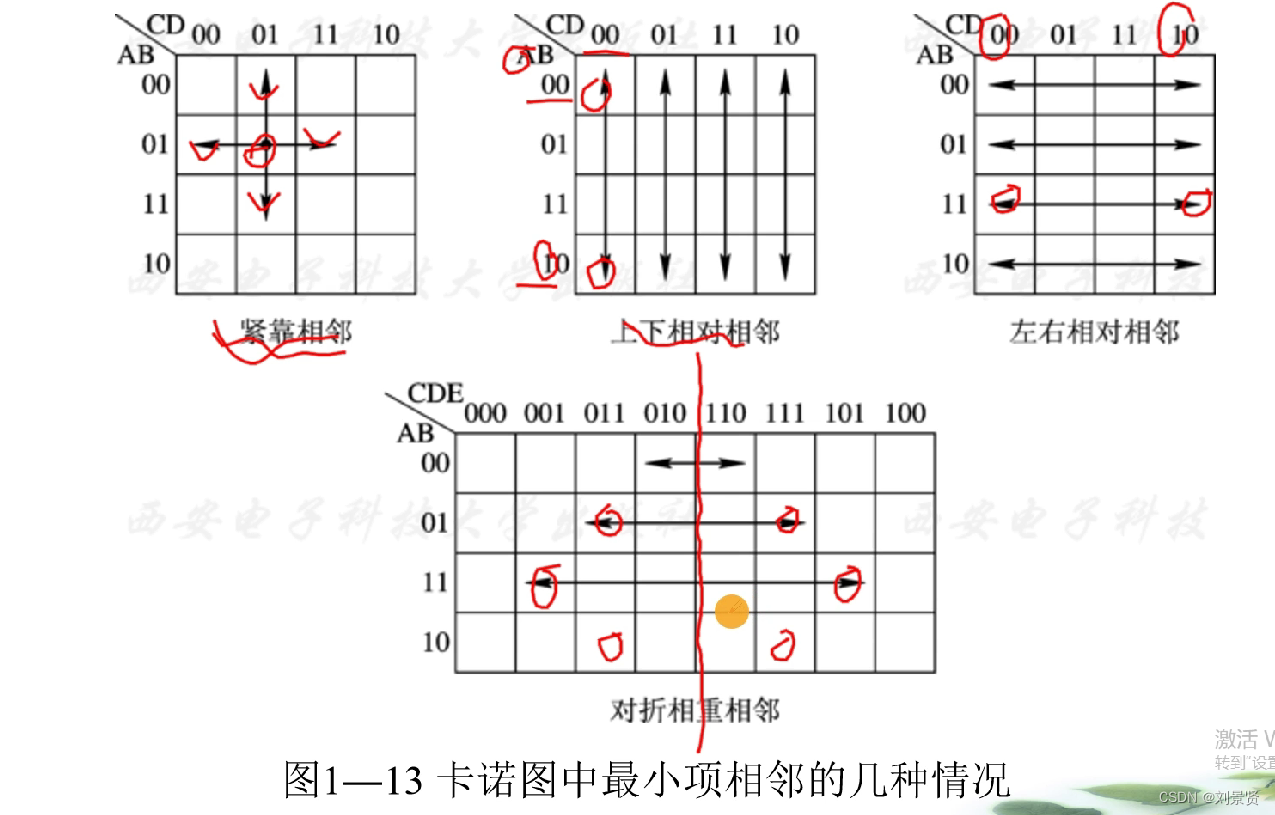
卡诺图的相邻性
最小项的相邻性定义:两个最小项,如果只有一个变量的形式不同(在一个最小项中以原变量出现,在另一个最小项中以反变量出现),其余变量的形式都不变,则称这两个最小项是逻辑相邻的。
相邻性判别: 在两个方格中,如果只有一个变量的取值不同(在一个方格中取1,在另一个方格中取0),这两个方格对应的最小项是逻辑相邻的。
化简方法:
卡诺图化简法的步骤和原则
1,画卡诺图。
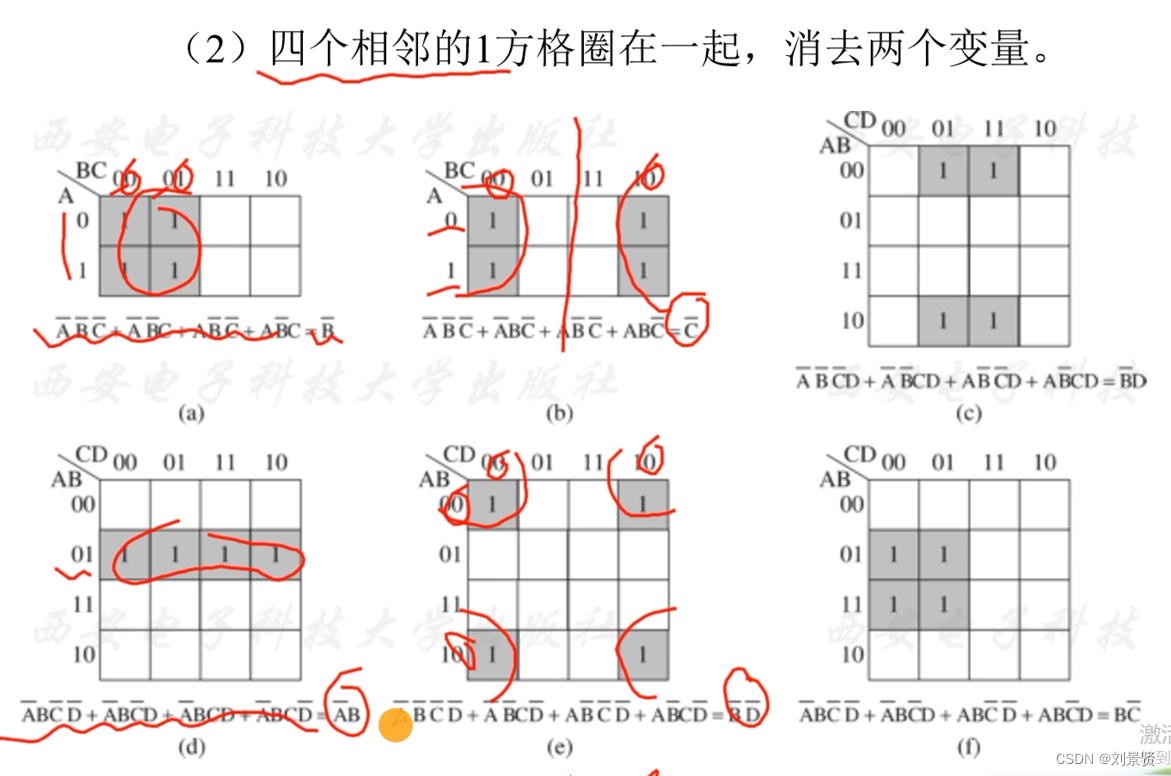
2,分组合并也就是画圈。
1)每个1至少被圈一次。
2)每个圈至少有一个1是其余所有圈中不包含的。如果任何一个1方格都出现在别的圈中,则这个圈就是多余的。
3)不能圈0。
4)圈的个数越少越好————得到的与项就越少。5)圈越大越好————消去的变量越多,所得与项包含的因子就越少。
每个圈中1方格的个数必须是2的整数次方。
3,写出最简与或表达式。
卡诺图化简法12分钟以后是例题
7.2.2 求最简或与表达式
求最简或与表达式,可以先求出其反函数的最简与或表达式,然后取反得到最简或与表达式。卡诺图中,函数值为0意味着反函数值为1,因此,利用卡诺图化简法求函数的最简或与表达式时,应对函数卡诺图中的0方格对应的最小项进行分组合并。
步骤:
1)画卡诺图。
2)对0方格对应最小项进行分组合并,求反函数的最简与或表达式。3)对反函数的最简与或表达式取反,得函数的最简或与表达式。
例题
8 带无关项逻辑函数的化简
8.1逻辑函数中的无关项
在实际的逻辑关系中,有时会遇到这样一种情况:即变量的某些取值组合是不会发生的,这种加给变量的限制称为变量的约束,而这些不会发生的组合所对应的最小项称为约束项。显然,对变量所有可能的取值,约束项的值都等于0.
8.2加入无关项简化化简
例题3分钟之后
没写例题和习题。。
相关文章:

《数电》理论笔记-第1章-逻辑代数基础
参考:视频 和 《数字电路与逻辑设计》 电子书 一,第1章 逻辑代数基础 1 数字量和模拟量 略 2 数制(十进制,二进制,八进制和十六进制) 拨电话(BoDH)---(2八10十六&…...

计算指定路径下的可用空间大小
方法一、使用psutil库 import psutildef check_disk_space(path):usage psutil.disk_usage(path)## 1GB 1 * 1024 * 1024 * 1024字节if usage.free > 1 * 1024 * 1024 * 1024:return 1else:return 0disk_path "/home" result check_disk_space(disk_path) pr…...

2023年全球软件架构师峰会(ArchSummit上海站):核心内容与学习收获(附大会核心PPT下载)
微服务架构是当今软件架构的主流趋势之一。随着云计算和分布式系统的普及,越来越多的企业开始采用微服务架构来构建他们的应用。微服务架构可以将一个大型的应用拆分成多个小型的服务,每个服务都独立部署、独立运行,并通过轻量级的通信协议进…...
)
踩坑实录(Second Day)
作为公司的小菜鸟,每天都踩坑应该是一件很正常的事情吧,哈哈哈。今天遇到了比较棘手的问题,以前从来没有遇到过。然后就是在某平台上接的一个 bug 修改的单子,也拿出来和大家分享一下~ 此为第二篇(2024 年 02 月 05 日…...

已解决org.springframework.web.HttpMediaTypeNotAcceptableException异常的正确解决方法,亲测有效!!!
已解决org.springframework.web.HttpMediaTypeNotAcceptableException异常的正确解决方法,亲测有效!!! 文章目录 问题分析 报错原因 解决思路 解决方法 总结 问题分析 在Spring MVC应用中处理HTTP请求时,我们有…...
根据MySql建表语句创建Java实体类工具
点击下载《根据MySql建表语句创建Java实体类工具》 1. 前言 在软件开发领域,特别是在构建企业级应用时,数据模型与代码模型之间的映射是至关重要的。该软件是一款基于C#开发的高效工具,它将这一繁琐且容易出错的过程变得简洁且快速。此工具…...
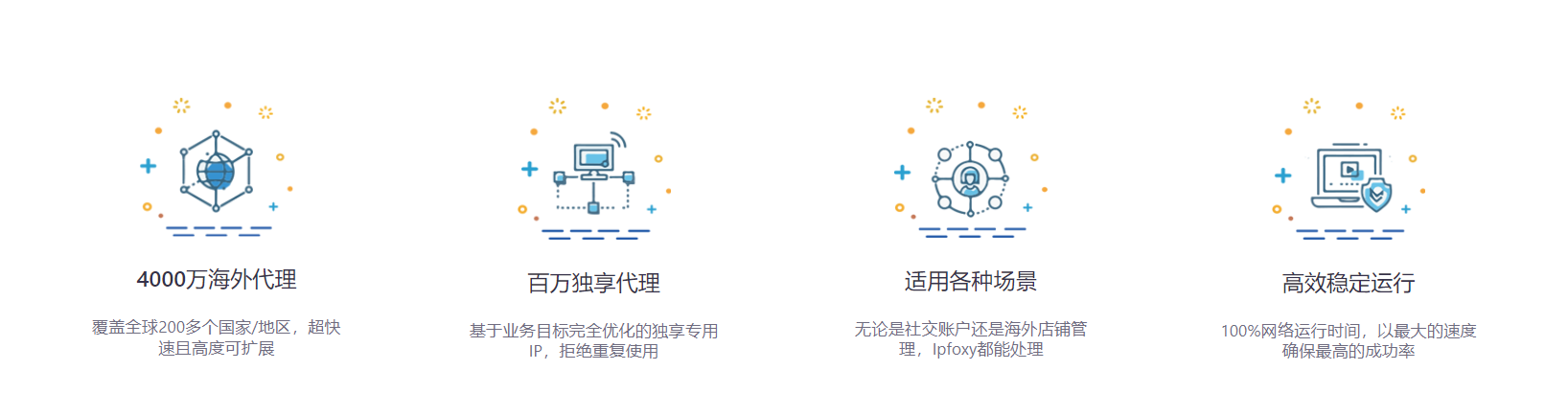
做跨境电商需要使用住宅代理IP吗?
住宅代理IP是近年来跨境电商领域日益受到重视的技术工具,不仅可以保护隐私、优化网络速度,还能助推跨境电商的精细化管理。接下来,我们将深入探讨利用住宅代理IP如何为跨境电商业务带来竞争优势。 一、住宅代理IP与跨境电商 住宅代理IP&…...

vue3 之 组合式API—reactive和ref函数
ref() 作用:接收简单类型或者对象类型的数据传入并返回一个响应式的对象 核心步骤: 1️⃣ 从 vue 包中导入 ref 函数 2️⃣在 <script setup>// 导入import { ref } from vue// 执行函数 传入参数 变量接收const count …...

Python库-PyAutoGUI
pyautogui是一个Python库,可以自动控制键盘和鼠标,非常适合进行自动化任务。它可以用于各种场景,比如自动化测试、数据录入任务,甚至是简单的游戏机器人。下面是一个关于pyautogui的入门教程,包括它的安装、基本使用方…...

越权测试是什么?
一、越权测试是什么? 越权漏洞是web应用程序中常见的一种安全漏洞。它的威胁在于一个账户可控制全站用户数据。越权漏洞产生的原因主要是因为开发人员在对数据进行增删改查时对客户端的请求数据过分相信而遗漏了权限的判定。 二、越权漏洞的分类 越权分为2种&…...
H5 简约四色新科技风引导页源码
H5 简约四色新科技风引导页源码 源码介绍:一款四色切换自适应现代科技风动态背景的引导页源码,源码有主站按钮,分站按钮2个,QQ联系站长按钮一个。 下载地址: https://www.changyouzuhao.cn/11990.html...

使用 VTK 中的单元定位器来查找最近的点
开发环境: Windows 11 家庭中文版Microsoft Visual Studio Community 2019VTK-9.3.0.rc0vtk-example demo解决问题:使用 VTK 中的单元定位器来查找最近的点 关键点: 创建了一个球体数据源,并使用它构建了一个单元定位器&#x…...
时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测
时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测 目录 时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现基于CNN-LST…...

Xcode 15 及以上版本:libarclite 库缺少问题
参考链接:Xcode 15 libarclite 缺失问题_sdk does not contain libarclite at the path /ap-CSDN博客 报错: SDK does not contain libarclite at the path /Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/lib/arc/libarcl…...

Spring设计模式之单例模式
文章目录 一、概述二、单例模式的优点三、Spring中的单例模式四、单例模式的实现方式五、总结 一、概述 单例模式是一种创建型设计模式,确保一个类只有一个实例,并提供一个全局访问点来获取该实例。在Spring框架中,单例模式是默认的Bean定义…...
Fink CDC数据同步(二)MySQL数据同步
1 开启binlog日志 2 数据准备 use bigdata; drop table if exists user;CREATE TABLE user(id INTEGER NOT NULL AUTO_INCREMENT,name VARCHAR(20) NOT NULL DEFAULT ,birth VARCHAR(20) NOT NULL DEFAULT ,gender VARCHAR(10) NOT NULL DEFAULT ,PRIMARY KEY(id) ); ALTER TA…...
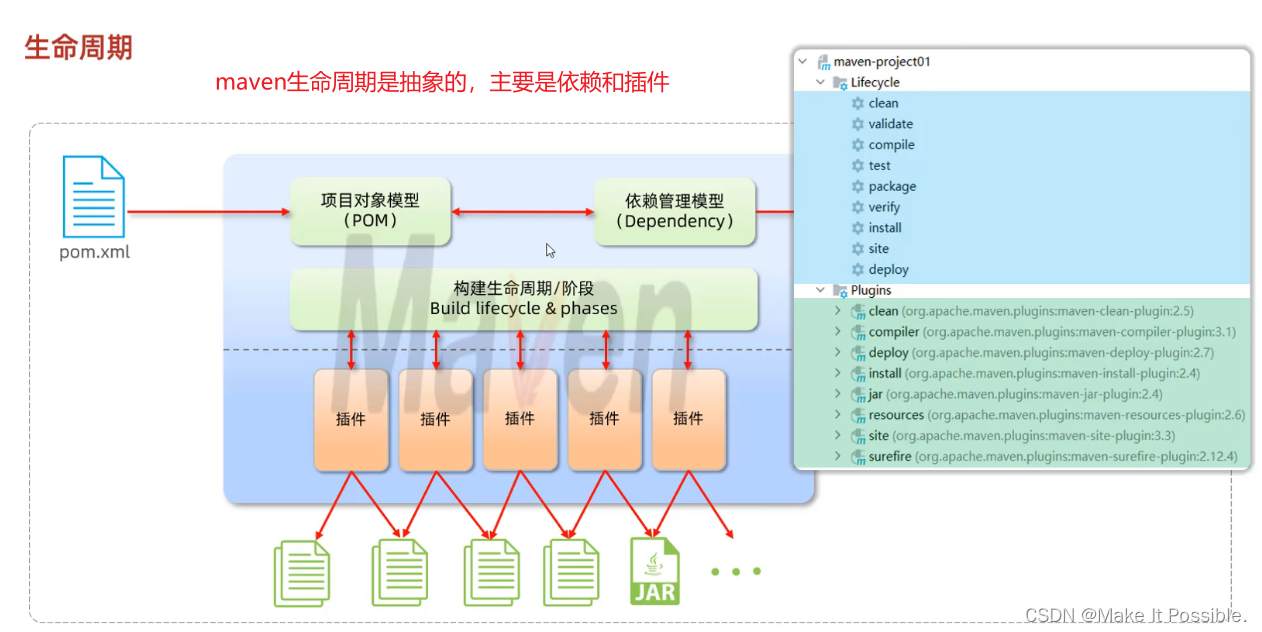
JavaWeb后端开发(第一期):Maven基础、Maven的安装配置、如何创建maven项目模块、maven的生命周期
Java后端开发:2024年2月6日 -> LiuJinTao 文章目录 JavaWeb后端开发(第一期) : maven基础一、 maven介绍1.1 什么maven呢:1.2 maven的作用1.3 maven 模型1.4 maven 仓库 二、maven 安装2.1 配置本地仓库2.2 配置阿里…...
鼠标和键盘消息处理)
Windows SDK(四)鼠标和键盘消息处理
鼠标基础知识 鼠标一般分为三种状态,三个按钮 三种状态:单击,双击,拖动 三个按钮:左键(LBUTTON),右键(RBUTTON),中键(MBUTTON&…...
LabVIEW汽车自燃监测预警系统
LabVIEW汽车自燃监测预警系统 随着汽车行业的飞速发展,汽车安全问题日益受到公众的关注。其中,汽车自燃现象因其突发性和破坏性,成为一个不可忽视的安全隐患。为了有效预防和减少自燃事故的发生,提出了LabVIEW的汽车自燃监测预警…...
数据图表方案,企业视频生产数据可视化
在信息爆炸的时代,如何将复杂的数据转化为直观、生动的视觉信息,是企业在数字化转型中面临的挑战。美摄科技凭借其独特的数据图表方案,为企业在数据可视化领域打开了一扇全新的大门。 一、数据图表方案的优势 1、高效便捷:利用数…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...