决策树的相关知识点
📕参考:ysu老师课件+西瓜书
1.决策树的基本概念

【决策树】:决策树是一种描述对样本数据进行分类的树形结构模型,由节点和有向边组成。其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。
理解:它是一个树状结构,其中每个节点代表一个特征属性的判断,每个分支代表这个判断的结果,而每个叶节点(叶子)代表一种类别或回归值。
关于决策树要掌握的概念:
根节点(Root Node): 包含整个数据集,并通过某个特征属性进行判断。
分支(Branch): 从根节点出发的每个路径,代表在某个特征属性上的判断结果。
内部节点(Internal Node): 在决策路径上的非叶节点,表示对某个特征属性的判断。
叶节点(Leaf Node): 在决策路径上的末端节点,表示最终的类别或回归值。
决策树的优缺点:
优点:
易于理解和解释: 决策树的图形化表示使得结果容易理解,可以可视化地表示整个决策过程。
无需特征缩放: 不需要对特征进行标准化或归一化。
处理混合数据类型: 可以处理既有连续型特征又有离散型特征的数据。
能够捕捉特征之间的相互关系: 可以捕捉特征之间的非线性关系。
缺点:
过拟合(Overfitting): 在处理复杂问题时容易生成过于复杂的树,导致在训练数据上表现良好但在未知数据上泛化能力差。
对噪声敏感: 对数据中的噪声和异常值较为敏感。
不稳定性: 数据的小变化可能导致生成完全不同的树。
2.决策树的生成过程
决策树模型涉及到三个关键过程:
一是特征变量的选择,根据某个指标(如信息增益、基尼指数等)选择当前最佳的特征属性作为判断依据。
二是决策树的生成,常用的决策树算法有ID3、C4.5、CART等算法;
三是决策树的剪枝,通过剪枝来避免过拟合,提升对数据的预测效果。
2.1 特征变量的选择
最常用的三种特征选择策略:信息增益、信息增益比、Gini指数
2.1.1 信息增益
首先引入【信息量】。
消息中所包含的信息量大小与该消息所表示的事件出现的概率相关,如果一个消息所表示的事件是必然事件(发生概率100%),则该消息所包含的信息量为0;如果一个消息表示的不可能事件(发生概率极低),则该消息的信息量为无穷大。
比如:某同事跑过来和你说:“小王,明早太阳会从东方升起”。(概率为1,信息量为0)
信息量应该随着概率单调递减:某事件的概率越大,则信息量越小。
再引入【信息熵】。
“信息熵”用来表示信息不确定性的一种度量。熵越高表示越混乱,熵越低表示越有序。
(类比高中学的分子状态混乱程度,熵越大越混乱)
再引入【信息增益】。
“信息增益”表示在知道某个特征之后使得不确定性减少的程度(知道某个特征前的熵与知道某个特征之后的熵之差)。
根据某个变量将样本数据分割为多个子集,分割前与分割后样本数据的熵之差为信息增益,信息增益越高,表示该变量对样本数据的分类效果越好。
2.1.2 信息增益比
再引入【信息增益比】
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题,因此通过引入了【信息增益比】来解决该问题。
比如:以user_id为特征变量,由于每个人的user_id是唯一的,在每个user_id下可以完美地进行准确分类,但是这种情况显然是无意义的。

注:只有在不同变量分裂出不同个数子节点的情况下,信息增益比才会起作用。如果每个变量允许分裂相同个数的子节点,那么信息增益比并不起作用。
2.1.3 Gini指数
Gini指数也是衡量随机变量不纯度的一种方法,Gini指数越小,则表示变量纯度越高,Gini指数越大,表示变量纯度越低。

理解:
Gini指数表示在样本集合中随机抽取两个样本,其类别不一致的概率。因此Gini指数越小,分类越纯。
2.2 决策树的生成
常用的决策树算法有:ID3、C4.5、CART
先介绍决策树生成时的三个【终止条件】:
- 当前节点包含的样本全部属于同一类别
- 当前节点已经没有样本,不能再继续划分
- 所有特征已经使用完毕
2.2.1 ID3——信息增益
ID3(Iterative Dichotomiser 3)是一种基于信息增益的决策树生成算法。
其主要步骤包括:
计算信息熵: 对每个特征计算数据集的信息熵,用于度量数据的不确定性。
计算信息增益: 对每个特征计算信息增益,选择信息增益最大的特征作为当前节点的划分特征。
划分数据集: 使用选择的最佳特征对数据集进行划分,生成相应的子集。
递归生成子树: 对每个子集递归地应用上述步骤,生成子树。
停止条件: 在递归生成子树的过程中,设置停止条件,例如树的深度达到预定值、节点包含的样本数小于某个阈值等。
【专业描述】

2.2.2 C4.5——信息增益比
C4.5算法整体上与ID3算法非常相似,不同之处是C4.5以信息增益比为准则来选择分枝变量。
2.2.3 CART——Gini指数
CART(Classification and Regression Trees)是一种基于Gini指数的决策树生成算法,可用于分类和回归任务。
其主要步骤包括:
计算Gini指数: 对每个特征计算数据集的Gini指数,用于度量数据的不纯度。
选择最小Gini指数的特征: 选择Gini指数最小的特征作为当前节点的划分特征。
划分数据集: 使用选择的最佳特征对数据集进行划分,生成相应的子集。
递归生成子树: 对每个子集递归地应用上述步骤,生成子树。
停止条件: 在递归生成子树的过程中,设置停止条件,例如树的深度达到预定值、节点包含的样本数小于某个阈值等。
【专业描述】

注意:
CART是一种二叉树,即将所有问题看做二元分类问题。
由于CART是二叉树,在遇到连续变量或者多元分类变量时,存在寻找最优切分点的情况。
【补充】
CART的缺点
二元划分: CART算法每次划分只能选择一个特征的一个切分点进行二元划分,这可能导致树的结构相对较深,对某些问题可能不够简洁。
贪婪算法: CART是一种贪婪算法,它在每一步选择最优划分,但这并不一定会导致全局最优的决策树。有时候,全局最优的决策树需要考虑多步划分的组合,而CART只考虑当前最优的一步。
对于不平衡数据集的处理: 在处理不平衡数据集时,CART可能会偏向那些具有较多样本的类别,导致对于少数类的划分不够精细。
非平滑性: CART生成的树是非平滑的,对于输入空间的微小变化可能产生较大的输出变化,这使得CART对于输入空间的局部变化较为敏感。
两种决策的对比
信息增益(ID3): 用于分类问题,通过选择能够最大程度降低不确定性的特征。
基尼不纯度(CART): 适用于分类和回归问题,通过选择能够最小化不纯度的特征。
2.3 决策树的剪枝
决策树的剪枝是为了防止过拟合,即过度依赖训练数据而导致在未知数据上表现不佳。
剪枝通过修剪决策树的一部分来达到简化模型的目的。
剪枝分为预剪枝(Pre-pruning)和后剪枝(Post-pruning)两种类型。
2.3.1 预剪枝
在决策树生成的过程中,在每次划分节点之前,通过一些预定的规则判断是否继续划分。若当前结点的划分不能使决策树泛化性能提升,则停止划分并将当前结点记为叶结点,其类别标记为训练样例数最多的类别。
预剪枝的一些常见条件包括:
- 树的深度限制: 设置树的最大深度,防止树过于复杂。
- 节点样本数量限制: 当节点中的样本数量小于某个阈值时停止划分。
- 信息增益或基尼不纯度阈值: 当划分节点后的信息增益或基尼不纯度低于设定的阈值时停止划分。
预剪枝的优缺点
优点:
- 降低过拟合风险
- 显著减少训练时间和测试时间开销
缺点:
- 欠拟合风险:有些分支的当前划分虽然不能提升泛化性能,但在其基础上进行的后续划分却有可能导致性能显著提高。预剪枝基于“贪心”本质禁止这些分支展开,带来了欠拟合风险
2.3.2 后剪枝
在决策树生成完成后,通过递归地从底部向上对节点进行判断,决定是否剪枝。
具体过程如下:
从叶子节点开始: 递归地向上考察每个叶子节点。
计算剪枝前后的性能: 对于每个叶子节点,计算剪枝前后在验证集上的性能差异。
剪枝决策: 如果剪枝可以提高性能(如准确率、F1分数等),则进行剪枝,将该节点变为叶子节点。
重复: 重复上述过程,直到找到合适的剪枝点或不再发生性能提升。
后剪枝相对于预剪枝更为灵活,因为它在生成完整的树之后才进行剪枝决策,可以更准确地评估每个子树的性能。
后剪枝的优缺点:
优点:
- 后剪枝比预剪枝保留了更多的分支,欠拟合风险小,泛化性能往往优于预剪枝决策树
缺点
- 训练时间开销大:后剪枝过程是在生成完全决策树之后进行的,需要自底向上对所有非叶结点逐一考察
3.代码实践
# 导入必要的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_text
from sklearn import tree
import matplotlib.pyplot as plt# 加载示例数据集(鸢尾花数据集)
iris = load_iris()
X = iris.data
y = iris.target# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建决策树模型
clf = DecisionTreeClassifier()# 训练模型
clf.fit(X_train, y_train)# 使用模型进行预测
y_pred = clf.predict(X_test)# 输出模型的准确率
accuracy = clf.score(X_test, y_test)
print(f"Model Accuracy: {accuracy:.2f}")# 输出决策树的规则
tree_rules = export_text(clf, feature_names=iris.feature_names)
print("Decision Tree Rules:\n", tree_rules)# 可视化决策树
fig, ax = plt.subplots(figsize=(12, 8))
tree.plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, ax=ax)
plt.show()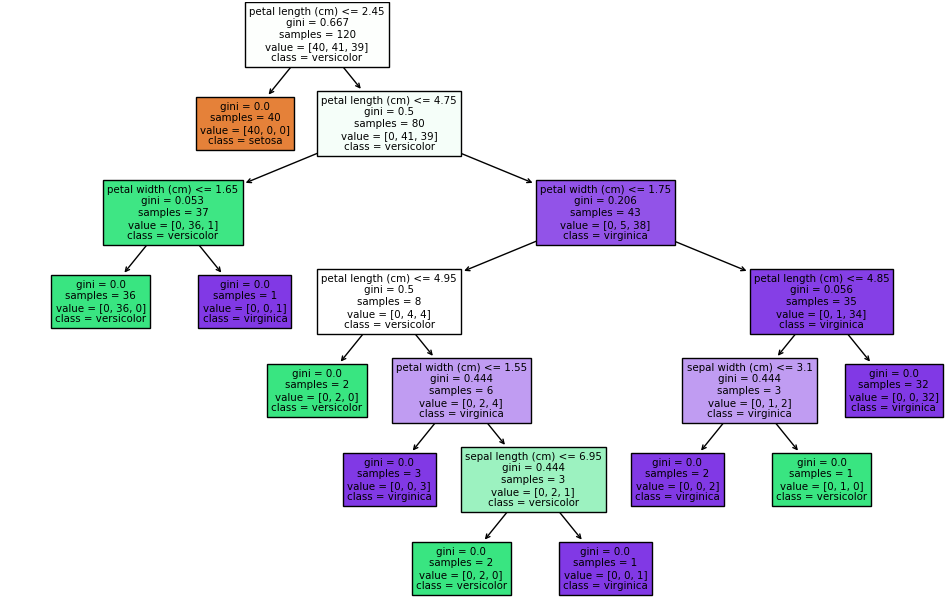
相关文章:

决策树的相关知识点
📕参考:ysu老师课件西瓜书 1.决策树的基本概念 【决策树】:决策树是一种描述对样本数据进行分类的树形结构模型,由节点和有向边组成。其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出ÿ…...
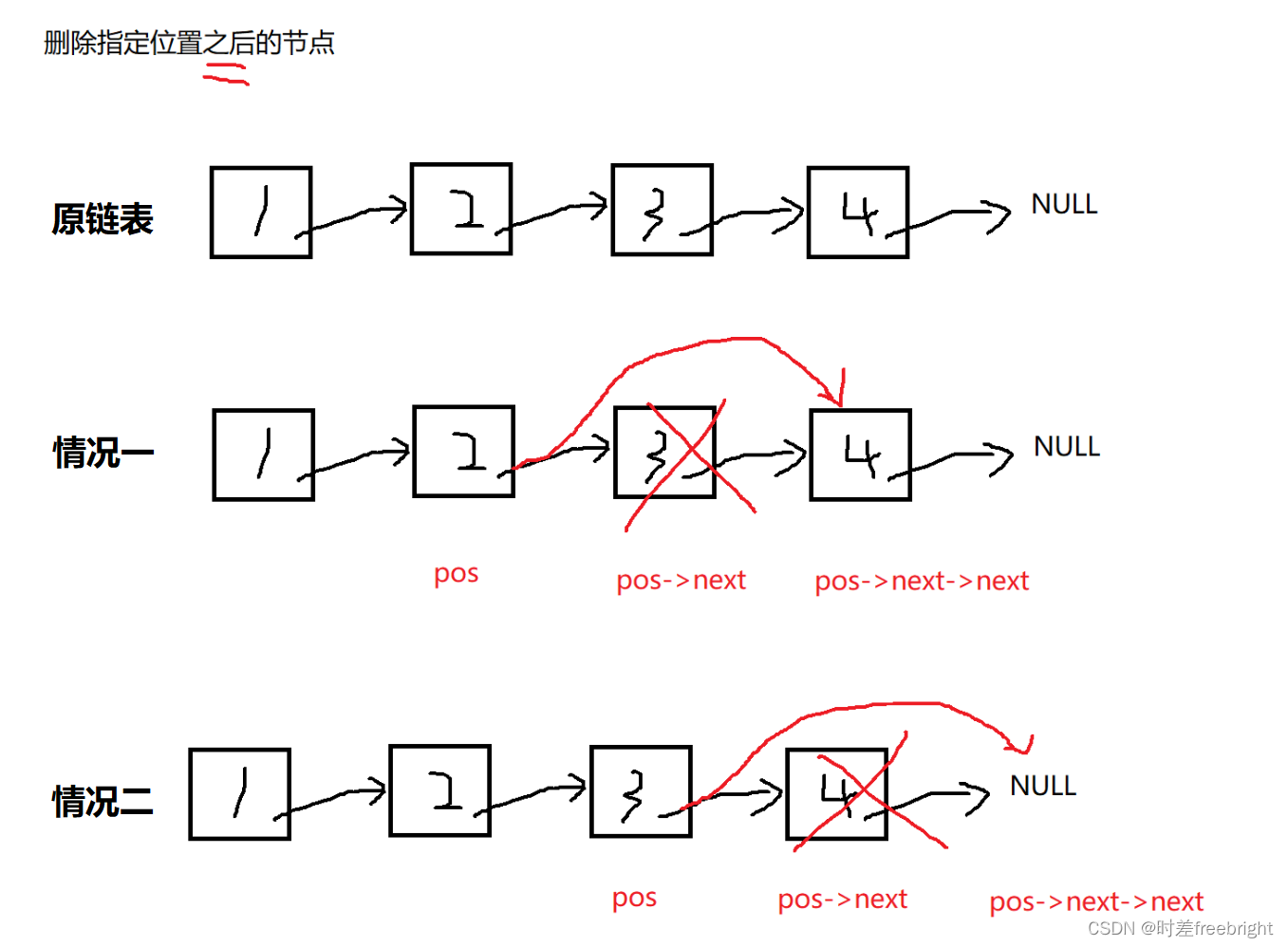
【数据结构】单向链表实现 超详细
目录 一. 单链表的实现 1.准备工作及其注意事项 1.1 先创建三个文件 1.2 注意事项:帮助高效记忆和理解 2.链表的基本功能接口 2.0 创建一个 链表 2.1 链表的打印 3.链表的创建新节点接口 4.链表的节点插入功能接口 4.1 尾插接口 4.2 头插接口 4.3 指定位…...

Opencc4j 开源中文繁简体使用介绍
Opencc4j Opencc4j 支持中文繁简体转换,考虑到词组级别。 Features 特点 严格区分「一简对多繁」和「一简对多异」。 完全兼容异体字,可以实现动态替换。 严格审校一简对多繁词条,原则为「能分则不合」。 词库和函数库完全分离,…...

vue 下载二进制文件
文章目录 概要技术细节 概要 vue 下载后端返回的二进制文件流 技术细节 import axios from "axios"; const baseUrl process.env.VUE_APP_BASE_API; //downLoadPdf("/pdf/download?pdfName" res .pdf, res); export function downLoadPdf(str, fil…...

数据结构之堆排序
对于几个元素的关键字序列{K1,K2,…,Kn},当且仅当满足下列关系时称其为堆,其中 2i 和2i1应不大于n。 { K i ≤ K 2 i 1 K i ≤ K 2 i 或 { K i ≥ K 2 i 1 K i ≥ K 2 i {\huge \{}^{K_i≤K_{2i}} _{K_i≤K_{2i1}} …...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之ScrollBar组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之ScrollBar组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、ScrollBar组件 鸿蒙(HarmonyOS)滚动条组件ScrollBar&…...
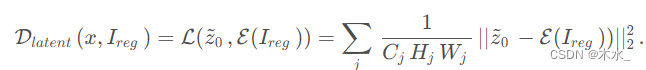
读论文:DiffBIR: Towards Blind Image Restoration with Generative Diffusion Prior
DiffBIR 发表于2023年的ICCV,是一种基于生成扩散先验的盲图像恢复模型。它通过两个阶段的处理来去除图像的退化,并细化图像的细节。DiffBIR 的优势在于提供高质量的图像恢复结果,并且具有灵活的参数设置,可以在保真度和质量之间进…...
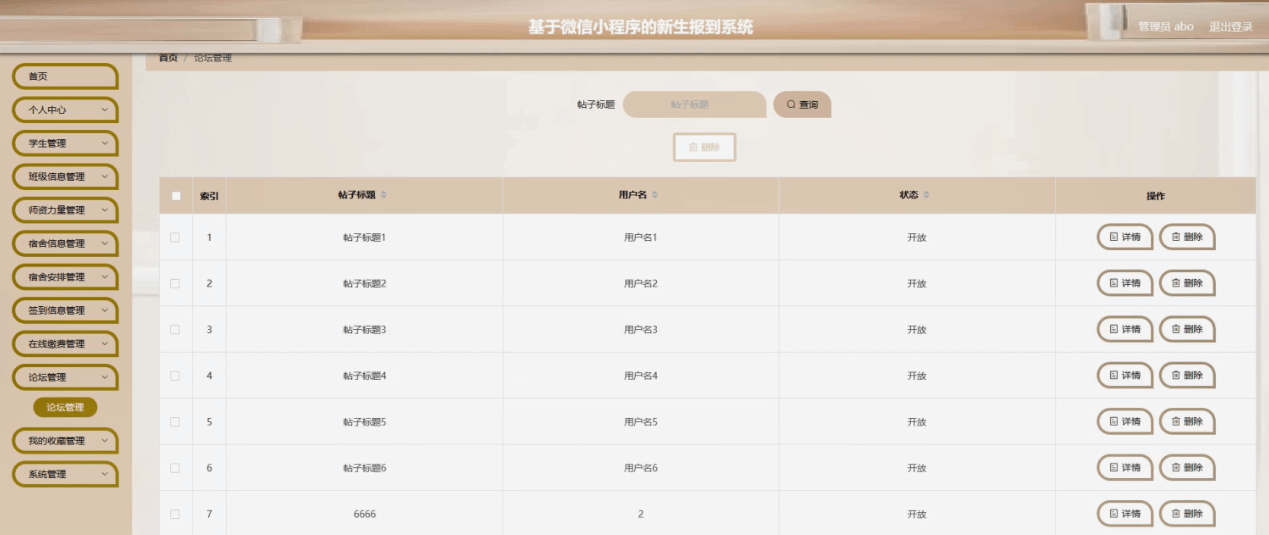
基于微信小程序的新生报到系统的研究与实现,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
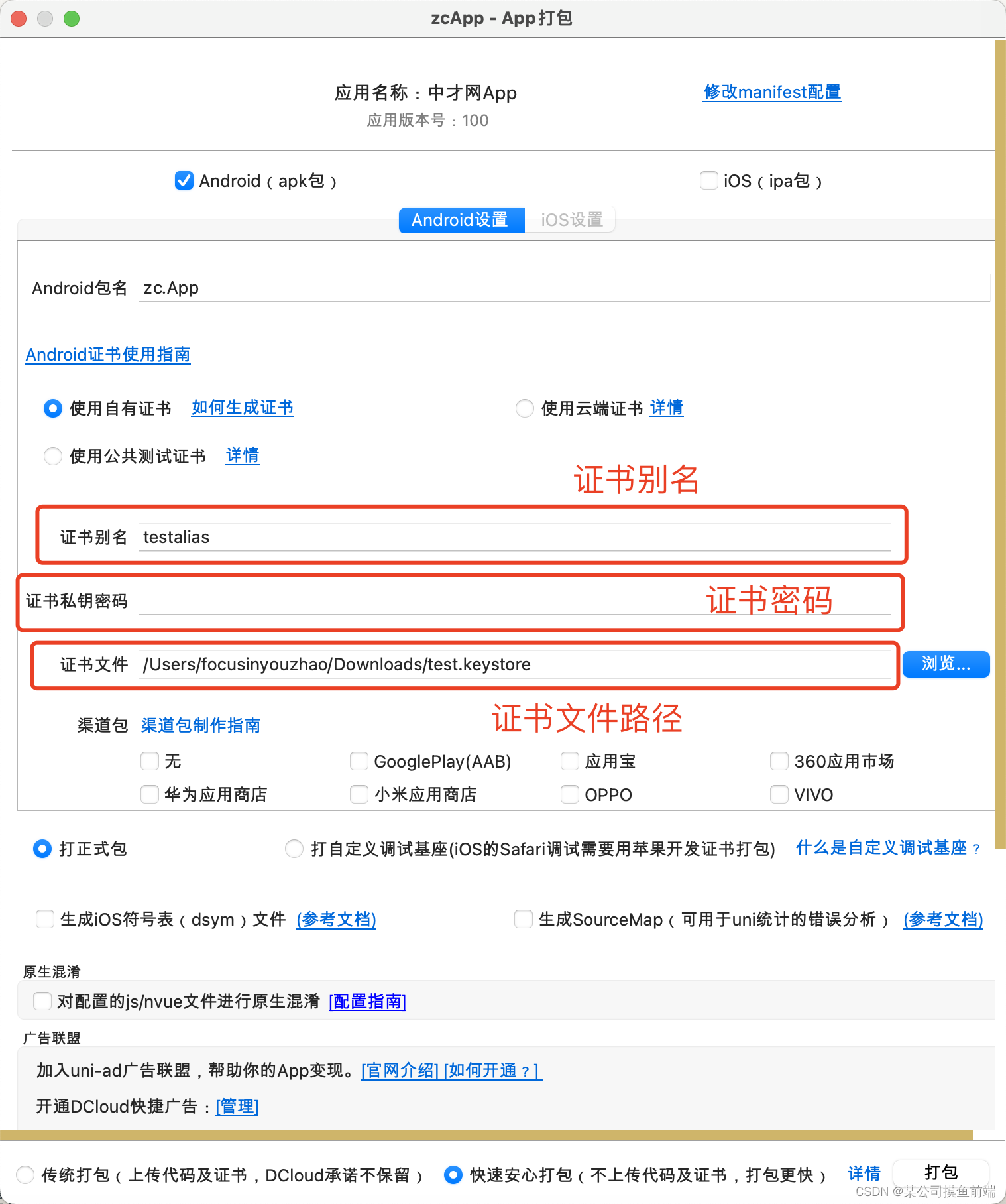
分享一下 uniapp 打包安卓apk
首先需要安装 Java 环境,这里就不做解释了 第二步:打开 mac 终端 / cmd 命令行工具 使用keytool -genkey命令生成证书 keytool -genkey -alias testalias -keyalg RSA -keysize 2048 -validity 36500 -keystore test.keystore *testalias 是证书别名&am…...
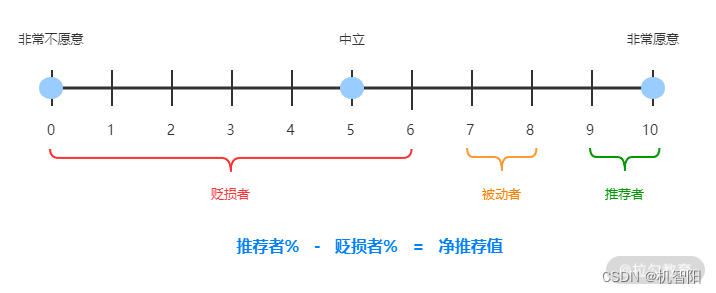
DevOps落地笔记-21|业务价值:软件发布的最终目的
上一课时介绍如何度量软件的内部质量和外部质量。在外部质量中,我们提到用户满意度是衡量软件外部质量的关键因素。“敏捷宣言”的第一条原则规定:“我们最重要的目标,是通过持续不断的及早交付有价值的软件使用户满意”。从这一点也可以看出…...

【动态规划】【前缀和】【数学】2338. 统计理想数组的数目
作者推荐 【动态规划】【前缀和】【C算法】LCP 57. 打地鼠 本文涉及知识点 动态规划汇总 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 LeetCode:2338. 统计理想数组的数目 给你两个整数 n 和 maxValue ,用于描述一个 理想…...

【已解决】onnx转换为rknn置信度大于1,图像出现乱框问题解决
前言 环境介绍: 1.编译环境 Ubuntu 18.04.5 LTS 2.RKNN版本 py3.8-rknn2-1.4.0 3.单板 迅为itop-3568开发板 一、现象 采用yolov5训练并将pt转换为onnx,再将onnx采用py3.8-rknn2-1.4.0推理转换为rknn出现置信度大于1,并且图像乱框问题…...
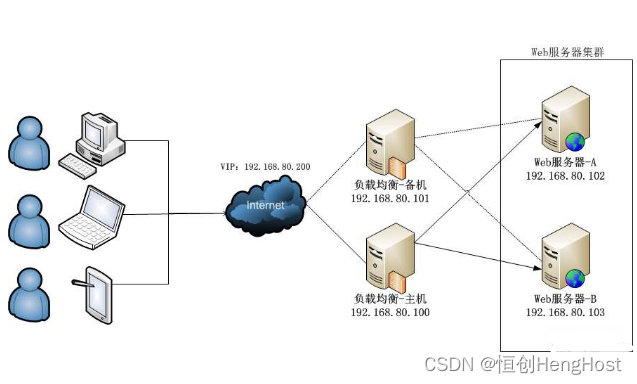
多路服务器技术如何处理大量并发请求?
在当今的互联网时代,随着用户数量的爆炸性增长和业务规模的扩大,多路服务器技术已成为处理大量并发请求的关键手段。多路服务器技术是一种并行处理技术,它可以通过多个服务器同时处理来自不同用户的请求,从而显著提高系统的整体性…...

SpringBoot - 不加 @EnableCaching 标签也一样可以在 Redis 中存储缓存?
网上文章都是说需要在 Application 上加 EnableCaching 注解才能让缓存使用 Redis,但是测试发现不用 EnableCaching 也可以使用 Redis,是网上文章有问题吗? 现在 Application 上用了 EnableAsync,SpringBootApplication࿰…...
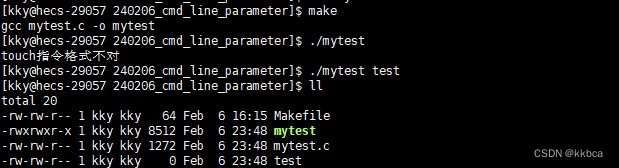
Linux------命令行参数
目录 前言 一、main函数的参数 二、命令行控制实现计算器 三、实现touch指令 前言 当我们在命令行输入 ls -al ,可以查看当前文件夹下所有文件的信息,还有其他的如rm,touch等指令,都可以帮我们完成相应的操作。 其实运行这些…...
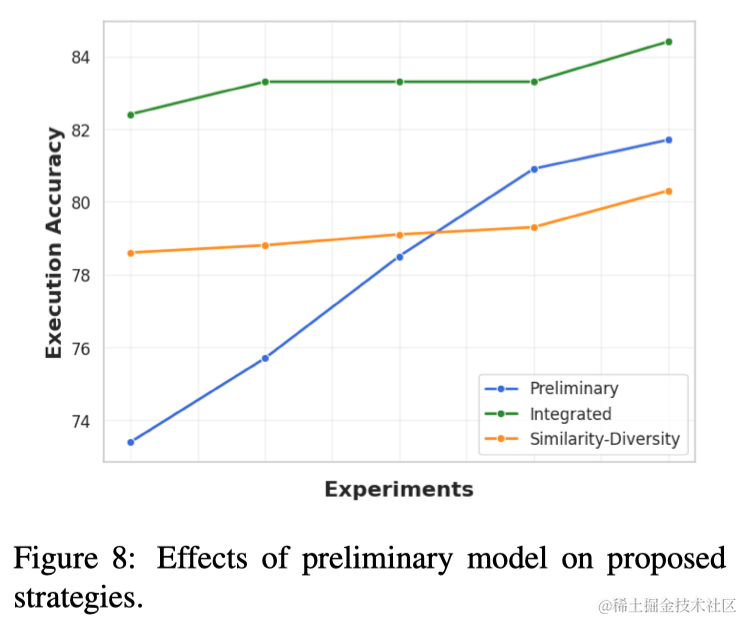
LLM少样本示例的上下文学习在Text-to-SQL任务中的探索
导语 本文探索了如何通过各种提示设计策略,来增强大型语言模型(LLMs)在Few-shot In-context Learning中的文本到SQL转换能力。通过使用示例SQL查询的句法结构来检索演示示例,并选择同时追求多样性和相似性的示例可以提高性能&…...
双非本科准备秋招(19.2)—— 设计模式之保护式暂停
一、wait & notify wait能让线程进入waiting状态,这时候就需要比较一下和sleep的区别了。 sleep vs wait 1) sleep 是 Thread 方法,而 wait 是 Object 的方法 2) sleep 不需要强制和 synchronized 配合使用,但 wait 强制和 s…...

使用SpringMVC实现功能
目录 一、计算器 1、前端页面 2、服务器处理请求 3、效果 二、用户登陆系统 1、前端页面 (1)登陆页面 (2)欢迎页面 2、前端页面发送请求--服务器处理请求 3、效果 三、留言板 1、前端页面 2、前端页面发送请求 &…...

spring aop实现接口超时处理组件
文章目录 实现思路实现代码starter组件 实现思路 这里使用FutureTask,它通过get方法以阻塞的方式获取执行结果,并设定超时时间: public V get() throws InterruptedException, ExecutionException ;public V get(long timeout, TimeUnit un…...
c++设计模式之装饰器模式
作用 为现有类增加功能 案例说明 class Car { public:virtual void show()0; };class Bmw:public Car { public:void show(){cout<<"宝马汽车>>"<<endl;} };class Audi:public Car { public:void show(){cout<<"奥迪汽车>>&q…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
