leetcode 算法 69.x的平方根(python版)
需求
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
分析
可以使用二分查找的思路来求解算术平方根。
首先,设定搜索范围,最小值为0,最大值为x。
然后,通过二分查找的方式逼近算术平方根。
每次选取中间值mid,计算mid的平方。如果平方小于等于x,说明mid可能是答案的一部分,更新最小值为mid,继续搜索mid右边的范围。
如果mid的平方大于x,说明mid不是答案的一部分,更新最大值为mid。
当搜索范围缩小到最小值和最大值相等时,返回最小值即可。
代码
class Solution:def x_sqrt(self,x):left=0right=xwhile left<=right:mid=(left+right)//2if mid*mid <= x <(mid+1)*(mid+1):return midelif mid*mid<x:left=mid+1else:right=mid-1if __name__ == '__main__':call=Solution()x=8print(call.x_sqrt(x))
运行结果
相关文章:

leetcode 算法 69.x的平方根(python版)
需求 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1&#…...

【golang】24、go get 和 go mod:indrect 与 go mod tidy
文章目录 go get 会执行如下操作: 操作 go.mod 文件(add、update、remove)下载依赖到 $GOPATH/pkg/mod 中若已安装,则更新该包,到最新版本 试验前置准备:首先删除已下载的依赖,rm -rf $GOPATH…...

AI算法工程师-非leetcode题目总结
AI算法工程师-非leetcode题目总结 除了Leetcode你还需要这些实现nms旋转矩形IOU手动实现BN手动实现CONV实现CrossEntropyLoss 除了Leetcode你还需要这些 希望大家留言,我可以进行补充。持续更新~~~ 实现nms import numpy as np def nms(dets, threshold):x1 dets…...
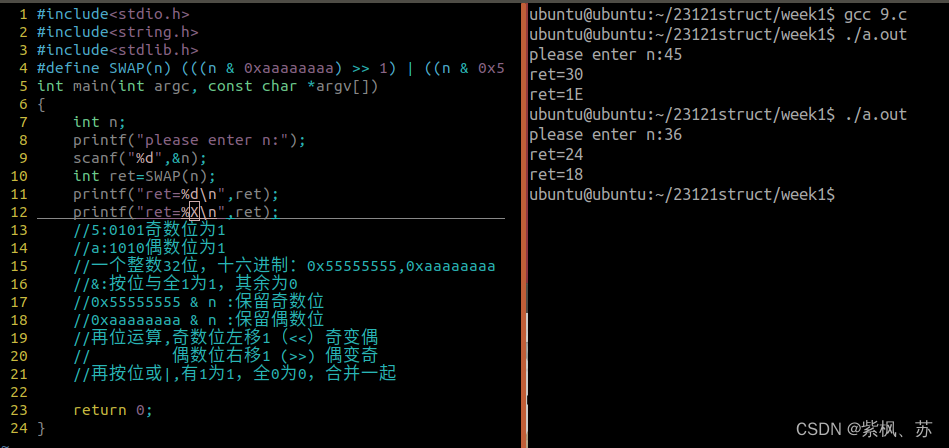
2.6:冒泡、简选、直插、快排,递归,宏
1.冒泡排序、简单选择排序、直接插入排序、快速排序(升序) 程序代码: 1 #include<stdio.h>2 #include<string.h>3 #include<stdlib.h>4 void Bubble(int arr[],int len);5 void simple_sort(int arr[],int len);6 void insert_sort(int arr[],in…...
FastDFS安装并整合Openresty
FastDFS安装并整合Openresty 一、安装环境准备【CentOS7.9】二、FastDFS--tracker安装2.1.下载fastdfs2.2.FastDFS安装环境2.3.安装FastDFS依赖libevent库2.4.安装libfastcommon2.5.安装 libserverframe 网络框架2.6.tracker编译安装2.7.安装之后文件目录介绍2.8.错误处理2.9.配…...
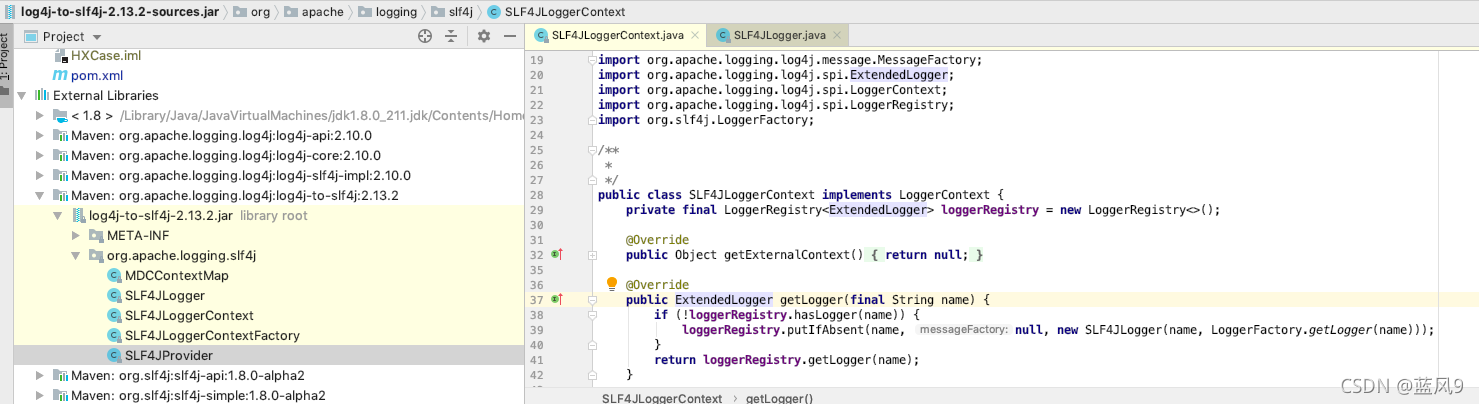
93 log4j-slf4j-impl 搭配上 log4j-to-slf4j 导致的 StackOverflow
前言 呵呵 最近想要 做一个 mongo 低版本的客户端读取高版本的服务端传递过来的数据造成的一个错误的时候, 出现了这样的问题 引入了 mongo-java-driver 之后, 使用相关 api 的时候会触发 com.mongo.internal.connection.BaseCluser 的初始化, 其依赖的 Loggers 间接的依赖…...
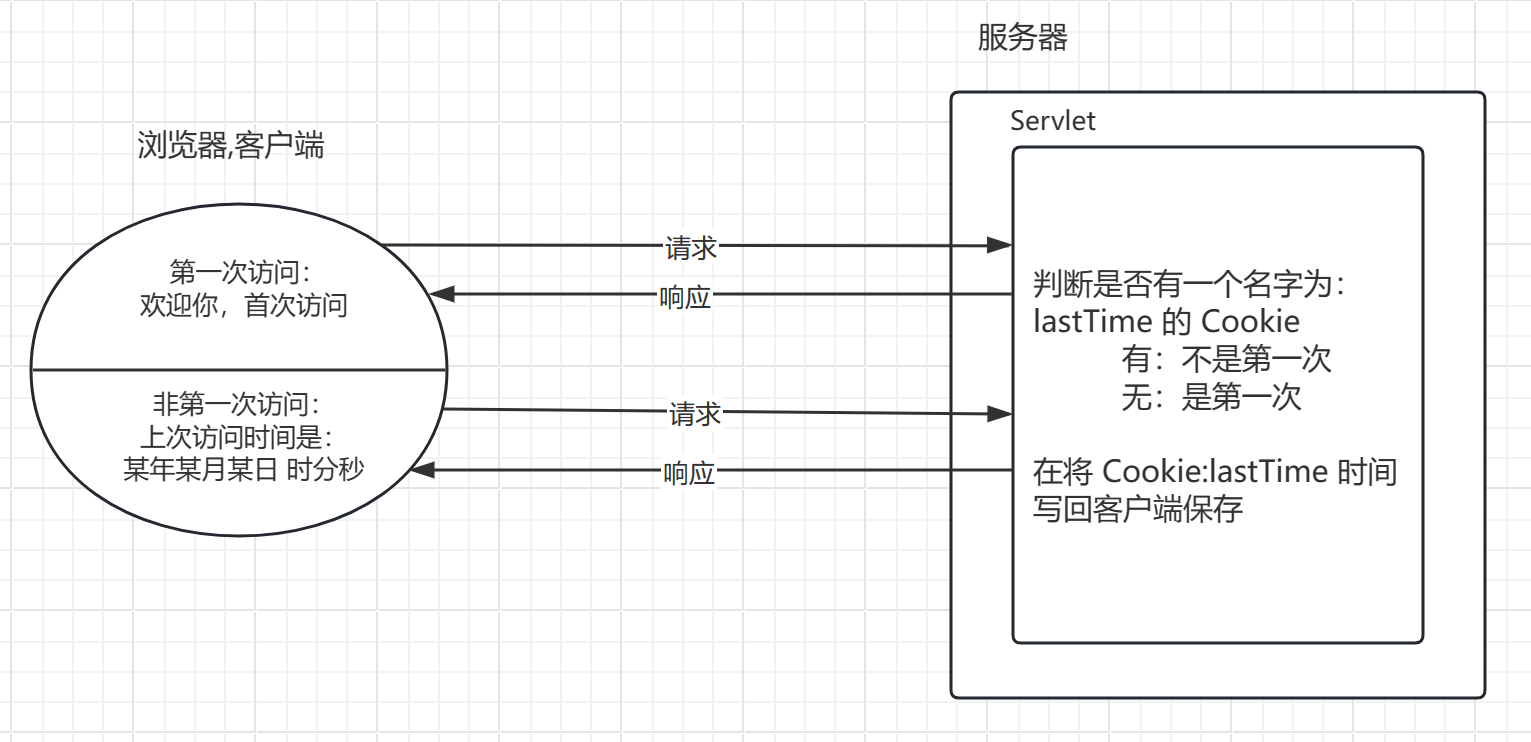
客户端会话技术-Cookie
一、会话技术 1.1 概述 会话:一次会话中包含多次**请求和响应** 一次会话:浏览器第一次给服务器资源发送请求,此时会话建立,直到有一方断开为止 会话的功能:在一次会话的范围内的多次请求间,共享数据 …...

rsa加密登录解决方案
1.问题 账密登录方式中用户输入密码后,把账号、密码通过http传输到后端进行校验,然而密码属于敏感信息,不能以明文传输,否则容易被拦截窃取,因此需要考虑如何安全传输密码 2.解决方案 使用rsa加密方式,r…...

速盾:海外服务器用了cdn还是卡怎么办
海外服务器使用CDN卡顿问题的解决办法 在如今互联网高速发展的时代,海外服务器成为了许多企业和个人用户的首选,因为它能够提供更高的带宽和更稳定的网络连接。然而,尽管海外服务器在网络性能方面表现出色,但在使用过程中仍然可能…...

[python-opencv] PNG 裁切物体
拿到一组图PNG的图,边缘有点太宽了,需要裁切一下,为了这个需求,简单复习一下基本语法。 1. 读取PNG的4个通道 image cv.imread(image_path, cv.IMREAD_UNCHANGED) 附参数说明: IMREAD_UNCHANGED -1 返…...
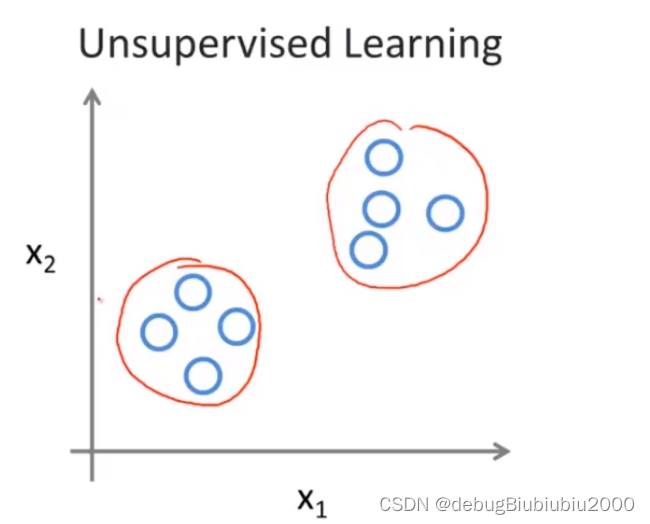
机器学习——有监督学习和无监督学习
有监督学习 简单来说,就是人教会计算机学会做一件事。 给算法一个数据集,其中数据集中包含了正确答案,根据这个数据集,可以对额外的数据希望得到一个正确判断(详见下面的例子) 回归问题 例如现在有一个…...

MySQL单主模式部署组复制集群
前言 本篇文章介绍MySQL8.0.27版本的组复制详细搭建过程,教你如何快速搭建一个三节点的单主模式组复制集群。 实际上,MySQL组复制是MySQL的一个插件 group_replication.so,组中的每个成员都需要配置并安装该插件,配置和安装过程…...

【大厂AI课学习笔记】【1.5 AI技术领域】(10)对话系统
对话系统,Dialogue System,也称为会话代理。是一种模拟人类与人交谈的计算机系统,旨在可以与人类形成连贯通顺的对话,通信方式主要有语音/文本/图片,当然也可以手势/触觉等其他方式 一般我们将对话系统,分…...

【ARM 嵌入式 编译系列 2.7 -- GCC 编译优化参数详细介绍】
请阅读【嵌入式开发学习必备专栏 】 文章目录 GCC 编译优化概述常用优化等级-O1 打开的优化选项-O2 打开的优化选项-O3 打开的优化选项-Os 打开的优化选项优化技术使用优化选项的注意事项GCC 编译优化概述 GCC(GNU Compiler Collection)包含了用于C、C++、Objective-C、Fort…...
《剑指 Offer》专项突破版 - 面试题 38、39 和 40 : 通过三道面试题详解单调栈(C++ 实现)
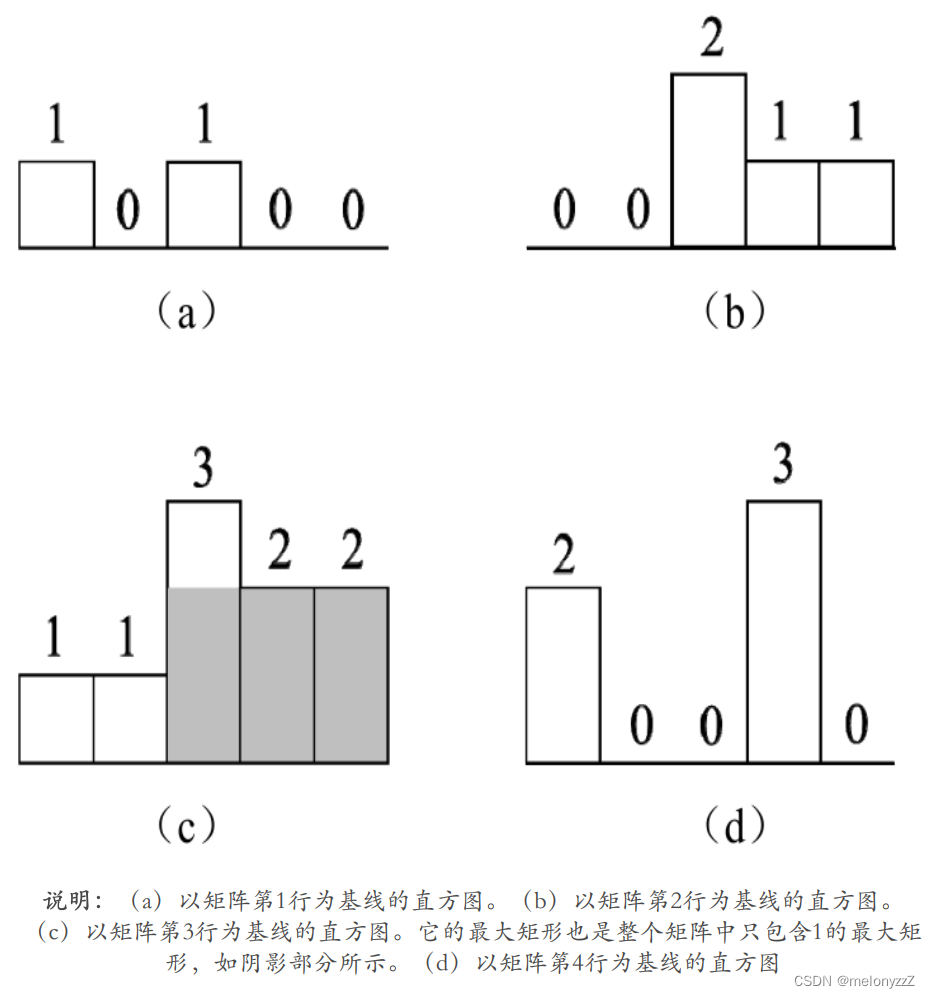
目录 面试题 38 : 每日温度 面试题 39 : 直方图最大矩形面积 方法一、暴力求解 方法二、递归求解 方法三、单调栈法 面试题 40 : 矩阵中的最大矩形 面试题 38 : 每日温度 题目: 输入一个数组,它的每个数字是某天的温度。请计算每天需要等几天才会…...

动态规划C语言
#include <stdio.h> #include <stdlib.h> //0-1背包问题是一种经典的组合优化问题, //问题描述为:有一个给定容量的背包和一组具有不同价值和重量的物品,如何选择物品放入背包中,以使得背包中物品的总价值最大化&…...
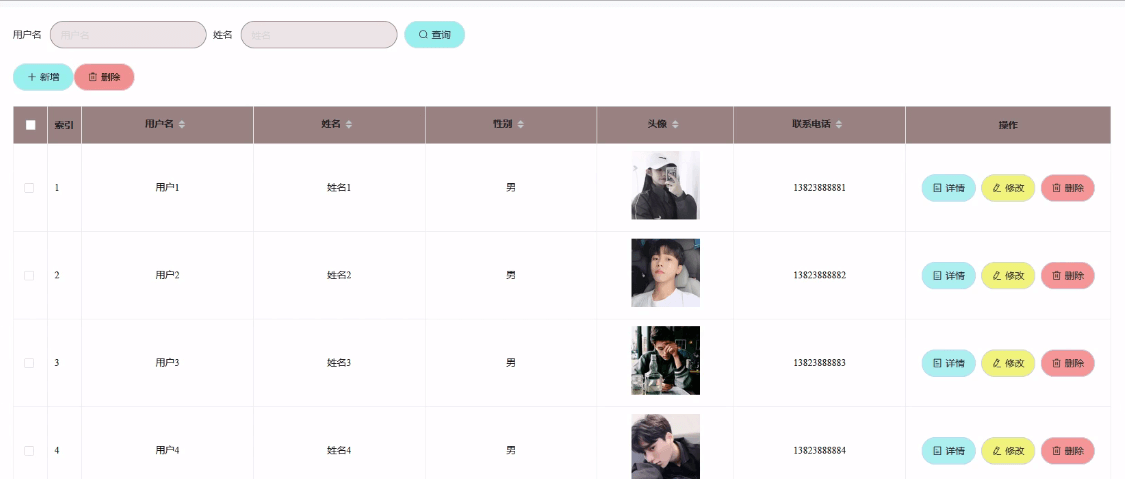
基于微信小程序的校园二手交易平台
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
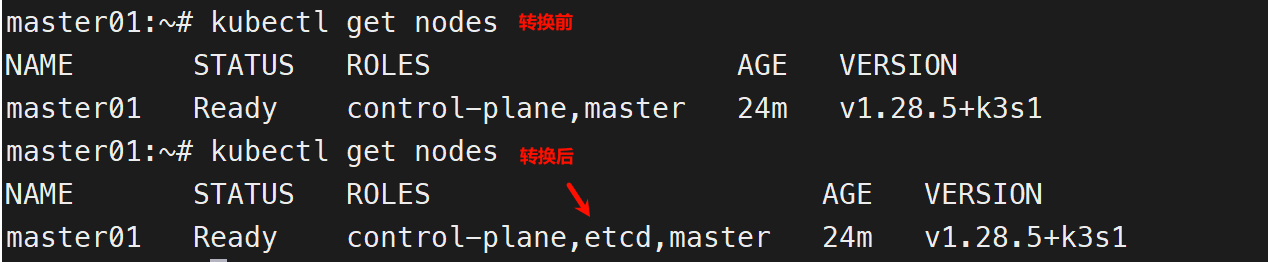
K8S系列文章之 [使用 Alpine 搭建 k3s]
官方文档:K3s - 轻量级 Kubernetes | K3s 官方描述,可运行在 systemd 或者 openrc 环境上,那就往精简方向走,使用 alpine 做系统。与 RHEL、Debian 的区别,主要在防火墙侧;其他基础配置需求类似࿰…...
计算机视觉 | OpenCV 实现手势虚拟控制亮度和音量
Hi,大家好,我是半亩花海。在当今科技飞速发展的时代,我们身边充斥着各种智能设备,然而,如何更便捷地与这些设备进行交互却是一个不断被探索的课题。本文将主要介绍一个基于 OpenCV 的手势识别项目,通过手势…...
python28-Python的运算符之三目运算符
Python可通过if语句来实现三目运算符的功能,因此可以近似地把这种if语句当成三目运算符。作为三目运算符的f语句的语法格式如下 True_statements if expression else False_statements 三目运算符的规则是:先对逻辑表达式expression求值,如果逻辑表达式…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
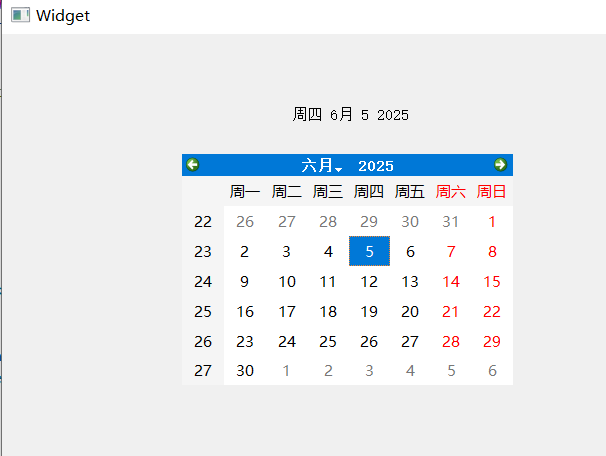
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
