可达鸭二月月赛——基础赛第六场(周五)题解,这次四个题的题解都在这一篇文章内,满满干货,含有位运算的详细用法介绍。
姓名
- 王胤皓
T1 题解
T1 题面

T1 思路
样例输入就是骗人的,其实直接输出就可以了,输出 Hello 2024,注意,中间有一个空格!
T1 代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){cout<<"Hello 2024";return 0;
}
T2 题解
T2题面

T2 思路
计算 2 x 2^x 2x 次方,可以使用 C++ 中自带的位运算。
接下来将详细介绍位运算:
位运算是计算机中一种常用的运算方式,它直接对二进制数据进行操作。C++语言提供了多种位运算操作符与函数,可以方便地进行位运算。
一、位运算的基础概念
- 二进制表示:在计算机中,所有的数据都是以二进制形式表示的。一个二进制位可以表示0或1,多个二进制位可以表示更大的数值。
- 位运算操作符:C++提供了多种位运算操作符,包括与(&)、或(|)、异或(^)、取反(~)等。
- 位运算函数:C++提供了一些位运算函数,包括位移函数(<<、>>)、位计数函数(__builtin_popcount)、最低位函数(__builtin_ffs)等。
二、位运算操作符
4. 与运算(&):对两个数的二进制位进行逐位比较,若两个位均为1,则结果为1;否则为0。例如,3 & 5的结果是1。
5. 或运算(|):对两个数的二进制位进行逐位比较,若两个位中至少有一个为1,则结果为1;否则为0。例如,3 | 5的结果是7。
6. 异或运算(^):对两个数的二进制位进行逐位比较,若两个位不相同,则结果为1;否则为0。例如,3 ^ 5的结果是6。
7. 取反运算(~):对一个数的二进制位进行逐位取反,即0变为1,1变为0。
例如,~3的结果是-4(以补码形式表示)。
8. 左移运算(<<):将一个数的二进制位向左移动指定的位数,相当于乘以2的指定次幂。例如,3 << 2的结果是12。
9. 右移运算(>>):将一个数的二进制位向右移动指定的位数,相当于除以2的指定次幂。例如,8 >> 2的结果是2。
三、位运算的应用
11. 位运算与(&)常用于掩码操作、判断奇偶性等。例如,可以用掩码操作实现只保留某些位。
12. 位运算或(|)常用于设置某些位为1。例如,可以用位运算将某些位设置为1,而保持其他位不变。
13. 位运算异或(^)常用于交换两个数的值、判断两个数的符号是否相同等。
14. 位运算取反(~)常用于将整数取反。
15. 位运算左移(<<)和右移(>>)常用于对整数进行乘法或除法的优化。例如,一个数左移一位相当于乘以2,右移一位相当于除以2。
四、位运算的特点
16. 位运算是直接对二进制数据进行操作,因此速度较快。
17. 位运算在一些特定场景下可以实现高效的算法,如位图算法、哈希表实现等。
18. 位运算可以用于优化算法性能,减少空间占用。
五、注意事项
19. 在使用位运算时,需要注意位运算的优先级与结合性,可以使用括号来明确运算顺序。
总结:位运算是C++中一种常用的运算方式,可用于对二进制数据进行操作。C++提供了多种位运算操作符和函数,方便进行位运算。位运算具有速度快、可以实现高效算法、可以优化性能的特点。在使用位运算时,需要注意操作符优先级和结合性。
所以直接输出 2 n 2^n 2n 也就是 1 < < n 1<<n 1<<n。
(我绝不会告诉你有人还用快速幂、pow和for循环)
T2 代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){int n;cin>>n;cout<<(1<<n);return 0;
}
T3 题解
T3 题面

T3 O ( n ) O(n) O(n) 思路
暴力枚举。
遍历 l l l 到 r r r,然后如果 i i i 为奇数,那么计数器加上 i i i,最后进行输出即可。
T3 O ( n ) O(n) O(n) 代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){int l,r;cin>>l>>r;int sum=0;for(int i=l;i<=r; i++){if(i&1) sum+=i;}cout<<sum;return 0;
}
T3 O(1) 思路
前置知识(干货):因为 1 + 3 + 5 + 7 + 9 = ⌊ 9 + 1 2 ⌋ 2 1+3+5+7+9=\lfloor \frac{9+1}{2}\rfloor^2 1+3+5+7+9=⌊29+1⌋2,从而得出 1 + 3 + 5 + ⋯ + n ( n m o d 2 = 1 ) = ⌊ n + 1 2 ⌋ 2 1+3+5+\cdots+n(n\mod 2=1)=\lfloor \frac{n+1}{2}\rfloor^2 1+3+5+⋯+n(nmod2=1)=⌊2n+1⌋2。
接下来进行分类讨论:
- 如果 l l l 和 r r r 都是奇数,那么根据约分性质 ( a + b + c + d ) − ( a + b ) = c + d (a+b+c+d)-(a+b)=c+d (a+b+c+d)−(a+b)=c+d,就能得出 1 + 3 + 5 + ⋯ + r 1+3+5+\cdots +r 1+3+5+⋯+r 和 1 + 3 + 5 + ⋯ + ( l − 2 ) 1+3+5+\cdots +(l-2) 1+3+5+⋯+(l−2),得出答案是 1 + 3 + 5 + ⋯ + r − ( 1 + 3 + 5 + ⋯ + ( l − 2 ) ) 1+3+5+\cdots +r-(1+3+5+\cdots +(l-2)) 1+3+5+⋯+r−(1+3+5+⋯+(l−2)),简化后为 r + 1 2 2 − l − 2 + 1 2 2 \frac{r+1}{2}^2-\frac{l-2+1}{2}^2 2r+12−2l−2+12。
Q:为什么 l l l 要减 2 2 2?
A:如果不减的话,那么就会少算一个 l l l。 - 如果 l l l 是奇数, r r r 是偶数,那么要把 r r r 减 1 1 1,然后就可以和 l l l 和 r r r 都是奇数的计算就是一样的了,就能得出 1 + 3 + 5 + ⋯ + r 1+3+5+\cdots +r 1+3+5+⋯+r 和 1 + 3 + 5 + ⋯ + ( l − 2 ) 1+3+5+\cdots +(l-2) 1+3+5+⋯+(l−2),得出答案是 1 + 3 + 5 + ⋯ + r − ( 1 + 3 + 5 + ⋯ + ( l − 2 ) ) 1+3+5+\cdots +r-(1+3+5+\cdots +(l-2)) 1+3+5+⋯+r−(1+3+5+⋯+(l−2)),简化后为 r + 1 2 2 − l − 2 + 1 2 2 \frac{r+1}{2}^2-\frac{l-2+1}{2}^2 2r+12−2l−2+12。
Q:为什么 l l l 要减 2 2 2?
A:如果不减的话,那么就会少算一个 l l l。 - 如果 l l l 是偶数, r r r 都是奇数,把 l + 1 l+1 l+1 ,然后就可以和 l l l 和 r r r 都是奇数的计算就是一样的了,那么根据约分性质 ( a + b + c + d ) − ( a + b ) = c + d (a+b+c+d)-(a+b)=c+d (a+b+c+d)−(a+b)=c+d,就能得出 1 + 3 + 5 + ⋯ + r 1+3+5+\cdots +r 1+3+5+⋯+r 和 1 + 3 + 5 + ⋯ + ( l − 2 ) 1+3+5+\cdots +(l-2) 1+3+5+⋯+(l−2),得出答案是 1 + 3 + 5 + ⋯ + r − ( 1 + 3 + 5 + ⋯ + ( l − 2 ) ) 1+3+5+\cdots +r-(1+3+5+\cdots +(l-2)) 1+3+5+⋯+r−(1+3+5+⋯+(l−2)),简化后为 r + 1 2 2 − l − 2 + 1 2 2 \frac{r+1}{2}^2-\frac{l-2+1}{2}^2 2r+12−2l−2+12。
Q:为什么 l l l 要减 2 2 2?
A:如果不减的话,那么就会少算一个 l l l。 - 如果 l l l 和 r r r 都是偶数,那么结合第二项和第三项,在进行第一项的操作就可以了,就是 l + 1 , r − 1 l+1,r-1 l+1,r−1,那么根据约分性质 ( a + b + c + d ) − ( a + b ) = c + d (a+b+c+d)-(a+b)=c+d (a+b+c+d)−(a+b)=c+d,就能得出 1 + 3 + 5 + ⋯ + r 1+3+5+\cdots +r 1+3+5+⋯+r 和 1 + 3 + 5 + ⋯ + ( l − 2 ) 1+3+5+\cdots +(l-2) 1+3+5+⋯+(l−2),得出答案是 1 + 3 + 5 + ⋯ + r − ( 1 + 3 + 5 + ⋯ + ( l − 2 ) ) 1+3+5+\cdots +r-(1+3+5+\cdots +(l-2)) 1+3+5+⋯+r−(1+3+5+⋯+(l−2)),简化后为 r + 1 2 2 − l − 2 + 1 2 2 \frac{r+1}{2}^2-\frac{l-2+1}{2}^2 2r+12−2l−2+12。
Q:为什么 l l l 要减 2 2 2?
A:如果不减的话,那么就会少算一个 l l l。
T3 O(1) 代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){int l,r;cin>>l>>r;if(r&1==0) r--;l--;if(l&1==0) l--;cout<<(((r+1)/2)*((r+1)/2)-((l+1)/2)*((l+1)/2))<<endl;return 0;
}
T4 题解
T4 题面

T4 思路
遍历字符串,如果 s i s_i si 和 s i + 1 s_{i+1} si+1 都是 l,那么计数器 + 1 +1 +1,然后把 i i i 也加 1 1 1,防止重复计算。
判断 s i = = ′ d ′ s_i=='d' si==′d′ 并且 s i + 1 = = ′ r ′ s_{i+1}=='r' si+1==′r′ 并且 s i + 2 = = ′ a ′ s_{i+2}=='a' si+2==′a′ 并且 s i + 3 = = ′ g ′ s_{i+3}=='g' si+3==′g′ 并且 s i + 4 = = ′ o ′ s_{i+4}=='o' si+4==′o′ 并且 s i + 5 = = ′ n ′ s_{i+5}=='n' si+5==′n′,可以使用 string 中的 substr 函数简化,函数格式:字符串名字.substr(截取字符串开始下标,截取长度),直接判断是否为 d r a g o n dragon dragon 就可以了。那么计数器也 + 1 +1 +1,然后 i + 5 i+5 i+5,防止重复计算。
T4 代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){int n;cin>>n;while(n--){string s;cin>>s;int cnt=0;for(int i=0; i<s.size()-1; i++){if(s[i]=='l'&&s[i+1]=='l'){i++;cnt+=2;}if(s.substr(i,6)=="dragon") cnt++,i+=5;}cout<<cnt<<endl;}return 0;
}
赛后总结
T1,T2,T3,T4真的都太水了,太简单了,前三题时间复杂度都可以做到 O ( 1 ) O(1) O(1),第四题最坏情况下是 O ( T × n ) O(T\times n) O(T×n)。
贴图:

给个三连,你的三连是给我创作文章的最大的动力!
相关文章:

可达鸭二月月赛——基础赛第六场(周五)题解,这次四个题的题解都在这一篇文章内,满满干货,含有位运算的详细用法介绍。
姓名 王胤皓 T1 题解 T1 题面 T1 思路 样例输入就是骗人的,其实直接输出就可以了,输出 Hello 2024,注意,中间有一个空格! T1 代码 #include<bits/stdc.h> using namespace std; #define ll long long int …...
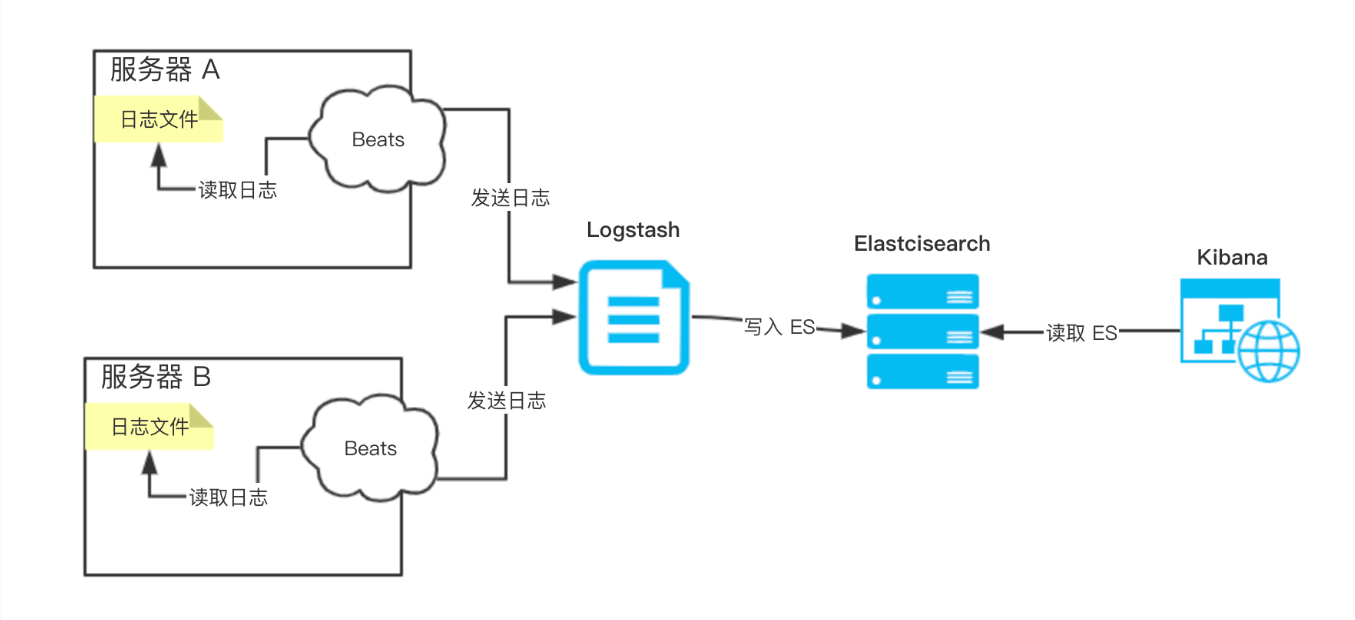
ELFK日志采 - QuickStart
文章目录 架构选型ELKEFLK ElasticsearchES集群搭建常用命令 Filebeat功能介绍安装步骤Filebeat配置详解filebeat常用命令 Logstash功能介绍安装步骤Input插件Filter插件Grok Filter 插件Mutate Filter 插件常见的插件配置选项:Mutate Filter配置案例: O…...
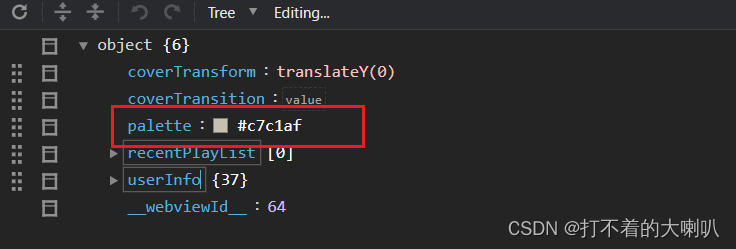
微信小程序的图片色彩分析,窃取网络图片的主色调
1、安装 Mini App Color Thief 包 包括下载包,简单使用都有,之前写了,这里就不写了 网址:微信小程序的图片色彩分析,窃取主色调,调色板-CSDN博客 2、 问题和解决方案 问题:由于我们的窃取图片的…...

Leetcode 121 买卖股票的最佳时机
题意理解: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交…...

SQL语言复习-----1
1,前言 SQL是计算机的一门基础语言,无论在开发还是数据库管理上都是非常重要,最近总结归纳了一下相关知识,记录如下。 2,归纳 SQL是结构化查询语言。 关系数据库有三级模式结构。 基本表和视图一样都是关系。 举例…...
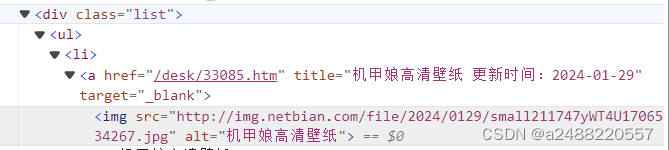
爬虫2—用爬虫爬取壁纸(想爬多少张爬多少张)
先看效果图: 我这个是爬了三页的壁纸60张。 上代码了。 import requests import re import os from bs4 import BeautifulSoupcount0 img_path "./壁纸图片/"#指定保存地址 if not os.path.exists(img_path):os.mkdir(img_path) headers{ "User-Ag…...

学习Android的第九天
目录 Android Button 按钮 基本的按钮 StateListDrawable 范例 使用颜色值绘制圆角按钮 自制水波纹效果 Android ImageButton 图片按钮 ImageButton 不同状态下的 ImageButton Android RadioButton 单选按钮 RadioButton 获得选中的值 Android Button 按钮 在 And…...

课时21:内置变量_脚本相关
2.4.1 脚本相关 学习目标 这一节,我们从 基础知识、简单实践、小结 三个方面来学习 基础知识 脚本相关的变量解析 序号变量名解析1$0获取当前执行的shell脚本文件名2$n获取当前执行的shell脚本的第n个参数值,n1…9,当n为0时表示脚本的文…...

ubuntu22.04@laptop OpenCV Get Started: 006_annotating_images
ubuntu22.04laptop OpenCV Get Started: 006_annotating_images 1. 源由2. line/circle/rectangle/ellipse/text 应用Demo3 image_annotation3.1 C应用Demo3.2 Python应用Demo3.3 重点过程分析3.3.1 划线3.3.2 画圆3.3.3 矩形3.3.4 椭圆3.3.5 文字 4. 总结5. 参考资料 1. 源由 …...

【制作100个unity游戏之23】实现类似七日杀、森林一样的生存游戏10(附项目源码)
本节最终效果演示 文章目录 本节最终效果演示系列目录前言快捷栏绘制UI代码控制快捷列表信息 源码完结 系列目录 前言 欢迎来到【制作100个Unity游戏】系列!本系列将引导您一步步学习如何使用Unity开发各种类型的游戏。在这第23篇中,我们将探索如何制作…...
uniapp vue3怎么调用uni-popup组件的this.$refs.message.open() ?
vue2代码 <!-- 提示信息弹窗 --><uni-popup ref"message" type"message"><uni-popup-message :type"msgType" :message"messageText" :duration"2000"></uni-popup-message></uni-popup>typ…...

【深度学习:语义分割】语义分割简介
【深度学习:语义分割】语义分割简介 什么是图像分割?了解语义分割数据采集语义分割的深度学习实现全卷积网络上采样跳跃连接U-NetDeepLab多尺度物体检测金字塔场景解析网络(PSPNet) 语义分割的应用医学影像自动驾驶汽车农业图片处…...

前端开发_AJAX基本使用
AJAX概念 AJAX是异步的JavaScript和XML(Asynchronous JavaScript And XML)。 简单点说,就是使用XMLHttpRequest对象与服务器通信。 它可以使用JSON,XML,HTML和text文本等格式发送和接收数据。 AJAX最吸引人的就是它的“异步"特性&am…...
OnlyOffice-8.0版本深度测评
OnlyOffice 是一套全面的开源办公协作软件,不断演进的 OnlyOffice 8.0 版本为用户带来了一系列引人瞩目的新特性和功能改进。OnlyOffice 8.0 版本在功能丰富性、安全性和用户友好性上都有显著提升,为用户提供了更为强大、便捷和安全的文档处理和协作环境…...

【Go】一、Go语言基本语法与常用方法容器
GO基础 Go语言是由Google于2006年开源的静态语言 1972:(C语言) — 1983(C)—1991(python)—1995(java、PHP、js)—2005(amd双核技术 web端新技术飞速发展&…...

杨中科 ASP.NETCORE 高级14 SignalR
1、什么是websocket、SignalR 服务器向客户端发送数据 1、需求:Web聊天;站内沟通。 2、传统HTTP:只能客户端主动发送请求 3、传统方案:长轮询(Long Polling)。缺点是?(1.客户端发送请求后&…...

哪家洗地机比较好用?性能好的洗地机推荐
在众多功能中,我坚信洗地机的核心依旧是卓越的清洁能力以及易于维护的便捷性,其他的附加功能可以看作是锦上添花,那么如何找到性能好的洗地机呢?我们一起看看哪些洗地机既能确保卫生效果还能使用便利。 洗地机工作原理࿱…...

学习与非学习
学习与非学习是人类和动物行为表现中的两种基本形式,它们在认知过程和行为适应上有着根本的区别。理解这两者之间的差异对于把握认知发展、心理学以及教育学等领域的核心概念至关重要。 学习 学习是一个获取新知识、技能、态度或价值观的过程,它导致行为…...
牛客网SQL进阶127: 月总刷题数和日均刷题数
官网链接: 月总刷题数和日均刷题数_牛客题霸_牛客网现有一张题目练习记录表practice_record,示例内容如下:。题目来自【牛客题霸】https://www.nowcoder.com/practice/f6b4770f453d4163acc419e3d19e6746?tpId240 0 问题描述 基于练习记录表…...

19:Web开发模式与MVC设计模式-Java Web
目录 19.1 Java Web开发模式19.2 MVC设计模式详解19.3 MVC与其他Java Web开发模式的区别总结19.4 应用场景总结 在Java Web应用程序开发领域,有效的架构模式和设计模式对提高代码可维护性、模块化以及团队协作至关重要。本文将探讨Java Web开发中的常见模式——模型…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
