InternLM大模型实战-4.XTuner大模型低成本微调实战
文章目录
- 前言
- 笔记正文
- XTuner
- 支持模型和数据集
- 微调原理
- 跟随文档学习
- 快速上手
- 自定义微调
- 准备数据
- 准备配置文件
- MS-Agent微调
前言
本文是对于InternLM全链路开源体系系列课程的学习笔记。【XTuner 大模型单卡低成本微调实战】 https://www.bilibili.com/video/BV1yK4y1B75J/?share_source=copy_web&vd_source=99d9a9488d6d14ace3c7925a3e19793e
笔记正文
XTuner
地址:XTuner
一个大预言模型微调工具箱
- 傻瓜化:以配置文件的形式封装了大部分微调场景
- 轻量级:对于7B参数量的LLM,微调所需的最小显存仅为8GB。
支持模型和数据集

微调原理
- LoRA:只对玩具中某些零件记性改动,而不是对整个玩具进行全面改动
- QLoRA:LoRA的一种改进,如果你手里只有一把生锈的螺丝刀,也能改造你的玩具。
跟随文档学习
文档提供了三个微调的例子,分别叫做快速上手、自定义微调和MS-Agent微调。
快速上手
首先介绍了如何安装微调的XTuner环境,然后介绍了具有多个开箱即用的配置文件,并对于这些配置文件的名称进行了解释
例如文件名:internlm_chat_7b_qlora_oasst1_e3
| 模型名 | internlm_chat_7b |
|---|---|
| 使用算法 | qlora |
| 数据集 | oasst1 |
| 把数据集跑几次 | 跑三次:e3 |
然后根据实际模型、数据集存放的位置、实际训练需求,修改配置文件中的信息。
接着就可以开始微调了。
微调训练完成后,应该在work_dirs的目录下产生pth权重,需要将其转换成hf格式的模型
xtuner convert pth_to_hf ${CONFIG_NAME_OR_PATH} ${PTH_file_dir} ${SAVE_PATH}
转换后,生成的文件应该是
|-- README.md
|-- adapter_config.json
|-- adapter_model.bin
`-- xtuner_config.py
可以理解为LoRA模型文件=Adapter
然后将hf的adapter合并到原LLM,并与之对话,这些需求xtuner都提供了相应的命令行工具。
自定义微调
这个部分演示了在实际需求下如何准备数据、修改配置文件、进行微调。
准备数据
将表格(或者其他数据格式)数据转化成jsonL格式。也就是json列表
[{"conversation":[{"system": "xxx","input": "xxx","output": "xxx"}]
},
{"conversation":[{"system": "xxx","input": "xxx","output": "xxx"}]
}]
然后划分训练集和测试集等。
准备配置文件
可以从下面的对配置文件的修改看出如何使用这种所谓的“自定义数据集”进行微调训练。
# 修改import部分
- from xtuner.dataset.map_fns import oasst1_map_fn, template_map_fn_factory
+ from xtuner.dataset.map_fns import template_map_fn_factory# 修改模型为本地路径
- pretrained_model_name_or_path = 'internlm/internlm-chat-7b'
+ pretrained_model_name_or_path = './internlm-chat-7b'# 修改训练数据为 MedQA2019-structured-train.jsonl 路径
- data_path = 'timdettmers/openassistant-guanaco'
+ data_path = 'MedQA2019-structured-train.jsonl'# 修改 train_dataset 对象
train_dataset = dict(type=process_hf_dataset,
- dataset=dict(type=load_dataset, path=data_path),
+ dataset=dict(type=load_dataset, path='json', data_files=dict(train=data_path)),tokenizer=tokenizer,max_length=max_length,
- dataset_map_fn=alpaca_map_fn,
+ dataset_map_fn=None,template_map_fn=dict(type=template_map_fn_factory, template=prompt_template),remove_unused_columns=True,shuffle_before_pack=True,pack_to_max_length=pack_to_max_length)
然后和前文差不多。
MS-Agent微调
数据也是由jsonl格式的,但是与前面的input、output不同,现在的每个conversations则需要赋予不同的身份了。
- system: 表示给模型前置的人设输入,其中有告诉模型如何调用插件以及生成请求
- user: 表示用户的输入 prompt,分为两种,通用生成的prompt和调用插件需求的 prompt
- assistant: 为模型的回复。其中会包括插件调用代码和执行代码,调用代码是要 LLM 生成的,而执行代码是调用服务来生成结果的
而assistant则需要包含工具调用和返回,分别叫做思考阶段和执行阶段,这两个阶段是不输出的,具体格式如下

图片来源https://github.com/InternLM/tutorial/blob/main/xtuner/README.md
之后就是找到对应的训练配置文件,根据实际情况等进行修改即可。
相关文章:

InternLM大模型实战-4.XTuner大模型低成本微调实战
文章目录 前言笔记正文XTuner支持模型和数据集 微调原理跟随文档学习快速上手自定义微调准备数据准备配置文件 MS-Agent微调 前言 本文是对于InternLM全链路开源体系系列课程的学习笔记。【XTuner 大模型单卡低成本微调实战】 https://www.bilibili.com/video/BV1yK4y1B75J/?…...

【SpringBoot篇】解决Redis分布式锁的 误删问题 和 原子性问题
文章目录 🍔Redis的分布式锁🛸误删问题🎈解决方法🔎代码实现 🛸原子性问题🌹Lua脚本 ⭐利用Java代码调用Lua脚本改造分布式锁🔎代码实现 🍔Redis的分布式锁 Redis的分布式锁是通过利…...

蓝桥杯Web应用开发-CSS3 新特性【练习三:文本阴影】
文本阴影 text-shadow 属性 给文本内容添加阴影的效果。 文本阴影的语法格式如下: text-shadow: x-offset y-offset blur color;• x-offset 是沿 x 轴方向的偏移距离,允许负值,必须参数。 • y-offset 是沿 y 轴方向的偏移距离,…...

LRU缓存
有人从网络读数据,有人从磁盘读数据,机智的人懂得合理利用缓存加速数据的读取效率,提升程序的性能,搏得上司的赏识,赢得白富美的青睐,进一步走向人生巅峰~ LRU假说 LRU缓存(Least Recently Used…...
ncc匹配提速总结
我们ncc最原始的匹配方法是:学习模板w*h个像素都要带入ncc公式计算 第一种提速,学习模板是w*h,而我们支取其中的w/2*h/2,匹配窗口同理,计算量只有1/4。 另外一种因为ncc是线性匹配,我们在这上面也做了文章࿰…...

人力资源智能化管理项目(day06:员工管理)
学习源码可以看我的个人前端学习笔记 (github.com):qdxzw/humanResourceIntelligentManagementProject 页面结构 <template><div class"container"><div class"app-container"><div class"left"><el-input style&qu…...

Java实现数据可视化的智慧河南大屏 JAVA+Vue+SpringBoot+MySQL
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、系统展示四、核心代码4.1 数据模块 A4.2 数据模块 B4.3 数据模块 C4.4 数据模块 D4.5 数据模块 E 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpringBootMySQL的数据可视化的智慧河南大屏,包含了GDP、…...
)
【Flink】FlinkSQL的DataGen连接器(测试利器)
简介 我们在实际开发过程中可以使用FlinkSQL的DataGen连接器实现FlinkSQL的批或者流模拟数据生成,DataGen 连接器允许按数据生成规则进行读取,但注意:DataGen连接器不支持复杂类型: Array,Map,Row。 请用计算列构造这些类型 创建有界DataGen表 CREATE TABLE test ( a…...

5G NR 频率计算
5G中引入了频率栅格的概念,也就是小区中心频点和SSB的频域位置不能随意配置,必须满足一定规律,主要目的是为了UE能快速的搜索小区;其中三个最重要的概念是Channel raster 、synchronization raster和pointA。 1、Channel raster …...
关于物理机ping不通虚拟机问题
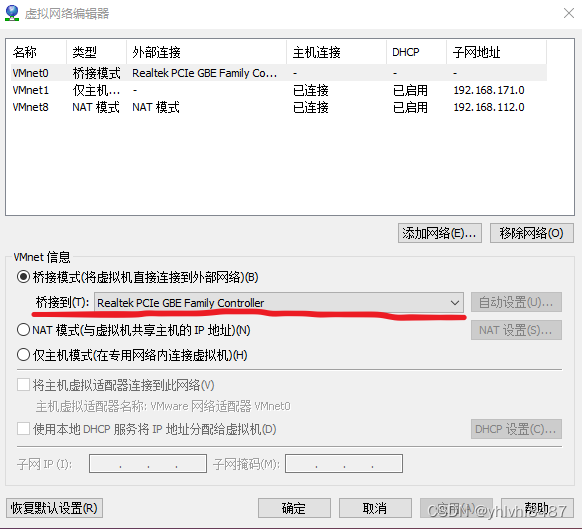
方法一 设置虚拟机处于桥接状态即可:(虚拟机->设置->网络适配器),选择完确定,重启虚拟机即可。 方法二 如果以上配置还是无法ping通:(编辑->虚拟网络编辑器) 首先查看主机网…...

深度学习在知识图谱问答中的革新与挑战
目录 前言1 背景知识2 基于深度学习改进问句解析模型2.1 谓词匹配2.2 问句解析2.3 逐步生成查询图 3 基于深度学习的端到端模型3.1 端到端框架3.2 简单嵌入技术 4 优势4.1 深入的问题表示4.2 实体关系表示深挖4.3 候选答案排序效果好 5 挑战5.1 依赖大量训练语料5.2 推理类问句…...
JAVA设计模式之职责链模式详解
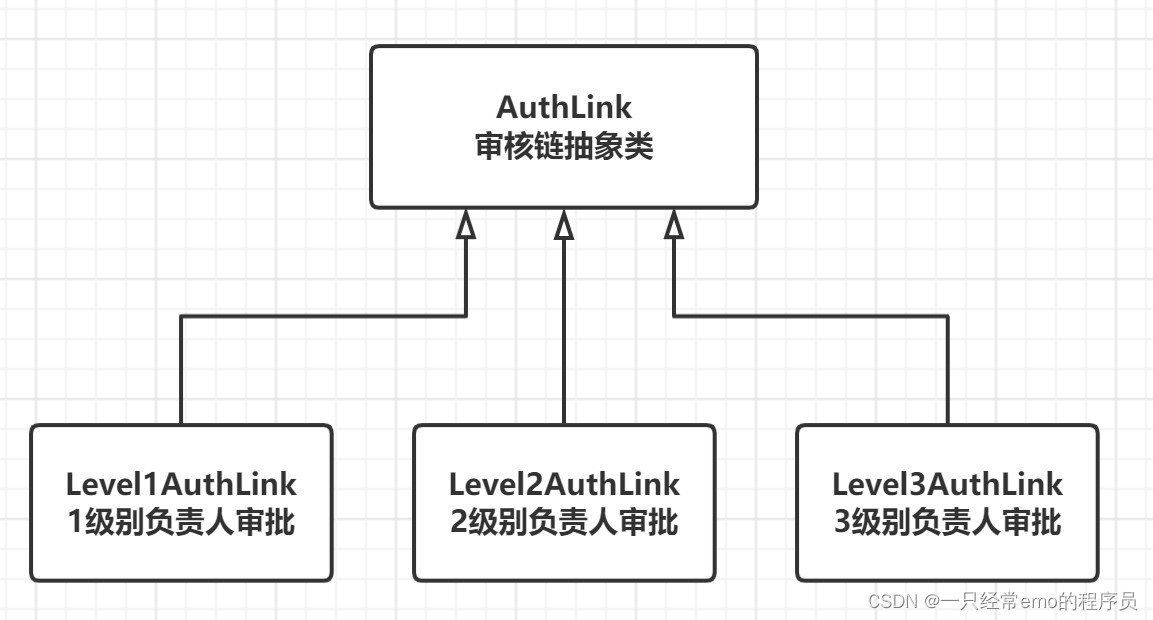
职责链模式 1 职责链模式介绍 职责链模式(chain of responsibility pattern) 定义: 避免将一个请求的发送者与接收者耦合在一起,让多个对象都有机会处理请求.将接收请求的对象连接成一条链,并且沿着这条链传递请求,直到有一个对象能够处理它为止. 在职责链模式中,…...

CSP-201912-1-报数
CSP-201912-1-报数 知识点总结 整数转化为字符串#include <string> string str_num to_string(num);字符串中查找是否包含字符‘7’:str_num.find(7) 未找到返回-1找到返回返回该字符在字符串中的位置(即第一次出现的索引位置) #i…...
前后端分离好处多多,怕就怕分工不分人,哈哈
前后端分离倡导多年了,现在基本成为了开发的主流模式了,贝格前端工场承接的前端项目只要不考虑seo的,都采用前后端分离模式,这篇文章就来介绍一下前后端分离模式。 一、什么是前后端分离开发模式 前后端分离是一种软件开发的架构…...
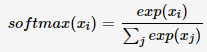
机器学习:Softmax介绍及代码实现
Softmax原理 Softmax函数用于将分类结果归一化,形成一个概率分布。作用类似于二分类中的Sigmoid函数。 对于一个k维向量z,我们想把这个结果转换为一个k个类别的概率分布p(z)。softmax可以用于实现上述结果,具体计算公式为: 对于…...
python基于flask的网上订餐系统769b9-django+vue
课题主要分为两大模块:即管理员模块和用户模块,主要功能包括个人中心、用户管理、菜品类型管理、菜品信息管理、留言反馈、在线交流、系统管理、订单管理等; 如果用户想要交换信息,他们需要满足双方交换信息的需要。由于时间有限…...
jenkins 发布远程服务器并部署项目
安装参考另一个文章 配置maven 和 jdk 和 git 注意jdk的安装目录,是jenkins 安装所在服务器的jdk目录 注意maven的目录 是jenkins 安装所在服务器的maven目录 注意git的目录 是jenkins 安装所在服务器的 git 目录 安装 Publish Over SSH 插件 配置远程服务器 创…...

【数学建模】【2024年】【第40届】【MCM/ICM】【D题 五大湖的水位控制问题】【解题思路】
一、题目 (一) 赛题原文 2024 ICM Problem D: Great Lakes Water Problem Background The Great Lakes of the United States and Canada are the largest group of freshwater lakes in the world. The five lakes and connecting waterways const…...

【开源】JAVA+Vue+SpringBoot实现公司货物订单管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 客户管理模块2.2 商品维护模块2.3 供应商管理模块2.4 订单管理模块 三、系统展示四、核心代码4.1 查询供应商信息4.2 新增商品信息4.3 查询客户信息4.4 新增订单信息4.5 添加跟进子订单 五、免责说明 一、摘要 1.1 项目…...

###C语言程序设计-----C语言学习(12)#进制间转换,十进制,二进制,八进制,十六进制
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 计算机处理的所有信息都以二进制形式表示,即数据的存储和计算都采…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
