【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线
目录
- 一、说明
- 二、贝塞尔曲线特征
- 三、模拟
- 四、全部代码如下
- 五、资源和下载
一、说明
以下文章介绍了用 C++ 计算和绘制的贝塞尔曲线(2D 和 3D)。
贝塞尔曲线具有出色的数学能力来计算路径(从起点到目的地点的曲线)。曲线的形状由“控制点”决定。所讨论的曲线最重要的特征是平滑度。
在许多应用和领域中,平滑度是不可或缺的。我们可以考虑机器人或其他机器的运动,其中运动必须是可预测的,以确保人员和硬件的安全(低磨损系数)。当机器人关节的轨迹被计算为平滑路径时,我们可以假设机器人将按照规划的路径平滑地移动,不会出现急动或意外移动。请注意,在我们考虑的机器人技术中,除了路径之外,还有速度、加速度、冲击力和电机扭矩。所有这些参数主要影响最终路径。
除了机器人技术之外,贝塞尔曲线还用于动画、游戏和设计。
为了绘图的目的,我将使用我之前的文章中讨论过的 C++ 的 matplotlib 库。
头文件(用于绘图库)必须与您的 cpp 位于同一文件夹中。您的程序可以按如下方式编译,
//compile
g++ my_prog.cpp -o my_prog -I/usr/include/python3.8 -lpython3.8//
//run
./my_prog
//folder tree
├── my_prog
├── my_prog.cpp
├── matplotlibcpp.h
二、贝塞尔曲线特征
可以计算点集的贝塞尔曲线: { P0, P1, P2 …Pn},其中n定义我们建模的曲线(多项式)的阶数。在每种情况下,第一个点和最后一个点定义曲线的起点和终点的位置。其他点 - 控制点通常不属于计算的曲线,而是影响贝塞尔曲线的形状。
2D中的每个点P都有两个{x,y}笛卡尔坐标,但在3D中,点P按预期由三个{x, y, z}定义。
贝塞尔曲线的显式定义可以指定如下(我们将在模拟中使用这个公式)。
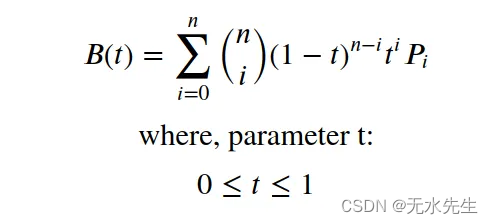
这里
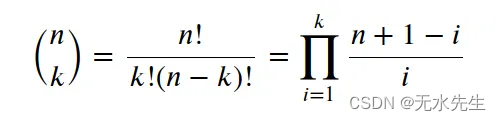
是二项式系数。
在我们的例子中,二项式系数的计算如下(如果您查看维基百科,您会发现递归实现,但这是最简单的版本或更直观)。
C++ 中的实现可以如下所示,
double computeBinominal(int n, int k)
{double value = 1.0;for (int i = 1; i <= k; i++){value = value * ((n + 1 - i) / i);}if (n == k){value = 1;}return value;
}
平面空间中的四个点P 0 、P 1 、P 2 和P 3 定义三次贝塞尔曲线。该曲线可以建模为三阶多项式。
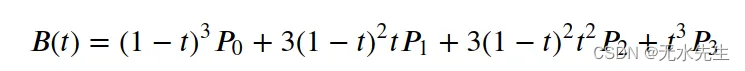
当提供六个点P 0、P 1、P 2、P 3、P4和P5时,贝塞尔曲线被计算为五阶多项式。
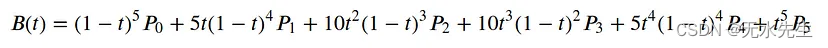
三、模拟
现在我们将显示上面定义的曲线的 2D 和 3D 模拟(针对 4 点和 6 点)。下面的代码为您提供了计算和绘制您想要的任何数字点P 的贝塞尔曲线的绝佳机会。
x{2.5, 1.5, 6.0, 10.0};
y{0.5, 5.0, 5.0, 0.5};x{2.5, 1.5, 6.0, 10.0};
//与 2D y{0.5, 5.0, 5.0, 0.5}相同;
//与 2D z{1.0, 2.0, 3.0, 4.0}相同;X{2.5, 1.5, 6, 10, 7, 3};
Y{0.5, 5.0, 5.0, 0.5, 1.0, 2.0};X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; // 对于 2D
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; // 对于 2D
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};
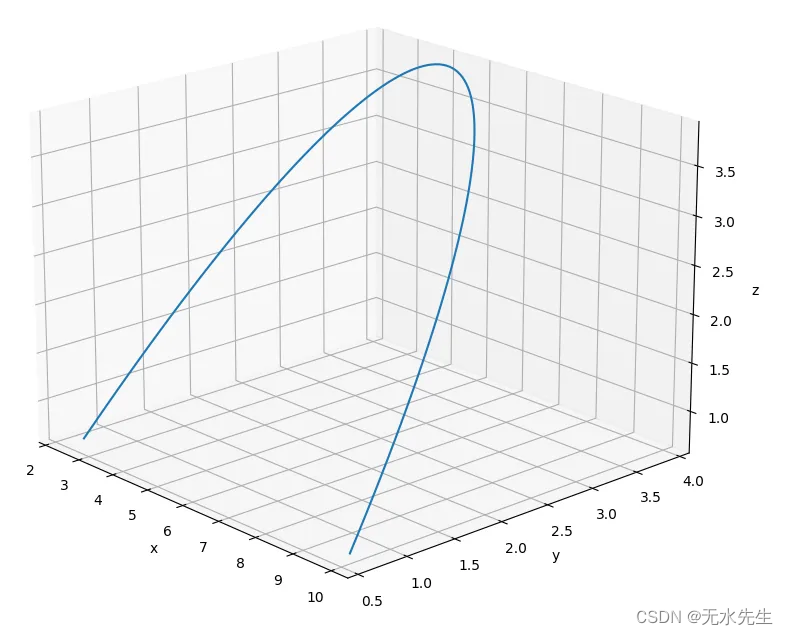
对于相同阶的多项式(三阶),我们可以计算 3D 贝塞尔曲线。
x{2.5, 1.5, 6.0, 10.0}; //same as 2D
y{0.5, 5.0, 5.0, 0.5}; //same as 2D
z{1.0, 2.0, 3.0, 4.0};
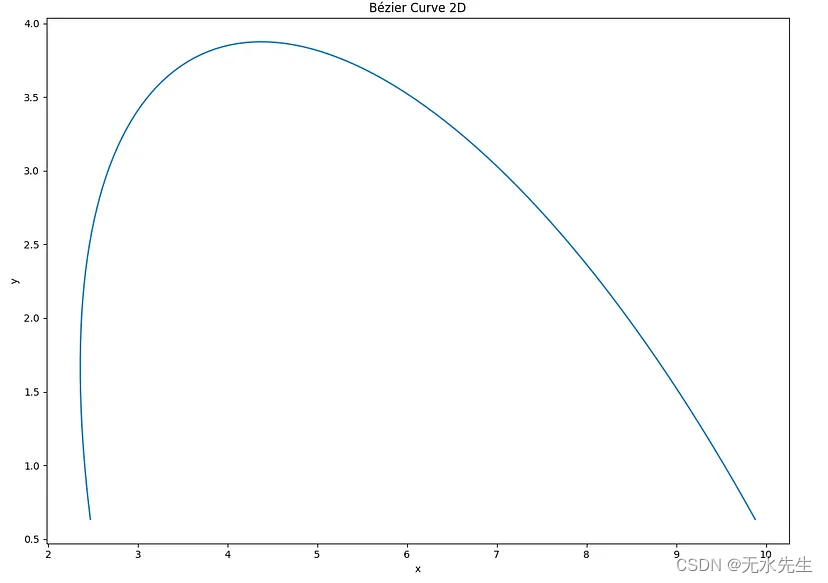
这是一条 2D 贝塞尔曲线,它是针对五阶多项式(六点)计算的。
X{2.5, 1.5, 6, 10, 7, 3};
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0};
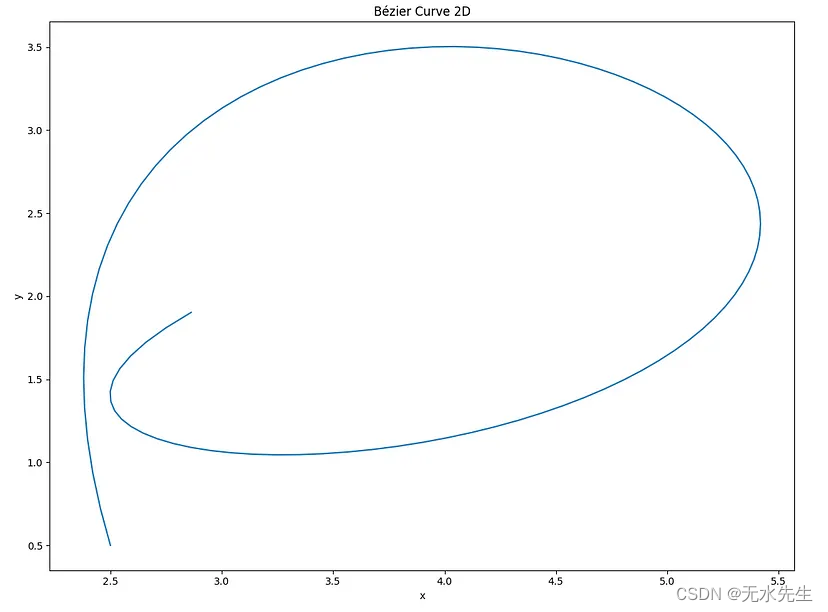
和以前一样,我们可以绘制 3D 贝塞尔曲线。
X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; //as for 2D
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; //as for 2D
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};
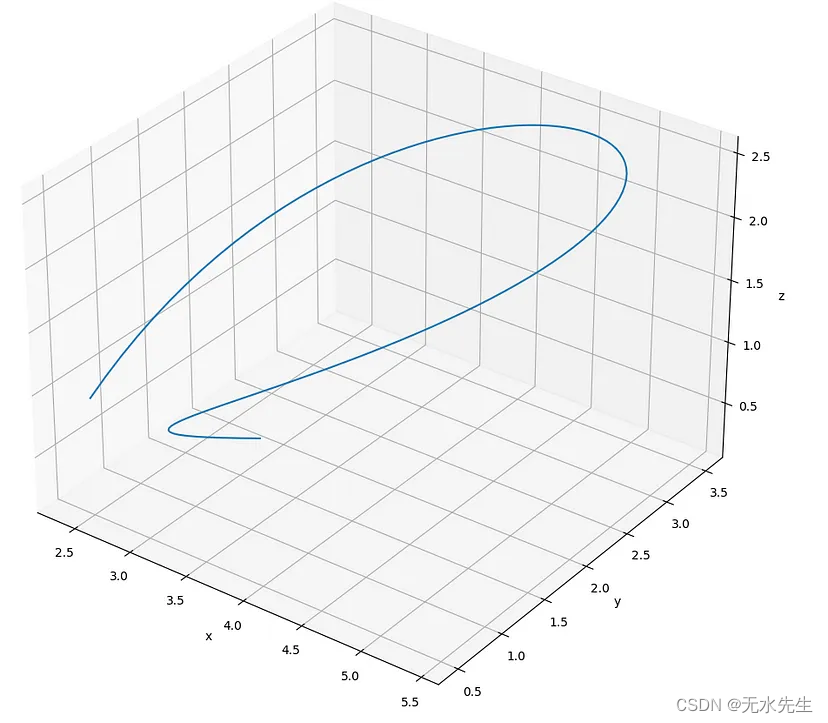
四、全部代码如下
/// g++ bezier_curve.cpp -o t -I/usr/include/python3.8 -lpython3.8#include <iostream>
#include <vector>
#include <tuple>
#include <math.h>#include "matplotlibcpp.h"namespace plt = matplotlibcpp;//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>> computeBesierCurve2D(std::vector<double> xX, std::vector<double> yY)
{std::vector<double> bCurveX;std::vector<double> bCurveY;double bCurveXt;double bCurveYt;for (double t = 0.01; t <= 1; t += 0.01){bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);}return std::make_tuple(bCurveX, bCurveY);
}//-----------------------------------------------------------void plot2D(std::tuple<std::vector<double>, std::vector<double>> data)
{std::vector<double> xX = std::get<0>(data);std::vector<double> yY = std::get<1>(data);plt::plot(xX, yY);plt::show();
}//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeBesierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{std::vector<double> bCurveX;std::vector<double> bCurveY;std::vector<double> bCurveZ;double bCurveXt;double bCurveYt;double bCurveZt;for (double t = 0.01; t <= 1; t += 0.01){bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveZt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);bCurveZ.push_back(bCurveZt);}return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}//-----------------------------------------------------------void plot3Dexample()
{std::vector<double> xX;std::vector<double> yY;std::vector<double> zZ;double theta;double r;double z_inc = 4.0 / 99.0;double theta_inc = (8.0 * M_PI) / 99.0;for (double i = 0; i < 100; i += 1){theta = -4.0 * M_PI + theta_inc * i;zZ.push_back(-2.0 + z_inc * i);r = zZ[i] * zZ[i] + 1;xX.push_back(r * std::sin(theta));yY.push_back(r * std::cos(theta));}plt::plot3(xX, yY, zZ);plt::show();
}//-----------------------------------------------------------void plot3D(std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> data)
{std::vector<double> xX = std::get<0>(data);std::vector<double> yY = std::get<1>(data);std::vector<double> zZ = std::get<2>(data);plt::plot3(xX, yY, zZ);plt::xlabel("x");plt::ylabel("y");plt::set_zlabel("z");plt::show();
}//-----------------------------------------------------------double computeBinominal(int n, int k)
{double value = 1.0;for (int i = 1; i <= k; i++){value = value * ((n + 1 - i) / i);}if (n == k){value = 1;}return value;
}//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>> computeNVertexBasierCurve2D(std::vector<double> xX, std::vector<double> yY)
{std::vector<double> bCurveX;std::vector<double> bCurveY;int n = xX.size() - 1;std::cout << "n :" << n << "\n";for (double t = 0.0; t <= 1.0; t += 0.01){double bCurveXt{0};double bCurveYt{0};for (int i = 0; i <= n; ++i){bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];//std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i) << " * " << std::pow((1 - t), (n - i)) << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;}bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);}return std::make_tuple(bCurveX, bCurveY);
}std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeNVertexBasierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{std::vector<double> bCurveX;std::vector<double> bCurveY;std::vector<double> bCurveZ;int n = xX.size() - 1;std::cout << "n :" << n << "\n";for (double t = 0.0; t <= 1.0; t += 0.01){double bCurveXt{0};double bCurveYt{0};double bCurveZt{0};for (int i = 0; i <= n; ++i){bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];bCurveZt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * zZ[i];//std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i) << " * " << std::pow((1 - t), (n - i)) << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;}bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);bCurveZ.push_back(bCurveZt);}return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}//-----------------------------------------------------------int main()
{std::vector<double> xX{2.5, 1.5, 6, 10};std::vector<double> yY{0.5, 5, 5, 0.5};std::vector<double> zZ{1.0, 2.0, 3.0, 4.0};std::tuple<std::vector<double>, std::vector<double>> bCurve2D = computeBesierCurve2D(xX, yY);plot2D(bCurve2D);std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3D = computeBesierCurve3D(xX, yY, zZ);plot3D(bCurve3D);std::vector<double> xXn{2.5, 1.5, 6, 10, 7, 3};std::vector<double> yYn{0.5, 5, 5, 0.5, 1.0 , 2.0};std::vector<double> zZn{1, 2, 3, 4, 5, 0.1};std::tuple<std::vector<double>, std::vector<double>> bCurve2DxN = computeNVertexBasierCurve2D(xXn, yYn);plot2D(bCurve2DxN);std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3DxN = computeNVertexBasierCurve3D(xXn, yYn, zZn);plot3D(bCurve3DxN);}
五、资源和下载
下面给出源代码资源下载链接地址:
https://download.csdn.net/download/gongdiwudu/88821722
相关文章:

【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线
目录 一、说明二、贝塞尔曲线特征三、模拟四、全部代码如下五、资源和下载 一、说明 以下文章介绍了用 C 计算和绘制的贝塞尔曲线(2D 和 3D)。 贝塞尔曲线具有出色的数学能力来计算路径(从起点到目的地点的曲线)。曲线的形…...
python+flask+django医院预约挂号病历分时段管理系统snsj0
技术栈 后端:python 前端:vue.jselementui 框架:django/flask Python版本:python3.7 数据库:mysql5.7 数据库工具:Navicat 开发软件:PyCharm . 第一,研究分析python技术,…...

《CSS 简易速速上手小册》第9章:CSS 最佳实践(2024 最新版)
文章目录 9.1 维护大型项目的 CSS9.1.1 基础知识9.1.2 重点案例:构建一个可复用的 UI 组件库9.1.3 拓展案例 1:优化现有项目的 CSS 结构9.1.4 拓展案例 2:实现主题切换功能 9.2 BEM、OOCSS 和 SMACSS 方法论9.2.1 基础知识9.2.2 重点案例&…...
Qt QVariant类应用
QVariant类 QVariant类本质为C联合(Union)数据类型,它可以保存很多Qt类型的值,包括 QBrush,QColor,QString等等,也能存放Qt的容器类型的值。 QVariant::StringList 是 Qt 定义的一个 QVariant::type 枚举类型的变量&…...

不到1s生成mesh! 高效文生3D框架AToM
论文题目: AToM: Amortized Text-to-Mesh using 2D Diffusion 论文链接: https://arxiv.org/abs/2402.00867 项目主页: AToM: Amortized Text-to-Mesh using 2D Diffusion 随着AIGC的爆火,生成式人工智能在3D领域也实现了非常显著…...

Mac中管理多版本Jdk
1. 首先下载JDK,以jdk8和17为例 2. 打开.zprofile中添加如下内容 #java config export JAVA_8_HOME/Library/Java/JavaVirtualMachines/zulu-8.jdk/Contents/Home export JAVA_17_HOME/Library/Java/JavaVirtualMachines/zulu-17.jdk/Contents/Home#default java …...
用C语言列出Linux或Unix上的网络适配器
上代码: 1. #include <sys/socket.h> 2. #include <stdio.h> 3. 4. #include <netdb.h> 5. #include <ifaddrs.h> 6. 7. int main() { 8. struct ifaddrs *addresses; 9. if(getifaddrs(&addresses) -1) { 10. printf("…...
单片机学习笔记---LED点阵屏显示图形动画
目录 LED点阵屏显示图形 LED点阵屏显示动画 最后补充 上一节我们讲了点阵屏的工作原理,这节开始代码演示! 前面我们已经说了74HC595模块也提供了8个LED,当我们不使用点阵屏的时候也可以单独使用74HC595,这8个LED可以用来测试7…...

Git分支常用指令
目录 1 git branch 2 git branch xx 3 git checkout xx 4 git checkout -b xx 5 git branch -d xx 6 git branch -D xx 7 git merge xx(含快进模式和冲突解决的讲解) 注意git-log: 1 git branch 作用:查看分支 示例: 2 git branch xx 作用&a…...

3.3 Binance_interface APP U本位合约行情-实时行情
Binance_interface APP U本位合约行情-实时行情 Github地址PyTed量化交易研究院 量化交易研究群(VX) py_ted目录 Binance_interface APP U本位合约行情-实时行情1. APP U本位合约行情-实时行情函数总览2. 模型实例化3. 获取一个产品的最优挂单 get_bookTicker4. 获取全部产品…...

机器学习——流形学习
流形学习是一种在机器学习领域中用于理解和分析数据的技术。它的核心思想是,尽管我们通常将数据表示为高维空间中的向量,但实际上数据可能具有较低维度的内在结构,这种结构被称为流形。流形学习的目标是发现并利用数据的这种潜在结构…...
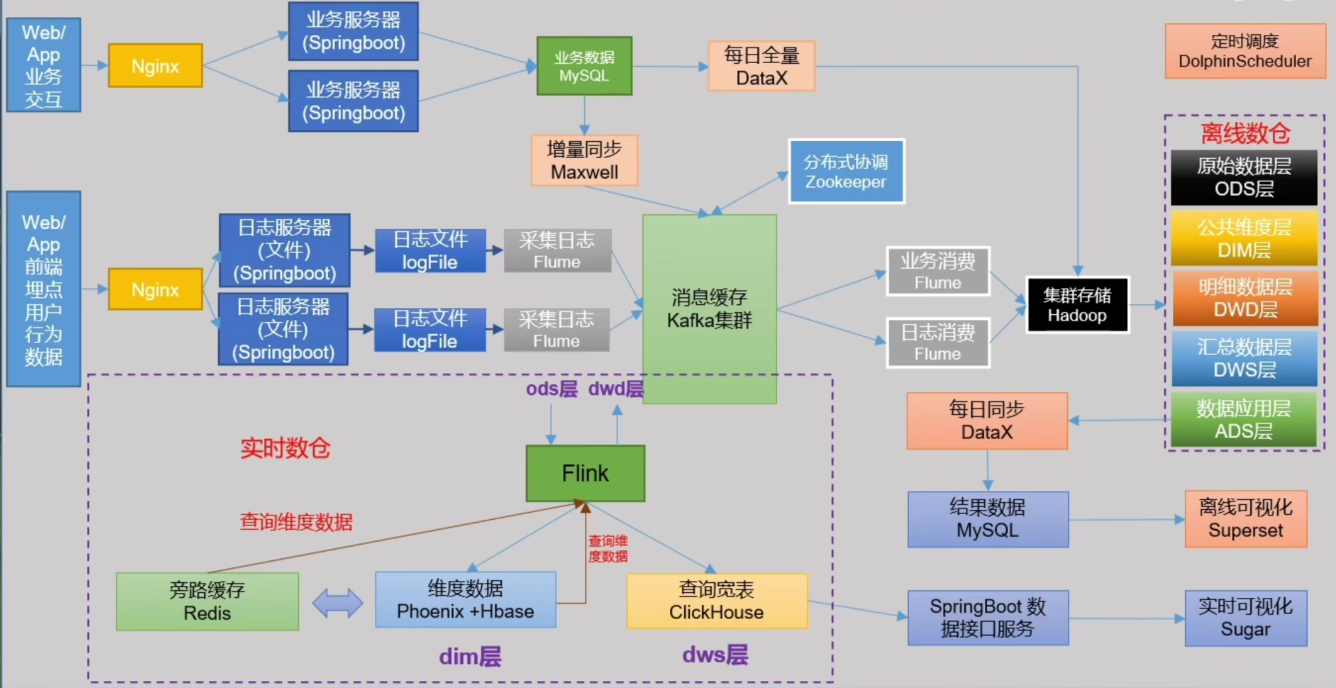
离线数仓(一)【数仓概念、需求架构】
前言 今天开始学习数仓的内容,之前花费一年半的时间已经学完了 Hadoop、Hive、Zookeeper、Spark、HBase、Flume、Sqoop、Kafka、Flink 等基础组件。把学过的内容用到实践这是最重要的,相信会有很大的收获。 1、数据仓库概念 1.1、概念 数据仓库&#x…...

物联网测试:2024 年的最佳实践和挑战
据 Transforma Insights 称,到 2030 年,全球广泛使用的物联网 (IoT) 设备预计将增加近一倍,从 151 亿台增至 290 亿台。这些设备以及智能汽车、智能手机等广泛应用于各种官僚机构。 健康视频监视器、闹钟以及咖啡机和冰箱等最受欢迎的家用电器…...

蓝桥杯Web应用开发-CSS3 新特性
CSS3 新特性 专栏持续更新中 在前面我们已经学习了元素选择器、id 选择器和类选择器,我们可以通过标签名、id 名、类名给指定元素设置样式。 现在我们继续选择器之旅,学习 CSS3 中新增的三类选择器,分别是: • 属性选择器 • 子…...

MongoDB聚合:$unionWith
$unionWith聚合阶段执行两个集合的合并,将两个集合的管道结果合并到一个结果集传送到下一个阶段。合并后的结果文档的顺序是不确定的。 语法 { $unionWith: { coll: "<collection>", pipeline: [ <stage1>, ... ] } }要包含集合的所有文档不…...

人工智能三子棋-人机对弈-人人对弈,谁会是最终赢家?
✅作者简介:大家好我是原始豌豆,感谢支持。 🆔本文由 原始豌豆 原创 CSDN首发🐒 如需转载还请通知⚠ 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言项目实践…...
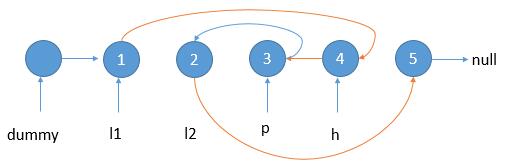
【leetcode热题100】反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

谷歌 DeepMind 联合斯坦福推出了主从式遥操作双臂机器人系统增强版ALOHA 2
谷歌 DeepMind 联合斯坦福推出了 ALOHA 的增强版本 ——ALOHA 2。与一代相比,ALOHA 2 具有更强的性能、人体工程学设计和稳健性,且成本还不到 20 万元人民币。并且,为了加速大规模双手操作的研究,ALOHA 2 相关的所有硬件设计全部开…...

金融行业专题|证券超融合架构转型与场景探索合集(2023版)
更新内容 更新 SmartX 超融合在证券行业的覆盖范围、部署规模与应用场景。新增操作系统信创转型、Nutanix 国产化替代、网络与安全等场景实践。更多超融合金融核心生产业务场景实践,欢迎阅读文末电子书。 在金融行业如火如荼的数字化转型大潮中,传统架…...

【C语言】C的整理记录
前言 该笔记是建立在已经系统学习过C语言的基础上,笔者对C语言的知识和注意事项进行整理记录,便于后期查阅,反复琢磨。C语言是一种面向过程的编程语言。 原想在此阐述一下C语言的作用,然而发觉这些是编程语言所共通的作用&#…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
