2.11学习总结
有效点对https://www.acwing.com/problem/content/description/5472/
给定一个 n� 个节点的无向树,节点编号 1∼n1∼�。
树上有两个不同的特殊点 x,y�,�,对于树中的每一个点对 (u,v)(u≠v)(�,�)(�≠�),如果从 u� 到 v� 的最短路径需要经过点 x� 和点 y�(路径的两个端点也算经过),且相对顺序上先经过点 x�,后经过点 y�,那么就称 (u,v)(�,�) 是一个无效点对,否则就称 (u,v)(�,�) 是一个有效点对。
请你计算树中有效点对的数量。
注意:
- (u,v)(�,�) 和 (v,u)(�,�) 是两个不同的点对。
- 有效点对必须满足 u≠v�≠�。
输入格式
第一行包含三个整数 n,x,y�,�,�。
接下来 n−1�−1 行,每行包含两个整数 a,b�,�,表示点 a� 和点 b� 之间存在一条无向边。
输出格式
一个整数,表示有效点对的数量。
数据范围
前 33 个测试点满足 1≤n≤101≤�≤10。
所有测试点满足 1≤n≤3×1051≤�≤3×105,1≤x,y≤n1≤�,�≤�,x≠y�≠�,1≤a,b≤n1≤�,�≤�,a≠b�≠�。
输入样例1:
3 1 3
1 2
2 3
输出样例1:
5
输入样例2:
3 1 3
1 2
1 3
输出样例2:
4思路:用DFS,只要计算出无效点,就可以得到有效点的数量,由于是树状结构,所以x点y的路径总和等于以x为根的子树大小*以y为根的子树大小
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int N=3e5+5;
int dp[N],vis[N];
vector<int>e[N];
void dfs(int u,int fa){dp[u]=1;for (int i=0;i<e[u].size();++i){int v=e[u][i];//if (vis[v]) continue;if (v!=fa){//vis[v]=1;dfs(v,u);dp[u]+=dp[v];//vis[v]=0;}}
}
signed main(){int n,x,y;cin>>n>>x>>y;for (int i=0;i<n-1;++i){int a,b;cin>>a>>b;e[a].push_back(b);e[b].push_back(a);}dfs(y,-1);int res=dp[x];for (int i=1;i<=n;++i) dp[i]=0;dfs(x,-1);res=dp[y]*res;res=n*(n-1)-res;cout<<res;
} 最有价值字符串https://www.acwing.com/problem/content/description/5471/
A,B,C�,�,� 三人在玩一个有关字符串的游戏。
给定三人每人一个由大小写字母构成的字符串。
三人的字符串的长度相同。
规定,一个字符串的价值等于该字符串中出现次数最多的子串的出现次数。
例如,aaaaaa 的价值为 66,因为出现次数最多的子串 a 一共出现了 66 次;abab 的价值为 22,因为出现次数最多的子串 ab 一共出现了 22 次。
游戏开始后,每人都需要对自己的字符串进行恰好 n� 次修改,每次修改需要将字符串中的某个字符修改为另一个不同的字符,例如将 aaab 修改为 acab。
所有修改完毕后,最有价值字符串的拥有者将获得游戏胜利。
请你计算,如果所有人都采取最优策略,那么谁将最终获胜。
输入格式
第一行包含整数 n�。
第二行,包含一个由大小写字母构成的字符串,表示给 A� 的字符串。
第三行,包含一个由大小写字母构成的字符串,表示给 B� 的字符串。
第四行,包含一个由大小写字母构成的字符串,表示给 C� 的字符串。
保证这三个人获得的字符串的长度均相同。
输出格式
共一行,A� 获胜则输出 A,B� 获胜则输出 B,C� 获胜则输出 C,不止一人获胜则输出 D。
数据范围
前 66 个测试点满足 0≤n≤200≤�≤20,每个输入字符串的长度范围 [1,20][1,20]。
所有测试点满足 0≤n≤1090≤�≤109,每个输入字符串的长度范围 [1,105][1,105]。
输入样例1:
3
abcdd
efgcd
hijgk
输出样例1:
A
输入样例2:
7
abcdefbcgfhi
igbccjbkchle
gkmnlcjnboce
输出样例2:
B
输入样例3:
1
abcabc
cbabac
ababca
输出样例3:
C
输入样例4:
15
abcdefghi
jkdlbmnop
jqrstduve
输出样例4:
D思路:先算出单个字符的最大价值,然后找到可更换的数量,和需要更换的次数,如果可更换的次数为0且需要更换次数为1,那么总数减1,否则,就是加上min(可更换次数,需要更换次数),如果可更换次数更大,那么所有需要更换次数都用在更换字符上,反之就是把可更换的字符都更换了
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
map<char,int>ma,mb,mc;
signed main(){int n;cin>>n;string a,b,c;cin>>a>>b>>c;int man=0,mbn=0,mcn=0;for (int i=0;i<a.size();++i){ma[a[i]]++;mb[b[i]]++;mc[c[i]]++;man=max(man,ma[a[i]]);mbn=max(mbn,mb[b[i]]);mcn=max(mcn,mc[c[i]]);}//找到可以交换的个数来提高价值int ka=0,kb=0,kc=0;ka=a.size()-man;kb=a.size()-mbn;kc=a.size()-mcn;//aaaaaaa ma=5 ka=0 n=3if (!ka && n==1) man=a.size()-1;else man+=min(ka,n);if (!kb && n==1) mbn=a.size()-1;else mbn+=min(kb,n);if (!kc&& n==1) mcn=a.size()-1;else mcn+=min(kc,n);if (man>mbn && man>mcn) cout<<"A";else if (mbn>man && mbn>mcn) cout<<"B";else if (mcn>man && mcn>mbn) cout<<"C";else cout<<"D";} 大臣的旅费https://www.luogu.com.cn/problem/P8602
题目描述
很久以前,T 王国空前繁荣。为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。
为节省经费,T 国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。
J 是 T 国重要大臣,他巡查于各大城市之间,体察民情。所以,从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。他有一个钱袋,用于存放往来城市间的路费。
聪明的 J 发现,如果不在某个城市停下来修整,在连续行进过程中,他所花的路费与他已走过的距离有关,在走第 �x 千米到第 �+1x+1 千米这一千米中(�x 是整数),他花费的路费是 �+10x+10 这么多。也就是说走 11 千米花费 1111,走 22 千米要花费 2323。
J 大臣想知道:他从某一个城市出发,中间不休息,到达另一个城市,所有可能花费的路费中最多是多少呢?
输入格式
输入的第一行包含一个整数 �(�≤105)n(n≤105),表示包括首都在内的 �T 王国的城市数。
城市从 11 开始依次编号,11 号城市为首都。
接下来 �−1n−1 行,描述 �T 国的高速路(�T 国的高速路一定是 �−1n−1 条)。
每行三个整数 ��,�,��Pi,Q,Di,表示城市 ��Pi 和城市 ��Qi 之间有一条高速路,长度为 ��(��≤1000)Di(Di≤1000) 米。
输出格式
输出一个整数,表示大臣J最多花费的路费是多少。
输入输出样例
输入 #1复制
5 1 2 2 1 3 1 2 4 5 2 5 4
输出 #1复制
135
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
int f[500005],vis[500005],dp[500005];
struct edge{int to;int w;edge(int a,int b){to=a;w=b;}
};
vector<edge>tree[500005];
void dfs(int u){vis[u]=1;for (int i=0;i<tree[u].size();++i){edge y=tree[u][i];if (vis[y.to])continue;dfs(y.to);f[u]=max(f[u],dp[u]+dp[y.to]+y.w);dp[u]=max(dp[u],dp[y.to]+y.w);}return ;
}
signed main(){int n; cin>>n;for (int i=0;i<n-1;++i){int u,v,w;cin>>u>>v>>w;tree[u].push_back(edge(v,w));tree[v].push_back(edge(u,w));}dfs(1);int res=f[1];for(int i=2;i<=n;++i){res=max(res,f[i]);} cout<<res*10+res*(res+1)/2;
}树的直径https://www.luogu.com.cn/problem/U81904
题目描述
给定一棵树,树中每条边都有一个权值,
树中两点之间的距离定义为连接两点的路径边权之和。
树中最远的两个节点之间的距离被称为树的直径,连接这两点的路径被称为树的最长链。
现在让你求出树的最长链的距离
输入格式
给定一棵无根树
第一行为一个正整数�n,表示这颗树有�n个节点
接下来的�−1n−1行,每行三个正整数�,�,�u,v,w,表示�,�u,v(�,�<=�u,v<=n)有一条权值为�w的边相连
数据保证没有重边或自环
输出格式
输入仅一行,表示树的最长链的距离
输入输出样例
输入 #1复制
6 1 2 1 1 3 2 2 4 3 4 5 1 3 6 2
输出 #1复制
9
说明/提示
对于1010的数据 �<=10n<=10
对于3030的数据 �<=1000n<=1000
对于5050的数据 �<=10000n<=10000
对于7070的数据 �<=100000n<=100000 边权均为正整数
对于100100的数据 �<=500000n<=500000 边权可能为负
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
int f[500005],vis[500005],dp[500005];
struct edge{int to;int w;edge(int a,int b){to=a;w=b;}
};
vector<edge>tree[500005];
void dfs(int u){vis[u]=1;for (int i=0;i<tree[u].size();++i){edge y=tree[u][i];if (vis[y.to])continue;dfs(y.to);f[u]=max(f[u],dp[u]+dp[y.to]+y.w);dp[u]=max(dp[u],dp[y.to]+y.w);}return ;
}
signed main(){int n; cin>>n;for (int i=0;i<n-1;++i){int u,v,w;cin>>u>>v>>w;tree[u].push_back(edge(v,w));tree[v].push_back(edge(u,w));}dfs(1);int res=f[1];for (int i=2;i<=n;++i){res=max(res,f[i]);}cout<<res;
}相关文章:

2.11学习总结
有效点对https://www.acwing.com/problem/content/description/5472/ 给定一个 n� 个节点的无向树,节点编号 1∼n1∼�。 树上有两个不同的特殊点 x,y�,�,对于树中的每一个点对 (u,v)(u≠v)(�,…...
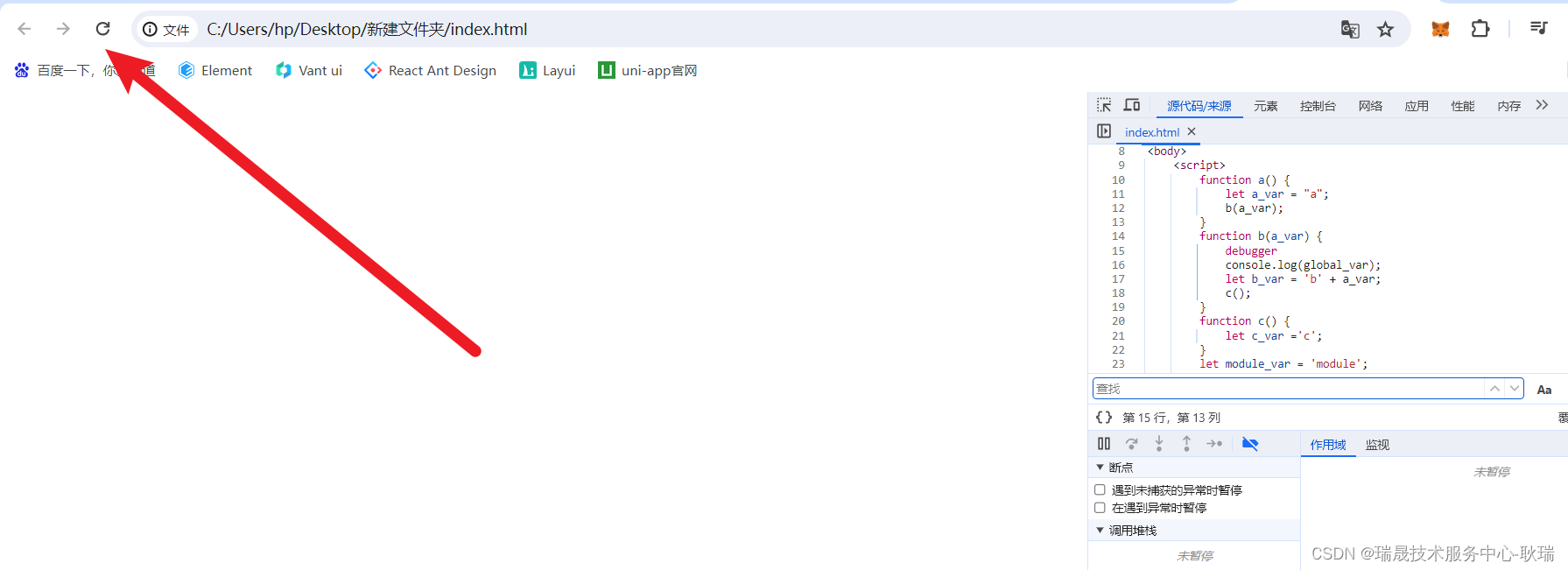
以谷歌浏览器为例 讲述 JavaScript 断点调试操作用法
今天来说个比较实用的东西 用浏览器开发者工具 对 javaScript代码进行调试 我们先创建一个index.html 编写代码如下 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content&…...

Vue前端框架--Vue工程项目问题总结{脚手架 Vue-cli}
Vue脚手架部署问题总结 我所遇到的一共两大问题 只有先执行npm install之后 才能run serve 否则会报错 vue-cli-serve不是内部或者外部的命令,也不是可运行的程序或者批处理文件的错误 1. 运行npm install会报错 2. 运行npm run serve报错 nodejs官网为 https://no…...
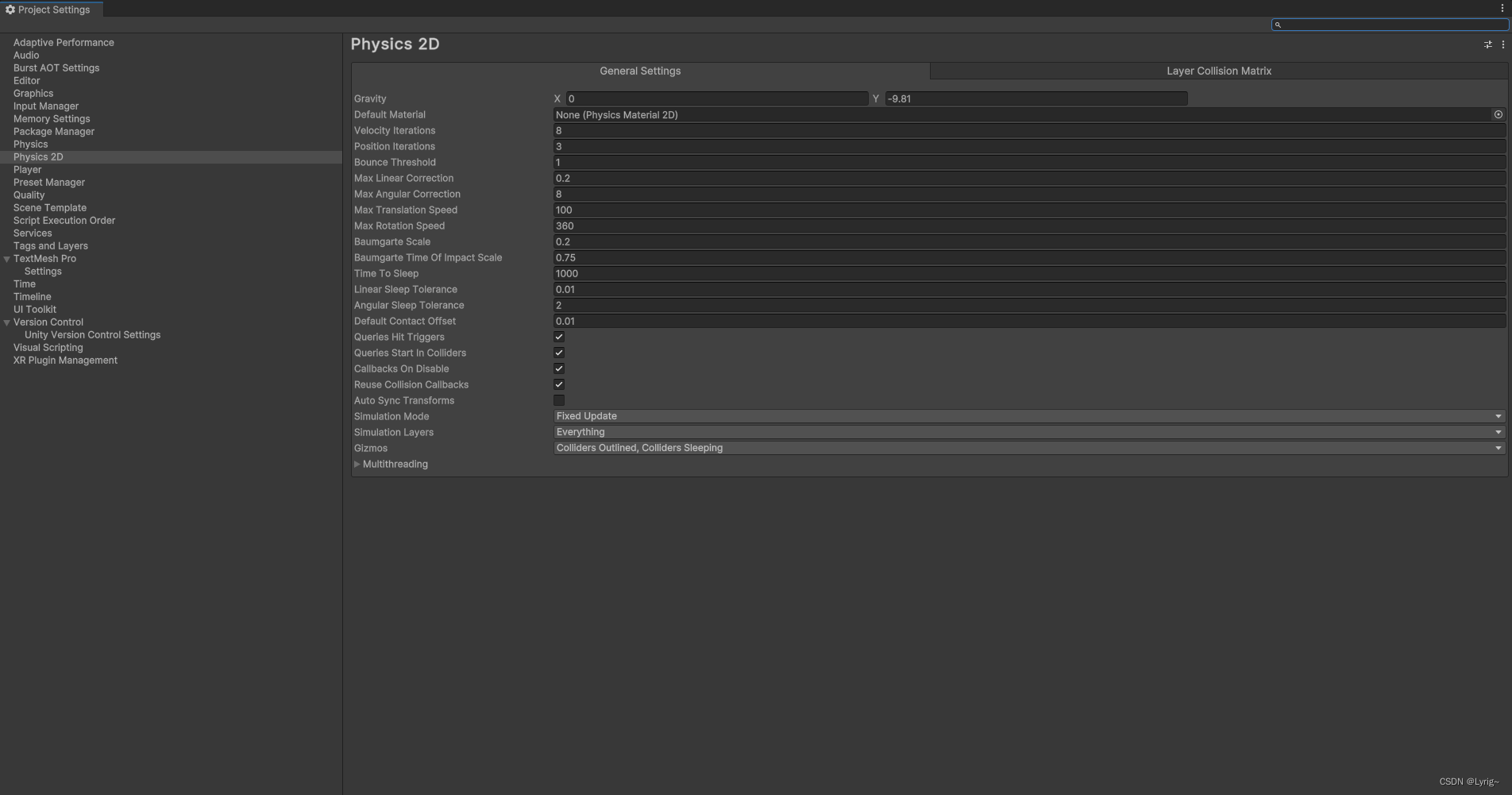
Unity2D 学习笔记 0.Unity需要记住的常用知识
Unity2D 学习笔记 0.Unity需要记住的常用知识 前言调整Project SettingTilemap相关(创建地图块)C#脚本相关程序运行函数private void Awake()void Start()void Update() Collider2D碰撞检测private void OnTriggerStay2D(Collider2D player)private void…...

vue3-应用规模化-单文件组件
单文件组件概念 Vue 的单文件组件 (即 *.vue 文件,英文 Single-File Component,简称 SFC) 是一种特殊的文件格式,使我们能够将一个 Vue 组件的模板、逻辑与样式封装在单个文件中。下面是一个单文件组件的示例: <script setup…...
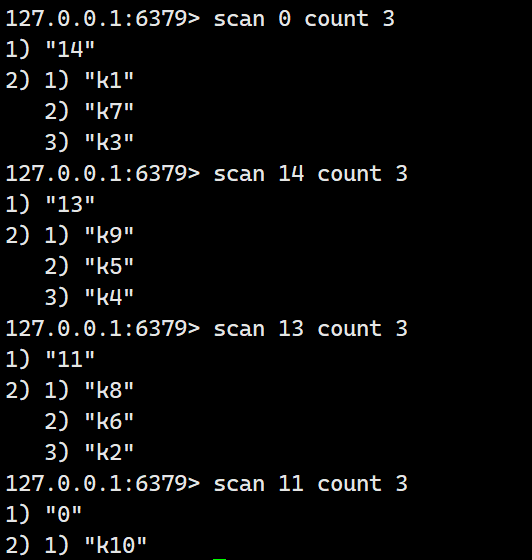
Redis -- 渐进式遍历
家,是心的方向。不论走多远,总有一盏灯为你留着。桌上的碗筷多了几双,笑声也多了几分温暖。家人团聚,是最美的风景线。时间:2024年 2月 8日 12:51:20 目录 前言 语法 示例 前言 试想一个场景,那就是在key非常多的…...
:指令解析)
使用 C++23 从零实现 RISC-V 模拟器(3):指令解析
指令解析 这章内容进一解析更多的指令,此外将解析指令的过程拆分为一个单独的类,采用表格驱动的方式,将数据和逻辑分离,降低了 if else 嵌套层数过多。 这部分依旧改动不多,只增加了七个指令。此外代码中细碎的变动没…...

CSS Selector—选择方法,和html自动——异步社区的爬取(动态网页)——爬虫(get和post的区别)
这里先说一下GET请求和POST请求: post我们平时是要加data的也就是信息,你会发现我们平时百度之类的 搜索都是post请求 get我们带的是params,是发送我们指定的内容。 要注意是get和post请求!!! 先说一下异…...
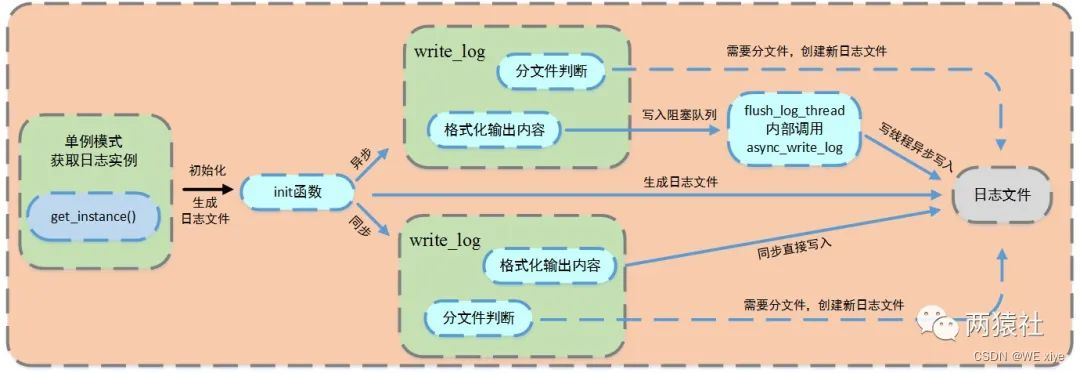
C语言 服务器编程-日志系统
日志系统的实现 引言最简单的日志类 demo按天日志分类和超行日志分类日志信息分级同步和异步两种写入方式 引言 日志系统是通过文件来记录项目的 调试信息,运行状态,访问记录,产生的警告和错误的一个系统,是项目中非常重要的一部…...

HarmonyOS 状态管理装饰器 Observed与ObjectLink 处理嵌套对象/对象数组 结构双向绑定
本文 我们还是来说 两个 harmonyos 状态管理的装饰器 Observed与ObjectLink 他们是用于 嵌套对象 或者 以对象类型为数组元素 的数据结构 做双向同步的 之前 我们说过的 state和link 都无法捕捉到 这两种数据内部结构的变化 这里 我们模拟一个类数据结构 class Person{name:…...

windows中的apache改成手动启动的操作步骤
使用cmd解决安装之后开机自启的问题 services.msc 0. 这个命令是打开本地服务找到apache的服务名称 2 .通过服务名称去查看服务的状态 sc query apacheapache3.附加上关掉和启动的命令(换成是你的服务名称) 关掉命令 sc stop apacheapache启动命令 …...
Intellij Idea的数据库工具 DataGrip
DataGrip DataGrip: IDEA自带,非常好用。智能提示很强大,快捷键跟IDEA自身一致。 如果下载不了 DataGrip,也可以直接用 IDEA 自带的。 常用的快捷键 alt8: 打开数据库Service ctrlshiftF10:打开常用的数…...
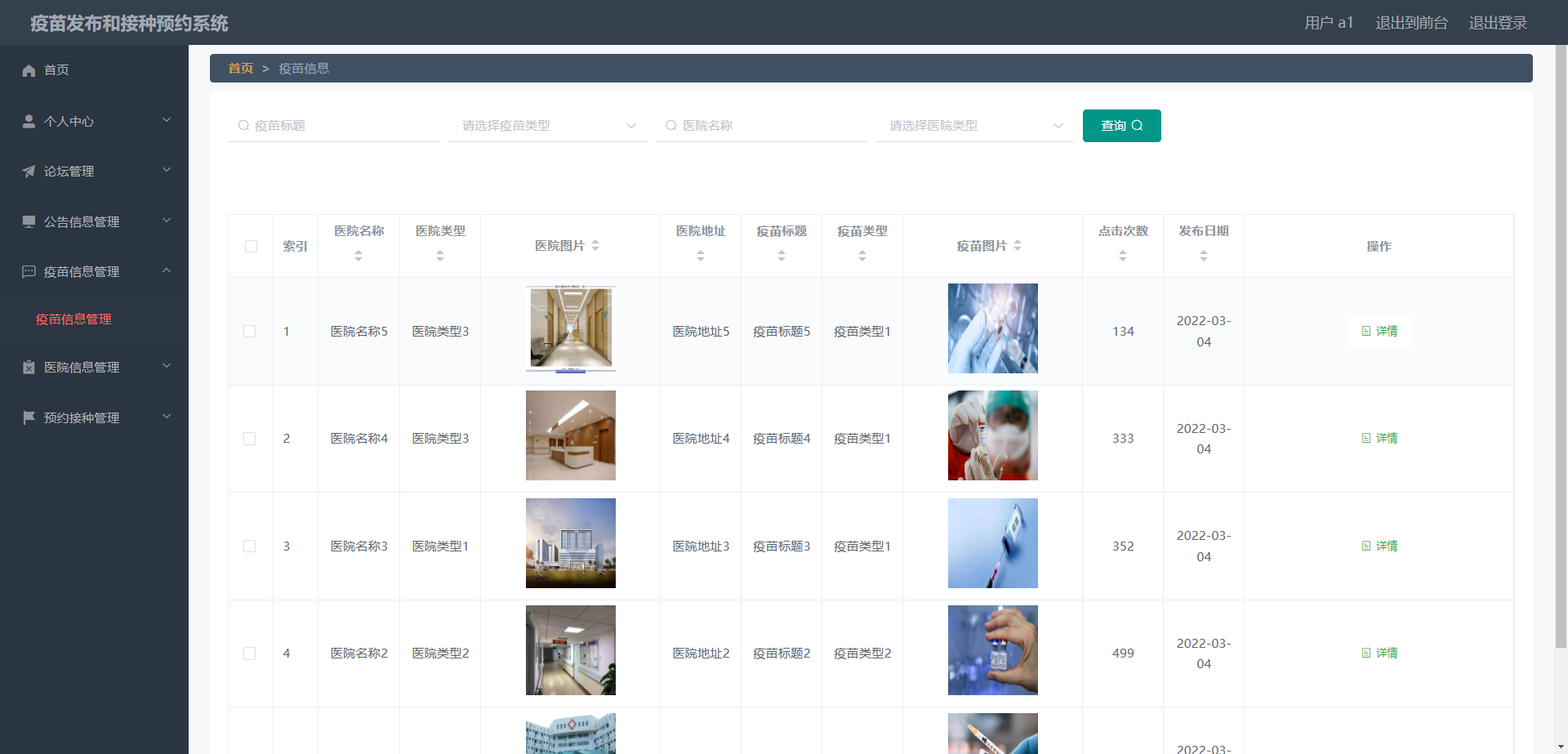
精品springboot疫苗发布和接种预约系统
《[含文档PPT源码等]精品基于springboot疫苗发布和接种预约系统[包运行成功]》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程、包运行成功! 软件开发环境及开发工具: Java——涉及技术: 前端使用技术:…...
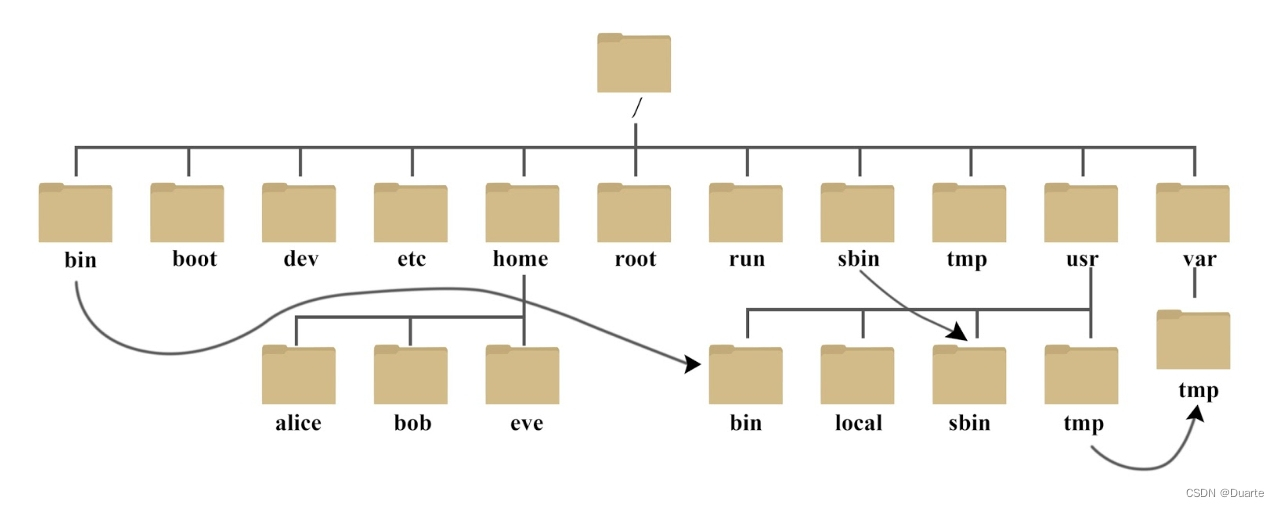
Linux快速入门
一. Linux的结构目录 1.1 Linux的目录结构 Linux为免费开源的系统,拥有众多发行版,为规范诸多的使用者对Linux系统目录的使用,Linux基金会发布了FHS标准(文件系统层次化标准)。多数的Linux发行版都遵循这一规范。 注&…...
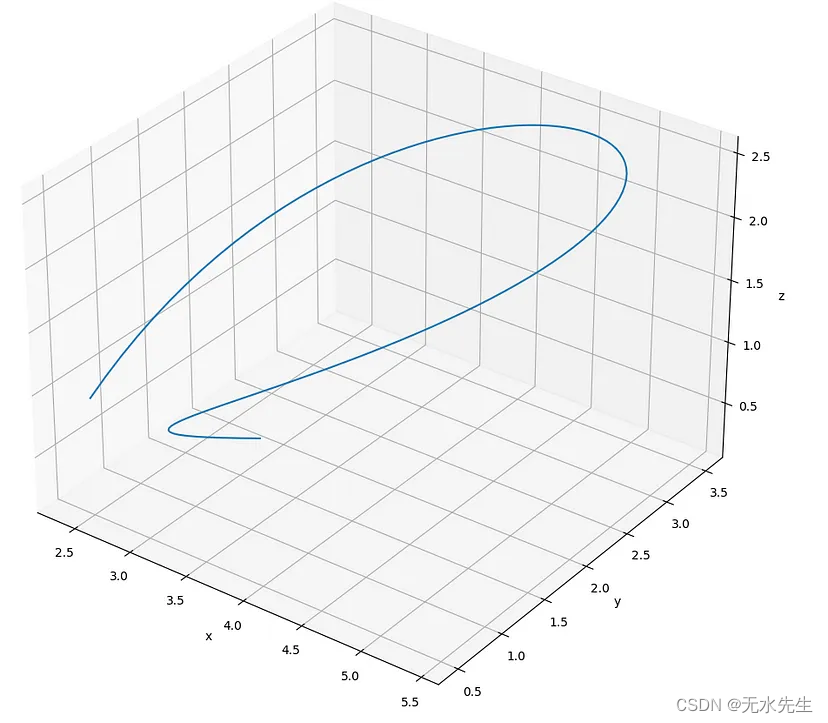
【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线
目录 一、说明二、贝塞尔曲线特征三、模拟四、全部代码如下五、资源和下载 一、说明 以下文章介绍了用 C 计算和绘制的贝塞尔曲线(2D 和 3D)。 贝塞尔曲线具有出色的数学能力来计算路径(从起点到目的地点的曲线)。曲线的形…...
python+flask+django医院预约挂号病历分时段管理系统snsj0
技术栈 后端:python 前端:vue.jselementui 框架:django/flask Python版本:python3.7 数据库:mysql5.7 数据库工具:Navicat 开发软件:PyCharm . 第一,研究分析python技术,…...

《CSS 简易速速上手小册》第9章:CSS 最佳实践(2024 最新版)
文章目录 9.1 维护大型项目的 CSS9.1.1 基础知识9.1.2 重点案例:构建一个可复用的 UI 组件库9.1.3 拓展案例 1:优化现有项目的 CSS 结构9.1.4 拓展案例 2:实现主题切换功能 9.2 BEM、OOCSS 和 SMACSS 方法论9.2.1 基础知识9.2.2 重点案例&…...
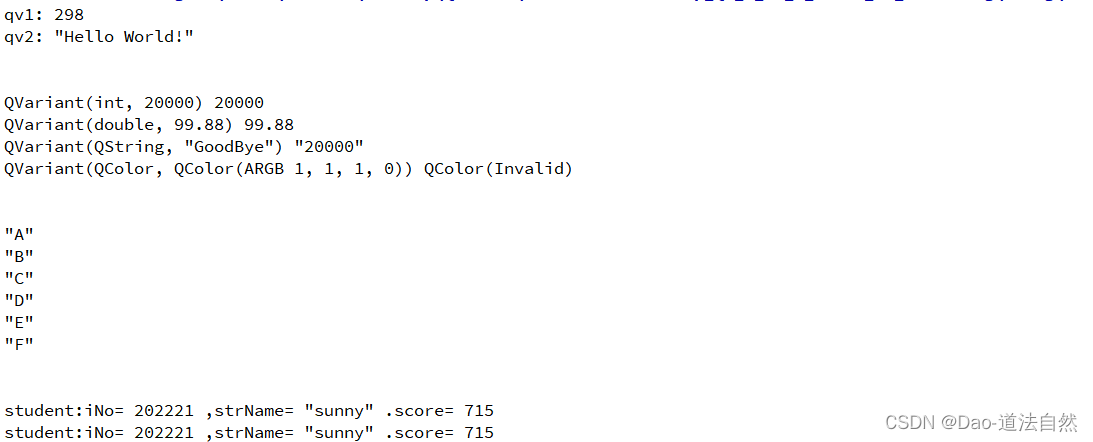
Qt QVariant类应用
QVariant类 QVariant类本质为C联合(Union)数据类型,它可以保存很多Qt类型的值,包括 QBrush,QColor,QString等等,也能存放Qt的容器类型的值。 QVariant::StringList 是 Qt 定义的一个 QVariant::type 枚举类型的变量&…...

不到1s生成mesh! 高效文生3D框架AToM
论文题目: AToM: Amortized Text-to-Mesh using 2D Diffusion 论文链接: https://arxiv.org/abs/2402.00867 项目主页: AToM: Amortized Text-to-Mesh using 2D Diffusion 随着AIGC的爆火,生成式人工智能在3D领域也实现了非常显著…...

Mac中管理多版本Jdk
1. 首先下载JDK,以jdk8和17为例 2. 打开.zprofile中添加如下内容 #java config export JAVA_8_HOME/Library/Java/JavaVirtualMachines/zulu-8.jdk/Contents/Home export JAVA_17_HOME/Library/Java/JavaVirtualMachines/zulu-17.jdk/Contents/Home#default java …...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
