位运算+leetcode(1)
基础
1.基础知识
以下都是针对数字的二进制进行操作
- >> 右移操作符
- << 左移操作符
- ~ 取反操作符
- & 有0就是0,全一才一
- | 有一才一 ,全0才0
- ^ 相同为0,相异为1
异或( ^ )运算的规律
- a ^ 0 = a
- a ^ a = 0
- a ^ b ^ c =a ^ (b ^ c)
2.基础操作
1.给一个数n, 判断它的二进制表示中的第x位是0 还是 1
( n >> x ) & 1
2.给一个数n, 将它的二进制表示中的第x位是修改为1
n = n | (1<<x)
3.给一个数n, 将它的二进制表示中的第x位是修改为0
n = n & (~ (1<<x) )
4.提取一个数( n )二进制表示最右侧的 1
这个意思:将这个数二进制形式,其中从右往左出现的第一个数字1,给保留下来,其它的位的数统统赋值给 0
n & (-n) 得到的就是
-n 表示的就是:从右往左出现的第一个数字1,它的左边区域全部变成相反的
5.干掉一个数( n )二进制表示最右侧的 1
n & ( n-1 )
n-1 表示的是:从右往左出现的第一个数字1,它的右边(包括它本身)全部变成相反
Leetcode刷题
题一:位1的个数

1. 链接
191. 位1的个数 - 力扣(LeetCode)
2.思路
直接将这个数(二进制表示形式)从右往左每次干掉一个1,然后在更新这个数,同时去统计一下总共进行了几次
3. 代码
int hammingWeight(uint32_t n) {int count=0;while(n){n=n&(n-1);count++;}return count;
}题二:比特位计数
1. 链接
338. 比特位计数 - 力扣(LeetCode)
2.思路
暴力方法
遍历 n 个数,每次统计此次所对应的数二进制里有几个1(这个就是题目一),然后再放到数组里去
动态规划
arr为我们最终返回的那个数组名
规律
- 我们让 arr [0] = 0
- 当数字为偶数时,此时该数字(n)所含一的个数与 n / 2这个数相等
- 当数字为奇数时,此时这个数(n)所含一的个数等于 n-1这个所对应的再加上1
3.代码
//暴力
class Solution {
public:vector<int> countBits(int n) {vector<int> arr(n+1);for(int i=1;i<=n;i++){int ret=0;while(i>0){i=i&(i-1);ret++;}arr[i]=ret;}return arr;}
};//动态规划
class Solution {
public:vector<int> countBits(int n) {vector<int> arr(n + 1);for (int i = 1; i <= n; i++) {if (i % 2 != 0) {arr[i] = arr[i - 1] + 1;} else {arr[i] = arr[i / 2];}}return arr;}
};题三:汉明距离

1. 链接
461. 汉明距离 - 力扣(LeetCode)
2. 思路
- 首先找到二个数中最大的数,在对最大的数,进行除二,求出其二进制的位数
- 定义一个变量count,当 ((x >> i) & 1) ! = ((y >> i) & 1) 成立时,就让count++
((x >> i) & 1) != ((y >> i) & 1) 这个是基础操作里的如何判断一个数第i位是否为 1
3.代码
class Solution {
public:int hammingDistance(int x, int y) {int _max = max(x, y);int count = 0;while (_max) {_max = _max / 2;count++;}int lenSum = 0;for (int i = 0; i < count; i++) {if (((x >> i) & 1) != ((y >> i) & 1)) {lenSum++;}}return lenSum;}
};题四:判断字符是否唯一

1.链接
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
2.思路
鸽巢原理:有n个巢,和n+1个鸽子,那么至少会有一个巢鸟的数量>1
astr 是字符串数组名
用数组来模拟哈希表
- 由于只含有小写字母,那么只要开辟一个数组长度为26的就可以
- 如果字符串的长度大于26,那么则就返回 false(鸽巢原理)
- 当字符串的长度小于26,这里的映射关系是 astr[i] - 'a'
- 先让此刻的字符进入哈希表,再去判断该字符在哈希表中位置的值是否大于1
- 若大于1,则返回 false,否则,就继续循环
用一个整数来模拟位图
- 一个整数是4个字节,一个字节是8个比特位,那么就是有36位比特位
- 由于只含有小写字母,那么一个整数就够用
- 如果字符串的长度大于26,那么则就返回 false(鸽巢原理)
- 定义一个整数biteMap,并初始化为0(保证此刻biteMap的二进制位都为0,为了方便后面判断 )
- 再去遍历这个 astr 字符串,先判断该字符在位图所在位置是否为1,
- 若为1,则返回false
- 若不为1,则将该字符在位图所在位置修改为1,在继续循环。
- 若能将这个循环结束,那么则就返回true
3.代码
法一 哈希表:
//哈希表
class Solution {
public:bool isUnique(string astr) {int hash[26] = {0};for (int i = 0; i < astr.size(); i++) {hash[astr[i] - 'a']++;if(hash[astr[i] - 'a']>1)return false;}return true;}
};法二 位图:
//位图
class Solution {
public:bool isUnique(string astr) {if (astr.size() > 26)return false;int biteMap = 0;for (auto ch : astr) {int i = ch - 'a';if (((biteMap >> i) & 1) == 1)return false;biteMap = biteMap | (1 << i);}return true;}
};相关文章:

位运算+leetcode(1)
基础 1.基础知识 以下都是针对数字的二进制进行操作 >> 右移操作符<< 左移操作符~ 取反操作符 & 有0就是0,全一才一 | 有一才一 ,全0才0^ 相同为0,相异为1 异或( ^ )运算的规律 a ^ 0 a a ^ a 0a ^ b ^ c a ^ (b …...

如何在 JavaScript 中比较两个日期 – 技术、方法和最佳实践
在 JavaScript 中,您可以使用 date 对象有效地处理应用程序中的日期、时间和时区。 Date 对象可帮助您有效地操作数据、处理各种与日期相关的任务,并在创建实际应用程序时执行一些计算。 (本文内容参考:java567.com)…...

【More Effective C++】条款17:考虑使用lazy evaluation
含义:将计算拖延到必须计算的时候,以下为4个场景 优点:避免不必要的计算,节省成本 缺点: 管理复杂性:可能会增加代码复杂性,特别是在多线程环境中需要正确处理同步和并发问题。性能开销&…...

深入探索Pandas读写XML文件的完整指南与实战read_xml、to_xml【第79篇—读写XML文件】
深入探索Pandas读写XML文件的完整指南与实战read_xml、to_xml XML(eXtensible Markup Language)是一种常见的数据交换格式,广泛应用于各种应用程序和领域。在数据处理中,Pandas是一个强大的工具,它提供了read_xml和to…...

如何在我们的模型中使用Beam search
在上一篇文章中我们具体探讨了Beam search的思想以及Beam search的大致工作流程。根据对Beam search的大致流程我们已经清楚了,在这我们来具体实现一下Beam search并应用在我们的seq2seq任务中。 1. python中的堆(heapq) 堆是一种特殊的树形…...

PKI - 借助Nginx 实现Https 服务端单向认证、服务端客户端双向认证
文章目录 Openssl操系统默认的CA证书的公钥位置Nginx Https 自签证书1. 生成自签名证书和私钥2. 配置 Nginx 使用 HTTPS3. 重启 Nginx 服务4. 直接访问5. 不验证证书直接访问6. 使用server.crt作为ca证书验证服务端解决方法1:使用 --resolve 参数进行请求域名解析解…...
WebSocket原理详解
目录 1.引言 1.1.使用HTTP不断轮询 1.2.长轮询 2.websocket 2.1.概述 2.2.websocket建立过程 2.3.抓包分析 2.4.websocket的消息格式 3.使用场景 4.总结 1.引言 平时我们打开网页,比如购物网站某宝。都是点一下列表商品,跳转一下网页就到了商品…...

在面试中如何回复擅长vue还是react
当面试官问及这个问题的时候,我们需要思考面试官是否是在乎你是掌握vue还是react吗??? 在大前端的一个环境下,当前又有AI人工智能的加持辅助,我们是不是要去思考企业在进行前端岗位人员需求的时候…...
使用Vue.js输出一个hello world
导入vue.js <script src"https://cdn.jsdelivr.net/npm/vue2/dist/vue.js"></script> 创建一个标签 <div id"app">{{message}}</div> 接管标签内容,创建vue实例 <script type"text/javascript">va…...
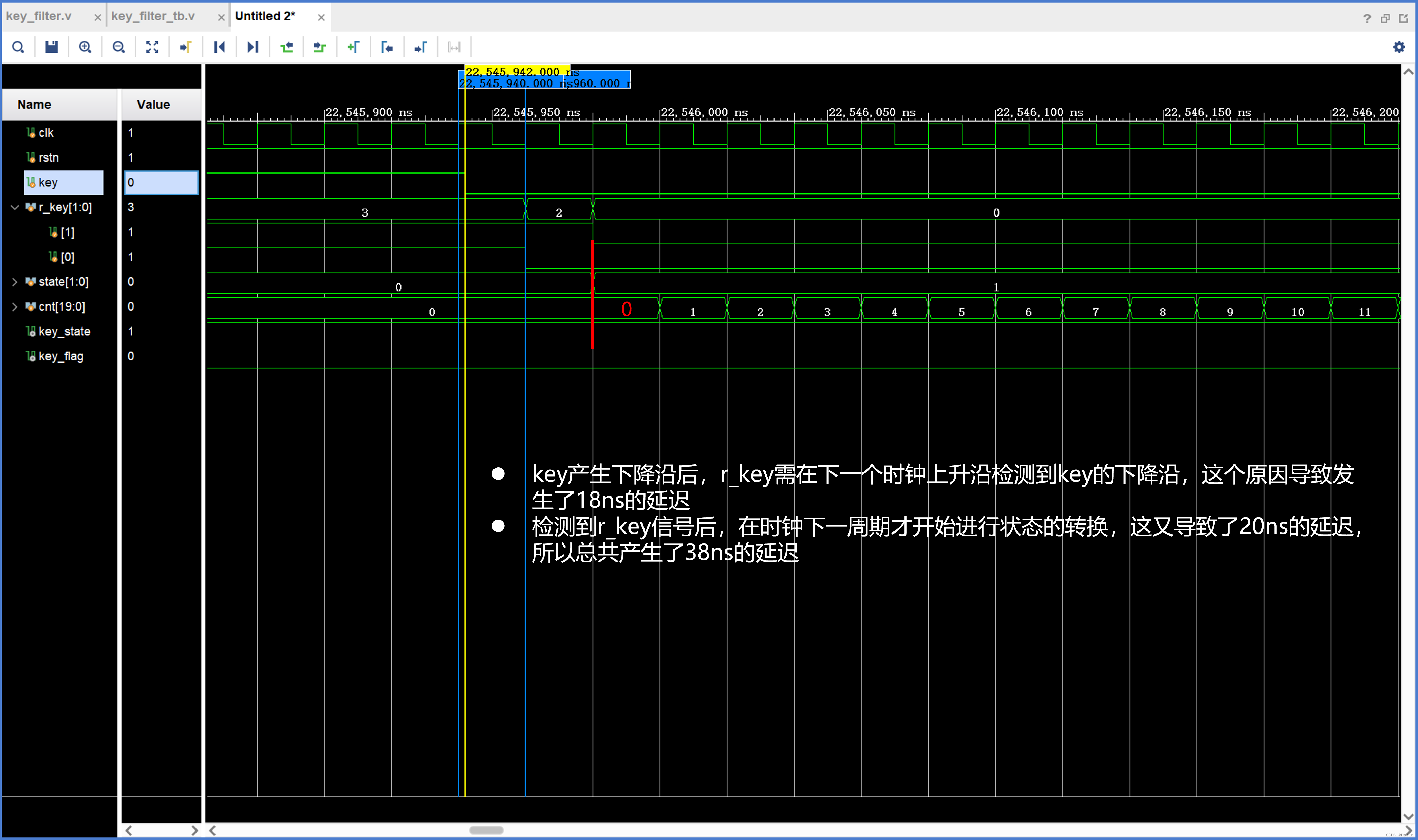
15 ABC基于状态机的按键消抖原理与状态转移图
1. 基于状态机的按键消抖 1.1 什么是按键? 从按键结构图10-1可知,按键按下时,接点(端子)与导线接通,松开时,由于弹簧的反作用力,接点(端子)与导线断开。 从…...

λ-矩阵的多项式展开
原文链接 定义. 对于 m n m \times n mn 的 λ \lambda λ-矩阵 A ( λ ) [ a 11 ( λ ) . . . a 1 n ( λ ) ⋮ ⋮ a m 1 ( λ ) . . . a m n ( λ ) ] \mathbf{A}(\lambda)\begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda)\\ \vdots & & \vdo…...

如何在PDF 文件中删除页面?
查看不同的工具以及解释如何在 Windows、Android、macOS 和 iOS 上从 PDF 删除页面的步骤: PDF 是最难处理的文件格式之一。曾经有一段时间,除了阅读之外,无法用 PDF 做任何事情。但是今天,有许多应用程序和工具可以让您用它们做…...
)
蓝桥杯官网填空题(质数拆分)
问题描述 将 2022 拆分成不同的质数的和,请问最多拆分成几个? 答案提交 本题为一道结果填空的题,只需要算出结果后,在代码中使用输出语句将结果输出即可。 运行限制 import java.util.Scanner;public class Main {static int …...
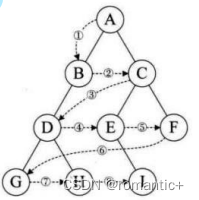
【数据结构】二叉树的顺序结构及链式结构
目录 1.树的概念及结构 1.1树的概念 1.2树的相关概念 编辑 1.3树的表示 1.4树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1二叉树的概念 2.2现实中的二叉树 编辑 2.3特殊的二叉树 2.4二叉树的性质 2.5二叉树的存储结…...

海外IP代理:解锁网络边界的实战利器
文章目录 引言:正文:一、Roxlabs全球IP代理服务概览特点:覆盖范围:住宅IP真实性:性价比:在网络数据采集中的重要性: 二、实战应用案例一:跨境电商竞品分析步骤介绍:代码示…...

如何写好一个简历
如何编写求职简历 论Java程序员求职中简历的重要性 好简历的作用 在求职过程中,一份好的简历是非常重要的,它甚至可以直接决定能否被面试官认可。一份出色或者说是成功的个人简历,最根本的作用是能让看这份简历的人产生一定要见你的强烈愿…...
【AutoML】AutoKeras 进行 RNN 循环神经网络训练
由于最近这些天都在人工审查之前的哪些问答数据,所以迟迟都没有更新 AutoKeras 的训练结果。现在那部分数据都已经整理好了,20w 的数据最后能够使用的高质量数据只剩下 2k。这 2k 的数据已经经过数据校验并且对部分问题的提问方式和答案内容进行了不改变…...

H12-821_74
74.在某路由器上查看LSP,看到如下结果: A.发送目标地址为3.3.3.3的数据包时,打上标签1026,然后发送。 B.发送目标地址为4.4.4.4的数据包时,不打标签直接发送。 C.当路由器收到标签为1024的数据包,将把标签…...

有趣儿的组件(HTML/CSS)
分享几个炫酷的组件,起飞~~ 评论区留爪,继续分享哦~ 文章目录 1. 按钮2. 输入3. 工具提示4. 单选按钮5. 加载中 1. 按钮 HTML: <button id"btn">Button</button>CSS: button {padding: 10px 20px;text-tr…...
1、深度学习环境配置相关下载地址整理(cuda、cudnn、torch、miniconda、pycharm、torchvision等)
一、深度学习环境配置相关: 1、cuda:https://developer.nvidia.com/cuda-toolkit-archive 2、cudnn:https://developer.nvidia.com/rdp/cudnn-archive 4、miniconda:https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/?C…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
