DS:树及二叉树的相关概念
创作不易,兄弟们来波三连吧!!
一、树的概念及结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。

1、有一个特殊的结点,称为根结点,根节点没有前驱结点
2、除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继(每个孩子只能有一个父亲,每个父亲可以有多个孩子)
3、因此,树是递归定义的。(树可以分成2部分,1部分是父亲节点,1部分是N颗子树,如果子树不是叶子,那么子树可以继续分成父节点和子树)
注意:树结构中,子树之间不能有交集,否则就不是树结构!!
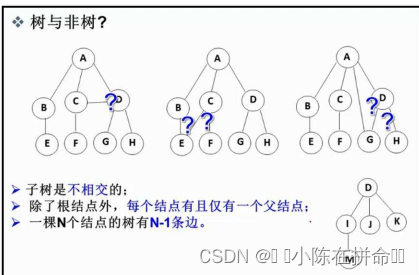
1.2 树的相关名词
树的相关名词是依照树加上人类的亲缘关系表述的!
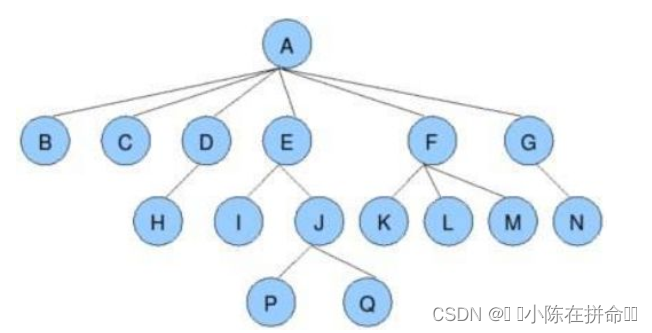
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
以上标红的是博主认为比较重要的。
1.3 树的表示方法
树的结构相比较于以往的其他结构就比较复杂了,要存储起来表示就比较有难度,不仅要保存值域,也要保存节点和节点之间的关系。
如果我们知道节点的度,那么我们就可以根据这个度来决定我们的结构体中需要有多少个孩子指针!!但是如果我们不知道节点的度,我们就有了以下方法来表示:
1.3.1 双亲表示法
实现:定义数组结构存放树的结点,每个结点含两个域:
数据域:存放结点本身数据信息。
双亲域:指示本结点的双亲结点在数组中的位置。(可以存放双亲的下标,也可以存放双亲的指针)

这样的存储结构,根据结点parent指针很容易找到它的双亲结点,所用时间复杂度为O(1),直到parent为-1时,找到了树的根结点,但是如果我们想要知道孩子的节点,那么唯一的方法就是遍历!!
特点:找双亲容易,找孩子难
1.3.2 孩子表示法
具体办法是:把每个结点的孩子结点排列起来,看成是一个线性表,以单链表作存储结构,则n个结点有n个孩子链表(叶子结点的孩子链表为空),然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中

特点:找孩子易,找双亲难
这样的结构对于我们要查找某个结点的某个孩子,或者找某个结点的兄弟,只需要查找这个结点的孩子单链表即可。对于遍历整棵树也是很方便的,对头结点的数组循环即可。
1.3.3 孩子双亲表示法
就是把上面两种方法结合一下

即在链表表头再增加一个数据域存储双亲的下标,用空间换取方便!
1.3.4 左孩子右兄弟表示法
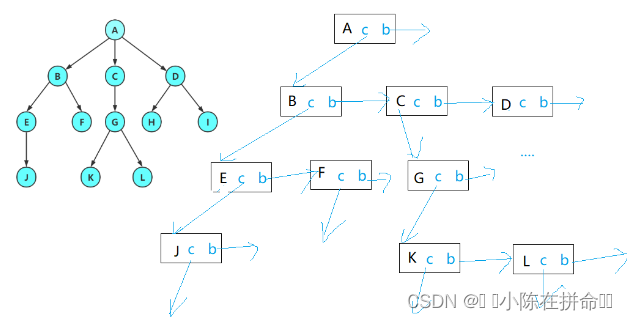
但是我们用的最多的还是左孩子右兄弟法,因为相关的结构体只需要1个指向兄弟的指针,1个指向第一个孩子的指针,一个数据域就可以解决问题了!
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

1.4 树在实际中的应用
就是文件系统中的目录树结构!!
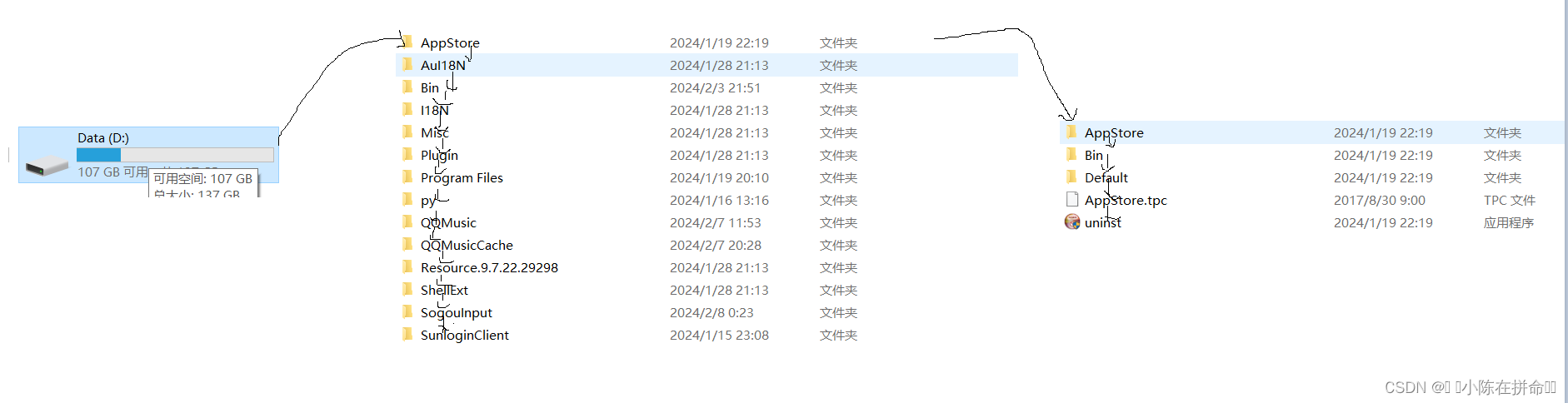
我们打开磁盘,在底层就是通过磁盘地孩子指针找到第一个孩子,然后再通过第一个孩子的兄弟指针开始逐个逐个遍历后面的兄弟节点,才能把整个目录给列举出来,
如果我们新建一个文件夹,就是让该文件目录下的兄弟节点指向NULL的文件指向这个新建文件,然后新建文件的兄弟指针指向NULL,当然这个也要看情况,有时候文件排序的方式也是不同的
二、二叉树的概念及结构
实际中我们的树一般只用在这个目录树结构,而我们最常用的是树中的一个比较特殊的群体——二叉树
2.1 二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

二叉树的特点:
1、 二叉树不存在度大于2的节点
2、二叉树的左右子树不能颠倒
2.2 特殊的二叉树
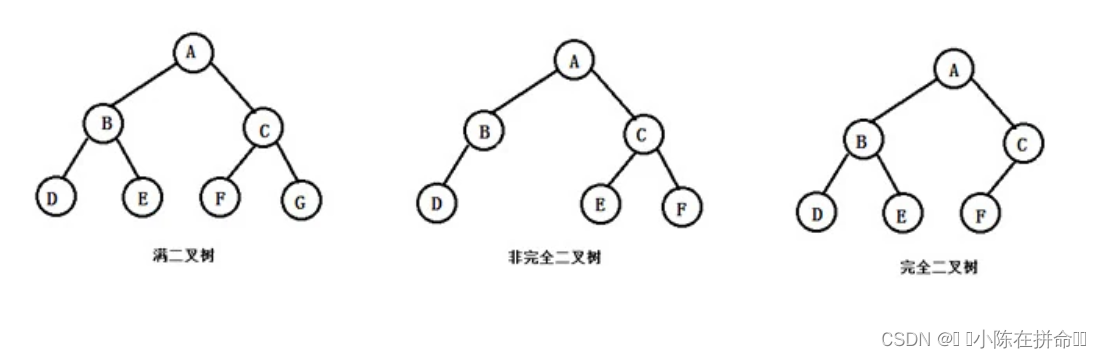
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1

3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有总是有n0=n2+1

4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log(N+1)(ps: 是log以2
为底,n+1为对数)
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.4 二叉树的存储方式
2.4.1 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
一般来说,顺序存储只适用于完全二叉树!!
2.4.2 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链。
先介绍到这里了!!
关于存储方式的详细介绍,后面会发布文章进行学习的
感谢支持!!
相关文章:

DS:树及二叉树的相关概念
创作不易,兄弟们来波三连吧!! 一、树的概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,…...
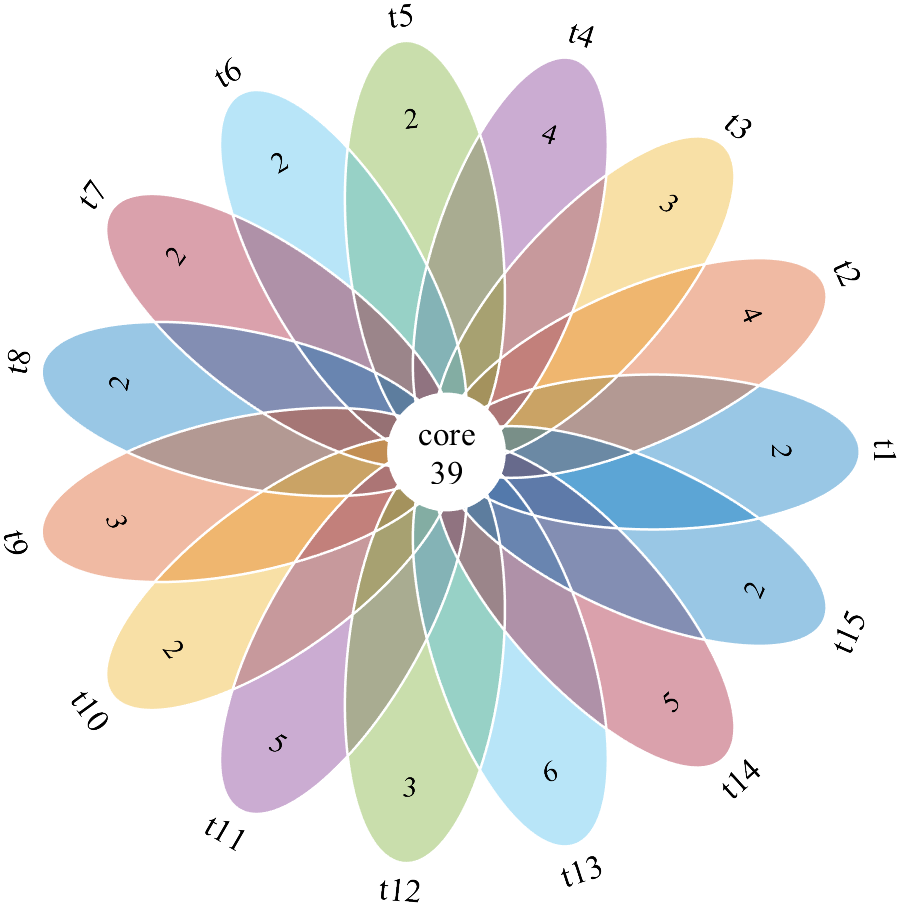
MATLAB | 情人节画个花瓣venn图?
之前七夕节情人节各种花,相册,爱心啥的都快画够了,今年画个花瓣韦恩图? 花瓣上的数字是仅属于该类的样本数,而中心的数字是属于每一类的样本数 教程部分 0 数据准备 % 给组起名t1 t2 t3...t15 setName compose(t%d,…...

[日常使用] Shell常用命令
Shell是什么? Shell简介 Shell是操作系统的外壳,是用户与操作系统内核之间的主要接口。它接收用户的命令并将其传递给内核执行,然后将执行结果返回给用户。Shell不仅是一个命令解释器,也是一种强大的编程语言。常见的Shell分为图…...
)
QT+OSG/osgEarth编译之八十七:osgdb_p3d+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_p3d)
文章目录 一、osgdb_p3d介绍二、文件分析三、pro文件四、编译实践一、osgdb_p3d介绍 P3DXML是Panda3D引擎中使用的一种文件格式,用于描述3D场景的层次结构和属性。它是一种基于XML(eXtensible Markup Language)的文本格式,可以被Panda3D引擎读取和解析。 P3DXML文件包含了…...
寒假 day13
1.请编程实现二维数组的杨慧三角 #include<stdio.h> #include<string.h> int main(int argc, const char *argv[]) { int n,i,j;printf("please enter n:");scanf("%d",&n);int arr[n][n];for(i0;i<n;i){for(j0;j<i;j){if(j0 || ij…...

探索微信小程序的奇妙世界:从入门到进阶
文章目录 一、什么是微信小程序1.1 简要介绍微信小程序的定义和特点1.2 解释小程序与传统应用程序的区别 二、小程序的基础知识2.1 微信小程序的架构2.2 微信小程序生命周期的理解2.3 探索小程序的目录结构和文件类型 三、小程序框架和组件3.1 深入了解小程序框架的核心概念和原…...
-std::forward_list)
容器库(4)-std::forward_list
std::forward_list是可以从任何位置快速插入和移除元素的容器,不支持快速随机访问,只支持正向迭代。 本文章的代码库: https://gitee.com/gamestorm577/CppStd 成员函数 构造、析构和赋值 构造函数 可以用元素、元素列表、迭代器或者另…...

Netty Review - 服务端channel注册流程源码解析
文章目录 PreNetty主从Reactor线程模型服务端channel注册流程源码解读入口 serverBootstrap.bind(port) 源码流程图 Pre Netty Review - ServerBootstrap源码解析 Netty Review - NioServerSocketChannel源码分析 Netty主从Reactor线程模型 Netty 使用主从 Reactor 线程模型…...

冒泡排序平均需要跑多少趟:拉马努金Q函数初探
摘要: 拉马努金Q函数在算法分析中的应用,初步体验 【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,阅读更多原创文章】 我的网站:潮汐朝夕的生活实验室 我的公众号:算法题刷刷 我的知乎&#x…...
Shell 学习笔记(三)-shell变量
Shell 语言是一种动态类型和弱类型语言, 因此,在Shell中无需显示地声明变量, 且变量的类型会根据不同的操作符而发生变化. 静态类型语言: 在程序编译期间就确定变量类型的语言, 如java, C等 动态类型语言: 在程序运行期间才确定变量类型的语言, 如PHP, Python等. 一 shell变量…...

新冠:2022和2024两次新冠感染的对比
第一次 2022年底第一次放开管控,95%以上的人都感染了一次奥密克戎 症状 第一天:流涕,咽痛。 第二天:高烧40度,全身疼痛,动不了。没有胃口,头晕想吐。 吃了白加黑退烧药,清开灵颗粒…...

笔记:《NCT全国青少年编程能力等级测试教程Python语言编程二级》
NCT全国青少年编程能力等级测试教程Python语言编程二级 ISBN:9787302565857 绪论 专题1 模块化编程 考查方向 考点清单 考点 模块化编程 (一)模块化编程思想:结构清晰、降低复杂度;提高代码复用率;易于扩展、维护,方便阅读、优化。 …...

顶级思维方式——认知篇五(思想的觉醒)
目录 1、 女性的地位觉醒 2、电视剧《天道》之高人思维:丁元英为什么讲“人间黑白颠倒”? 3、 创业公司, 更应该大胆的创新. 4、 做到一定职务的时候, 你一定想到在你这个地位上你要做什么 1、 女性的地位觉醒 过去引以为鉴的例子&…...

面试技术栈 —— 2024网易雷火暑期实习真题
面试技术栈 —— 2024网易雷火暑期实习真题 1. 最长递增子序列。2. 集中限流和单机限流你觉得哪个好?3. redis部署服务器配置,为什么不用哨兵?4. 讲讲分布式session的原理。5. 数据库:表数据量大了,如何分表࿱…...
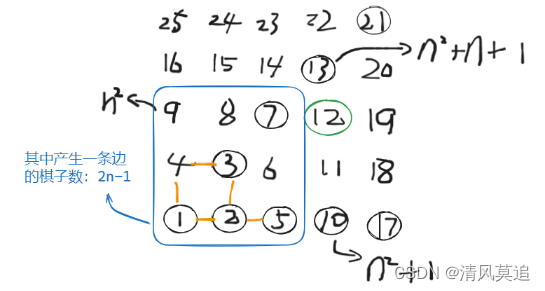
【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6) 完稿时间:2024-2-13 比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/ 相关资料: 1、出题人题解:“蓝桥杯双周赛第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com) 2、矩阵快速幂&…...
-yum二进制部署)
docker (二)-yum二进制部署
yum安装docker(Linux) 安装环境:CentOS 7.9 一 如果之前安装了旧版docker,请先删除 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...
)
【深度学习】S2 数学基础 P2 线性代数(下)
目录 范数的意义范数的数学意义范数之于深度学习的意义 L1 范数与 L2 范数L1 范数L2 范数 小结 本节博文是线性代数第二部分,主要内容为 L 1 L1 L1 范数与 L 2 L2 L2 范数;有关线性代数基础知识,请访问:【深度学习】S2 数学基础…...

【软考高级信息系统项目管理师--考试内容大纲篇】
🚀 作者 :“码上有前” 🚀 文章简介 :软考高级–信息系统项目管理师 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 软考高级信息系统项目管理师--考试内容大纲篇 1.信息化发展2.信息技术发展3.信息系…...

C语言——枚举类型
📝前言: 在之前的文章中我们已经讲解了自定义类型中的结构体类型和联合体类型,现在我们再充分学习一下C语言中的枚举类型: 1,什么是枚举类型 2,枚举类型的定义和变量的声明 3,对变量进行赋值 &a…...

linux---内存管理
一 虚拟内存 即使是现代操作系统中,内存依然是计算机中很宝贵的资源,看看你电脑几个T固态硬盘,再看看内存大小就知道了。 为了充分利用和管理系统内存资源,Linux采用虚拟内存管理技术,利用虚拟内存技术让每个进程都有…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

