使用playwright进行自动化端到端测试
项目希望能接入自动化端到端测试提高可靠性,发现微软的 playwright 还挺好用的,推荐一下,顺便说下遇到的一些难点以及最佳实践。
难点
- 登录
- 项目不能帐号密码登录,只能扫二维码
-
临时方案是先自己扫码保存 cookie 用于测试,大概几天后才过期。可以用 codegen 搭配 save-storage 命令保存 cookie
npx playwright codegen github.com/microsoft/playwright --save-storage=auth.json可以保存cookie 到 auth.json,用npx playwright --load-storage=auth.json命令即可加载,也可以在测试文件中加载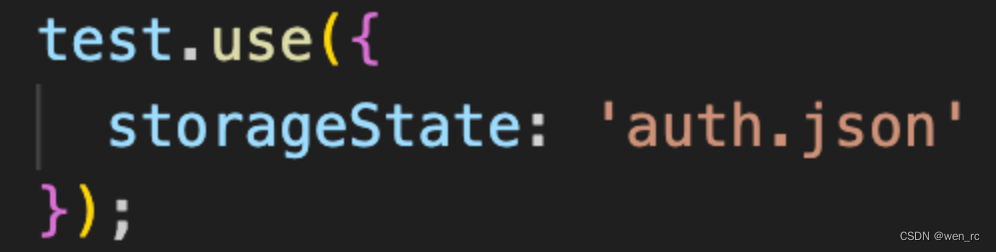
-
长期的方案应该是跟后台同学 py,搞个长期有效的 cookie 或者测试帐号,可以只在测试环境、内网生效,规避外网风险
-
- 项目不能帐号密码登录,只能扫二维码
- 支付,项目有支付环节,目前有扫二维码支付、网银支付、转账,扫码应该是比较好测试的
-
暂时想到的方案是生成支付二维码后,截图推送给触发测试的人去扫码支付

-
对测试号配置一分钱测试商品方便测试
-
如果能确保支付环节不会出错,支付是外部稳定的第三方模块,也可以考虑用免费订单跳过支付环节?
-
最佳实践
https://playwright.nodejs.cn/docs/best-practices
测试理念
- 测试用户能看到的,不要依赖实现细节
- 测试尽可能隔离
- 避免测试第三方依赖
- 有数据库相关的要考虑数据变化是否影响测试
- 视觉回归测试要考虑操作系统和浏览器版本
tips
- 使用定位器的时候
- 支持链式,使用过滤搜索小范围
- 优先用面向用户的属性,而不是 css 选择器
- 用能够适应 dom 变化的定位器,比如ARIA role、 ARIA 参数和可访问的名称
page.getByRole('tab', { name: '其它' }) - 可以用codegen 功能来生成定位器,如
npx playwright codegen github.com/microsoft/playwright,他会帮你找到最适合的定位器(太好用了!)
- 使用web first断言(assertions),playwright 会等待,直到条件达成
- 比如发了个取消请求,语气能看到取消成功的提示,可以这样写
await expect(page.getByText('取消成功')).toBeVisible(),toBeVisible()这种断言会等待和重试 - await要写在 expect 前面,如果像
expect(await page.getByText('welcome').isVisible()).toBe(true);这样,会立即检查定位器能否找到并返回结果,不会去等待重试
- 比如发了个取消请求,语气能看到取消成功的提示,可以这样写
- 调试
- 安装 VSCode 插件调试
- trace viewer 能看截图,能看时间线
- test 加 ui 命令能可视化测试过程
- 在配置里可以很方便的测多几种浏览器
- 及时更新 playwright 依赖
- CI 中跑测试
- 测试文件接入 lint
- 并行跑测试,playwright 对于一个文件的测试是按顺序跑的,可同时跑多个文件,如果对单个文件也想并行跑,可以这样写
- 用 soft 断言,可以不终止测试
expect.soft
其他
无障碍访问
Web 无障碍访问 (也称为 a11y) 是指创建可供任何人使用的网站的做法——无论是身患某种障碍、通过慢速的网络连接访问、使用老旧或损坏的硬件,还是仅处于某种不方便的环境。例如,在视频中添加字幕可以帮助失聪、有听力障碍或身处嘈杂环境而听不到手机的用户。同样地,确保文字样式没有处于太低的对比度,可以对低视力用户和在明亮的强光下使用手机的用户都有所帮助。
ARIA roles
相关文章:

使用playwright进行自动化端到端测试
项目希望能接入自动化端到端测试提高可靠性,发现微软的 playwright 还挺好用的,推荐一下,顺便说下遇到的一些难点以及最佳实践。 难点 登录 项目不能帐号密码登录,只能扫二维码 临时方案是先自己扫码保存 cookie 用于测试&#…...

ES实战-相关性搜索
ES打分机制 1.TF-IDF 词频-逆文档频率 2.Okapi BM25 3.随机性分歧- DFR相似度 4.基于信息 - IB相似度 5.LM Dirichlet 相似度 6.LM Jelinek Mercer相似度 解释一个查询的结果集 curl -XPOST localhost:9200/get-together/_search?pretty -H Content-Type: application/json -…...
MQTT的学习与应用
文章目录 一、什么是MQTT二、MQTT协议特点三、MQTT应用领域四、安装Mosquitto五、如何学习 MQTT 一、什么是MQTT MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息传输协议,设计用于在低带宽、不稳定的网络环境中进行高效的通信…...
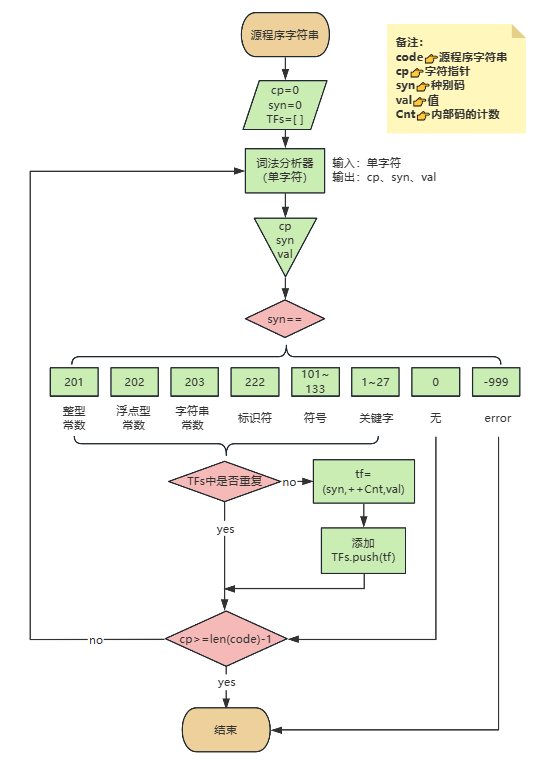
编译原理实验1——词法分析(python实现)
文章目录 实验目的实现定义单词对应的种别码定义输出形式:三元式python代码实现运行结果检错处理 总结 实验目的 输入一个C语言代码串,输出单词流,识别对象包含关键字、标识符、整型浮点型字符串型常数、科学计数法、操作符和标点、注释等等。…...

C语言——oj刷题——模拟实现库函数strlen
目录 方法一:迭代法 方法二:递归法 方法三:指针算术法 方法四:汇编指令法 当我们使用C语言进行字符串操作时,经常会用到库函数strlen来获取字符串的长度。strlen函数的作用是计算一个以null字符结尾的字符串的长度…...
对进程与线程的理解
目录 1、进程/任务(Process/Task) 2、进程控制块抽象(PCB Process Control Block) 2.1、PCB重要属性 2.2、PCB中支持进程调度的一些属性 3、 内存分配 —— 内存管理(Memory Manage) 4、线程(Thread)…...

「数据结构」线性表
定义和基本操作 定义:相同数据类型的 n ( n ≥ 0 ) n(n \ge 0) n(n≥0)个数据元素的有限序列,其中n为表长,当n0时线性表是一个空表一般表示: L ( a 1 , a 2 , … … , a i , a i 1 , a n ) L(a_1,a_2,……,a_i,a_{i1},a_n) L(a…...

GEE:关于在GEE平台上进行回归计算的若干问题
作者:CSDN _养乐多_ 记录一些在Google Earth Engine (GEE)平台上进行机器学习回归计算的问题和解释。 文章目录 一、回归1.1 问:GEE平台上可以进行哪些机器学习回归算法?1.2 问:为什么只有这四种…...

Vivado -RAM
ip_ram 定义了一个名为ip_ram的模块,该模块具有以下端口: sys_clk:系统时钟输入。 sys_rst_n:系统复位输入。 module ip_ram( input sys_clk, input sys_rst_n);wire ram_en ; wire ram_wea …...
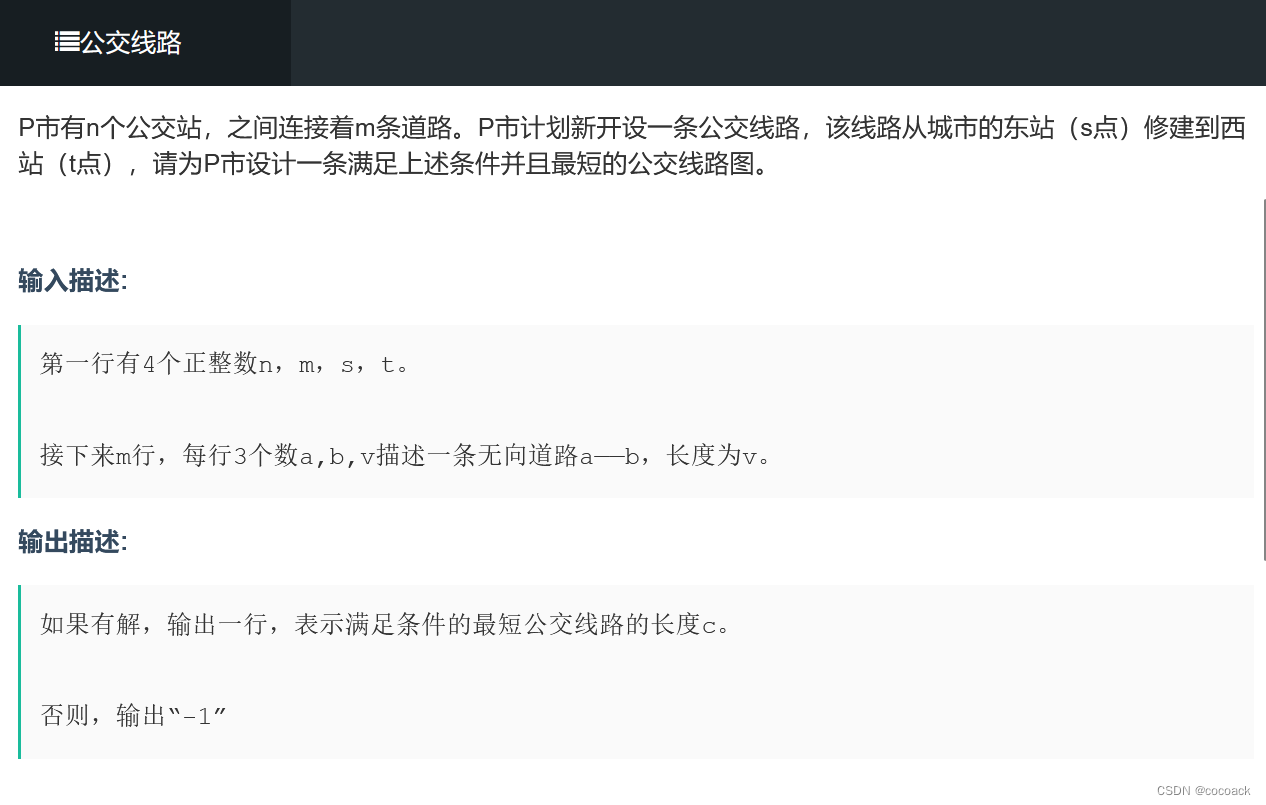
备战蓝桥杯---图论之最短路dijkstra算法
目录 先分个类吧: 1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。 2.边权全部相等,直接BFS即可 3.单源点最短路 从一个点出发,到达其他顶点的最短路长度。 Dijkstra算法&#x…...
)
C#系列-C#实现秒杀功能(14)
在C#中实现商品秒杀功能,通常需要考虑并发控制、数据库事务、缓存策略、限流措施等多个方面。下面是一个简单的示例,演示了如何使用C#和数据库来实现一个基本的商品秒杀功能。 首先,假设你有一个商品表(Product)和一个…...

Java ‘Elasticsearch‘ 操作
依赖 <!-- https://mvnrepository.com/artifact/org.springframework.boot/spring-boot-starter-data-elasticsearch --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch</ar…...

【AI视野·今日NLP 自然语言处理论文速览 第七十八期】Wed, 17 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Wed, 17 Jan 2024 (showing first 100 of 163 entries) Totally 100 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Deductive Closure Training of Language Models for Coherence, Accur…...

实验5-4 使用函数计算两点间的距离
本题要求实现一个函数,对给定平面任意两点坐标(x1,y1)和(x2,y2),求这两点之间的距离。 函数接口定义: double dist( double x1, double y1, double x2, double y2 );其中用户传入的参数为平面上两个点的坐标(x1, y1)和(x2, y2)&…...
【JavaEE】_JavaScript(Web API)
目录 1. DOM 1.1 DOM基本概念 1.2 DOM树 2. 选中页面元素 2.1 querySelector 2.2 querySelectorAll 3. 事件 3.1 基本概念 3.2 事件的三要素 3.3 示例 4.操作元素 4.1 获取/修改元素内容 4.2 获取/修改元素属性 4.3 获取/修改表单元素属性 4.3.1 value…...

ARM交叉编译搭建SSH
首先搭建好arm-linux交叉编译环境,开发板和主机可以ping通。 一、下载需要的源码 下载zlib: zlib-1.2.3.tar.gz 下载ssl: openssl-0.9.8d.tar.gz 下载ssh: openssh-4.6p1.tar.gz 二、交叉编译 新建目录/home/leo/ssh,并且将三个源码复制到该目录下。…...

###51单片机学习(2)-----如何通过C语言运用延时函数设计LED流水灯
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 目录 一. 延时函数的生成 1.通过延时计算器得到延时函数 2.可赋值改变…...

回归预测模型:MATLAB多项式回归
1. 多项式回归模型的基本原理 多项式回归是线性回归的一种扩展,用于分析自变量 X X X与因变量 Y Y Y之间的非线性关系。与简单的线性回归模型不同,多项式回归模型通过引入自变量的高次项来增加模型的复杂度,从而能够拟合数据中的非线性模式。…...

「计算机网络」数据链路层
数据链路层的地位:网络中的主机、路由器等都必须实现数据链路层信道类型 点对点信道:使用一对一的点对点通信方式广播信道 使用一对多的广播通信方式必须使用专用的共享信道协议来协调这些主机的数据发送 使用点对点信道的数据链路层 数据链路和帧 链…...

【Linux】Ubuntu 22.04 升级 nodejs 到 v18
Ubuntu 22.04 已经安装的nodejs 版本 nodejs is already the newest version (12.22.9~dfsg-1ubuntu3.3). 删除以前的 nodejs 版本: 1. sudo apt remove nodejs rooterp:~# sudo apt remove nodejs Reading package lists... Done Building dependency tree..…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
