【C语言】数据结构#实现堆

目录
(一)堆
(1)堆区与数据结构的堆
(二)头文件
(三)功能实现
(1)堆的初始化
(2)堆的销毁
(3)插入数据
(4)删除堆顶的数据
(5)得到堆顶的数据
(6)判断堆是否为空
(7)得到堆内数据个数
正文开始:
(一)堆
(1)堆区与数据结构的堆
堆区和数据结构中的堆是两个不同的概念。
堆区 (Heap) :堆区是计算机内存中的一部分,用于存储动态分配的内存空间。在程序运行时,堆区用于存储使用 new 或 malloc 等方法分配的内存空间,在程序运行结束后,由程序员手动释放。堆区是一块较大的内存区域,用于存储动态分配的数据。堆区的大小可以动态增长或缩小,具有较高的灵活性。堆区的访问速度较慢,但能够存储较大的数据。
数据结构中的堆:在数据结构中,堆是一种特殊的树状结构,具有以下特点:
- 堆是一个完全二叉树,即除了最底层外,其他层都是满的,最底层的结点从左到右连续排列。
- 堆中的每个结点的值都大于等于(或小于等于)其子结点的值,根结点是树中最大(或最小)的结点。
- 堆可以分为最大堆和最小堆,最大堆的根结点是整个堆中最大的元素,最小堆的根结点是整个堆中最小的元素。
在数据结构中,堆通常用于实现优先队列(Priority Queue)和堆排序(Heap Sort)等算法。堆的插入和删除操作的时间复杂度都为 O(log n),其中 n 是堆中元素的个数。
(二)头文件
STL(Standard Template Library)是C++标准库中的一个组件,提供了一系列的通用数据结构和算法,以及一些函数模板,用于简化C++程序的开发。STL包括了容器(Containers)、算法(Algorithms)和迭代器(Iterators)三个主要部分。
容器(Containers):STL提供了多种容器,包括向量(vector)、链表(list)、双端队列(deque)、集合(set)、映射(map)等。这些容器提供了不同的数据结构和操作,方便了数据的存储和处理。
算法(Algorithms):STL提供了一系列的算法,包括排序、查找、合并、变序、计数等等。这些算法可以对容器中的元素进行操作,使得程序更加高效和简洁。
迭代器(Iterators):STL的迭代器是一个泛型指针,用于遍历容器中的元素。迭代器提供了一种统一的访问容器元素的方式,使得算法可以独立于容器而使用。
本文根据Cpp的STL来实现堆的功能,包括堆的初始化,销毁,插入数据,删除堆顶的数据,得到堆顶的数据,判断堆是否为空,得到堆内数据个数等七个功能接口。
本文基于顺序表实现堆;
这里不加解释的给出头文件,根据头文件实现堆的功能:
命名:Heap.h
#pragma once#include<stdio.h> #include<stdlib.h> #include<stdbool.h> #include<assert.h>typedef int HPDatatype;typedef struct Heap {HPDatatype* a;//存储数据的数组int size; //堆内数据的个数int capacity; //顺序表的容量 }HP;//初始化 void HPinit(HP* php);//销毁 void HPDestroy(HP* php);//插入数据 void HPpush(HP* php, HPDatatype x);//删除数据,规定删除堆顶的数据 void HPpop(HP* php);//得到堆顶数据 HPDatatype HPtop(HP* php);//判空 bool HPempty(HP* php);//数据个数 int HPsize(HP* php);
(三)功能实现
(1)堆的初始化
堆的初始化
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
将数组置空,顺序表的大小与容量置0;
//初始化 void HPinit(HP* php) {assert(php);php->a = NULL;php->capacity = php->size = 0; }
(2)堆的销毁
堆的销毁
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
释放掉动态申请的顺序表内的数组,顺序表的大小与容量置0;
//销毁 void HPDestroy(HP* php) {assert(php);free(php->a);php->capacity = php->size = 0;}
(3)插入数据
插入数据
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
其次判断数组内数据是否满了
——如果顺序表容量等于数组的大小,代表数据满了,那么进行扩容。Newcapacity的赋值通过三目操作符实现:如果capacity为初始值0,Newcapacity赋值为4,否则赋值为2*capacity。如果realloc申请失败,打印错误信息并返回。若申请成功,压入数据。
——如果数据没有满,直接在数组中插入数据,由于插入的数据不一定与原数据成堆,所以要进行向上调整;
调整需要交换,于是提前给出交换的功能接口:
交换
//传址交换 void Swap(HPDatatype* p1, HPDatatype* p2) {HPDatatype tem = *p1;*p1 = *p2;*p2 = tem; }
什么是向上调整?
堆在逻辑上是二叉树,在物理上实际上是数组,数组的下标如下:
在堆中,有一个规律:
- 父节点下标 = (子节点下标 - 1) / 2;
- 左子节点下标 = (父结点下标 * 2) + 1;
- 右子节点下标 = (父结点下标 * 2) + 2;
于是,我们可以通过一个节点的下标,找到他的父和子的下标 ;
本文以实现小堆为例
向上调整
将新插入的节点与其父节点比较,如果新节点小于父结点,两节点交换值,继续迭代进行;
直到新节点的值大于等于父结点,或者已经比到了根节点才停止;
//push实现小堆的向上调整 void AdgustUP(HPDatatype* a,int child) {int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child],&a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} }
插入数据
//插入数据 void HPpush(HP* php, HPDatatype x) {assert(php);//数据满,realloc扩容,得到新的大容量顺序表if (php->capacity == php->size){int Newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDatatype* tem = (HPDatatype*)realloc(php->a, Newcapacity * sizeof(HPDatatype));if (tem == NULL){perror("realloc fail!");return;}php->a = tem;php->capacity = Newcapacity;}//数据不满,直接插入php->a[php->size] = x;php->size++;//向上调整AdgustUP(php->a,php->size-1); }
(4)删除堆顶的数据
删除数据
删除数据规定的是删除堆顶的数据;
函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
如何删除?
-直接删除,由于二叉树的兄弟节点是没有大小关系的,如果直接删除根节点,那么所有节点的下标减一,这意味着原来的的二叉树的结构就被完全破坏了,接下来只能重新建堆,代价太大。
-先交换堆顶与最后一个数据,然后删除最后一个数据(其实就是原堆顶数据),然后进行向下调整;
这样既没有完全破换二叉树的结构,只有一个数据需要调整位置,又操作简便只需size--即可。
向下调整
思路与向上调整基本一致;
//小堆向下调整——找小 void AdgustDown(HPDatatype* a, int n, int parent) {//假设左孩子小int child = parent * 2 + 1;while (child < n){//如果右孩子小,假设不成立if (child + 1 < n && a[child] > a[child + 1]){child++;}//此时,child表示较小的孩子if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}删除数据
//删除数据,规定删除堆顶的数据 void HPpop(HP* php) {assert(php);//交换堆顶与最后一个数据Swap(&php->a[0], &php->a[php->size - 1]);//删除堆顶的数据php->size--;//向下调整AdgustDown(php->a, php->size,0);}
(5)得到堆顶的数据
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
其次,堆不为空,通过assert断言实现;
直接返回堆顶的数据即可;
//得到堆顶数据 HPDatatype HPtop(HP* php) {assert(php);assert(!HPempty(php));return php->a[0]; }
(6)判断堆是否为空
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
直接返回判断表达式的值即可;(若为空,返回真(1);否则返回假(0))
//判空 bool HPempty(HP* php) {assert(php);return php->size == 0; }
(7)得到堆内数据个数
首先,函数接收的指针(被传入的地址)不为空(否则无法进行解引用操作),通过assert断言实现;
直接返回堆内数据个数即可;
//数据个数 int HPsize(HP* php) {assert(php);return php->size; }
完~
未经作者同意禁止转载
相关文章:
【C语言】数据结构#实现堆
目录 (一)堆 (1)堆区与数据结构的堆 (二)头文件 (三)功能实现 (1)堆的初始化 (2)堆的销毁 (3)插入数据 …...
AES加密中的CBC和ECB
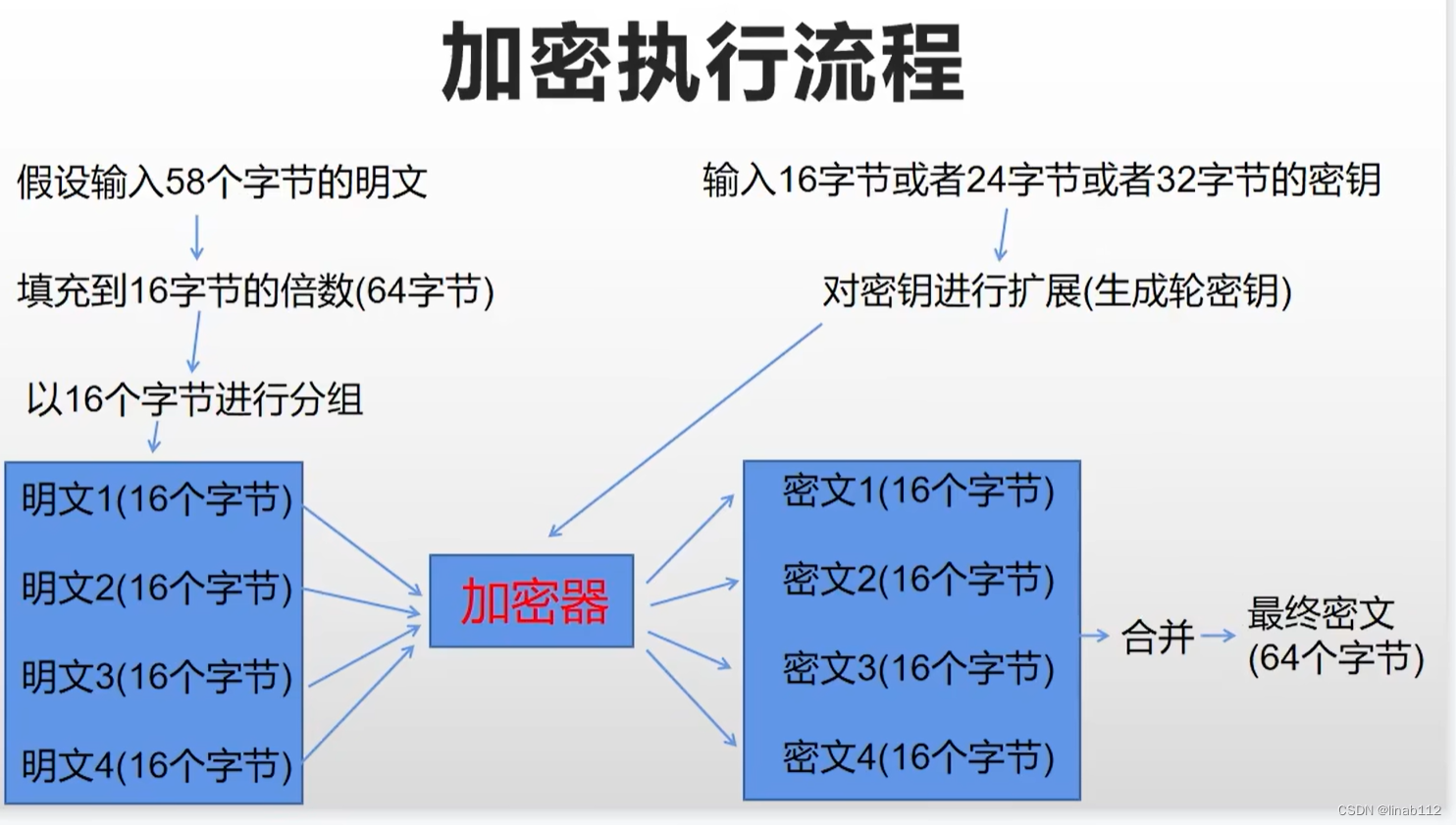
目录 1.说明 2.ECB模式(base64) 3.CBC模式 4.总结 1.说明 AES是常见的对称加密算法,加密和解密使用相同的密钥,流程如下: 主要概念如下: ①明文 ②密钥 用来加密明文的密码,在对称加密算…...

【C++】类和对象(四)
前言:在类和对象中,我们走过了十分漫长的道路,今天我们将进一步学习类和对象,类和对象这块荆棘地很长,各位一起加油呀。 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:高质量&a…...

XGB-5: DART Booster
XGBoost 主要结合了大量的回归树和一个小的学习率。在这种情况下,早期添加的树是重要的,而晚期添加的树是不重要的。 Vinayak 和 Gilad-Bachrach 提出了一种将深度神经网络社区的 dropout 技术应用于梯度提升树的新方法,并在某些情况下报告了…...
HiveSQL——不使用union all的情况下进行列转行
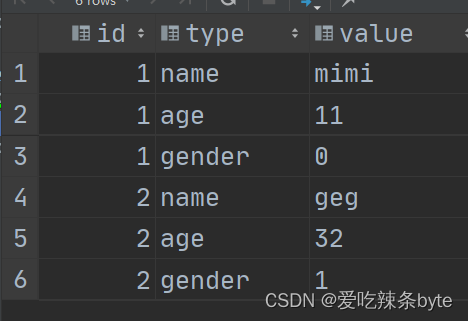
参考文章: HiveSql一天一个小技巧:如何不使用union all 进行列转行_不 union all-CSDN博客文章浏览阅读881次,点赞5次,收藏10次。本文给出一种不使用传统UNION ALL方法进行 行转列的方法,其中方法一采用了concat_wsposexplode()方…...
Python环境下基于指数退化模型和LSTM自编码器的轴承剩余寿命预测
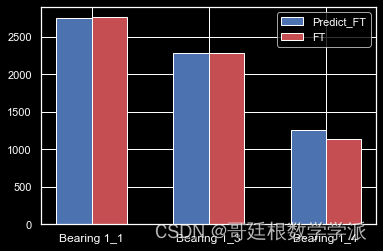
滚动轴承是机械设备中关键的零部件之一,其可靠性直接影响了设备的性能,所以对滚动轴承的剩余使用寿命(RUL)进行预测是十分必要的。目前,如何准确地对滚动轴承剩余使用寿命进行预测,仍是一个具有挑战的课题。对滚动轴承剩余寿命评估…...
)
无人机竞赛视觉算法开发流程开源计划(询问大家意见)
本科中参加过一系列的无人机机器人竞赛,像电赛、工训赛、机器人大赛这些,有一些比较常用的方案打算开源一下。现在读研了,也算是对本科的一个总结,但是还是想看看大家意见,大家有什么需求可以在评论区说,我…...
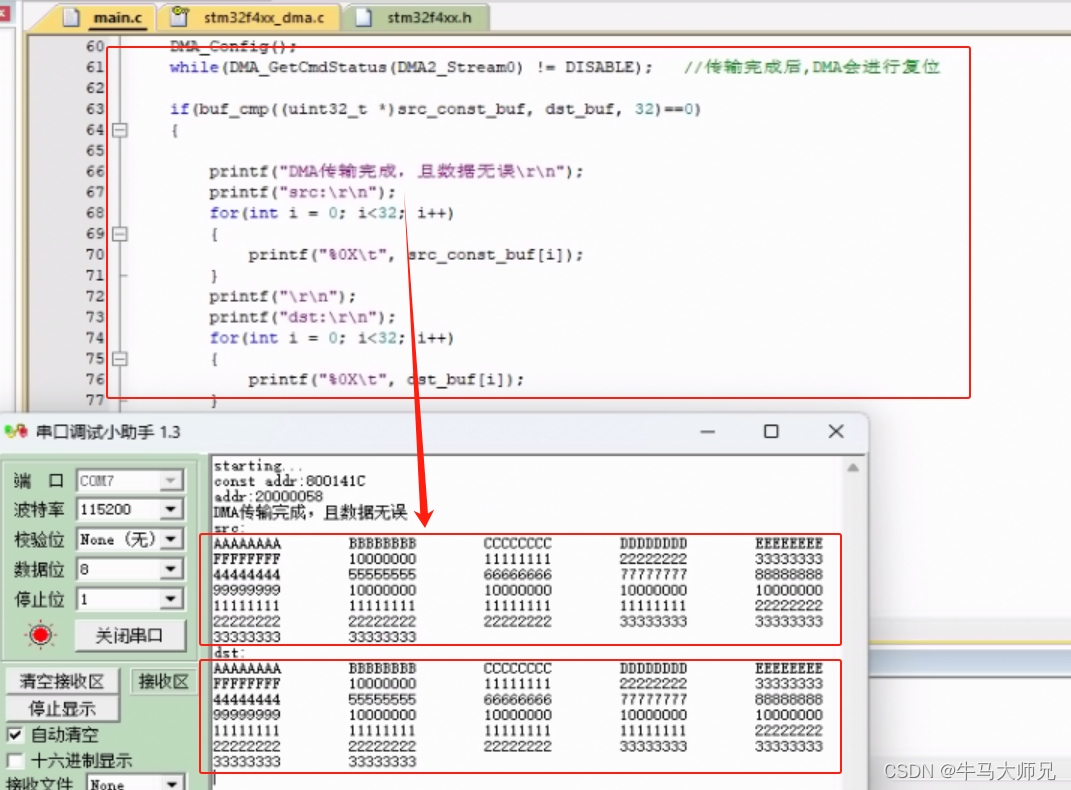
DMA直接内存访问,STM32实现高速数据传输使用配置
1、DMA运用场景 随着智能化、信息化的不断推进,嵌入式设备的数据处理量也呈现指数级增加,因此对于巨大的数据量处理的情况时,必须采取其它的方式去替CPU减负,以保证嵌入式设备性能。例如SD卡存储器和音视频、网络高速通信等其它情…...
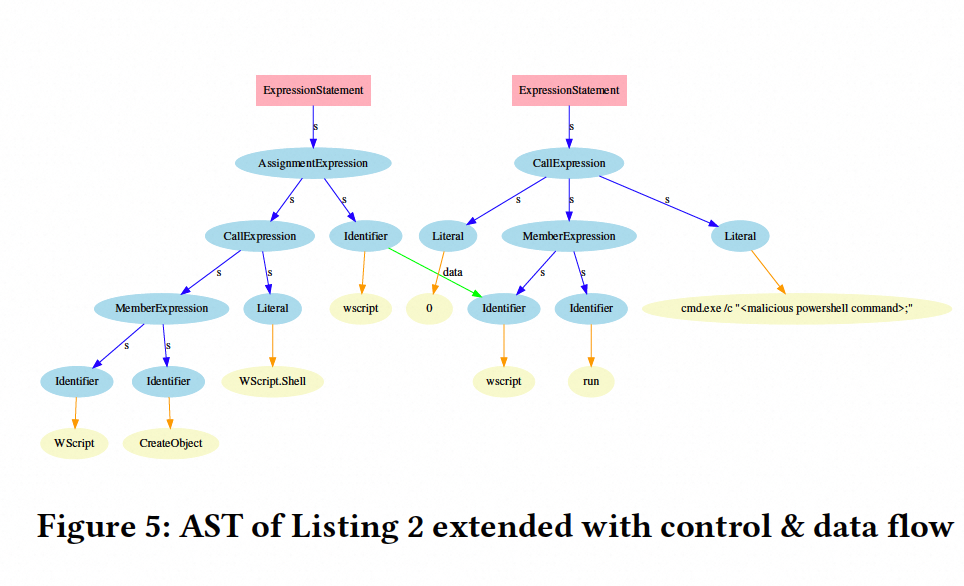
Web安全研究(六)
文章目录 HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs文章结构Introjs obfuscationmethodologyExample HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs CCS 2019 CISPA 恶意软件领域,基于学习的系统已经非常流行&am…...

python3 中try 异常调试 raise 异常抛出
一、什么是异常? 异常即是一个事件,该事件会在程序执行过程中发生,影响了程序的正常执行。 一般情况下,在Python无法正常处理程序时就会发生一个异常。 异常是Python对象,表示一个错误。 当Python脚本发生异常时我…...

Java中的序列化是什么?如何实现对象的序列化和反序列化?请解释Serializable接口的作用是什么?请解释transient关键字的作用是什么?为什么会使用它?
Java中的序列化是指将对象转换为字节序列的过程,以便可以在网络上传输或将其保存到持久存储介质中。反序列化则是将字节序列重新转换回对象的过程。Java提供了一种称为序列化(Serialization)的机制来实现对象的序列化和反序列化。 要实现对象…...

二维差分---三维差分算法笔记
文章目录 一.二维差分构造差分二维数组二维差分算法状态dp求b[i][j]数组的二维前缀和图解 二.三维前缀和与差分三维前缀和图解:三维差分核心公式图解:模板题 一.二维差分 给定一个原二维数组a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数…...

D. Divisible Pairs
思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。 代码: voi…...

【教程】Kotlin语言学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 文章目录 【Kotlin语言学习】系列文章一、基本数据…...

react 插槽
问题开发当中会经常出现组件十分相似的组件,只有一部分是不同的 解决: 父组件:在引用的时候 import { Component } from "react"; import Me from "../me";const name <div>名称</div> class Shoop extends Compone…...

Linux运用fork函数创建进程
fork函数: 函数原型: pid_t fork(void); 父进程调用fork函数创建一个子进程,子进程的用户区父进程的用户区完全一样,但是内核区不完全一样;如父进程的PID和子进程的PID不一样。 返回值: RETURN VALUEO…...

Pytest测试技巧之Fixture:模块化管理测试数据
在 Pytest 测试中,有效管理测试数据是提高测试质量和可维护性的关键。本文将深入探讨 Pytest 中的 Fixture,特别是如何利用 Fixture 实现测试数据的模块化管理,以提高测试用例的清晰度和可复用性。 什么是Fixture? 在 Pytest 中&a…...

设计模式-职责链模式Chain of Responsibility
职责链模式 一、原理和实现二、实现方式1) 使用链表实现2) 使用数组实现3) 扩展 作用:复用和扩展,在实际的项目开发中比较常用。在框架开发中,我们也可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下&…...

书生浦语大模型实战营-课程作业(3)
下载sentence_transformer的代码运行情况。sentence_transformer用于embedding(转向量) 本地构建持久化向量数据库。就是把txt和md文件抽取出纯文本,分割成定长(500)后转换成向量,保存到本地,称…...

考研英语单词25
Day 25 bench n.长凳 elastic n.橡皮圈,松紧带 a.灵活的 “e-last 延伸出去” disaster n.灾难,灾祸【disastrous a.灾难性的,极坏的】 deadly a.致命的,极端的,势不两立的 hike n.徒步旅行&…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

