UVA1449 Dominating Patterns 题解
UVA1449 Dominating Patterns 题解
板子题诶。
解法
AC 自动机模板题,因为数据范围比较小,所以不加拓扑排序优化建图即可通过本题。这里简单介绍一下拓扑排序优化建图。
在查找时,每次都暴力的条 f a i l fail fail 指针是很消耗时间的,查找到了一个字符串可能意味着找到了多个字符串,例如我们有两个模式串 bc 和 abc,我们找到了串 abc,这同时意味着我们找到了串 bc,如果每次都去跳失配边的话效率过低,我们可以在找到一个模式串后打标记,最后进行拓扑排序求得最后的答案。
为什么可以使用拓扑排序?
因为失配边都是有向边,而失配边的起点一定比终点深度要深,而且不会存在自环。所以所有失配边所构成的图是一个有向无环图。
另外,这里建图不用真的把边都建出来,统计一下入度就行。
代码
#include<bits/stdc++.h>
namespace fast_IO
{/*** 快读快写。*/
};
using namespace fast_IO;
class AC_auto
{
private:#define LEN 1000001#define N 200int a[LEN][26],val[LEN],flag[LEN],fail[LEN],ind[LEN],cnt,tmp;int ans[N],map[N];std::deque<int> q;
public:inline AC_auto(){memset(fail,0,sizeof(fail)),memset(val,0,sizeof(val)),memset(flag,0,sizeof(flag));memset(a,0,sizeof(a)),memset(ind,0,sizeof(ind));memset(ans,0,sizeof(ans)),memset(map,0,sizeof(map));cnt=1;}inline void clear(){for(int i=0;i<=cnt;i++) memset(a[i],0,sizeof(a[i])),val[i]=flag[i]=fail[i]=ind[i]=0;memset(ans,0,sizeof(ans)),memset(map,0,sizeof(map));cnt=1;}inline void build(){for(int i=0;i<26;i++) a[0][i]=1;q.push_back(1);while(!q.empty()){tmp=q.front();q.pop_front();for(int i=0;i<26;i++)if(a[tmp][i])fail[a[tmp][i]]=a[fail[tmp]][i],ind[fail[a[tmp][i]]]++,q.push_back(a[tmp][i]);else a[tmp][i]=a[fail[tmp]][i];}}inline void add(std::string st,int pos){int now=1;for(int i=0;i<st.size();i++){if(!a[now][st[i]-'a']) a[now][st[i]-'a']=++cnt;now=a[now][st[i]-'a'];}if(!flag[now]) flag[now]=pos;map[pos]=flag[now];}inline void ask(std::string st){int now=1;for(int i=0;i<st.size();i++) now=a[now][st[i]-'a'],val[now]++;}inline void topo_sort(){for(int i=1;i<=cnt;i++) if(!ind[i]) q.push_back(i);while(!q.empty()){tmp=q.front(),q.pop_front();ans[flag[tmp]]=val[tmp],val[fail[tmp]]+=val[tmp];if(!(--ind[fail[tmp]])) q.push_back(fail[tmp]);}}inline std::vector<int> output(const int l,const int r){std::vector<int> ret;int maxi=0;for(int i=l;i<=r;i++)if(ans[map[i]]>maxi) maxi=ans[map[i]],ret.clear(),ret.push_back(i);else if(ans[map[i]]==maxi) ret.push_back(i);out<<maxi<<'\n';return ret;}
};
AC_auto ac_auto;
int n;
std::string s,t[200];
std::vector<int> v;
int main()
{while(1){in>>n;if(n==0) break;ac_auto.clear();for(int i=1;i<=n;i++) in>>t[i],ac_auto.add(t[i],i);ac_auto.build(),in>>s,ac_auto.ask(s),ac_auto.topo_sort(),v=ac_auto.output(1,n);for(int i=0;i<v.size();i++) out<<t[v[i]]<<'\n';}fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);return 0;
}
相关文章:

UVA1449 Dominating Patterns 题解
UVA1449 Dominating Patterns 题解 板子题诶。 解法 AC 自动机模板题,因为数据范围比较小,所以不加拓扑排序优化建图即可通过本题。这里简单介绍一下拓扑排序优化建图。 在查找时,每次都暴力的条 f a i l fail fail 指针是很消耗时间的&…...
【C语言】数据结构#实现堆
目录 (一)堆 (1)堆区与数据结构的堆 (二)头文件 (三)功能实现 (1)堆的初始化 (2)堆的销毁 (3)插入数据 …...
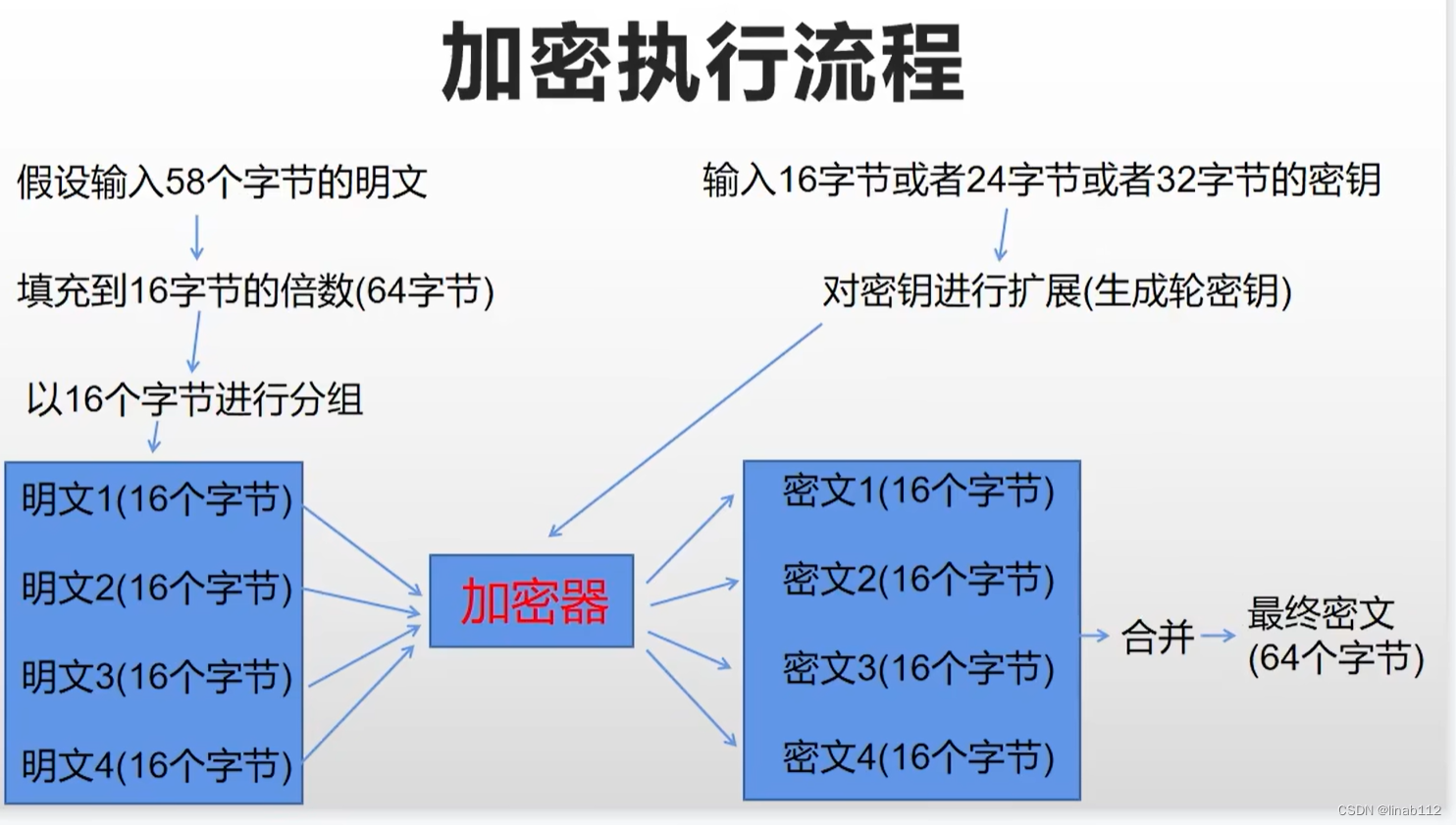
AES加密中的CBC和ECB
目录 1.说明 2.ECB模式(base64) 3.CBC模式 4.总结 1.说明 AES是常见的对称加密算法,加密和解密使用相同的密钥,流程如下: 主要概念如下: ①明文 ②密钥 用来加密明文的密码,在对称加密算…...

【C++】类和对象(四)
前言:在类和对象中,我们走过了十分漫长的道路,今天我们将进一步学习类和对象,类和对象这块荆棘地很长,各位一起加油呀。 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:高质量&a…...

XGB-5: DART Booster
XGBoost 主要结合了大量的回归树和一个小的学习率。在这种情况下,早期添加的树是重要的,而晚期添加的树是不重要的。 Vinayak 和 Gilad-Bachrach 提出了一种将深度神经网络社区的 dropout 技术应用于梯度提升树的新方法,并在某些情况下报告了…...
HiveSQL——不使用union all的情况下进行列转行
参考文章: HiveSql一天一个小技巧:如何不使用union all 进行列转行_不 union all-CSDN博客文章浏览阅读881次,点赞5次,收藏10次。本文给出一种不使用传统UNION ALL方法进行 行转列的方法,其中方法一采用了concat_wsposexplode()方…...
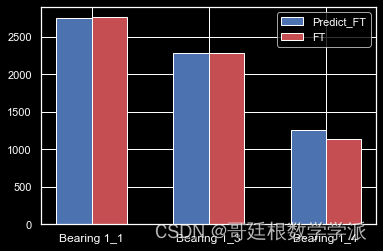
Python环境下基于指数退化模型和LSTM自编码器的轴承剩余寿命预测
滚动轴承是机械设备中关键的零部件之一,其可靠性直接影响了设备的性能,所以对滚动轴承的剩余使用寿命(RUL)进行预测是十分必要的。目前,如何准确地对滚动轴承剩余使用寿命进行预测,仍是一个具有挑战的课题。对滚动轴承剩余寿命评估…...
)
无人机竞赛视觉算法开发流程开源计划(询问大家意见)
本科中参加过一系列的无人机机器人竞赛,像电赛、工训赛、机器人大赛这些,有一些比较常用的方案打算开源一下。现在读研了,也算是对本科的一个总结,但是还是想看看大家意见,大家有什么需求可以在评论区说,我…...
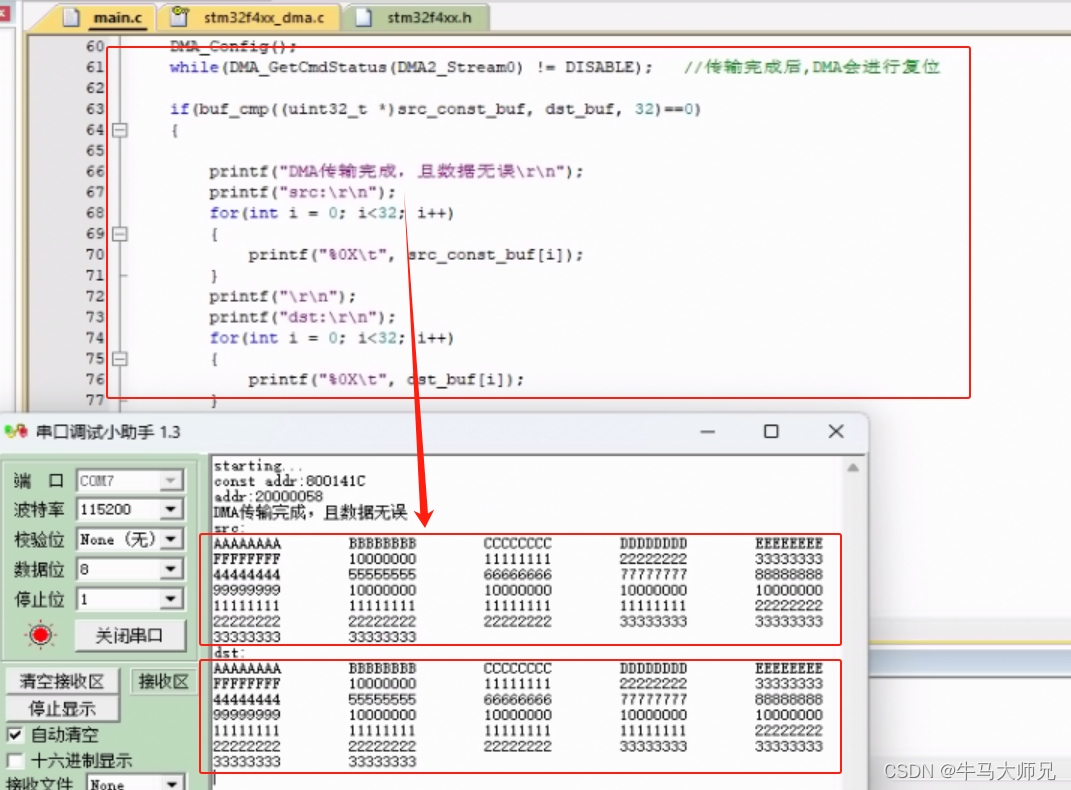
DMA直接内存访问,STM32实现高速数据传输使用配置
1、DMA运用场景 随着智能化、信息化的不断推进,嵌入式设备的数据处理量也呈现指数级增加,因此对于巨大的数据量处理的情况时,必须采取其它的方式去替CPU减负,以保证嵌入式设备性能。例如SD卡存储器和音视频、网络高速通信等其它情…...
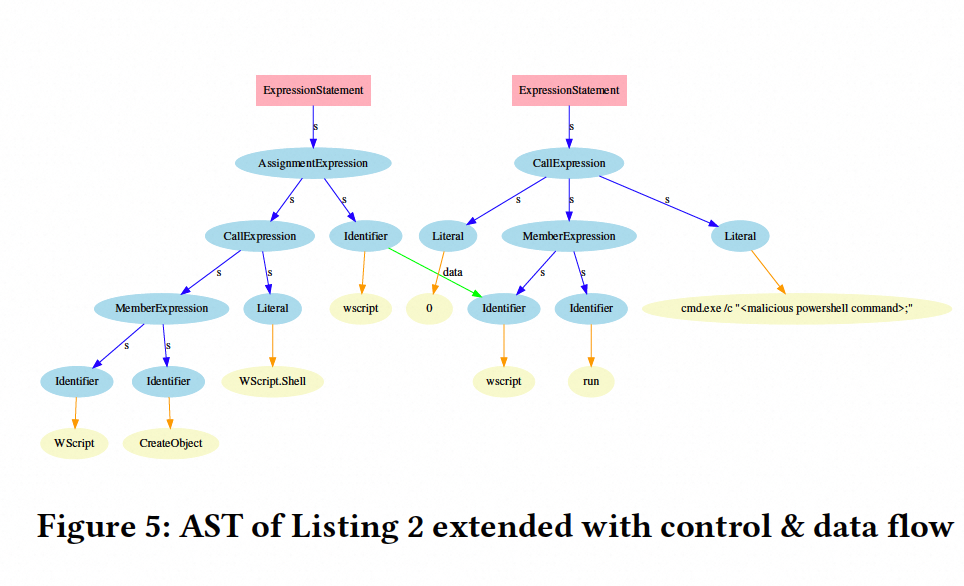
Web安全研究(六)
文章目录 HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs文章结构Introjs obfuscationmethodologyExample HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs CCS 2019 CISPA 恶意软件领域,基于学习的系统已经非常流行&am…...

python3 中try 异常调试 raise 异常抛出
一、什么是异常? 异常即是一个事件,该事件会在程序执行过程中发生,影响了程序的正常执行。 一般情况下,在Python无法正常处理程序时就会发生一个异常。 异常是Python对象,表示一个错误。 当Python脚本发生异常时我…...

Java中的序列化是什么?如何实现对象的序列化和反序列化?请解释Serializable接口的作用是什么?请解释transient关键字的作用是什么?为什么会使用它?
Java中的序列化是指将对象转换为字节序列的过程,以便可以在网络上传输或将其保存到持久存储介质中。反序列化则是将字节序列重新转换回对象的过程。Java提供了一种称为序列化(Serialization)的机制来实现对象的序列化和反序列化。 要实现对象…...

二维差分---三维差分算法笔记
文章目录 一.二维差分构造差分二维数组二维差分算法状态dp求b[i][j]数组的二维前缀和图解 二.三维前缀和与差分三维前缀和图解:三维差分核心公式图解:模板题 一.二维差分 给定一个原二维数组a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数…...

D. Divisible Pairs
思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。 代码: voi…...

【教程】Kotlin语言学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 文章目录 【Kotlin语言学习】系列文章一、基本数据…...

react 插槽
问题开发当中会经常出现组件十分相似的组件,只有一部分是不同的 解决: 父组件:在引用的时候 import { Component } from "react"; import Me from "../me";const name <div>名称</div> class Shoop extends Compone…...

Linux运用fork函数创建进程
fork函数: 函数原型: pid_t fork(void); 父进程调用fork函数创建一个子进程,子进程的用户区父进程的用户区完全一样,但是内核区不完全一样;如父进程的PID和子进程的PID不一样。 返回值: RETURN VALUEO…...

Pytest测试技巧之Fixture:模块化管理测试数据
在 Pytest 测试中,有效管理测试数据是提高测试质量和可维护性的关键。本文将深入探讨 Pytest 中的 Fixture,特别是如何利用 Fixture 实现测试数据的模块化管理,以提高测试用例的清晰度和可复用性。 什么是Fixture? 在 Pytest 中&a…...

设计模式-职责链模式Chain of Responsibility
职责链模式 一、原理和实现二、实现方式1) 使用链表实现2) 使用数组实现3) 扩展 作用:复用和扩展,在实际的项目开发中比较常用。在框架开发中,我们也可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下&…...

书生浦语大模型实战营-课程作业(3)
下载sentence_transformer的代码运行情况。sentence_transformer用于embedding(转向量) 本地构建持久化向量数据库。就是把txt和md文件抽取出纯文本,分割成定长(500)后转换成向量,保存到本地,称…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
