备战蓝桥杯---图论之最小生成树
首先,什么是最小生成树?
他就是无向图G中的所有生成树中树枝权值总和最小的。
如何求?
我们不妨采用以下的贪心策略:
Prim算法(复杂度:(n+m)logm):
我们对于把上述的点看成两个集合,一个是确定了最小生成树的点,一个还没有确定,我们只要不断把距离已经确定的集合的最短的边添加进去即可。假如我们加的距离不是最小的,那么当我们假设未确定的点已经构成了他们点的最小生成树,那么我们此时用距离最小的去添加他们肯定更优。(我们对于那先未确定的点的集合,不管用什么边去联系他们任何一个点,都不会影响他们以后的最小生成树的形状,这也是贪心当前最优解可以推出全局最优解的保证)
来道模板题:
因为传递消息,至少连n-1条边,又要距离min,相当于求最小生成树,下面是AC代码(我们可以优化一下,对于还未拿出的边,若有一个比他长的则不放入队列):
#include<bits/stdc++.h>
using namespace std;
int n,m,head[100010],a,b,v,cnt,sum;
struct node{int len,dian,next;
}edge[1000005];
void addedge(int x,int y,int v){edge[++cnt].len=v;edge[cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
int dis[100010];
struct ty{int bian,name;bool operator<(const ty &a) const{return bian>a.bian;}
};
bool vis[1000001];
priority_queue<ty> q;
int prim(){q.push({0,1});while(!q.empty()){ty ck=q.top();q.pop();if(vis[ck.name]==1) continue;vis[ck.name]=1;sum+=ck.bian;for(int i=head[ck.name];i!=-1;i=edge[i].next){if(vis[edge[i].dian]==1) continue;if(dis[edge[i].dian]<=edge[i].len) continue;dis[edge[i].dian]=edge[i].len;q.push({edge[i].len,edge[i].dian});}}return sum;
}
int main(){memset(head,-1,sizeof(head));memset(vis,0,sizeof(vis));memset(dis,0x3f,sizeof(dis));cin>>n>>m;for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&v);addedge(a,b,v);addedge(b,a,v);}cout<<prim();
}Kruskal算法(复杂度:mlogm):
还是采取贪心策略,只不过这次是直接选所有边下的最短边,若他们连起来还是树,就连起来,反之舍弃,用并查集维护即可。
首先,我们注意到如果每一次都可以选min的n-1条边就是最优的情况。
但是,在实际上,可能边会在同一个并查集中,说明这条边可以发挥构成树的作用,当时已经存在一点,他的作用是一样的,但是它的距离更小,因此更优。换句话说,我们就是在选n-1个在构建生成树的发挥不同作用的边,而之所以要放弃,是因为功能的重叠。
综上,这样选取的策略最优。
下面给出AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,fa[100010],a,b,v,cnt,sum;
struct node{int len,x,y;
}edge[1000005];
bool cmp(node a,node b){return a.len<b.len;
}
int find(int x){if(fa[x]==x) return x;else return fa[x]=find(fa[x]);
}
void merge(int x,int y){fa[find(x)]=find(y);
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&v);edge[++cnt].x=a;edge[cnt].y=b;edge[cnt].len=v;}sort(edge+1,edge+1+m,cmp);for(int i=1;i<=m;i++){int xx=find(edge[i].x);int yy=find(edge[i].y);if(xx==yy) continue;sum+=edge[i].len;merge(xx,yy);}cout<<sum;
}相关文章:

备战蓝桥杯---图论之最小生成树
首先,什么是最小生成树? 他就是无向图G中的所有生成树中树枝权值总和最小的。 如何求? 我们不妨采用以下的贪心策略: Prim算法(复杂度:(nm)logm): 我们对于把上述的点看成两个集…...
爬虫-华为云空间备忘录导出到docx-selenium控制浏览器行为-python数据处理
背景适用情况介绍 老的荣耀手机属于华为云系统,家里人换了新荣耀手机属于荣耀云系统无法通过云空间将备忘录转移到新手机,不想让他们一个一个搞,于是整了一晚上想办法爬取下来。从网页抓取下来,然后存到docx文档中(包…...

网络安全的新防线:主动进攻,预防为先
进攻性安全(Offensive security)是指一系列主动安全策略,这些策略与恶意行为者在现实世界的攻击中使用的策略相同,区别在于其目的是加强而非损害网络安全。常见的进攻性安全方法包括红队、渗透测试和漏洞评估。 进攻性安全行动通常…...
基于java springboot+mybatis学生学科竞赛管理管理系统设计和实现
基于java springbootmybatis学生学科竞赛管理管理系统设计和实现 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各…...
秒懂百科,C++如此简单丨第二十一天:栈和队列
目录 前言 Everyday English 栈(Stack) 图文解释 实现添加删除元素 实现查看清空栈 完整代码 运行示例 栈的选择题 队列(Queue) 图文解释 队列的基本用法 完整代码 运行结果 队列的好处 结尾 前言 今天我们将…...

STM32-开发环境之STM32CubeMX
目录 STM32CubeMX介绍 STM32CubeMX特性 应用场景 其他事项 STM32CubeMX介绍 STM32CubeMX是ST公司(意法半导体)推出的一款图形化工具,也是配置和初始化C代码生成器。它主要服务于STM32微控制器的配置和开发。 STM32CubeMX特性 1.直观选…...

[晓理紫]CCF系列会议截稿时间订阅
CCF系列会议截稿时间订阅 VX 关注{晓理紫},每日更新最新CCF系列会议信息,如感兴趣,请转发给有需要的同学,谢谢支持!! 如果你感觉对你有所帮助,请关注我,每日准时为你推送最新CCF会议…...
重复导航到当前位置引起的。Vue Router 提供了一种机制,阻止重复导航到相同的路由路径。
代码: <!-- 侧边栏 --><el-col :span"12" :style"{ width: 200px }"><el-menu default-active"first" class"el-menu-vertical-demo" select"handleMenuSelect"><el-menu-item index"…...

如何在 Angular 中使用 Flex 布局
介绍 Flex Layout 是一个组件引擎,允许您使用 CSS Flexbox 创建页面布局,并提供一组指令供您在模板中使用。 该库是用纯 TypeScript 编写的,因此不需要外部样式表。它还提供了一种在不同断点上指定不同指令以创建响应式布局的方法。 在本教…...

通俗的讲解什么是机器学习之损失函数
想象一下,你在玩一个靶心射击的游戏,你的目标是尽可能让箭簇命中靶心。在这个游戏中,损失函数可以看作是测量你的箭簇与靶心距离的规则。损失函数的值越小,意味着你的箭簇离靶心越近,你的射击技能越好。 在机器学习中…...
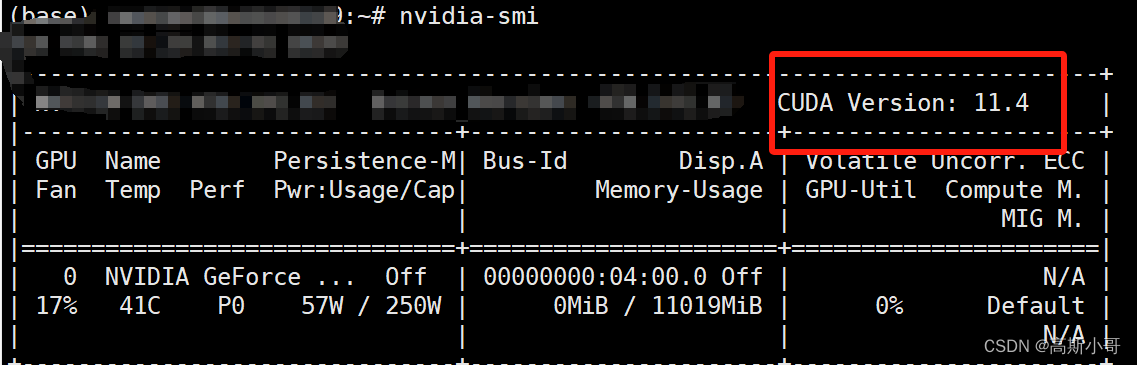
快速搭建PyTorch环境:Miniconda一步到位
快速搭建PyTorch环境:Miniconda一步到位 🌵文章目录🌵 🌳一、为何选择Miniconda搭建PyTorch环境?🌳🌳二、Miniconda安装指南:轻松上手🌳🌳三、PyTorch与Minic…...
图灵日记之java奇妙历险记--抽象类和接口
目录 抽象类概念抽象类语法 接口概念规则使用特性实现多个接口接口的继承接口使用实例Clonable接口和深拷贝抽象类和接口的区别 Object类 抽象类 概念 在面向对象的概念中,所有对象都是通过类来描述的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够…...

批量给元素添加进场动画;获取文本光标位置;项目国际化
批量给元素添加进场动画 api及参数参考:https://juejin.cn/post/7310977323484971071 简单实现: addAnimationClass(){//交叉观察器if (window?.IntersectionObserver) {//获取所有需要添加进场动画的元素,放到一个数组let items [...do…...
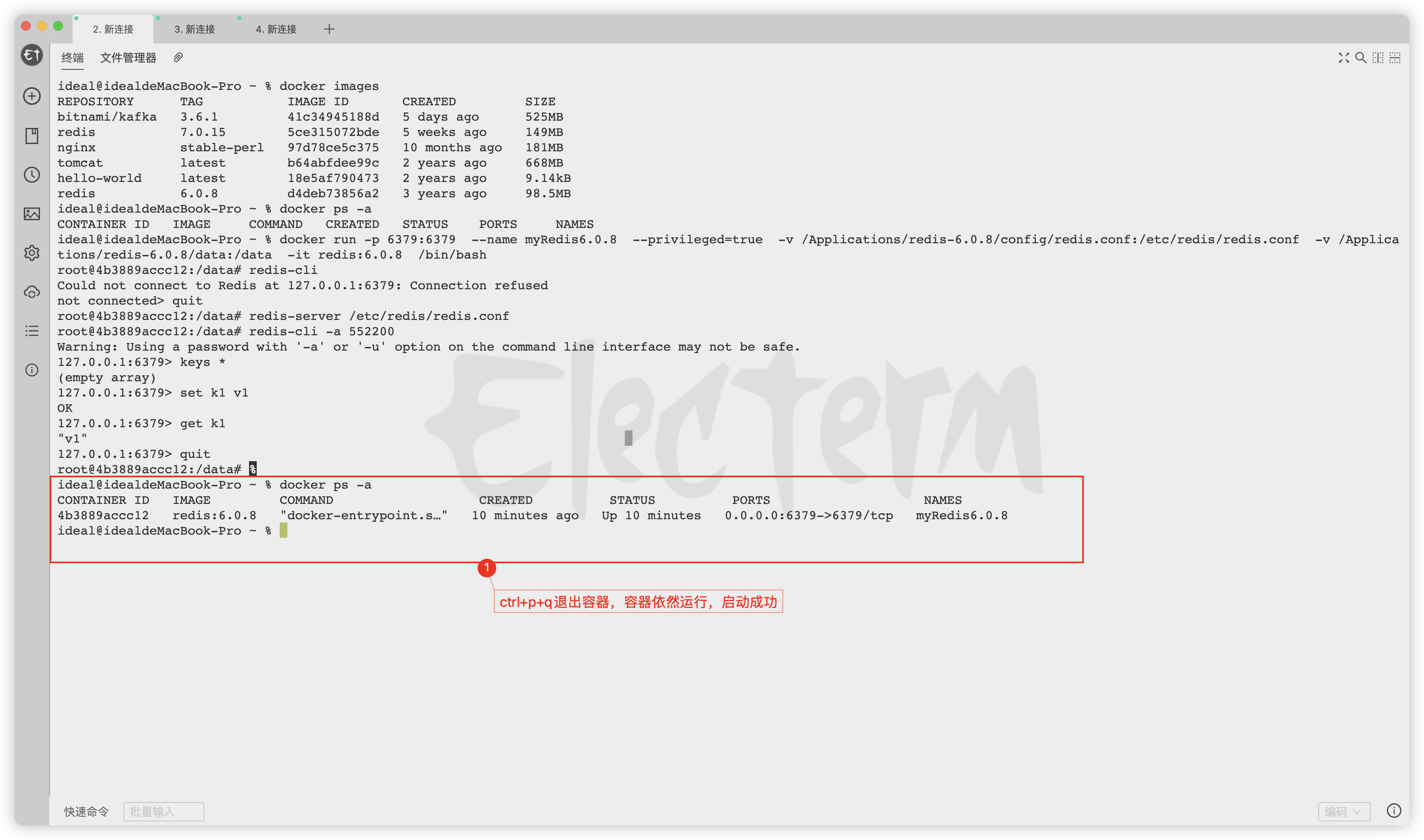
解决:docker创建Redis容器成功,但无法启动Redis容器、也无报错提示
解决:docker创建Redis容器成功,但无法启动Redis容器、也无报错提示 一问题描述:1.docker若是直接简单使用run命令,但不挂载容器数据卷等参数,则可以启动Redis容器2.docker复杂使用run命令,使用指定redis.co…...
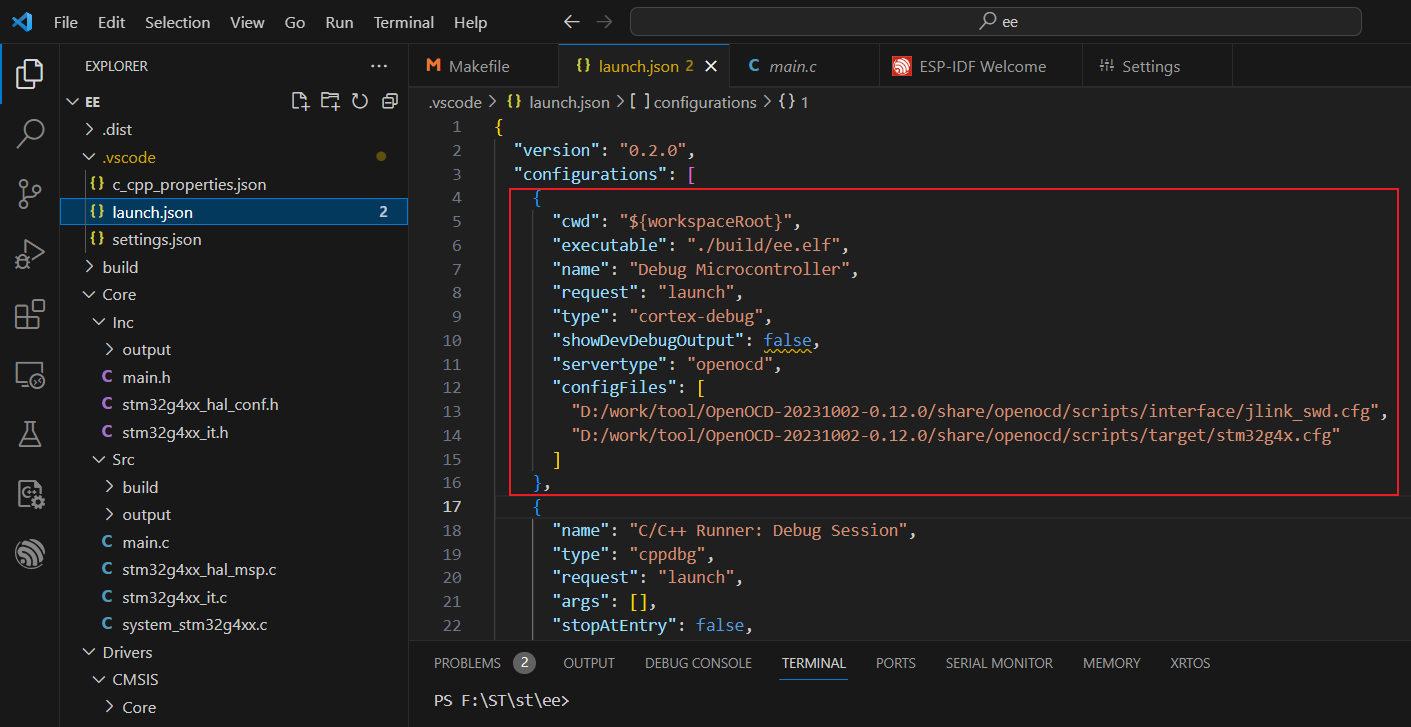
Jlink+OpenOCD+STM32 Vscode 下载和调试环境搭建
对于 Mingw 的安装比较困难,国内的网无法正常在线下载组件, 需要手动下载 x86_64-8.1.0-release-posix-seh-rt_v6-rev0.7z 版本的软件包,添加环境变量,并将 mingw32-make.exe 名字改成 make.exe。 对于 OpenOCD,需要…...

单片机在物联网中的应用
单片机,这个小巧的电子设备,可能听起来有点技术性,但它实际上是物联网世界中的一个超级英雄。简单来说,单片机就像是各种智能设备的大脑,它能让设备“思考”和“行动”。由于其体积小、成本低、功耗低、易于编程等特点…...
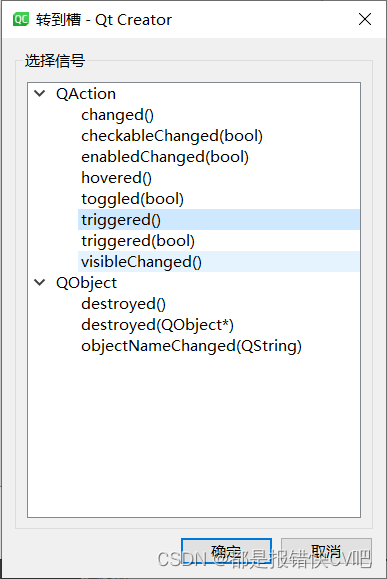
16.Qt 工具栏生成
目录 前言: 技能: 内容: 1. 界面添加 2. 信号槽 功能实现 参考: 前言: 基于QMainWindow,生成菜单下面的工具栏,可以当作菜单功能的快捷键,也可以完成新的功能 直接在UI文件中…...
【Linux内核】从0开始入门Linux Kernel源码
🌈 博客个人主页:Chris在Coding 🎥 本文所属专栏:[Linux内核] ❤️ 前置学习专栏:[Linux学习]从0到1 ⏰ 我们仍在旅途 目录 …...
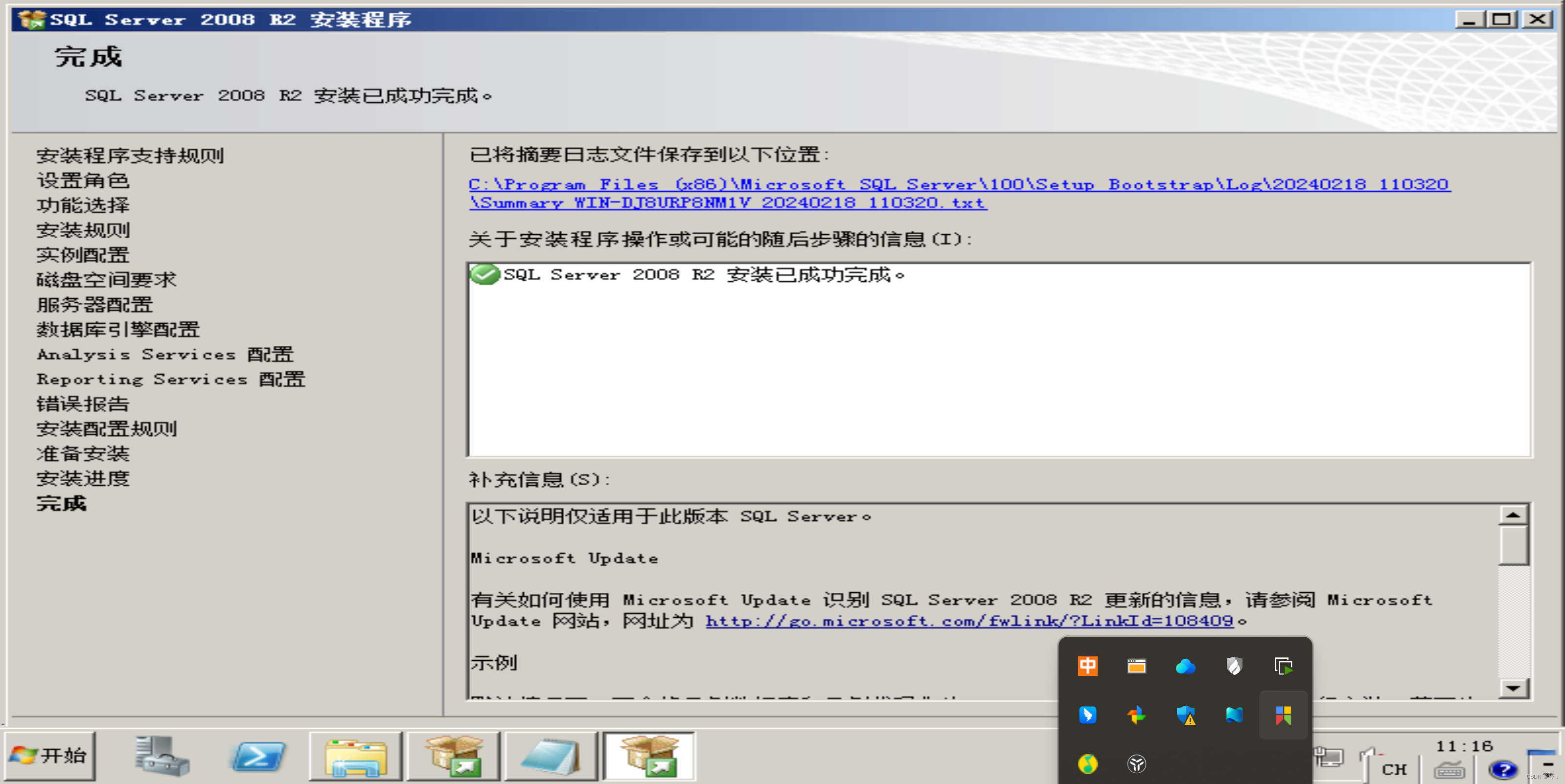
SQL Service 2008 的安装与配置
点击添加当前用户...
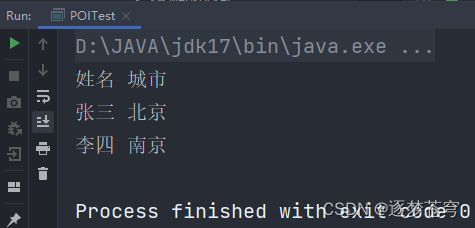
Apache POI | Java操作Excel文件
目录 1、介绍 2、代码示例 2.1、将数据写入Excel文件 2.2、读取Excel文件中的数据 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
