(AtCoder Beginner Contest 341)(A - D)
比赛地址 :
Tasks - Toyota Programming Contest 2024#2(AtCoder Beginner Contest 341)
A . Print 341
模拟就好了 , 先放一个 1 , 然后放 n 个 01 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;using namespace std;inline void solve(){int n ; cin >> n ;cout << 1 ;for(int i=0;i<n;i++){cout << "01";}
}signed main()
{IOSint _ = 1;// cin >> _;while(_ --) solve();return 0;
}B . Foreign Exchange
贪心, 因为后面操作不会影响前面的,前面的会使后面的变大,而题目要求使最后一个最大,那么 , 直接从前往后遍历就好了 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;using namespace std;inline void solve() {int n ; cin >> n ;vector<int> a(n+1) ,s(n) , t(n) ;for(int i=1;i<=n;i++) cin >> a[i] ;for(int i=1;i<n;i++) cin >> s[i] >> t[i] ;// 第i个-si ,i+1就+tifor(int i=1;i<n;i++){if(a[i] >= s[i]){int k = a[i] / s[i] ;a[i] -= k * s[i] ;a[i+1] += k * t[i] ; }}cout << a[n] << endl;
} signed main()
{IOSint _ = 1;// cin >> _;while (_--) solve();return 0;
}C . TaKahashi Gets Lost
暴力 , 对于每一个点,找它是否满足题意,如果满足,则ans++;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 510;char c[N][N] ;using namespace std;inline void solve(){int h,w,n;cin>>h>>w>>n ;string t ; cin >> t ;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){cin >> c[i][j] ;}}int ans = 0 ;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){if(c[i][j]=='#') continue ;int a = i , b = j ;bool tag = true;for(int k=0;k<n;k++){if(t[k]=='L'){if(b==1){tag = false;break ; }b-=1;if(c[a][b]=='#'){tag = false;break;}}else if(t[k]=='U'){if(a==1){tag = false;break ; }a-=1;if(c[a][b]=='#'){tag = false;break;}}else if(t[k]=='R'){if(b==w){tag = false;break ; }b+=1;if(c[a][b]=='#'){tag = false;break;}}else{// "D"if(a==h){tag = false;break ; }a+=1;if(c[a][b]=='#'){tag = false;break;}}}if(tag){ans ++ ;}}}cout << ans << endl ;
}signed main()
{IOSint _ = 1;// cin >> _;while(_ --) solve();return 0;
}D . Only one of two
先找到n,m的最小公倍数l,那么对于一个数x,能被n整除且<=x的数的个数就是[x/n],所以可以得到下面式子(因为可能同时能被n,m整除,要删掉能被l整除的数字个数):
[x/n] + [x/m] - 2 * [x/l] >= k;
这样就可以使用二分来进行查找 ;
#include <bits/stdc++.h>
using namespace std;
typedef long long LL ;
LL gcd(LL a , LL b){return b ? gcd(b, a % b) : a;
}// 设 l 是 m,n的最小公倍数 int main() {long long n,m,x,k;cin>>n>>m>>k;x=(n*m)/gcd(n,m);// 求出最小公倍数 long long l=0,r=(long long)2e+18,mid,y;while((l+1)<r){// 二分查找 t/n+t/m-2*t/x>=k的最佳答案 mid=(l+r)/2;y=(mid/n)+(mid/m)-2*(mid/x);if(y<k)l=mid;else r=mid;}cout<<r<<endl;return 0;
}
相关文章:

(AtCoder Beginner Contest 341)(A - D)
比赛地址 : Tasks - Toyota Programming Contest 2024#2(AtCoder Beginner Contest 341) A . Print 341 模拟就好了 , 先放一个 1 , 然后放 n 个 01 ; #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout…...

python Flask与微信小程序 统计管理
common/models/stat/StatDailyMember.py DROP TABLE IF EXISTS stat_daily_member;CREATE TABLE stat_daily_member (id int(11) unsigned NOT NULL AUTO_INCREMENT,date date NOT NULL COMMENT 日期,member_id int(11) NOT NULL DEFAULT 0 COMMENT 会员id,total_shared_count …...

光伏企业助力乡村振兴
光伏是一种利用太阳能生产电能的发电技术,属于可再生能源。近年来我国的光伏企业发展迅速,已经称霸全球,同时也为乡村振兴贡献了力量。 一、光伏企业助力乡村 1.推动农业发展 光伏发电和农业种植、畜牧、渔业、水产等有机结合,…...

root MUSIC 算法补充说明
root MUSIC 算法补充说明 多项式求根root MUSIC 算法原理如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根从复数域上观察 2 M − 2 2M-2 2M−2 个根的分布 这篇笔记是上一篇关于 root MUSIC 笔记的补充。 多项式求根 要理解 root MUSIC 算法,需要理解多项式求…...

关于Django的中间件使用说明。
目录 1.中间件2. 为什么要中间件?3. 具体使用中间件3.1 中间件所在的位置:在django的settings.py里面的MIDDLEWARE。3.2 中间件的创建3.3 中间件的使用 4. 展示成果 1.中间件 中间件的大概解释:在浏览器在请求服务器的时候,首先要…...

Chapter 8 - 15. Congestion Management in TCP Storage Networks
User Actions After learning the states of queue utilization, the following are the actions that admins and operators can take while using TCP transport for storage traffic. 了解了队列利用率的状态后,管理员和操作员在使用 TCP 传输存储流量时可以采取以下措施。…...

前端技巧之svg精灵图svg-sprite-loader
首先说明精灵图的必要性,其可以让我们只需要向服务器请求一次图片资源,就能加载很多图片,即能够减轻http请求造成的服务器压力。 然后这里要说明的是这个插件是webpack上面的,所以在vue2中比较好用,如果在vue3中&…...

IO线程-day2
1> 使用fread和fwrite完成两个文件的拷贝 程序: #define MAXSIZE 1024 #include<myhead.h>int main(int argc, char const *argv[]) {FILE *srcfpNULL;FILE *destfpNULL;if(!(srcfpfopen("pm.bmp","r")))PRINT_ERR("");if…...
Spring Boot 笔记 024 登录页面
1.1 登录接口 //导入request.js请求工具 import request from /utils/request.js//提供调用注册接口的函数 export const userRegisterService (registerData)>{//借助于UrlSearchParams完成传递const params new URLSearchParams()for(let key in registerData){params.a…...

09_Java集合
一、Java集合框架概述 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态…...

HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-软件定时器
目录 一、软件定时器基本概念二、软件定时器运行机制三、软件定时器状态四、软件定时器模式五、软件定时器开发流程六、软件定时器使用说明七、软件定时器接口八、代码分析(待续...)坚持就有收获 一、软件定时器基本概念 软件定时器,是基于系…...
考研证件照可以自己用手机拍吗?考研证件照p过可以通过审核吗?考研证件照有什么要求
一、考研证件照可以自己用手机拍吗 现在的智能手机相机技术先进,大多都配备了高像素摄像头,使得自拍照片的质量有了大幅提升。相较于传统的证件照拍摄,使用手机自拍考研证件照理论上是可行的。然而,考研证件照需要满足一定的规定…...
win10 环境下Python 3.8按装fastapi paddlepaddle 进行图片文字识别1
###按装 用conda 创建python 3.8的环境,可参看本人python下的其它文章。 在pycharm开发环境下按装相关的模块: pip install -i https://pypi.tuna.tsinghua.edu.cn/simple fastapi pip install -i https://pypi.tuna.tsinghua.edu.cn/simple "uvi…...

json字符串的处理
json字符串的处理 【1】解析json字符串(1)如果json格式字符串 ,最外层 是 中括号,表示数组,就使用方法(2)如果json格式字符串,最外层是 大括号,表示对象,就是…...

Java基础String常见的编程练习
1.对字符串数组进行排序 package javalianxi;import java.util.Arrays; import java.util.Comparator;public class Test1 {public static void main(String[] args) {String[] array { "cd", "CD", "bc", "AB", "ab", &q…...
| 491.递增子序列 46.全排列 47.全排列 II)
代码随想录算法训练营(回溯5)| 491.递增子序列 46.全排列 47.全排列 II
491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 题目链接/文章讲解 视频讲解 46.全排列 本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用…...

专业140+总分420+南京信息工程大学811信号与系统考研经验南信大电子信息与通信工程,真题,大纲,参考书
今年顺利被南信大电子信息录取,初试420,专业811信号与系统140(Jenny老师辅导班上140很多,真是大佬云集),今年应该是南信大电子信息最卷的一年,复试线比往年提高了很多,录取平均分380…...

一元函数微分学【高数笔记】
1. 什么是微分?什么是微商? 2. 什么是函数的微分? 3. 在函数的微分中,有什么样的关系? 4. 一元函数的微分运用在什么题型中? 5. 什么是一元函数?...
(16)Hive——企业调优经验
前言 本篇文章主要整理hive-3.1.2版本的企业调优经验,有误请指出~ 一、性能评估和优化 1.1 Explain查询计划 使用explain命令可以分析查询计划,查看计划中的资源消耗情况,定位潜在的性能问题,并进行相应的优化。 explain执行计划…...
【详解】图的概念和存储结构(邻接矩阵,邻接表)
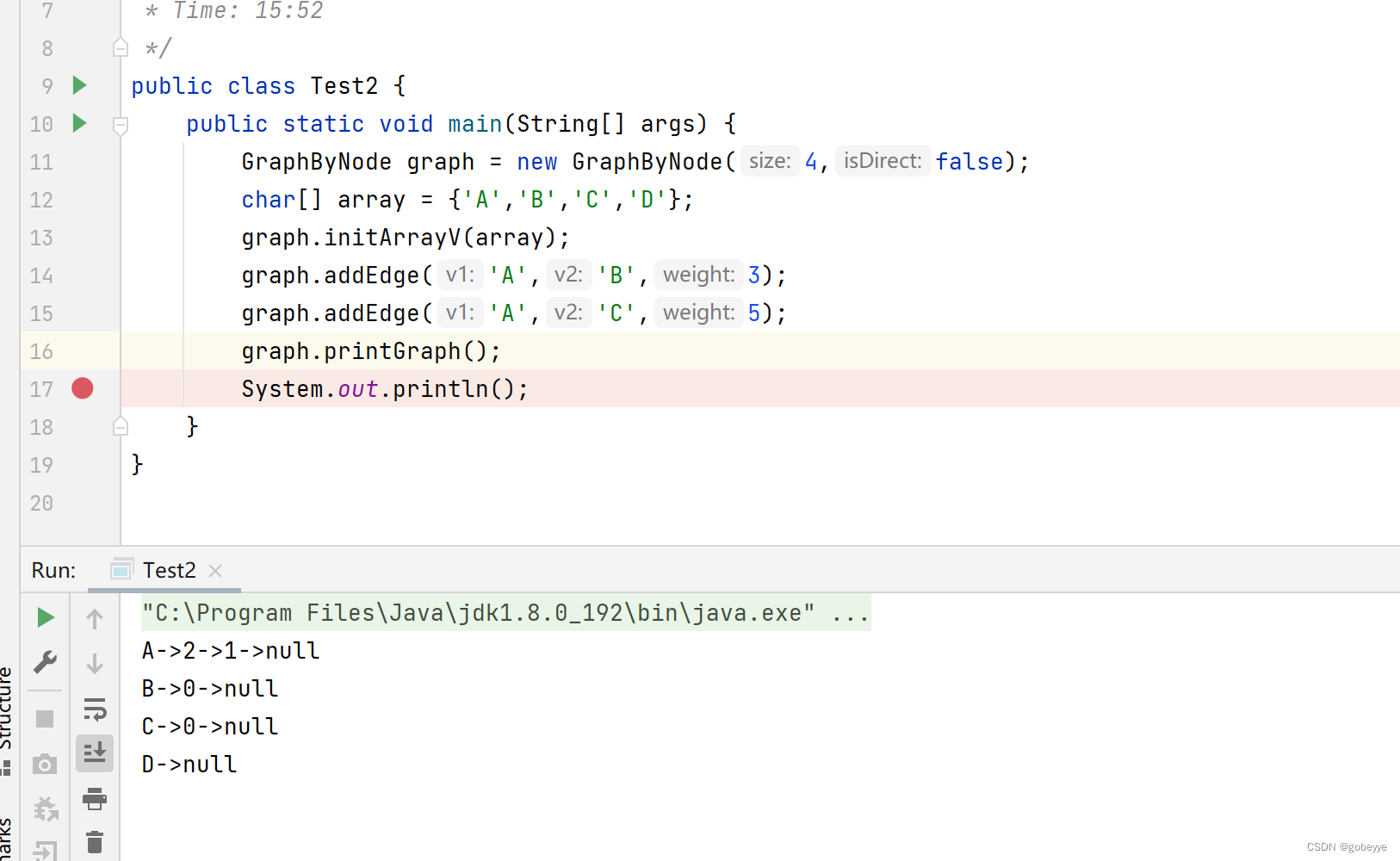
目录 图的基本概念: 图的存储结构 邻接矩阵(GraphByMatrix): 基本参数: 初始化: 获取顶点元素在其数组中的下标 : 添加边和权重: 获取顶点的度: 打印图…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
