root MUSIC 算法补充说明
root MUSIC 算法补充说明
- 多项式求根
- root MUSIC 算法原理
- 如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根
- 从复数域上观察 2 M − 2 2M-2 2M−2 个根的分布
这篇笔记是上一篇关于 root MUSIC 笔记的补充。
多项式求根
要理解 root MUSIC 算法,需要理解多项式求根的相关知识。给定多项式 P ( x ) P(x) P(x):
P ( x ) = a 0 + a 1 x + ⋯ + a n x n P(x) = a_0 + a_1 x + \cdots + a_n x^n P(x)=a0+a1x+⋯+anxn
容易看出 P ( x ) P(x) P(x) 中只有一个未知数 x x x,且未知数的最高次数为 n n n,因此称 P ( x ) P(x) P(x) 为一元 n n n 次多项式,同时系数 { a i ∈ C : i = 0 , ⋯ , n } \{a_i\in\mathbb{C}:i = 0,\cdots, n\} {ai∈C:i=0,⋯,n}。而多项式求根就是求得一元 n n n 次方程式 P ( x ) = 0 P(x)=0 P(x)=0 的解,这个解被称作根或者零点。
在进行后续的讨论前,还需要清楚,根据代数基本定理, n n n 次复系数多项式方程在复数域内有且只有 n n n 个根(这里的重根按重数计算)。
root MUSIC 算法原理
root MUSIC 算法是 MUSIC 算法的一种多项式求根形式。回忆一下,传统 MUSIC 算法利用了噪声子空间矩阵 U n \mathbf{U}_n Un 和搜索方向矢量 a ( θ ) \mathbf{a}(\theta) a(θ) 来构造空间谱:
P ( θ ) = 1 a H ( θ ) U n U n H a ( θ ) a ( θ ) = [ 1 , e − j 2 π d sin θ / λ , ⋯ , e − j 2 π ( M − 1 ) d sin θ / λ ] T P(\theta) = \frac{1}{\mathbf{a}^H(\theta)\mathbf{U}_n\mathbf{U}^H_n\mathbf{a}(\theta)} \\ \mathbf{a}(\theta) = \left[1,e^{-\mathrm{j}2\pi d \sin \theta/\lambda},\cdots,e^{-\mathrm{j}2\pi(M-1) d \sin \theta/\lambda}\right]^T P(θ)=aH(θ)UnUnHa(θ)1a(θ)=[1,e−j2πdsinθ/λ,⋯,e−j2π(M−1)dsinθ/λ]T
在 { θ = θ k : k = 1 , ⋯ , K } \{\theta = \theta_k:k = 1,\cdots,K\} {θ=θk:k=1,⋯,K} 时 P ( θ ) P(\theta) P(θ) 将产生峰值,换句话说此时 P − 1 ( θ ) = 0 P^{-1}(\theta)=0 P−1(θ)=0。
在接下来的讨论中,我们令 P − 1 ( θ ) = a H ( θ ) G a ( θ ) P^{-1}(\theta) = \mathbf{a}^H(\theta)\mathbf{G}\mathbf{a}(\theta) P−1(θ)=aH(θ)Ga(θ),此时我们可以知道,MUSIC 算法满足 G ≜ U n U n H \mathbf{G} \triangleq \mathbf{U}_n\mathbf{U}^H_n G≜UnUnH,而 Capon 算法满足 G ≜ R − 1 \mathbf{G} \triangleq \mathbf{R}^{-1} G≜R−1。需要注意的是无论是 MUSIC 算法还是 Capon 算法, G \mathbf{G} G 均是 Hermitian 矩阵。
令 ω = − 2 π d sin θ / λ \omega = -2\pi d \sin\theta/\lambda ω=−2πdsinθ/λ 以及 z = e j ω z = e^{\mathrm{j}\omega} z=ejω,我们将会得到:
a ( z ) = [ 1 , z , z 2 , ⋯ , z M − 1 ] T = a ( θ ) P − 1 ( z ) = a H ( z ) G a ( z ) = P − 1 ( θ ) \begin{aligned} \mathbf{a}(z) &= [1,z,z^{2},\cdots,z^{M-1}]^T = \mathbf{a}(\theta) \\ P^{-1}(z) &= \mathbf{a}^H(z)\mathbf{G}\mathbf{a}(z) = P^{-1}(\theta) \end{aligned} a(z)P−1(z)=[1,z,z2,⋯,zM−1]T=a(θ)=aH(z)Ga(z)=P−1(θ)
接下来我们展开 P − 1 ( z ) P^{-1}(z) P−1(z):
P − 1 ( z ) = a H ( z ) G a ( z ) = [ 1 , z ∗ , ( z ∗ ) 2 , ⋯ , ( z ∗ ) M − 1 ] G [ 1 , z , z 2 , ⋯ , z M − 1 ] T = [ 1 , z − 1 , z − 2 , ⋯ , z − M + 1 ] G [ 1 , z , z 2 , ⋯ , z M − 1 ] T = ∑ m = 0 M − 1 ∑ n = 0 M − 1 z − m G [ m , n ] z n = ∑ m = 0 M − 1 ∑ n = 0 M − 1 z n − m G [ m , n ] = ∑ p = − M + 1 M − 1 a p z − p \begin{aligned} P^{-1}(z) &= \mathbf{a}^H(z)\mathbf{G}\mathbf{a}(z) \\ &= [1,z^{*},(z^{*})^2,\cdots,(z^*)^{M-1}] \mathbf{G} [1,z,z^{2},\cdots,z^{M-1}]^T \\ &= [1,z^{-1},z^{-2},\cdots,z^{-M+1}] \mathbf{G} [1,z,z^{2},\cdots,z^{M-1}]^T \\ &= \sum_{m = 0}^{M-1} \sum_{n=0}^{M-1} z^{-m} \mathbf{G}_{[m,n]} z^{n} \\ &= \sum_{m = 0}^{M-1} \sum_{n=0}^{M-1} z^{n-m} \mathbf{G}_{[m,n]} \\ &=\sum_{p=-M+1}^{M-1}a_p z^{-p} \end{aligned} P−1(z)=aH(z)Ga(z)=[1,z∗,(z∗)2,⋯,(z∗)M−1]G[1,z,z2,⋯,zM−1]T=[1,z−1,z−2,⋯,z−M+1]G[1,z,z2,⋯,zM−1]T=m=0∑M−1n=0∑M−1z−mG[m,n]zn=m=0∑M−1n=0∑M−1zn−mG[m,n]=p=−M+1∑M−1apz−p
其中 G [ m , n ] \mathbf{G}_{[m,n]} G[m,n] 表示矩阵 G \mathbf{G} G 的第 m m m 行第 n n n 列元素, a p a_p ap 表示矩阵 G \mathbf{G} G 的第 p p p 条对角线的求和:
a p ≜ ∑ m − n = p G [ m , n ] a_p \triangleq \sum_{m-n = p} \mathbf{G}_{[m,n]} ap≜m−n=p∑G[m,n]
到这里我们已经可以看出,传统 MUSIC 算法对 P ( θ ) P(\theta) P(θ) 求峰值,其实等价于对 P − 1 ( z ) P^{-1}(z) P−1(z) 求根,为了方便大家的理解,我们令 M = 3 M=3 M=3,此时会得到一条简单的式子:
P − 1 ( z ) = a 2 z − 2 + a 1 z − 1 + a 0 z 0 + a − 1 z 1 + a − 2 z 2 P^{-1}(z) = a_{2}z^{-2}+a_{1}z^{-1} + a_{0}z^{0} + a_{-1}z^{1} + a_{-2}z^{2} P−1(z)=a2z−2+a1z−1+a0z0+a−1z1+a−2z2
可以看出,其实 P − 1 ( θ ) P^{-1}(\theta) P−1(θ) 是一个 2 M − 1 = 5 2M-1 = 5 2M−1=5 项的多项式,但还存在一个问题, P − 1 ( θ ) P^{-1}(\theta) P−1(θ) 中存在负整数次数,我们令 P − 1 ( z ) z M − 1 P^{-1}(z)z^{M-1} P−1(z)zM−1 将负整数次数消除即可,操作前后,求根的结果是一样的,因此我们可以说 P − 1 ( z ) z M − 1 P^{-1}(z)z^{M-1} P−1(z)zM−1 是一个一元的 2 M − 1 2M-1 2M−1 项的 2 M − 2 2M-2 2M−2 次的多项式。更进一步地,我们可以说求解 P − 1 ( z ) z M − 1 = 0 P^{-1}(z)z^{M-1}=0 P−1(z)zM−1=0 将会得到 2 M − 2 2M-2 2M−2 个根,从已知条件我们知道,其中 K K K 个根必定是 e j ω k e^{\mathrm{j}\omega_k} ejωk( e j ω k e^{\mathrm{j}\omega_k} ejωk 的幅值是 1 1 1,因此该 K K K 点在单位圆上),在这里 ω k = − 2 π d sin θ k / λ \omega_k = -2\pi d \sin\theta_k/\lambda ωk=−2πdsinθk/λ。
总结一下,MUSIC 算法的谱峰搜索操作等价于对方程式 P − 1 ( z ) z M − 1 = 0 P^{-1}(z)z^{M-1}=0 P−1(z)zM−1=0 求根,root MUSIC 算法所做的,就是利用 G \mathbf{G} G 的多条对角线求和得到对应的多项式系数,从而求解得 2 M − 2 2M-2 2M−2 个根,接着筛选得到合适的 K K K 个根 z k z_k zk,再通过 z k z_k zk 推导得到原先的 θ k \theta_k θk。
如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根
那么如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根?这个问题大部分的论文和博客都一笔带过了。从前面的讨论可知,多项式系数是由 G \mathbf{G} G 的多条对角线求和得到,同时 G \mathbf{G} G 是 Hermitian 矩阵,因此以下式子可以得到:
a p = a − p ∗ a_p = a_{-p}^* ap=a−p∗
这个等式意味着在 2 M − 1 2M-1 2M−1 个系数 { a p : p = − M + 1 , ⋯ , M − 1 } \{a_p:p=-M+1,\cdots,M-1\} {ap:p=−M+1,⋯,M−1} 中,前 M − 1 M-1 M−1 个和后 M − 1 M-1 M−1 个系数是前后共轭对称,同时正中间的系数是实数。
我们继续假设 M = 3 M=3 M=3, P − 1 ( z ) = 0 P^{-1}(z)=0 P−1(z)=0 可以进一步表示如下:
P − 1 ( z ) = a 2 z − 2 + a 1 z − 1 + a 0 + a 1 ∗ z 1 + a 2 ∗ z 2 = 0 P^{-1}(z) = a_{2}z^{-2}+a_{1}z^{-1} + a_{0} + a_{1}^*z^{1} + a_{2}^*z^{2}=0 P−1(z)=a2z−2+a1z−1+a0+a1∗z1+a2∗z2=0
如此我们分析 P − 1 ( 1 / z ∗ ) P^{-1}(1/z^*) P−1(1/z∗),可得:
P − 1 ( 1 / z ∗ ) = a 2 ( z ∗ ) 2 + a 1 ( z ∗ ) 1 + a 0 + a 1 ∗ ( z ∗ ) − 1 + a 2 ∗ ( z ∗ ) − 2 = [ P − 1 ( z ) ] ∗ = P − 1 ( z ) = 0 \begin{aligned} P^{-1}(1/z^*) &= a_{2}(z^*)^{2}+a_{1}(z^*)^{1} + a_{0} + a_{1}^*(z^*)^{-1} + a_{2}^*(z^*)^{-2} \\ &=[P^{-1}(z)]^* = P^{-1}(z) = 0 \end{aligned} P−1(1/z∗)=a2(z∗)2+a1(z∗)1+a0+a1∗(z∗)−1+a2∗(z∗)−2=[P−1(z)]∗=P−1(z)=0
这意味着假若 z 1 = ρ e j φ z_1 = \rho e^{\mathrm{j}\varphi} z1=ρejφ 是 P − 1 ( z ) = 0 P^{-1}(z)=0 P−1(z)=0 的根,那么 z 2 = 1 / z 1 ∗ = 1 / ρ e j φ z_2 = 1/z_1^* = 1/\rho e^{\mathrm{j}\varphi} z2=1/z1∗=1/ρejφ 同样是 P − 1 ( z ) = 0 P^{-1}(z)=0 P−1(z)=0 的根。观察 z 1 z_1 z1 和 z 2 z_2 z2 在复平面的位置,将会观察得到 z 1 z_1 z1 和 z 2 z_2 z2 是关于单位圆有一个类似对称的关系;简单来说,这个现象是因为 z 1 z_1 z1 和 z 2 z_2 z2 是幅值互为倒数而相位相等的关系,因此它们就像是关于 e j φ e^{\mathrm{j}\varphi} ejφ 对称一样( e j φ e^{\mathrm{j}\varphi} ejφ 的幅值是 1 1 1,因此该点在单位圆上)。
综上所述,通过 P − 1 ( z ) P^{-1}(z) P−1(z) 得到 2 M − 2 2M-2 2M−2 个根,它们是关于单位圆对称的 M − 1 M-1 M−1 对根,因此一定有 K K K 对根在单位圆附近,所以我们只需要从 2 M − 2 2M-2 2M−2 个根中找 M − 1 M-1 M−1 个处于单位圆内的根(找 M − 1 M-1 M−1 个处于单位圆外的根同样是可以的,因为角度信息其实只存在于 z k z_k zk 的相位中,与幅值无关),最后确定最接近单位圆的 K K K 个根就可以确定 z k z_k zk。
从复数域上观察 2 M − 2 2M-2 2M−2 个根的分布
我们从实验中进一步观察 2 M − 2 2M-2 2M−2 个根的分布,matlab 代码实现如下:
clear; close all; clc;%% Parameters
lambda = 3e8/1e9; % wavelength, c/f
d = lambda/4; % distance between sensors
theta = [10,20]; % true DoAs, 1 times K vector
theta = sort(theta);
M = 16; % # of sensors
T = 500; % # of snapshots
K = length(theta); % # of signals
noise_flag = 1;
SNR = 0; % signal-to-noise ratio%% Signals
S = exp(1j*2*pi*randn(K,T)); % signal matrix
A = exp(-1j*(0:M-1)'*2*pi*d/lambda*sind(theta)); % steering vector matrix
N = noise_flag.*sqrt(10.^(-SNR/10))*(1/sqrt(2))*(randn(M,T)+1j*randn(M,T)); % noise matrix
X = A*S+N; % received matrix
R = X*X'/T; % covariance matrix%% DoA:root-MUSIC
[U,~] = svd(R); % SVD
Un = U(:, K+1:end); % noise subspace matrix
Gn = Un*Un';
coe = arrayfun(@(i) sum(diag(Gn, M-i)),(1:2*M-1));
r = roots(coe); % 2M-2 roots%% plot
dis = sort(abs(r)-1);
disp(dis);
cnt = sum(dis<0);
disp(cnt); % 记录单位圆内的根个数% 提取实部和虚部
realPart = real(r);
imaginaryPart = imag(r);% 绘制复平面
figure;
scatter(realPart, imaginaryPart, 'filled');
hold on;% 绘制单位圆
theta = linspace(0, 2*pi, 100);
unitCircleReal = cos(theta);
unitCircleImag = sin(theta);
plot(unitCircleReal, unitCircleImag, 'r--', 'LineWidth', 1);xlabel('实部');
ylabel('虚部');
title('复平面上的复数点和单位圆');
grid on;
box on;%% find K roots
r = r(abs(r)<1);
[~, idx] = sort(abs(abs(r)-1));
z = angle(r(idx));
theta = sort(asin(-z(1:K)/2/pi/d*lambda)/pi*180).';
设 M = 16 M=16 M=16 和 K = 2 K=2 K=2,根的分布如下图所示,可以看到 2 M − 2 = 30 2M-2 = 30 2M−2=30 个根,其中 2 K = 4 2K=4 2K=4 个接近单位圆的根对应着估计角度:

相关文章:

root MUSIC 算法补充说明
root MUSIC 算法补充说明 多项式求根root MUSIC 算法原理如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根从复数域上观察 2 M − 2 2M-2 2M−2 个根的分布 这篇笔记是上一篇关于 root MUSIC 笔记的补充。 多项式求根 要理解 root MUSIC 算法,需要理解多项式求…...

关于Django的中间件使用说明。
目录 1.中间件2. 为什么要中间件?3. 具体使用中间件3.1 中间件所在的位置:在django的settings.py里面的MIDDLEWARE。3.2 中间件的创建3.3 中间件的使用 4. 展示成果 1.中间件 中间件的大概解释:在浏览器在请求服务器的时候,首先要…...

Chapter 8 - 15. Congestion Management in TCP Storage Networks
User Actions After learning the states of queue utilization, the following are the actions that admins and operators can take while using TCP transport for storage traffic. 了解了队列利用率的状态后,管理员和操作员在使用 TCP 传输存储流量时可以采取以下措施。…...

前端技巧之svg精灵图svg-sprite-loader
首先说明精灵图的必要性,其可以让我们只需要向服务器请求一次图片资源,就能加载很多图片,即能够减轻http请求造成的服务器压力。 然后这里要说明的是这个插件是webpack上面的,所以在vue2中比较好用,如果在vue3中&…...

IO线程-day2
1> 使用fread和fwrite完成两个文件的拷贝 程序: #define MAXSIZE 1024 #include<myhead.h>int main(int argc, char const *argv[]) {FILE *srcfpNULL;FILE *destfpNULL;if(!(srcfpfopen("pm.bmp","r")))PRINT_ERR("");if…...
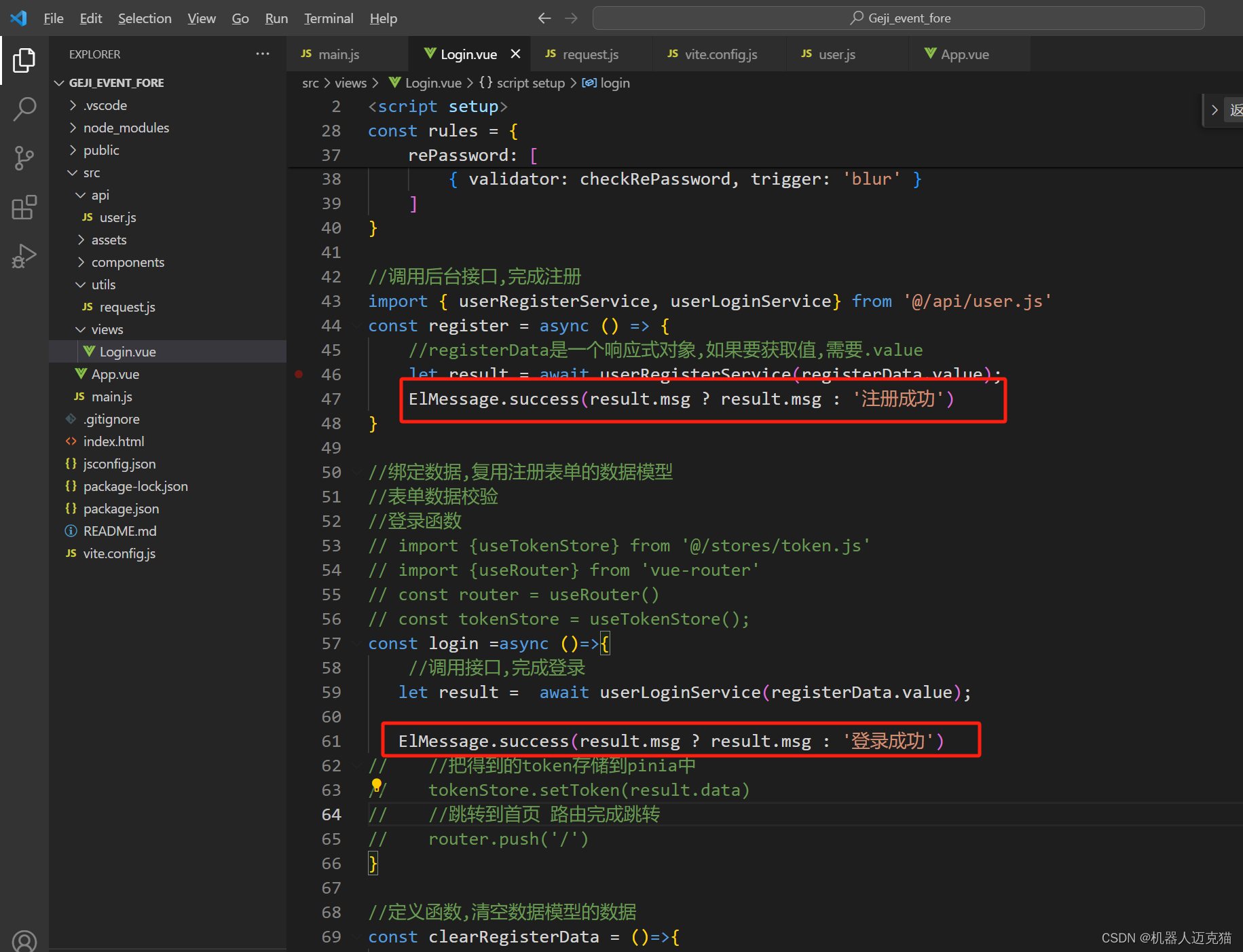
Spring Boot 笔记 024 登录页面
1.1 登录接口 //导入request.js请求工具 import request from /utils/request.js//提供调用注册接口的函数 export const userRegisterService (registerData)>{//借助于UrlSearchParams完成传递const params new URLSearchParams()for(let key in registerData){params.a…...

09_Java集合
一、Java集合框架概述 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态…...

HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-软件定时器
目录 一、软件定时器基本概念二、软件定时器运行机制三、软件定时器状态四、软件定时器模式五、软件定时器开发流程六、软件定时器使用说明七、软件定时器接口八、代码分析(待续...)坚持就有收获 一、软件定时器基本概念 软件定时器,是基于系…...
考研证件照可以自己用手机拍吗?考研证件照p过可以通过审核吗?考研证件照有什么要求
一、考研证件照可以自己用手机拍吗 现在的智能手机相机技术先进,大多都配备了高像素摄像头,使得自拍照片的质量有了大幅提升。相较于传统的证件照拍摄,使用手机自拍考研证件照理论上是可行的。然而,考研证件照需要满足一定的规定…...
win10 环境下Python 3.8按装fastapi paddlepaddle 进行图片文字识别1
###按装 用conda 创建python 3.8的环境,可参看本人python下的其它文章。 在pycharm开发环境下按装相关的模块: pip install -i https://pypi.tuna.tsinghua.edu.cn/simple fastapi pip install -i https://pypi.tuna.tsinghua.edu.cn/simple "uvi…...

json字符串的处理
json字符串的处理 【1】解析json字符串(1)如果json格式字符串 ,最外层 是 中括号,表示数组,就使用方法(2)如果json格式字符串,最外层是 大括号,表示对象,就是…...

Java基础String常见的编程练习
1.对字符串数组进行排序 package javalianxi;import java.util.Arrays; import java.util.Comparator;public class Test1 {public static void main(String[] args) {String[] array { "cd", "CD", "bc", "AB", "ab", &q…...
| 491.递增子序列 46.全排列 47.全排列 II)
代码随想录算法训练营(回溯5)| 491.递增子序列 46.全排列 47.全排列 II
491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 题目链接/文章讲解 视频讲解 46.全排列 本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用…...

专业140+总分420+南京信息工程大学811信号与系统考研经验南信大电子信息与通信工程,真题,大纲,参考书
今年顺利被南信大电子信息录取,初试420,专业811信号与系统140(Jenny老师辅导班上140很多,真是大佬云集),今年应该是南信大电子信息最卷的一年,复试线比往年提高了很多,录取平均分380…...

一元函数微分学【高数笔记】
1. 什么是微分?什么是微商? 2. 什么是函数的微分? 3. 在函数的微分中,有什么样的关系? 4. 一元函数的微分运用在什么题型中? 5. 什么是一元函数?...
(16)Hive——企业调优经验
前言 本篇文章主要整理hive-3.1.2版本的企业调优经验,有误请指出~ 一、性能评估和优化 1.1 Explain查询计划 使用explain命令可以分析查询计划,查看计划中的资源消耗情况,定位潜在的性能问题,并进行相应的优化。 explain执行计划…...
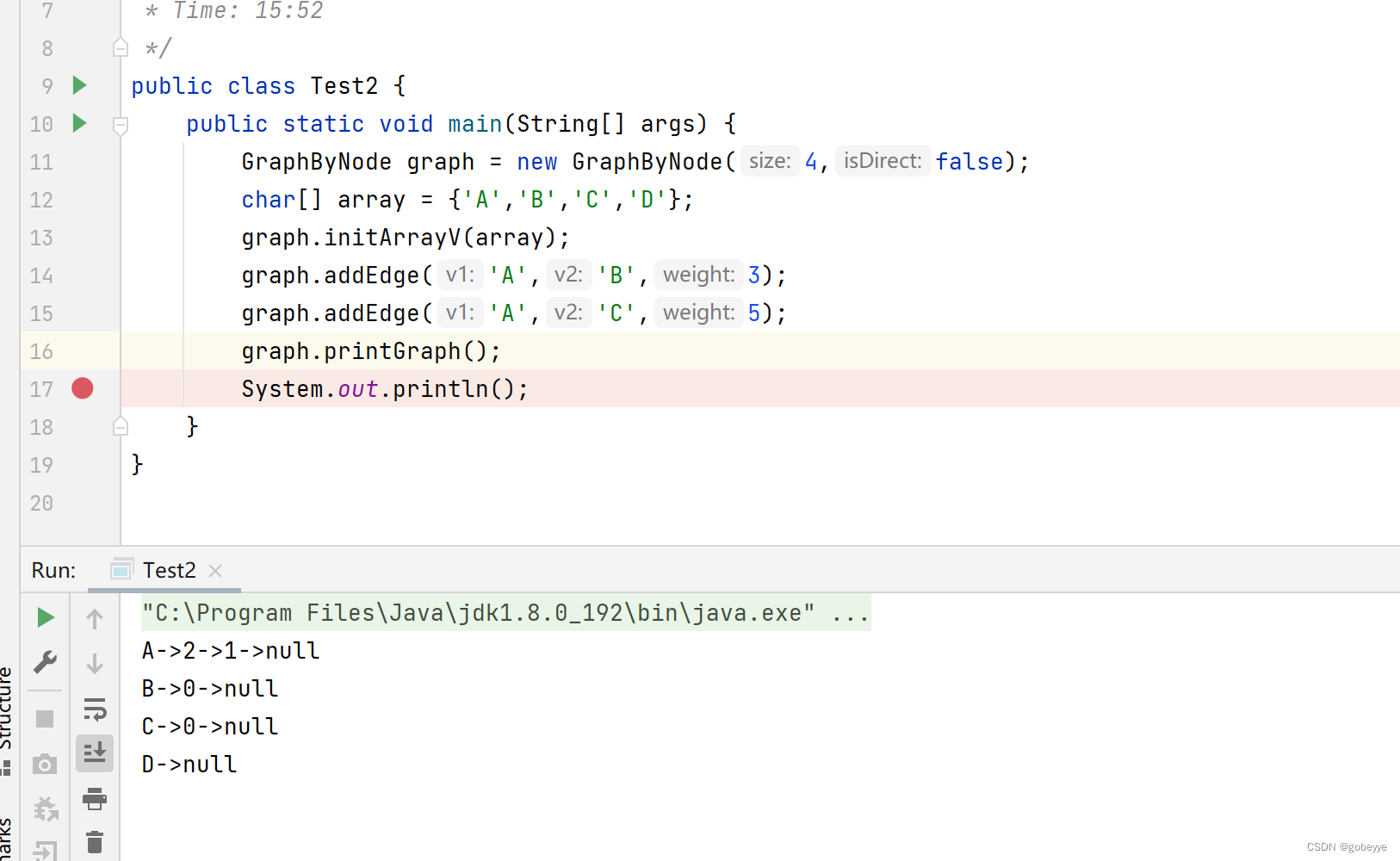
【详解】图的概念和存储结构(邻接矩阵,邻接表)
目录 图的基本概念: 图的存储结构 邻接矩阵(GraphByMatrix): 基本参数: 初始化: 获取顶点元素在其数组中的下标 : 添加边和权重: 获取顶点的度: 打印图…...

【AIGC】Stable Diffusion介绍
Stable Diffusion 是一个基于 OpenAI 的 Diffusion 模型的扩展版本,它采用了稳定扩散(Stable Diffusion)的技术,旨在提高图像生成和处理的质量。下面是 Stable Diffusion 的详细介绍: 基于 Diffusion 的图像生成&…...
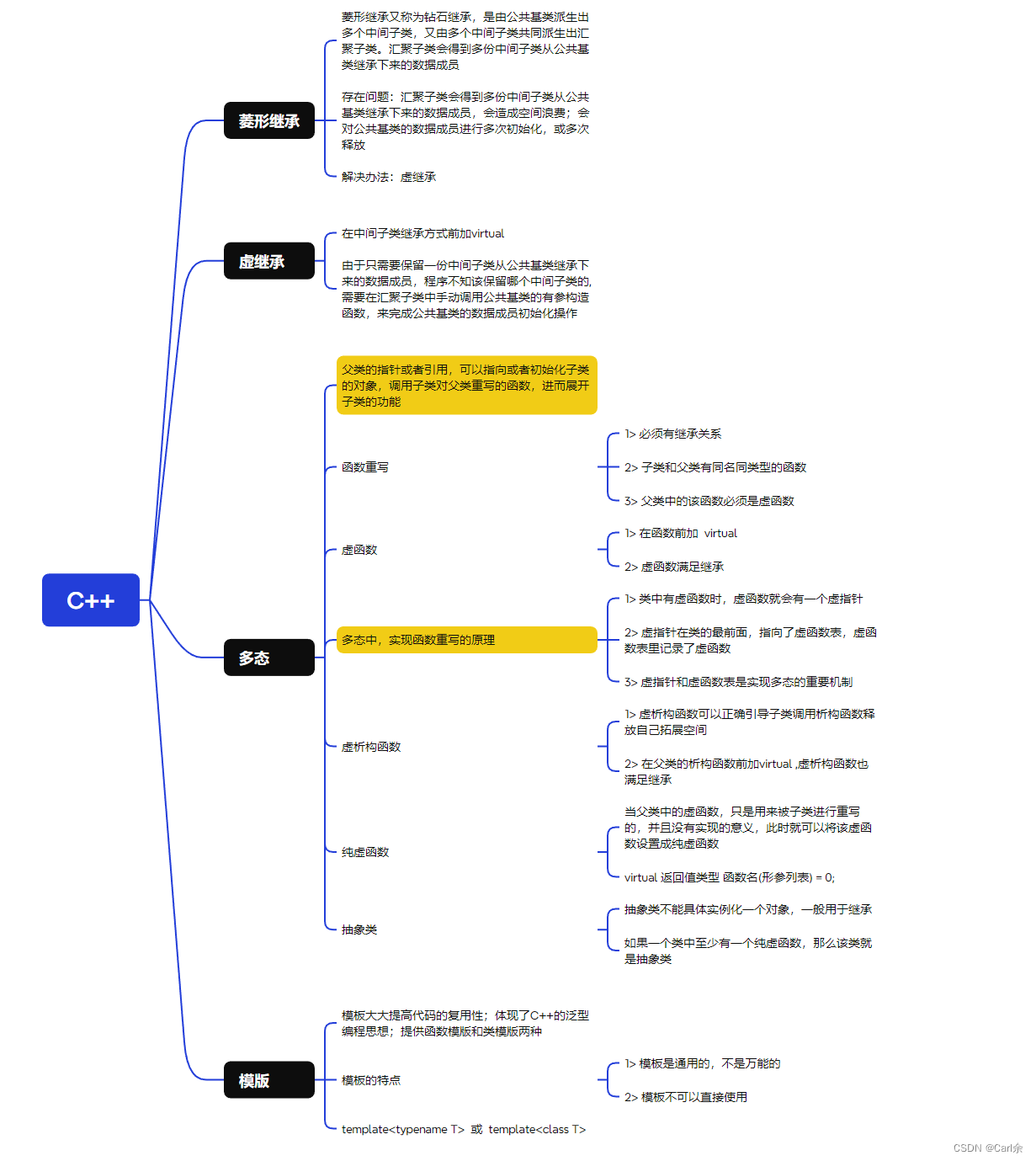
2024.2.18 C++QT 作业
思维导图 练习题 1>定义一个基类 Animal,其中有一个虛函数perform(),用于在子类中实现不同的表演行为。 #include <iostream>using namespace std;class Animal { public:virtual void perform() {cout << "这是一个动…...

【qt创建线程两种方式】
QT使用线程的两种方式 1.案例进度条 案例解析: 如图由组件一个进度条和三个按钮组成,当点击开始的时候进度条由0%到100%,点击暂停,进度条保持之前进度,再次点击暂停变为继续,点击停止按钮进度条停止。 案…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
